无诱导信息条件下基于信念学习博弈的车辆路径选择研究
2016-11-11刘世洁史国强
刘世洁,史国强
(重庆交通大学 交通运输学院,重庆 400074)
无诱导信息条件下基于信念学习博弈的车辆路径选择研究
刘世洁,史国强
(重庆交通大学 交通运输学院,重庆400074)
无诱导信息条件下,对驾驶员路径选择影响最大的是近期经验。本文以博弈论、信念学习理论为基础,建立γ-加权信念学习的无诱导信息车辆路径选择模型,通过matlab仿真得出不同初始状态下的博弈平衡结果。结果表明:当路网交通量小于路网通行能力时,经过多次选择博弈后路网会呈稳定平衡的状态,两条道路上的交通流趋向于均匀分布,路网交通流的分布与两条路径初始比例m无显著关系;当交通量大于等于路网通行能力时,路网会呈峰谷平衡的状态,路网交通量越大波动越明显,路网交通流的分布与两条路径初始比例m相关。
无诱导信息;路径选择;博弈论;信念学习
0 引 言
交通诱导的主要作用是将道路上的实时动态信息反馈给驾驶员,以便驾驶员合理选择行驶路线,它是智能交通(ITS)的一部分。马寿峰[1]在分析系统最优与用户最优各自特点的基础上,建立交通诱导中系统最优与用户最优的博弈协调模型。李振龙[2]应用演化博弈论建立诱导条件下驾驶员路径选择行为的演化模型,为制定交通诱导策略提供了理论支持。但经验丰富或对道路熟悉的驾驶员则不会接受诱导,而且在实际路网中,许多道路上并没有安装交通诱导系统。为此,有必要分析在无诱导信息条件下驾驶员路径选择情况。史国强[3]在无诱导信息条件下建立了基于有限理性模糊博弈的车辆路径选择模型。贺琳、周代平[4]以驾驶员的行程时间感受作为决策收益建立了基于累积自学习机制的无诱导信息条件下驾驶员路径选择博弈模型。刘建美[5]认为出行者在选择出行路径时,出行时间的长短是对其影响最大的指标。
传统的学者都是基于驾驶员为实质理性的模拟车辆路径选择过程,传统的模型只能描述处于均衡状态的个体及其驾驶行为,且缺少对参与驾驶员推理过程和能力的描述以及关于他们博弈情景知识的详细描述。本文通过借鉴经济学中人的选择行为,将驾驶员的路径选择行为信念模型化,利用博弈论建立γ-加权信念学习模型,尝试综合信念学习模型和虚拟博弈模型,分析在无诱导信息条件下车辆路径选择后路网的均衡状态。
1 模型建立
本文以驾驶员的感觉行程时间为路径所获得的收益。考虑如图所示的简单路网,A到B地有L1、L2两条路径,L1、L2的道路通行能力分别为C1、C2,C2表示驾驶员第k次通过L1、L2的实际交通量,路段行程时间函数ETA1,k、ETA2,k分别表示驾驶员第k次通过路径L1、L2到达B点的实际通行时间。
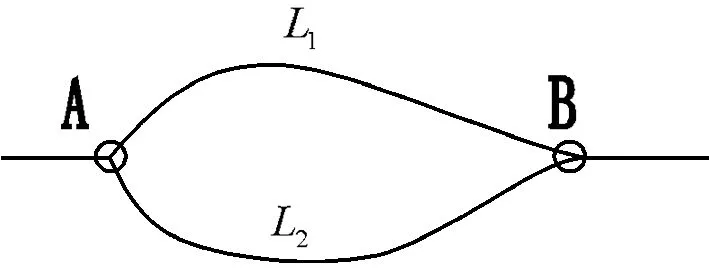
图1 路网示意图
(1)
式中:T0为自由行驶时(交通量为零)的路段行程时间;c为路段通行能力;q为路段实际交通量;∂、β为路段行程时间参数,一般取∂=0.15,β=4。
假设驾驶员每次都能记住自己以往经过每条路径的旅行时间,将驾驶员的经验累积作为路径择信念,其实质反映的是驾驶员赋予选择每条路径信念权重的比值。本文的γ-加权信念学习模型,就是人们基于博弈历史形成的信念,驾驶员i在第k+1次选择路径j的信念有下式给定:
(2)
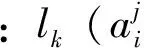
在无诱导信息条件下驾驶员只能根据自己的历史经验获取下一次的感觉行程时间。假设第k+1次的感觉行程时间表示为第k次的感觉时间和第k次实际行程时间的加权平均,未经历的路径感觉行程时间不变。第k次的实际行程时间所占的权重即为驾驶员第k+1次选择路径j的信念,那么第k次的感觉时间所占的权重为1减去驾驶员选择路径j的信念。驾驶员i第k+1次选择路径j的表达式为:

(3)
式中:ETgij(k)为驾驶员i第k次对路径j感觉行程时间;ETAij(k)为驾驶员i第k次经历路径j的实际行程时间;j=1,2;i=1,2……n;k=2,3……。
如果驾驶员i第k次选择了路径L1,那么驾驶员第k+1次出行前对路径L1、L2的感觉行程时间分别为:
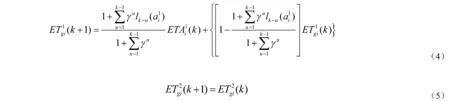
如果驾驶员i第k次选择了路径L2,那么驾驶员第k+1次出行前对路径L1、L2的感觉行程时间分别为:
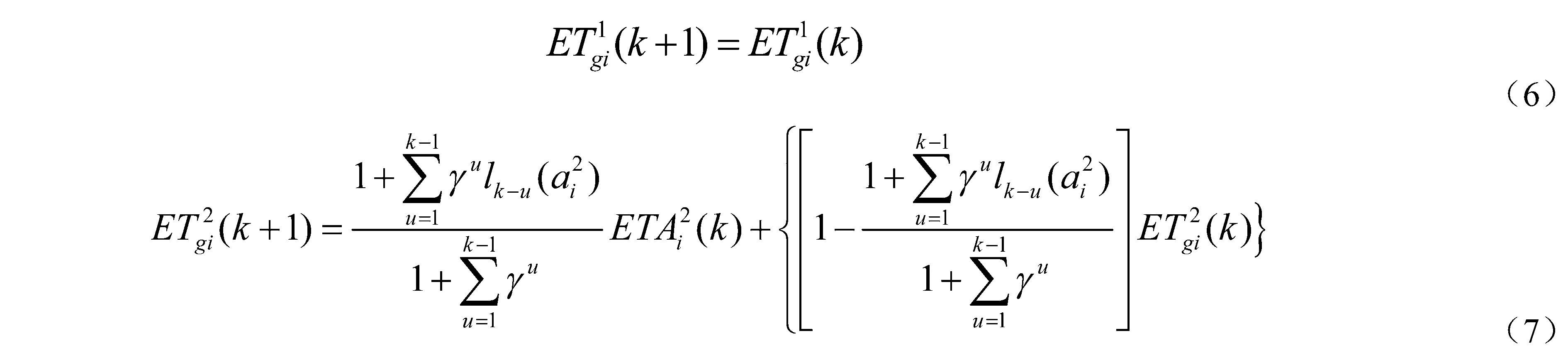
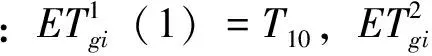
驾驶员根据感觉行程时间进行路径选择,本文利用logit模型确定在第k+1次出行时路径j的选择概率pjk+1为:
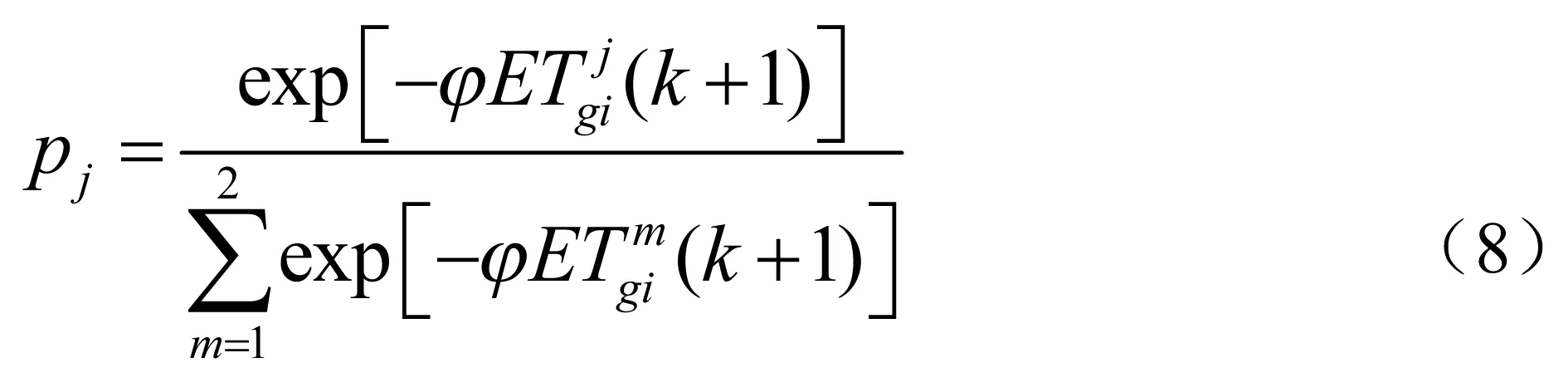
式中:j=1,2;pj为第k+1次出行时路径j的选择概率;ψ为与路径相关的参数,ψ表明出行者的理智程度ψ∈[0,+∞),当ψ→+∞时,驾驶员总是选择感觉行程时间较少的路径;当ψ=0时,驾驶员选择两条路径的概率总是相同的,都是1/2,而与感觉行程时间无关,本文取ψ=3。
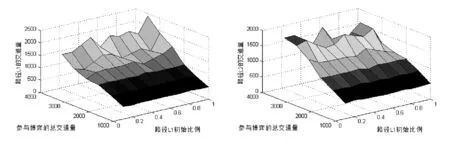
统计路网交通流时,在模拟中实现更新规则的步骤是:用随机数发生器产生0到1之间的随机数a,记p1(i,k+1)为驾驶员i第k+1次选择路径1的概率,1-p1(i,k+1)为驾驶员选择路径2的概率,若a Step 0:h=h+1,v=1,Δq=500,m=0.1,给C1、C2(C1≠C2)、T0、(m为初始状态路径L1车辆比例); Step 1:初始化,给出模型的初始状态,Q=q0,q1,0=m*Q,q2,0=Q-q1,0; Step 2:根据式(1)求得驾驶员第k次经过路径L1、L2的实际行程时间ETAi1(k)、ETAi2(k); Step 3:若驾驶员第k次经历路径L1,则分别根据式(4)、(5)求出ETgi1(k+1)、ETgi2(k+1)感觉形成时间; Step 4:若驾驶员第k次经历路径L2,则分别根据式(6)、(7)求出ETgi1(k+1)、ETgi2(k+1)感觉形成时间; Step 5:由第k+1次的感觉时间根据式(8)及改进的Learning Frequent规则确定第k+1次的路径选择; Step 6:sum(q1,k+1),sum(q2,k+1); Step 7:k=k+1,若k<2000,转Step2;否则,转Step8; Step 8:若m<1,Z(h,v)=q1,100,m=m+0.1,v=v+1转Step1,否则转Step8; Step 9:q0=q0+Δq,若q0<3000,转Step0,否则结束。 本算例中C1=1500,C2=1000,T10=30,T20=25,模拟仿真当交通量为定值,经2000次博弈选择过程后路径L1、L2上交通流的分布情况及其路径L1上的初始比例m从0.1依次递增到1时,路径L1、L2上交通流的分布情况: 图2 Q=1500路网交通流分布 图3 Q=3000路网交通流分布 交通量在两条道路的分布情况及博弈选择过程两条路径交通量的波动情况如下: 表1 交通量均值和方差 在无诱导信息条件下,当路网交通量小于路网通行能力时,经过多次选择博弈后路网会达到稳定平衡的状态;当路网交通量大于等于路网通行能力时,经过多次博弈选择后路网会呈现峰谷平衡的状态,两条道路上的交通量不能合理的分布在两条道路上,道路上交通流的波动性较大;当两条道路同时处于拥堵状态时(两条道路上的交通量均大于其通行能力),驾驶员更倾向选择较短的路径。 图4 不同Q、m下路径L1、L2的交通量 在无诱导信息条件下,当路网交通量小于路网通行能力时,路网交通流的分布与两条路径初始交通量的分布无显著关系;当路网交通量大于等于路网通行能力时,经过若干次博弈选择后路网会呈现峰谷平衡的状态,路网交通量的分布与两条路径初始交通量的分布相关。 本文以行为博弈论为基础,建立了γ-加权信念学习模型,并得出不同初始状态下的博弈平衡结果。无诱导的信念学习博弈演化过程反映了信念学习机制下,路网交通量小于道路通行能力时,无诱导也能够达到交通管理者所期望的良好状态;路网交通流的分布与两条路径初始交通量的分布无显著关系;当交通量大于等于路网通行能力时,路网交通量越大波动越明显。该模型在一定程度上反映了无诱导信息条件下,驾驶员的路径选择习惯,对诱导策略制定及其如何制定诱导策略有着一定的指导意义。 文章把驾驶员的感觉行程时间收益作为路径选择的唯一标准,今后的研究可以增加驾驶员的特性、道路状况等其他因素的研究,借以指导发布诱导信息。 [1]马寿峰,卜军峰,张安训.交通诱导中系统最优与用户最优的博弈协调[J].系统工程学报,2005,20(1):30-37. [2] 李振龙.诱导条件下驾驶员路径选择行为的演化博弈分析[J].交通运输系统工程与信息,2003,3(2):23-27. [3] 史国强,周代平,聂化东,等.无诱导信息条件下基于有限理性模糊博弈的车辆路径选择[J].山东交通学院学报,2015,23(2):31-35. [4] 贺琳,周代平.基于累积自学习机制的驾驶员路径选择博弈模型[J].交通运输研究,2015,1(4):49-55. [5] 刘建美.诱导条件下的路径选择行为及协调方法研究[D].天津:天津大学,2010.Study on Non-guidance Vehicle Routing Problem Based on Brief Learning Game LIU Shi-jie ,SHI Guo-qiang (Transportation & Traffic School,Chongqing Jiaotong University,Chongqing 400074,China) In the absence of guidance information conditions,the drivers usually rely on recent experience to choose the route. In this paper, based on the game theory and belief learning theory, the paper establishes a model of the no induced information vehicle routing model for the study of gamma weighted beliefs, and obtains the game equilibrium results under different initial states through MATLAB simulation. The results showed that the network traffic flow amount is less than the road network capacity, after repeated selection game posterior network will be a stable equilibrium state, two on the road traffic flow tends to uniform distribution, the distribution of network traffic flow and two initial path ratio m have no significant relationship; when the traffic flow is greater or equal to the road network capacity, the network will show the status of peak and valley balance, the larger the amount of network traffic flucations more obvious, the road network traffic flow distribution and two initial path ratio m have related. no induced information;routing choice; game theory; belief learning 2016-03-30 刘世洁(1992-),女,甘肃白银人,硕士,E-mail:847571661@qq.com。 U491 A doi:10.3969/j.issn.1671-234X.2016.02.010 1671-234X(2016)02-0045-042 求解算法
3 算例分析
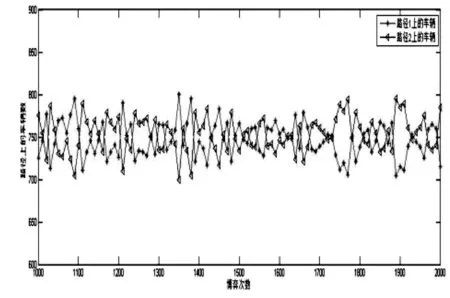
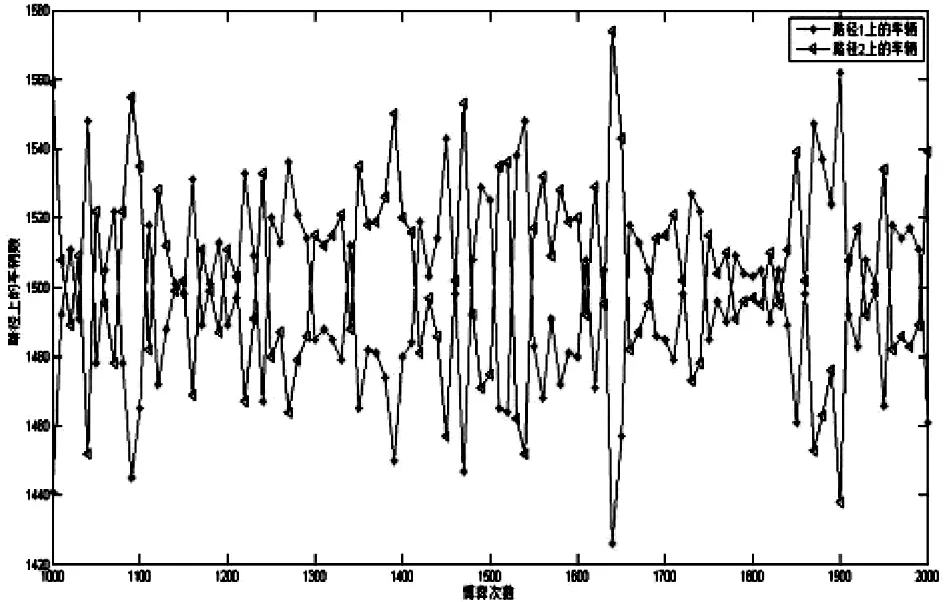

4 结 语
