N阶斐波那契数列和阶黄金分割及其应用

周　琪,池艳艳,周一勤

(1.温州市交通工程质量监督局,浙江 温州 325000；2.温州市交通重大项目前期工作办公室,浙江 温州 325000；3.温州市公路管理局,浙江 温州 325000)



N阶斐波那契数列和阶黄金分割及其应用

周琪1,池艳艳2,周一勤3

(1.温州市交通工程质量监督局,浙江 温州 325000；2.温州市交通重大项目前期工作办公室,浙江 温州 325000；3.温州市公路管理局,浙江 温州 325000)

黄金分割法是斐波那契数列的一个重要应用，具有优美的比例性、艺术性、和谐性，蕴藏着丰富的美学价值，揭示了自然界的一些科学规律。以广义的阶斐波那契数列推演出阶黄金分割，其中二阶黄金分割与混合料密级配填充理论在原理方面是相同的，以常用的水泥混凝土、水泥级配碎石和沥青混凝土混合料配合比的实例说明与二阶黄金分割吻合较好，以期通过二阶黄金分割原理找到水泥混凝土、水泥级配碎石和沥青混凝土混合料的最优配合比或通过黄金分割的方法快速或减少配合比试验次数，有效提高混合料结构的工程质量。

N阶斐波那契数列；黄金分割；混合料配合比

1　N阶斐波那契数列

著名的斐波那契数列[1]来自兔子繁殖的实际模型,具体数列：1,1,2,3,5,8,13,21,34,……，这一数列通项的递推公式为

F(m)=F(m-1)+F(m-2)

(1)

式(1)中，初始条件为F(0)=1，F(1)=1，m=2,3,4,…。

文献[2-3]将斐波那契数列递推公式推广为

Fn(m+n)=Fn(m+n-1)+Fn(m+n-2)+…+Fn(m),m=1,2,3,…

(2)

式(2)称为N阶斐波那契数列，式中初始条件为

Fn(0)=1，Fn(i)=2i-1，i=1,2,3,…，n-1,n=1,2,3…。

N阶斐波那契数列Fn(i),(i=1、2、3…、m,m≻n)，的通项公式为

(3)

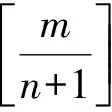
直接用式(3)求N阶斐波那契数列前项与后项的比值比较繁杂，现采用N阶斐波那契数列递推公式(2)直接进行导出，推导过程十分简洁。

当n=2时，二阶斐波那契数列前项与后项的比值由式(1)得

(4)

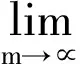
(5)

解一元二次方程式(5)，舍去负根得

(6)

这就是著名的黄金分割。

当n=3时，

(7)

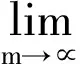
(8)

解一元三次方程式得其中一个正数根为φ3=0.543689012。

以此类推，当m→∝时，得

φn+φn2+φn3+…+φnn-1=0

(9)

式(9)就是N阶斐波那契数列前项与后项的比值通项公式。

(10)

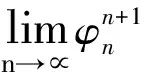
2　N阶黄金分割原理

2.1二阶黄金分割原理

图1　二阶黄金分割原理图

(11)

由式(11)得

(12)

解一元三次方程得

(13)

2.2N阶黄金分割原理

一般的线段AAn=L=1分割为n段(图2)，令

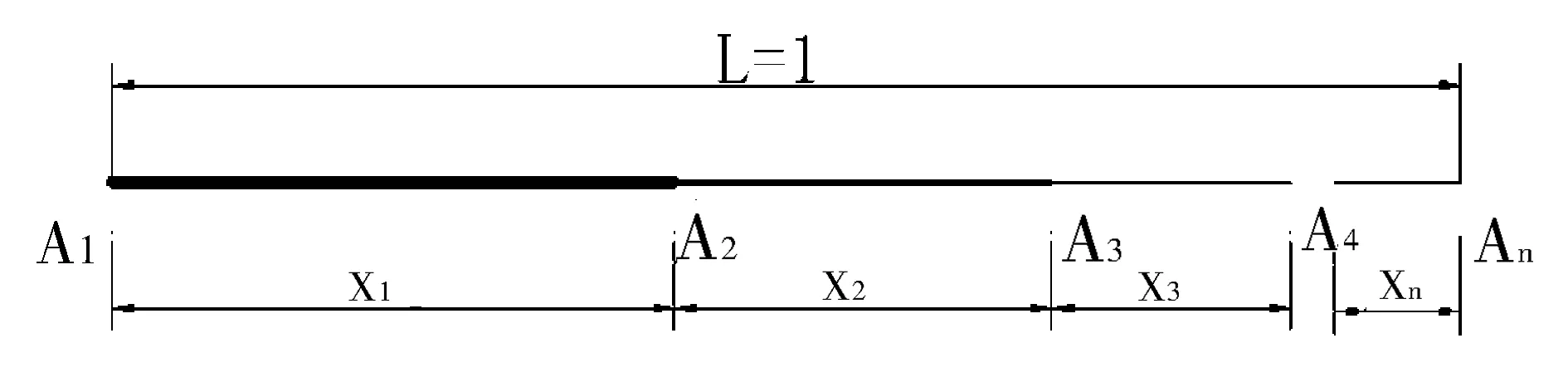
图2　N阶黄金分割原理图

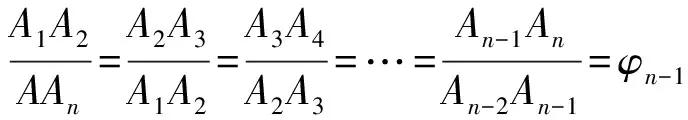
(14)

同理可得

(15)

这是一元n次方程。令x1=φn-1，则式(15)就是式(9)，这就是N阶黄金分割。

3　二重黄金分割原理的应用

黄金分割的应用领域十分广泛，许多文献作了介绍,特别在优选法中的应用更为著名[4]。

水泥混凝土、水泥级配碎石和沥青混凝土混合料都由多种不同粒径的松散集料如石子、砂逐级连续或间断(折断)级配相互之间嵌挤，并由石屑(矿粉)和水泥或沥青填充胶结材料形成稳固的结构。目前,常用的级配理论主要有最大密度曲线理论(如抛物线、i法、K法等)和粒子干涉理论或填充理论。本文以混合料密级配为例对二阶黄金分割进行探索。

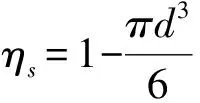
左—球形嵌挤模型　　右—集料嵌挤结构剖面

3.1水泥混凝土黄金分割配合比

水泥混凝土集料由水泥胶结后为密实固体，孔隙率几乎为零。选用文献[5]中碎石混凝土配合比表(中砂、5～40mm碎石)，分别配以普通水泥P.032.5、P.042.5、P.052.5等级进行数据分析，见表1。

由表1，按二阶黄金分割计算最大相对误差绝对值为6.6584%，可见二阶黄金分割与水泥混凝土配合比吻合较好；但从级配的比例绝对值来看，最大绝对误差为(0.295-0.28)=1.5%，这在实际工程中初步级配计算时可以接受的。对于C30～C50混凝土的其他组成原材料粒径范围也有基本相同的结果。

表1　文献[5]推荐的碎石混凝土配合比与二阶黄金分割统计分析表

3.2水泥级配碎石基层混合料

高速公路和一级公路按文献[6]C-B-1、C-B-2、C-B-3的水泥稳定级配碎石和老规范文献[7]的水泥稳定级配碎石配合比见表2。

由表2可见，文献[6]粗集料比例增加幅度较大，同时大幅度减少了细集料比例，按二阶黄金分割计算的石屑填充和胶结料最大相对误差为22.8%；老规范文献[7]与水泥碎石配合比中石屑填充和胶结料最大相对误差为-23.2%。新规范文献[6]针对老规范文献[7] 填充和胶结材料过多，在使用过程中容易出现开裂及抗冲刷能力不足的缺陷，增加了粗集料的含量、减少了填充和胶结材料。如将文献[6]、文献[7]推荐的水泥稳定级配碎石配合比进行平均，则与二重黄金分割吻合较好，相对误差大为减少，绝对误差仅为(29.5-26.0)%=3.5%。

3.3沥青混合料配合比

普通沥青及改性沥青密级配沥青混合料AC-25、AC-20、AC-16、AC-13等密级配沥青混合料[8]是按密级配原理设计组成的各种粒径颗粒的矿料与沥青结合料拌和而成，设计空隙率较小的嵌挤密级配沥青混凝土混合料。表3列出文献[8]推荐常用密级配沥青混凝土混合料配合比与二阶黄金分割方法统计分析情况。

由表3可见，各级集料配合比的平均值按二阶黄金分割计算最大绝对误差为(54.69-50.46)%=4.23%,最大相对误差为7.73%，总体与二阶黄金分割基本接近。

表2　文献[6]、文献[7]推荐的水泥稳定级配碎石配合比与二阶黄金分割统计分析表

注：①高速公路和一级公路基层碾压压实度标准为不小于98%，水泥级配碎石混合料压实成型空隙近似取2%，水泥用量取3～5%的平均值4%；②由于成型孔隙率和水泥用量是集料总量外加的，故表4中文献[6]的平均配合比和文献[7]推荐的配合比近似地除以1.06。

表3　文献[8]推荐的密级配沥青混凝土混合料配合比与二阶黄金分割统计分析表

注：由于沥青混凝土成型孔隙和沥青用量是集料总量外加的，故表3中粗集料：细集料：矿粉填充和胶结料占总重量平均配合比已近似地除以1.09。

4　结　语

(1)水泥混凝土、水泥级配碎石和集料密级配沥青混凝土混合料配合比原理与二阶斐波那契数列和二阶黄金分割式(11)在理论原理方面是相同的，其平均配合比符合二阶黄金分割原理。虽然现有的水泥混凝土、水泥级配碎石和集料密级配沥青混凝土混合料配合比实例与二重黄金分割存在着一定误差，但总体上吻合较好。这可能预示着运用二阶黄金分割原理可能找到水泥混凝土、水泥级配碎石和沥青混凝土混合料的最优配合比或通过0.618优选法的方法和途径快速或减少试验次数，有效提高混合料结构的质量。

(2)由于水泥混凝土、水泥级配碎石和沥青混凝土结构性能十分复杂，是由组成材料构造、性能、成型过程和使用条件等诸多因素决定的，阶斐波那契数列和阶黄金分割或二阶斐波那契数列和二阶黄金分割主要作用是体现这些混合料密级配嵌挤效果和功能，不能完全解决水泥混凝土、水泥级配碎石和沥青混凝土的物理、化学、力学和耐久性问题。通过二阶黄金分割原理，从最基础的混合料组成材料的几何特征入手，再运用材料学、化学和力学等多学科综合方法，优化和提高其结构强度、稳定性和耐久性。

(3)二阶黄金分割原理的应用方法、使用范围和实际效果有待于进一步的研究和实践的验证。

[1]吴松等．漫谈黄金分割[M]．乌鲁木齐：新疆科技卫生出版社，1994．

[2]孙振华．r阶Fibonacci数列[J]．银川师专学报：自然科学版，1993,25(3):40-45．

[3]梁昌洪，谭康伯，张伟．N代斐波那契数列和N代黄金分割[J]．西安电子科技大学学报:自然科学版, 2011，38(3):1-6．

[4]华罗庚．优选法平话及其补充[M]．北京：国防工业出版社，1971．

[5]杨绍林，田加才，田丽．新编混凝土配合比实用手册[M]．北京：中国建筑工业出版社，2002．

[6]JTG/T F20-2015，公路路面基层施工技术细则[S]．

[7]JTJ 034-2000，公路路面基层施工技术规范[S]．

[8]JTG F40-2004，公路沥青路面施工技术规范[S]．

N-Order Fibonacci Sequence and the N th-Order Golden Section and Its Application

ZHOU Qi1，CHI Yan-yan2，ZHOU Yi-qin3

(1.Wenzhou Traffic Quality Supervision Bureau，Wenzhou 325000,China;2.Wenzhou transportation major project preparatory work office，Wenzhou 325000,China;3. Wenzhou Highway Administration Bureau, Wenzhou 325000,China)

The golden section method is an important application of the Fibonacci sequence, with beautiful Proportional, artistry and harmony, contains rich aesthetic value, reveals the nature of the laws of science. To generalized N-order Fibonacci sequence to deduce the N th-order golden section, which second-order gold section and filling theory of mixtures dense gradation in terms of the principle is the same, to common combination ratio of cement concrete, cement gradation macadam and bituminous concrete mixture with specific examples and second-order gold section are in good agreement, with a view to the second-order gold section principle found the optimal ratio of cement concrete, cement gradation macadam and Bituminous concrete mixture or by golden section method for fast or reduced with than the number of trials and effectively improve the quality of the mixtures material structure engineering.

N-order Fibonacci Sequence；golden section；mixtures ratio

2016-05-04

周琪(1981-)，男，浙江温州人，高级工程师，工程硕士，E-mail：expway9@sina.com。

O15；U214.18

A doi：10.3969/j.issn.1671-234X.2016.02.006

1671-234X(2016)02-0024-05