哈汉双语班数学研究性学习案例探析

吴国梁

（晋江市第二中学，福建晋江362000）

哈汉双语班数学研究性学习案例探析

吴国梁

（晋江市第二中学，福建晋江362000）

以新疆哈汉双语班开展的数学研究性学习案例“哈萨克族毡房与组合几何体”“游牧民定居与统计分析”“天山天池与曲边梯形面积计算”等为素材进行实践研究，提出让学生感受生活体验，让学生体会深入探索，让学生感悟多元民族数学文化的思考和建议。

数学研究性学习；哈汉双语；实践研究

一、在哈汉双语班开展数学研究性学习背景

在新疆，双语教育一般是汉语言文字教学，加授少数民族语言文字。1999年，新疆就开设了双语教学实验班。笔者所支教的昌吉州四中2004年被自治区确定为区内少数民族双语教学示范学校，承担疆内高中班的教学任务。

2008年新疆启动普通高中课程改革，研究性学习作为普通高中新课程中综合实践课的组成部分，是每个学生的必修课程，三年共计l5学分。数学作为中学课程的主要学科之一，是学校开展研究性学习课程的主阵地。中学数学研究性学习是指学生在教师的指导下，从数学学科或生活实践中出现的问题中，明确研究课题，运用科学研究方法去获取知识，从而在掌握知识的同时，让学生了解、理解、掌握和应用数学学科的一种学习方法。

在哈汉双语班开展数学研究性学习，有利于推进学生学习方式的变革，培养学生的探究精神和创新能力；有利于对哈萨克民族资源的开发、利用，对民族文化开发的探讨；有利于培养学生爱家乡、爱祖国的情感以及社会责任感。

二、典型案例探析

【案例1】哈萨克族毡房与组合几何体

（1）数学情境：在新疆广袤无垠的草原上，点缀着朵朵白蘑菇似的毡房。毡房是游牧在草原或山间的牧民们流动着却很温馨的家，是一种易于拆装、携带方便的住房。它是哈萨克族传统游牧生活的结晶。

（2）研究的意义：毡房经过几千年的发展，凝聚着内涵丰富的民族文化，渗透着独特的生态技术因素。挖掘研究毡房的数学因素，对牧民定居的房屋设计提供借鉴，具有一定的现实意义。

（3）研究的方法。

①资料收集：通过查找网络、查阅图书、参观自治区博物馆等方式收集有关毡房的著作、期刊论文和相关资料。

②实地考察：深入奇台县江布拉克牧区考察，到乌昌南山牧区耐心访谈牧民，详细测量毡房样本的各项数据。

③分析研究：对搜集和考察所得来的资料进行分析归纳，分析其基本的几何结构体。分析哈萨克族毡房建筑构造特色，提出科学理论依据，为哈萨克族定居的房屋设计提供借鉴。

（4）提出问题

①观察哈萨克族毡房，你能看出它是由什么样的几何体构成吗？

②哈萨克族毡房的三视图是什么平面几何图形？

③如图测量数据，这个哈萨克族毡房的体积是多少？请说出你解决这些问题的计算方案。

④如图测量数据，这个哈萨克族毡房的表面积是多少？请说出你解决这些问题的计算方案。

（5）解决问题

①由下到上分别是由圆柱、球带、圆台、球冠组合而成；

②画出三视图（略）；

③圆柱V1=πR2h1，球带，圆台，球冠；

④圆柱M1=2πRh1，球带M2=2πR1h1，圆台M3=π（r3+r4），球冠。

问题3、4让学生深刻理22解定积分概念求出旋转体的侧面积、体积等，是对高中定积分和立体几何知识点的交汇应用，让学生体会到毡房的对称性、稳定性，是为求达到平衡、稳定的一种精确计算。这个设计艺术寓意着哈萨克族人民对和谐、对称等美的追求。

【案例2】游牧民定居与统计分析

（1）数学情境：新疆传统的游牧业生产主要依赖于天然草原，受自然条件的影响很大，具有不稳定性。其四季游牧的流动性，远离城镇的分散性，显著制约了牧民生产生活水平的提高。从2009年开始，新疆为改变畜牧业的落后生活条件，大力发展现代畜牧业，全面启动了游牧民定居工程。游牧民定居工程是新疆是实现稳疆兴疆、固边富民的具体体现。

（2）研究的意义：实施游牧民定居对于改善牧区生产生活条件，推进草原畜牧业的现代化进程具有重要的作用和意义。通过对新疆游牧民定居工程实施情况进行梳理分析，探讨了目前定居过程中的生态现象，有针对性地提出了对策建议。

（3）研究的方法。

①资料收集：通过查找网络、查阅图书收集整理牧民定居的政策文献、相关专著。到州农业局、畜牧局收集相关报表数据。

②实地考察：分别到昌吉市阿什里哈萨克乡努尔加村定居点，木垒哈萨克自治县大南沟乌孜别克族乡牧民定居点实地考察，住居体验，亲自感受牧区牧民的生存环境，走访当地居民。

③归纳分析：对经过实地调研所得来的资料进行归纳汇总、大数据分析，通过对生态环境、民族生活习俗等方面的研究，分析存在的主要问题，探讨对策，提出完善牧民定居体系建设的意见。

（4）提出问题

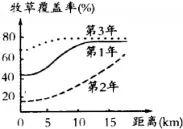
如图表示某草场以牧民的定居点为核心统计牧草覆盖率的变化情况，3年中的气候条件基本相同.分析该图你认为下列说法错误的是（）

A.放牧数量最大的是第2年，最少的是第3年

B.放牧数量与放牧范围呈正相关

C.第2年该草场的营养结构最复杂

D.定居放牧和轮牧相结合有利于提高载畜

（5）解决问题

分析：据图分析，牧草覆盖率最小的是第2年，最大的是第3年。生态系统中的组成成分越多，营养结构就越复杂，生态系统的自动调节能力就越强，其抵抗力稳定性就越强，相反的其恢复力稳定性就越弱。

解析：A.牧草覆盖率最小的是第2年，最大的是第3年，则放牧数量最大是第2年，最少的是第3年，故A正确；B.横坐标为距离，代表放牧范围，说明放牧数量与放牧范围呈正相关，故B正确；C.第2年牧草覆盖率最小，则营养结构最简单，故C错误；D.定居放牧和轮牧相结合，则牧草覆盖率能维持在较高水平，有利于提高载畜量，故D正确。

游牧民定居是一个长期、复杂的再社会化过程，需不断完善牧民定居体系建设，促进新疆草原畜牧业的现代化发展，提高牧民生活水平。

【案例3】天山天池与曲边梯形面积计算

（1）数学情境：天山天池古称“瑶池”，地处天山博格达峰北侧，位于新疆昌吉州阜康市境内，湖面海拔1900多米，南北长3.5公里，东西宽0.8～1.5公里，总面积380.69平方公里，最深处103米。由天池流出的三工河为阜康市农牧业主要灌溉水源。

在笔者援助支教的学校校园可远眺博格达峰，有几位学生家住天山天池周边，天山天池是他们再熟悉不过的景观之一。

（2）研究的意义：天山天池与曲边梯形面积计算是挖掘天山北坡数学因素之一。开展对天山天池的研究性学习，引导学生探究身边的数学，增强对天山天池生态保护的意识。

（3）研究的方法

①资料收集：通过查找网络、查阅图书等方式收集有关天山天池的著作、相关资料。

②实地考察：与农业局、林业局等专业人员对天山天池的地形地质进行详细勘探测量。走访天山天池管委会积累丰富的数据素材。

③分析研究：对调研所得来的资料进行分析，通过对地形地貌、生态环境等方面的研究，提出解决了天池地质灾难综合防治和发展生态游等综合方案。

（4）提出问题：呈现了一组图片—天山天池美景，提出了一个问题——如何计算天池的面积？

（5）解决问题：从天池美景开始，借助课件，让学生学会用分割、近似代替、求和、取极限四个步骤具体化求解曲边梯形的面积，体会“以直代曲”“无限逼近”的数学思想方法。在开展研究性学习的过程中，学生还以此为引子，研读《海岸线的长度问题》，从初等数学到高等数学逐步展开。

三、实施的思考与建议

1.让学生感受精彩源自生活的体验

生活是数学的源泉，数学是生活的提炼。汉斯·弗赖登塔尔认为：“数学来源于现实，存在于现实，并且应用于现实，数学过程应该是帮助学生把现实问题转化为数学问题的过程。”

我们学习中所用情境都来自于学生所熟悉的生活，让学生经历数学化的过程，体现数学素材与学生生活经验之间的密切联系。选题从所处的天山，居住的毡房，身边的牧民定居等案例入手，教师适时启发、点拨、总结，让学生体会到生活中蕴含着诸多的数学思想。

选题和研究的方向应力求引导学生自觉地置身于现实生活的大环境中，关心身边的数学问题，了解社会，关心社会，形成健全的人格。

2.让学生体会精彩源自深入的探索

著名数学教育家G·玻利亚指出：“拿一个有意义又不复杂的题目，去帮助学生挖掘问题的各个方面，使得通过这道题，就好像通过一道门户，把学生引入一个完整的领域。”

研究性学习是将学生置身于一种主动探究的学习状态下，引导学生从被动接受性学习转向主动学习。教师应该让学生动脑去思、动口去说、动眼去看、动手去做，指导学生用科学的研究方法，通过自己或小组合作的方式，收集、分析和处理资料，来体验知识的发生发展过程，通过调查、讨论、分析等手段学会学习，从而提高分析问题、解决问题的能力。

在学习中培养发现意识与实践能力，在探索中形成实事求是的态度和科学求真的精神，逐步形成正确的世界观，从而激发学生学习数学的兴趣和信心。

3.让学生感悟多元的民族数学文化

新疆多民族生活中蕴藏着丰富的数学文化，它们主要表现在建筑、服饰、宗教等方面，不同的民族有各自文化特色的图案、符号，不同的民族有不同的数学文化特征。《普通高中数学课程标准》将“体现数学的文化价值”作为课程的基本理念之一。在民族地区开展数学研究性学习，既有利于学生在自己熟悉的文化生活背景中学习数学，又有利于原生态民族文化资源开发、利用。

教师带动和指导学生对原生态民族数学文化开展研究性学习，可以收集、挖掘与培育原生态民族数学文化资源，丰富数学文化研究素材，揭示民族数学文化内涵。在学生学习过程中，应充分利用这些独特的教学资源，激发学生的探索热情，关注学生的切实体验，领略民族数学文化，可以提高学生的文化素养和创新意识，使学生以平等、开放的眼光看待本民族与其他民族文化中的数学成果，实现多元文化观点下的数学教育目的。

［1］教育部.普通高中数学课程标准（实验）［M］.北京：人民教育出版社，2003.

［2］罗永超，等.苗侗数学文化与数学情境教学［M］.北京：民族出版社，2012.

［3］木尔扎别克·阿不力卡斯.哈萨克毡房及其几何体结构［J］.伊犁师范学院学报，2008（2）.

（责任编辑：王钦敏）