双包覆层局域共振声子晶体带隙特性研究

张佳龙，姚 宏，杜 军，赵静波，董亚科

(1.空军工程大学航空航天工程学院，西安 710038； 2.空军工程大学理学院，西安 710051)



双包覆层局域共振声子晶体带隙特性研究

张佳龙1，姚 宏2，杜 军1，赵静波2，董亚科1

(1.空军工程大学航空航天工程学院，西安 710038； 2.空军工程大学理学院，西安 710051)

从理论上提出了一种双包覆层局域共振声子晶体结构，结合有限元对该结构带隙产生的机理、影响因素以及隔声特性进行深入分析。结果表明：带隙上边界频率主要由双包覆层弹性模量大的材料决定；下边界频率主要由基体密度小的材料决定。该声子晶体在低频范围具有良好的隔声特性，为声子晶体的结构设计提供理论指导。

声子晶体； 局域共振； 带隙机理； 隔声特性

1 引 言

在日常环境中，噪声污染(低频噪声)不但影响人们的工作学习，而且对人体健康都存在很大的危害，因此逐渐被人们广泛关注。噪声以弹性波的形式在声子晶体中传播，受其内部周期性结构作用，禁止传播的频率范围称为带隙[1]。基于声子晶体抑制波传播机理，研究人员设计了很多声子晶体结构，以达到低频宽带的目的[2-5]，例如弯曲梁类，薄板类，以及梁板复合结构。在隔声减振处理做出了突破性的贡献[6,7]。

二十一世纪初，香港科技大学的刘正猷教授等首次提出了基于局域共振机理的三维声子晶体结构[8]，他们的团队把直径为1 cm铅球外面均匀包覆2.5 mm的橡胶散射体，嵌入到环氧树脂立方基体构成。实验结果表明：带隙频率远低于相同晶格尺寸的Bragg带隙，实现了“小尺寸控制大波长”。K. M. Ho、C. K. Cheng 等根据局域共振机理制造出局域共振声子晶体结构，获得了200～500 Hz的宽频带隙，带隙范围内的声衰减强度比预测大11 dB[9]。2010年，沈礼等基于弹性波机理，将局域共振声子晶体结构引入到汽车盘式制动装置中，通过实验可验证其在实际工程的可行性，结论为：该声子晶体结构可在2000～2500 Hz频率范围内，声压降低幅值最大可达25 dB，平均噪声可达13 dB以上[10]。2013年，西安交通大学张思文等提出了一种用于回收环境低频振动能量新型局域共振单元结构，能够在250 Hz以下拥有几十甚至更多的共振频率，最低频率可降至20 Hz[11]。2014年，张晶的硕士论文《薄膜声学超材料板力学特性研究》，提出有限三维结构薄膜结构，共振频率为75.8 Hz，具有良好的隔声效果[12]。2015年，黄佳等提出一种圆管型局域共振声子晶体三维结构[13]，通过分析包裹层材料对带隙特性的影响，进一步提出带隙设计方法，使其满足结构中对减振、隔振及降噪的需求，应用于工程实际。Chen等首次发现，薄膜类具有局域共振类声子晶体，具有良好声衰减特性，而且会产生带隙频率范围为50～1000 Hz[14]。最近十几年，Lai Y、Mei J等[15,16]基于局域共振机理设计了体和薄膜超材料，解决了低频降噪减振的控制问题。

本文提出了双包覆层局域共振声子晶体结构在第一带隙频率范围为400～560 Hz 具有良好的降噪效果，最大隔声量为115 dB,而传统的单包覆层局域共振单元结构在第一带隙频率范围420～550 Hz内，最大隔声量为95 dB。而且双包覆层结构在不同频段带隙振动模态能够相互的转化，在低频段带隙主要是基体的密度起主导因素，高频段带隙主要是正八边形框密度起主导因素，带隙的下边界频率由基体密度大的材料决定，而上边界由正八边形框密度小的材料决定，这种结构的设计具有“轻质，宽带，强衰减”特性，最大隔声量为115 dB。本文对该结构带隙机理、带隙宽度影响因素以及隔声特性进行了分析，为声子晶体的制备提供理论依据。

2 共振带隙机理

2.1 局域共振声子晶体模型

该声子晶体结构由局域共振单元组成，如图1(a)。图1(b)和(c)分别为局域共振单元和第一布里源区；局域共振单元是由A(铅芯体)、B(内包覆层)及C(外包覆层)及D(环氧树脂)组成，即内外双包覆层包裹铅球构成散射体，嵌入到环氧树脂基体中。对应的材料和尺寸如表1,2。

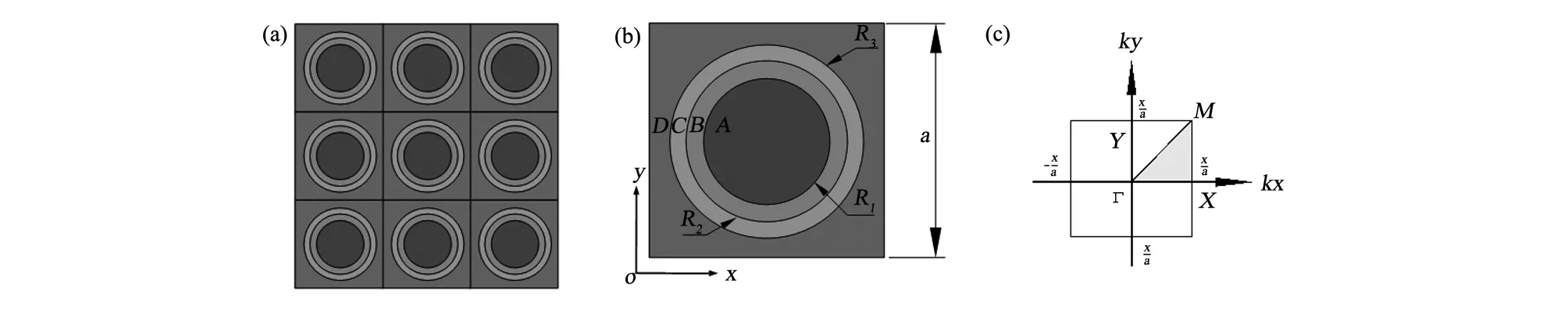
图1 (a)声子晶体结构；(b)单元结构简图；(c)第一布里渊区Fig.1 (a)The structure of phononic crystal;(b)unit structure drawing;(c)first brillouin zone

MaterialsDensityρ/kg·m-3Young'smodulusE/1010PaPoissonratio/μA(Pb)116004.080.369B(Siliconrubber)13001.175e-50.469C(Membrane)9802e-50.490D(Epoxyresin)39700.4350.370

表2 材料尺寸Tab.2 Structure sizes

2.2 局域共振带隙特性分析

根据局域共振单元结构的材料和尺寸参数，采用有限元法计算出该结构的能带图如图2。

图2 声子晶体能带图Fig.2 Band gap of phononic crystal

由图2可知，能带在点分开，这是由于长波行波在低频范围，其波长远远大于单元结构(晶格常数)的长度，弹性播在低频范围内传播与均匀介质相同，能带图呈线形关系。当基体中行波的频率接近或者等于共振单元固有频率时，则在单元体内会发生局域共振。基体中的长波将与该结构的共振模态相互耦合，绝大部分能量被局域在共振单元中，实现声屏蔽，因此会出现带隙，如上图阴影部分所示。该局域共振声子晶体在频率范围400～560 Hz和680～740 Hz，具有宽频带隙，为了进一步研究其产生带隙机理，选取第一布里源区的高对称点A、B、C、D、E和F的振动模态进行分析，图3为A-F振型图。

图3 A-F 振形图(黑色箭头表示了位移的相对大小和方向)Fig.3 Local resonance modes of structure(Black arrow indicates the relative size and directions)

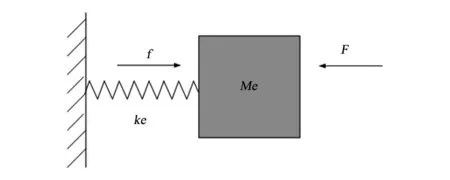
图4 等效“质量-弹簧”系统Fig.4 Equivalent “mass-spring” system

A和B点为平移共振模式，该单元结构在平移共振模式下动力学特性相同，此时局域共振单元：振子为环氧树脂，基体为由双包覆层包裹的铅球构成的散射体。橡胶带动散射体做横向或者纵向的平移运动，其中散射体一侧受挤压，另外一侧受到拉伸，并且为相邻振子之间以相同频率反向运动，相互抵消，保证基体框静止，内部相当于单自由系统，该共振单元结构可简化为“质量-弹簧”系统，如图4所示。共振带隙的固有频率，可根据单元结构简化“质量-弹簧”系统，并由其提供的等效质量和刚度来进行估算：

(1)

上式中，Me、ke分别代表振子等效质量，弹簧的等效刚度。

C和D点为扭转共振模式，对基体产生扭转作用，而没有对x、y方向有合力作用，基体中的长波很难与之发生相互耦合作用，因此不能产生共振带隙。

噪声以弹性波的形式传播到该结构单元时，会对基体产生力F作用，而振子Me运动会对基体产生一个反用力f，基体在两力共同作用下振动。当外激振力的频率与共振单元的固有频率接近时，两作用力反向叠加，基体合外力为零，因而基体趋于静止状态，弹性波被局域化，振动无法传播，仅限于共振单元中，能量被共振单元消耗掉，因此，此频段的弹性波不能继续传播。

E、F点平移共振模式，该结构的局域共振单元：振子为散射体，基体为环氧树脂。这就是传统的经典模型。该结构可等效弹性模量的“质量-弹簧”系统。弹性波传播到局域共振单元，会对共振单元产生力F作用，同时基体也会产生一个反作用力f，当弹性波的频率和此系统的固有频率接近时，元胞所受合外力为零，铅芯体趋于静止状态。该结构的简化模型由两个单自由度的“质量-弹簧”系统串联在一起，等效的弹簧的弹性模型模量减小。由根据公式(1)可知，等效的弹性模量减小，质量增加，该单自由系统固有频率减小。

由以上分析可知，处于E、F点平移共振模式的共振频率相比A、B点的较小，因此该局域共振声子晶体能带的上边界频率由前一个单自由系统中弹性模量大的决定，下边界频率由后一个单自由系统的振子(基体)密度小的决定。

3 影响带隙宽度的因素及隔声特性

3.1 带隙宽度的影响因素

为了进一步分析该结构带隙宽度和材料参数之间的关系，改变结构中铅芯体的密度，包覆层、基体的弹性模量，观察其带隙的变化，如图5所示。

图5 带隙宽度的影响因素(a)芯体铅密度；(b)内包覆层弹性模量；(c)外包覆层弹性模量；(d)基体材料密度Fig.5 Width of band gap affect factors(a)the core of Pb of material density;(b)the inner cladding layer of elastic modulus；(c)the outer cladding layer of elastic modulus;(d)the based material of material density

从图5可以看出，随着铅芯体的密度的增大，带隙的上、下边界频率均随之减小，但下边界频率变化率较快，较上边界频率降低至264 Hz，而且带隙的宽度也随着增大，这是由于简化为“质量-弹簧”系统中密度(即质量)增大，固有频率减小。根据公式(1)可知，振子密度增大，整个数值将减小，即该局域共振单元固有频率减小。由图(b)和(c)可知，随着双包覆层的弹性模量的增大，带隙的上、下边界的频率均增大，且带隙的宽度也随之增大，但带隙上边界的频率增大的程度较大，随后基本保持不变，这是由于简化模型中弹性模量增大，但弹簧的弹性模量在一定范围呈线性，超过临界值呈非线性，因此固有频率减小。由图5(d)可知，随着基体的密度的增大，带隙的上、下边界的频率均减小，但带隙下边界的频率减小的程度较大，这是由于局域共振单元中环氧树脂作为振子，基体为散射体的简化为模型中，基体密度增大，故带隙的固有频率减小。

根据以上分析可知，带隙上边界频率由包覆层的弹性模量大的决定，下边界频率由基体密度大的决定。

3.2 隔声特性

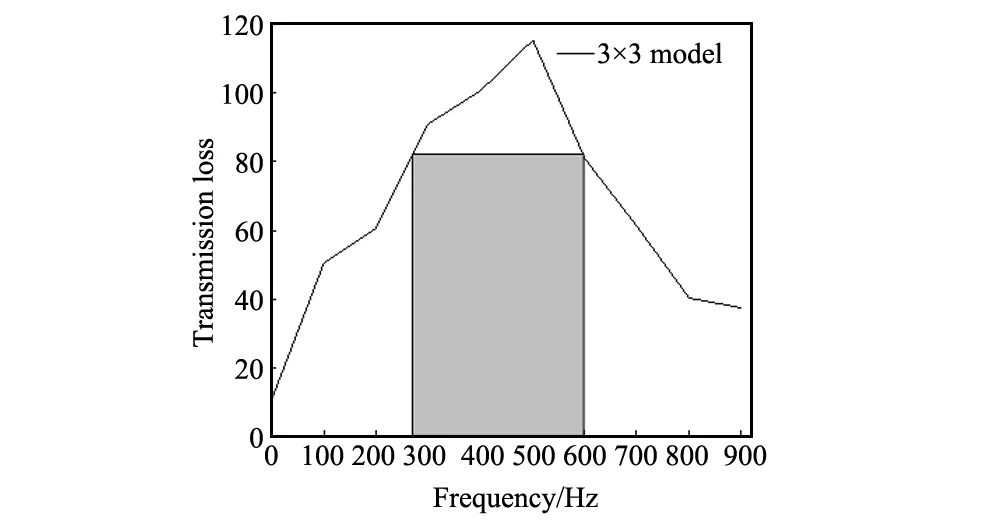
图6 声子晶体隔声量Fig.6 Sound insulation of the phononic crystal

为了进一步研究该结构的隔声特性，结合表1、2的材料参数和尺寸参数，计算3X3结构的隔声量如图6 所示。从图6可知，在频率范围400～560 Hz，该结构的隔声效果最好，最大隔声量为115 dB。根据式(1)可得，第一共振频率减小，能量衰减快，隔声量大，因此，声衰减特性增强。在低频段0～310 Hz，隔声量呈现先缓慢增大趋势；在高频段310～910 Hz，隔声量呈现先增大后减小趋势，主要由于简化模型中，等效质量减小，等效的弹簧刚度增强，局域共振系统能量损耗增大，隔声量增强；当系统等效质量达到极限时，系统就会失去局域共振特性，因此该结构优于传统的单包覆层局域共振单元结构。同时也验证了在此频率范围内正好为禁带，与能带结构吻合。

4 结 论

(1)本文提出一种双包覆层局域共振声子晶体结构模型，采用有限元法对结构的带隙生成机理，隔声特性进行深入分析，该结构在中低频段(400～560 Hz)具有良好的隔声特性，而且带隙边界频率等效两个单自由度的“质量-弹簧”系统，该局域共振单元结构没有严格意义上的基体和振子之分，他们之间可以相互转化；

(2)带隙是由基体行波与局域共振单元相互耦合作用的结果，通过改变结构性能参数(芯体密度，包覆层、基体的弹性模量)，可以调节带隙宽度及带隙上下边界频率；带隙上边界频率由包覆层弹性模量大的决定，下边界频率由基体密度大的决定，从而确定影响带隙宽度，隔声量的关键因素，从而达到优化结构目的。

这种结构的设计为制备“低频，宽带，强衰减”特性的声子晶体提供了理论依据和方法指导。

[1] 温熙森，温激鸿，王 刚，等.声子晶体[M].北京：国防工业出版社，2009.

[2] Kushwaha M S，Halevi P，Dobrzynski L,et al.Acoustic band structure of periodic elastic composites[J]．Phy.Rev.Lett.,1933,71(13):2022-2025.

[3] Li Y G,Chen T N,Wang X P,et al.Band structures in two-dimensional phononic crystals with periodic Jerusalem cross slot [J].PhysicaB,2015,456:261-266.

[4] Yu K P,Chen T N,Wang X P.Large band gaps in phononic crystal slabs with rectangular cylinder inclusions parallel to the slab surfaces[J].JournalofPhysicsandChemistryofSolids,2013,74:1146-1151.

[5] Wang Y L,Song W,Sun E W,el at.Tunable passband in one-dimensional phononic crystal containing a piezoelectric 0.62Pb(Mg1/3Nb2/3)O3-0.38PbTiO3single crystal defect layer[J].Physica.E.2014,60:37-41.

[6] 温激鸿，温熙森.声子晶体振动带隙及减振特性研究[D].长沙：国防科技大学学位论文，2005.

[7] 郁殿龙，邱 静.基于声子晶体理论的梁板类周期结构振动带隙特性研究[D].长沙:国防科学技术大学学位论文,2006.

[8] Liu Z,Zhang X,Mao Y,et al.Locally resonant sonic materials[J].Science,289:1734-2000.

[9] Ho K M,Cheng C K,Yang Z,et al.Broadband locally resonant sonic shields[J].Appl.Phys.Lett.,2003,83(26):5566-5568.

[10] 沈 礼，吴九汇，陈花玲，等.声子晶体结构在汽车制动降噪中的理论研究及应用[J].应用力学学报，2010，27(2):0293-0295.

[11] 张思文，吴九汇.基于局域共振声子晶体结构的低频振动能量回收研究[J]．固体力学学报，2013，34(4)：333-341.

[12] 张 晶，谢志民.薄膜声学超材料板的力学特性研究[D].哈尔滨: 哈尔滨工业大学学位论文，2014.

[13] 黄 佳，尹 进，张 昭，等.圆管型局域共振声子晶体三维构型振动带隙研究[J].计算力学学报，2015，32(3)：0353-0356.

[14] Chen X,Xu X C,Ai S G,et al.Active acoustic metamaterials with tunable effective mass density by gradient magnetic fields[J].J.Appl.Phys，2014，105：071913-071922.

[15] Lai Y,Wu Y,Sheng P,et al.Hybrid elastic solids[J].NatureMaterials,2011,10(8)：620-624.

[16] Mei J,Ma G,Yang M,et al.Dark acoustic metamaterials as super absorbers for low-frequency sound[J].Nat.Commun.,2012,3(3)：756-762.

Band Gap Characteristics of Periodic the Double Cladding Layer Locally Resonant Phononic Crystal

ZHANGJia-long1,YAOHong2,DUJun1,ZHAOJing-bo2,DONGYa-ke1

(1.College of Aeronautics and Astronautics Engineering,Air Force Engineering University,Xi’an 710038,China；2.College of Science,Air Force Engineering University,Xi’an 710051,China)

The double cladding layer local resonance mechanism resonators in phononic crystal was proposed. The band gap formation mechanisms, the width of band gap affect factors, and sound insulation quantities with finite element methods were analyzed. These results show that starting frequency depends on higher elastic modulus of the double cladding layer elasticity, cut-off frequency depends on smaller bulk density of elasticity. These results that phononic crystal has a good the light quality, low-frequency, width band gap and the sound insulation of characteristics, provides potential applications prospect the reducing of low-frequency noise in the mechanical equipments and provides theoretical guidance for the design of the structure of the phonon crystal.

phononic crystal;local resonance;band-gap mechanism;sound insulation of characteristic

国家自然科学基金(11447147,11504429);陕西省自然科学基础研究计划(2015JQ5155)

张佳龙(1990-)，男，硕士研究生.主要从事声子晶体振动与降噪方向的研究.

姚 宏，博导，教授.

O734

A

1001-1625(2016)09-2767-05