基于概率与小波分析的故障检测方法及其应用
2016-11-10赵佳佳马喜平贾嵘沈渭程党建
赵佳佳,马喜平,贾嵘,沈渭程,党建
(1.西安理工大学水利水电学院,陕西西安 710048;2.国网甘肃省电力公司电力科学研究院,甘肃兰州 730050)
基于概率与小波分析的故障检测方法及其应用
赵佳佳1,马喜平2,贾嵘1,沈渭程2,党建1
(1.西安理工大学水利水电学院,陕西西安710048;2.国网甘肃省电力公司电力科学研究院,甘肃兰州730050)
针对小波阈值法无法准确从强噪声中检测到故障信号的问题,提出了一种基于概率与小波分析的故障检测方法。首先基于分位数的定义将各分解层的小波系数进行分割,利用各层的若干个分界值计算信号各个位置发生故障的概率,再结合小波阈值分析,得出最终的检测结果。通过仿真和实测分析,表明该方法可以准确、有效地检测到故障信号,具有良好的应用价值。
故障检测;概率;分位数;小波分析
电气设备故障不仅会影响电力系统的正常运行,还会危及其他设备及人员的安全,因此必须对其运行状况进行状态监测与故障诊断。但由于实际采集到的信号通常会包含大量噪声干扰,这使得早期及微弱故障故号难以被准确识别,因此必须采取有效措施对噪声进行抑制[1-2]。小波分析在时频域上均具有良好的分析特性,非常适用于处理非线性、非平稳信号,因而在信号检测中受到了广泛应用[3]。目前基于小波理论的分析方法包括:1)模极大值法;2)阈值法;3)空域相关法。其中阈值法[4]应用最为广泛,主要包括3个关键步骤:1)选择合适的小波基;2)确定最佳的分解层数;3)设置一定的阈值。阈值法通常都是通过单一的阈值对各层的小波系数进行处理,若阈值选取过高,可能无法检测到幅值较小的故障信号,引起漏检;反之,若阈值选取过低,则检测到的可能为噪声,造成误检。
为此,本文在小波分析中加入了概率[5]的计算,提供了一个用于表征信号各处发生故障的可能性大小的概率值,并将此计算结果与经阈值处理的重构信号相结合,综合进行判断,以实现故障信号的准确检测。
1 分界值的确定
传统的数据分类,是根据幅值的大小与固定间隔来进行,并未考虑到信号本身的分布特性,因此具有一定的局限性。分位数则是根据数据出现的概率进行分类。在实际中,故障信号的发生时间及幅值大小均是未知的,因此根据分位数对数据进行分类更为贴切。图1为采用不同的方法对数据进行分类的结果。

图1 不同方法的分类结果Fig.1 Classification based on different methods
图1中蓝色圆圈代表按照绝对值大小进行排序的数据点,每一条红色实线代表一个用于数据分割的边界值。本文首先在各分解层设置一个基准值,再根据分位数的定义逐步确定多个分界值,进而提供一个概率值用于判断各处发生故障的可能性。首先将所有数据按大小进行排列,若计算所得基准值所处位置位于该数列的1%,则认为该数列的第1%个数即为第一个分界值,若要设置5个分界值,则每个分界值的位置间隔为0.2%,第二个分界值所处位置为第0.8%,以此类推,得到5个用于概率计算的分界值。各层分界值的个数根据信号特性及长度等来选择,个数越多,检测效果越精确,但是相应的计算量也会增大。本文中各层分界值的个数均设为10。
2 基于概率与小波分析的故障诊断方法
2.1概率的计算过程
研究表明,经过小波变换后,信号对应的小波系数几乎会出现在所有分解层上,且其突变点在各个分解层的同一位置都会出现较大的峰值。而噪声通常却并不具备该特性。因此,本文引入概率的计算,用以表征原始信号各处发生故障的可能性大小。
计算概率时,首先要选定一个小波基和分解层数,然后按以下步骤进行计算:
1)将各层小波系数的模值按从大到小的顺序进行排列。
2)计算基准值所处位置,计算公式如下:

式中:Mea(dj)、Max(dj)分别为经过第j个分解层上所有小波系数模值的平均值与最大值。
3)确定分界值的个数,计算其余分界值所处位置。
4)根据分位数的定义计算各个位置所对应的分界值。
5)根据分界值计算信号各处发生故障的概率,即
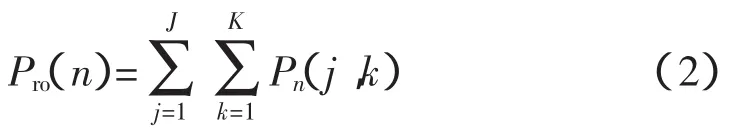
式中:Pro(n)为原始信号中第n个位置产生故障的概率值;J为小波的最大分解层数;N为各个分解层上的分界值的个数;Pn(j,k)为n点的局部“概率”,若该点小波系数的模值小于第k个分界值,其值取0,反之,其值取1。
2.2基于概率与小波分析的方法
本文将概率与小波阈值法相结合,其具体实现过程如下:
1)选取最优的小波基与最佳的分解层数,对原始信号进行分解。
2)将各层的小波系数进行存储。
3)在各层设置一定的阈值,对存储的小波系数作处理,并利用最终的小波系数进行信号的重构。
4)按照本文提出的概率计算步骤,根据存储的小波系数计算信号各个位置的概率值。
5)将重构信号与概率值进行对比分析,综合判断各处是否发生故障。
利用本文方法作信号处理时,首先要选取合适的小波基。Daubechies(db)小波具有很好的紧支性和正交性,并且为双正交函数[6-8],因此常被用作故障信号的分析与处理。
其次就是确定最佳的分解层数。信号对应的小波系数的特点为:数量少、幅值大,而噪声所对应的小波系数则相反,即数量多且幅值小,且多分布在较低的分解层。根据这一特性,可利用白化检验[7]确定最终的层数。
小波分析中阈值的选取有多种方式。本文采用下式确定阈值[8]:

式中:Med(dj)为第j个分解层上所有小波系数模值的中值;L(dj)为第j个分解层上的小波系数的数目,j= 1,2,…,J。
3 仿真与实测信号分析
3.1仿真信号分析
本文以局部放电(Partial Discharge,PD)信号为例,进行相关分析。分别选取以下2种模型来表示局放脉冲[4]:1)单指数衰减振荡函数;2)双指数衰减振荡函数。PD信号波形如图2所示。给局放信号中加入白噪声进行研究,白噪声波形如图3所示。得到的混合信号如图4所示,其信噪比为0.5 dB。
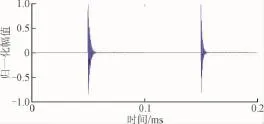
图2 PD信号Fig.2 Partial discharge signal
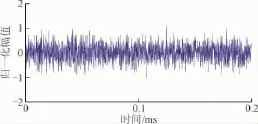
图3 白噪声Fig.3 White noise
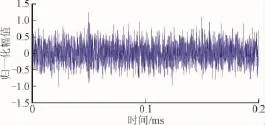
图4 混合信号Fig.4 The mixed signal
3.2仿真结果及分析
根据上述分析,本文选用的是db4小波,分解层数确定为6层。处理结果如图5所示。
由图5(a)可知,阈值法检测到了3个故障信号。而图5(b)中很明显只有两处的概率值较大。由此可以判定,第一处应为幅值较大的噪声信号,而后面两个概率较大的位置所对应的才是真实的故障信号。经过分析比较,这一结果与实际情况相符,从而避免了信号的误检,实现了故障的有效检测。
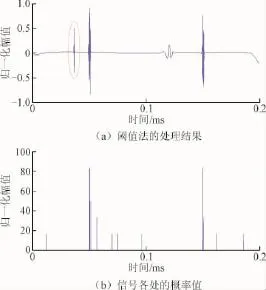
图5 检测结果Fig.5 The detection results
3.3实测信号分析
图6所示为从某发电厂的局部放电监测系统中得到的现场信号,选取了2 000个采样点。根据上述分析,选取db8小波,分解层数同为6层。处理结果如图7所示。

图6 实测信号Fig.6 The measured signal

图7 检测结果Fig.7 The detection results
由图7(a)可以看出,阈值法只检测到一个故障信号。但在图7(b)中,有2处所对应的概率值较大。将二者的结果进行结合,可得到实测信号中有2处发生故障,从而避免了信号的漏检。
4 结语
针对淹没在强噪声中的故障信号,提出了一种基于概率与小波分析的故障检测方法。在小波阈值处理中加入了概率计算,解决了仅基于单一阈值进行数据处理的缺陷,并且避免了故障的“误检”或“漏检”。通过MATLAB对仿真及实测信号分别进行分析处理,结果表明该方法能够准确可靠地检测到故障信号,具有一定的实用性。
[1]刘军,宋新甫,肖波.基于独立分量分析的发电机局部放电信号提取[J].电网与清洁能源,2008,24(12):61-64.LIU Jun,SONG Xinfu,Xiao Bo.Extracting partial discharge signals of generator based on independent component analysis[J].Power System and Clean Energy,2008,24(12):61-64(in Chinese).
[2]程昌奎,郑永健,庞军,等.变压器局部放电监测中的最优小波与脉冲鉴别去噪方法研究[J].高压电器,2016,52(3):0123-0128.CHENG Changkui,ZHENG Yongjian,PANG Jun,et al.Extraction of partial discharge signals from noise based on scale wavelet selection and pulse-sequence analysis[J].High Voltage Engineering,2016,52(3):0123-0128(in Chinese).
[3]蒲会兰,丁世文,鲁怀伟,等.小波变换及其在信号去噪中的应用[J].现代电子技术,2012,35(19):52-55.PU Huilan,DING Shiwen,LU Huaiwei,et al.Wavelet transform and its application in signal denoising[J].Modern Electronics Technique,2012,35(19):52-55(in Chinese).
[4]艾比布勒·赛塔尔,徐文邦,王德平,等.局部放电小波阈值去噪算法的改进[J].电子测试,2014,1(10):26-28.Abby match Buller,XU Wenbang,WANG Deping,et al.The improvement of wavelet threshold denoising algorithm of partial discharge[J].Electronic Test,2014,1(10):26-28(in Chinese).
[5]Junhyuck Seo,Hui Ma,Tapan Saha.Probabilistic wavelet transform for partial discharge measurement of transformer[J].IEEE Transactions on Dielectrics and Electrical Insulation,2015,22(2):1106-1117.
[6]党存禄,张旭.基于Daubechies小波族的电能质量信号去噪方法研究[J].电网与清洁能源,2014,30(12):71-74.DANG Cunlu,ZHANG Xu.Power quality signal denoising based on Daubechies wavelet clan[J].Power System and Clean Energy,2014,30(12):71-74(in Chinese).
[7]张吉先,钟秋海,戴亚平.小波门限消噪法应用中分解层数及阈值的确定[J].中国电机工程学报,2004,24(2):118-122.ZHANG Jixian,ZHONG Qiuhai,DAI Yaping.The determination of the threshold and the decomposition order in threshold de-noising method based on wavelet transform[J].Proceedings of the CSEE,2004,24(2):118-122(in Chinese).
[8]LI Jian,JIANG Tianyan,Stanislaw Grzybowski,et al.Scale dependent wavelet selection for de-noising of partial discharge detection[J].IEEE Transactions on Dielectrics and Electrical Insulation Measurement,2010,17(6):1705-1714.
(编辑李沈)
A Fault Detection Method Based on Probability and Wavelet Analysis and Its Application
ZHAO Jiajia1,MA Xiping2,JIA Rong1,SHEN Weicheng2,DANG Jian1
(1.Xi'an University of Technology,Xi'an 710048,Shaanxi,China;2.Electric Power Research Institution,State Grid Gansu Electric Power Company,Lanzhou 730050,Gansu,China)
As the wavelet threshold method can not detect the fault signal from strong noises accurately,a fault detection method based on probability and wavelet analysis is proposed in this paper.Firstly the wavelet coefficients of each decomposition layer are divided on the basis of quantile.And the probability which indicates the possibility of fault of each position in the signal is calculated based on boundary values and the final detection result is obtained based on the result of wavelet threshold analysis.Simulation and experimental results show that this method is able to detect the fault signal accurately and effectively,and it has good application value.
fault detection;probability;quantile;wavelet analysis
1674-3814(2016)07-0092-04
TP27
A
国家自然科学基金项目(51279161)。
Project Supported by National Natural Science Foundation of China(NSFC)(51279161).
2015-12-08。
赵佳佳(1992—),女,硕士研究生,研究方向为高压电气设备绝缘在线监测及故障诊断。
