基于2n+1点估计法的含分布式电源配电网的电压质量概率评估
2016-11-10陈伟郭秋池裴喜平
陈伟,郭秋池,裴喜平
(兰州理工大学电气工程与信息工程学院,甘肃兰州 730050)
基于2n+1点估计法的含分布式电源配电网的电压质量概率评估
陈伟,郭秋池,裴喜平
(兰州理工大学电气工程与信息工程学院,甘肃兰州730050)
为准确评估分布式电源及负荷功率的随机特性对配电网电压质量的影响,在已有的点估计法的基础上,提出一种2n+1点估计法,求解分布式电源配电网概率潮流。该方法考虑了风速,光照强度以及负荷随机特性对配电网的影响,通过得到电压概率统计值,然后结合半不变量理论与Gram-Charlier级数展开得到相应的概率密度函数以及含分布式电源节点的电压越限概率,对含分布式电源的配电网电压质量进行概率评估。以含有分布式电源的IEEE-30节点系统作为算例,通过2n+1点估计法进行概率潮流计算,分析了分布式电源接入前后对系统节点电压的影响。
分布式电源;电压质量;概率潮流;2n+1点估计法;概率密度函数
随着化石能源日趋枯竭以及低碳经济发展的需要,能源问题在世界范围内备受关注和重视。在电力系统中,新能源和可再生能源的应用,促使利用可再生能源的分布式发电技术得到大力发展[1]。分布式电源具有小规模、分散、就近、灵活等特点,被大量接入电力系统配电网中。其中,以风力发电和光伏发电为代表的分布式电源最为突出。然而由于分布式电源出力具有随机性、间歇性、波动性和不可控性,发出的有功功率很难准确预测和控制[2-4],由此对用户及负荷侧带来了一系列电能质量问题,尤其表现在电压质量方面,从而使得电压质量评估变得更加复杂。
概率潮流(probabilistic load flow,PLF)能够计及电力系统中多种不确定性因素[5],如电网网络拓扑结构、发电机出力、电力设备的参数以及负荷功率等情况,同时还可以分析考虑由于分布式电源具有的物理特征导致其出力的随机性,通过概率潮流计算出电力系统中各节点电压和各支路潮流的概率统计特性[7-9]。相比传统的确定性潮流计算,更加准确地计算出实际结果。
求解概率潮流的方法主要包括模拟法、解析法和近似法。模拟法主要是指随机采样蒙特卡罗模拟法[10-11],它的思想是将系统中的随机因素进行模拟,然后进行大规模反复的抽样。其最大问题是需要进行大量的反复抽样过程,计算周期非常长。解析法是将随机变量输入和输出的关系近似线性化数学假设,然后进行卷积运算,其关键步骤是有效地对系统方程卷积计算与化简。卷积法利用输入变量的概率分布函数得到输出变量的概率密度函数。除卷积法外,解析法计算速度快,但含有较大的误差。解析法概率潮流主要有半不变量法。近似法主要是通过随机变量的概率分布或概率密度,近似求取目标函数的概率统计特征(原点矩、中心矩),这其中主要以点估计[12-13]和一次二阶矩法[14]为代表。在这3种方法中,蒙特卡罗方法可直接仿真待求随机变量的概率分布,而解析法和近似法需计算出矩或半不变量之后,通过级数展开求得概率分布,但其在近似表达非正态概率分布时,存在一定的误差。
本文将结合解析法与近似法提出基于2n+1点估计法与半不变量、Gram-Charlier级数的概率潮流算法,求取在分布式电源随机功率注入条件下的节点电压幅值的数字特征,最后得到节点电压的概率密度函数,对含分布式电源的配电系统电压质量进行概率评估。以接入风电场和光伏电源的IEEE-30节点系统为算例进行随机潮流计算,得到各节点电压和各支路潮流的概率分布,并且分析了分布式电源接入前后对系统节点电压的影响,通过计算和比较得出该方法的有效性及实用性。
1 分布式电源的出力以及负荷水平概率分布模型
1.1风电机组出力的概率分布模型
1.1.1风电机组有功功率输出模型
风电场风力发电机组有功出力值与风电场风速之间满足以下数学表达式为:

式中:vci、vr、vco分别为风电机组的切入风速、额定风速以及切出风速;Pwind为风力发电机组的随机功率;Pr为风力发电机组的额定出力;a=Prvci/(vci-vr),b=Pr/(vr-vci),a,b为常数。
1.1.2风力风速的概率分布模型
风速具有很强的随机性,从而使风机的出力也具有很强的随机性。大量相关实际数据验证显示,较多地区的平均风速服从双参数Weibull分布函数[6],其PDF表达式为:

式中:v为风速;K为形状参数,K=(σ/μ)1.086,σ为标准差;c为尺度参数,C=μ/[Γ(1+1/K)],其中μ为平均风速,Γ为Gamma函数。
将风电机组有功功率输出模型与风力风速的的概率分布模型相结合,得到风力发电机组随机出力分布模型,其PDF表达式为:

风力发电机作为分布式电源,其控制方式为恒功率因数控制,看作PQ节点,则风力发电机组随机无功出力的分布模型为:
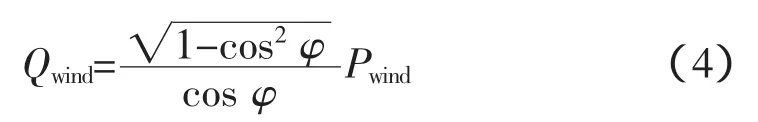
1.2光伏发电出力的概率分布模型
1.2.1光伏发电的出力模型
太阳能作为自然界的一种可再生能源,具有随机性、间歇性、不确定性等特点,光照辐射强度、光伏阵列面积及光电转换效率共同决定了光伏发电的出力,则光伏发电总出力表达式为:

式中:r为光照辐射强度;A为光伏阵列总面积;η为总体转换效率。
1.2.2光照强度的概率分布模型
太阳能光伏电池的出力受光照强度影响而变化。对大量相关实际统计数据检验的结果表明,光伏电池的光照强度满足Beta分布,其PDF可描述为:
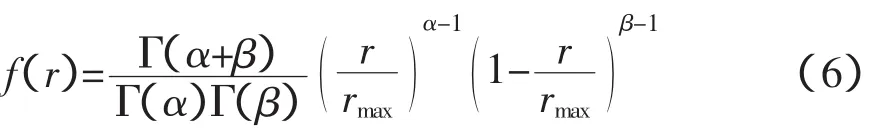
式中:rmax为最大辐射强度;Γ为Gamma函数;α、β分别为Beta分布参数,取值分别为,其中μ为光照强度的均值,σ为标准差。
由光伏阵列的功率输出表达式(5)和光照辐射强度的概率分布模型(6)可以得到光伏发电出力的PDF:
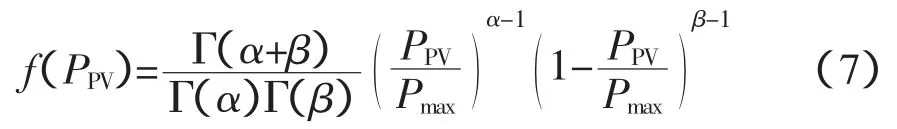
式中:Pmax=rmaxAη为在光伏阵列面积时的输出功率。
在太阳能光伏发电出力模型中,光伏发电被看作PQ节点。可以考虑只向系统网络输入有功功率,然而不计及无功功率。
1.3负荷随机模型
负荷具有不确定性的特点,根据长时期大量相关实际数据的统计表明,系统负荷的随机分布大体服从正态分布,μP是负荷有功均值,μP是负荷无功均值,σP2是负荷有功方差,σQ2是负荷无功的方差,则其有功功率和无功功率的PDF为:

2 2n+1点估计法
2.1点估计法的原理
点估计法,其基本原理是在随机输入变量的基础上选择具有离散性的估计点,根据输入随机变量的概率密度函数估计求取输出随机变量的数字特征,如期望、方差和各阶矩等[15]。设X为一个已知连续的随机输入变量,其PDF为fX(x),设Y=h(x)是基于x的非线性函数。而点估计法的基本思想是通过函数h(x)的前几阶矩等概率统计量,用m个概率集合来代替h(x)。若随机输入变量X的维数是n维时,此时点估计法的联合概率密度就可以用m×n个概率集合来代替,从而可以计算出采用了m×n个估计点。
2.22n+1点估计法
对于点估计法而言,其关键和核心是估计点的提取个数m,一般来讲,估计值Y的精度随着m取值个数的增加而增大。然而在工程实际应用中,每一个估计点对应的计算量是n次,使得计算负担增大。并且,m值每增长1个,Xi的计算过程中就要求解更高一阶中心矩。然而4阶及以上求解出的中心矩λi,j值并没有什么实际意义,另外还导致了求解出的位置度量系数ξi,k和权重wi,k是非实数解。综上分析,Xi的中心矩阶数不大于3时,换言之,采用2n个点进行估计[16]。
当m=3,则在输入随机变量Xi取3个点作为估计点,从中选取一个估计点使其取均值μi,对应的位置度量系数ξi,3=0。尽管构造了3n个估计点,但其中有n个点对应同一估计点向量(μ1,μ2,…,μi,…,μn),而只需计算一次Y值,因此3n点估计转变为2n+1点估计。2n+1点估计比2n点估计精度要高,由于它考虑了输入随机变量的λi,3和λi,4,但计算量仅增加1次函数值的计算。
设多元函数Y=f(x)有n维随机变量(x1,x2,…,xn)在各个变量中取m个估计点上对Y作m×n次估计。2n+1点估计法就是在每一个输入随机变量的期望值以及它的两侧同时取值。随机变量之间是相互独立的,随机输入变量xi的均值和标准差分别用μi和σi表示,ξi,k为位置度量系数。k为取点个数。每个随机变量的均值及其两侧取值方法为:

设λi,j为xi第j中心距Mj(xj)和标准差σi的j次方之比,即:
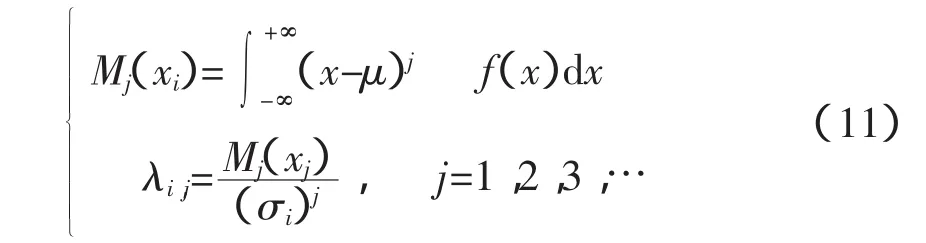
当k=3时,ξi,3=0,表示在均值取点,即xi,3=μxk;r= 1,2时,
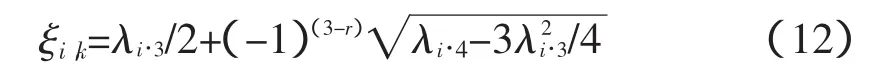
xi,1和xi,2在均值右邻域和左邻域取点,λi,3与λi,4分别称为随机变量Xi的偏度与峰度系数:

式中:E[(Xk-μxk)3]和E[(Xk-μxk)4]分别为随机变量集合Xk的三阶中心距与四阶中心距。
节点注入功率随机变量的个数为z个,用式(10)确定的3个估计点来分别代替随机变量xi,然后其他节点注入功率取均值,进行3次确定性潮流计算,可以得到待求解某变量Yi的3个估计值Y(i,1)、Y(i,2)、Y(i,3)。在z个随机输入变量中,每个随机输入变量的权重为1/Z,针对某一随机变量集合Xi,所取估计点xi,k的权重为wi,k,
wi,k可由式(14)计算:
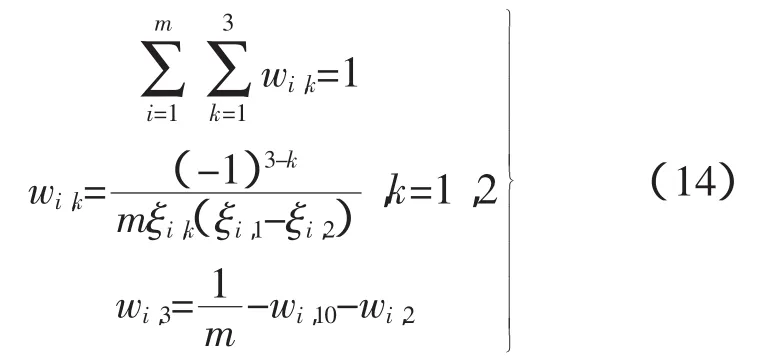
联立求解,得到每个估计点权重wi,k后可计算Yi的j阶原点矩值:

当j=1时,E(Y)是Y的均值,当j=2时,则有Y的标准差:

3 半不变量及Gram-Charlier级数
3.1半不变量
在随机变量的矩以及半不变量已知的条件下,可以计算出随机变量的均值、方差、偏度系数以及峰度系数。该随机变量的概率分布函数可以采用级数展开法求解。如果χl为变量X的l阶半不变量,那么χl与变量X的l阶原点矩E(Xl)满足以下关系:
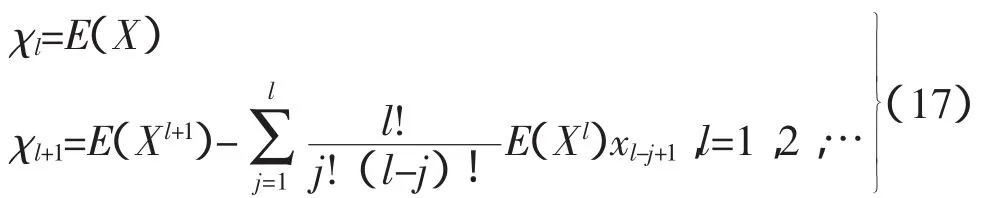
3.2Gram-Charlier级数展开
Gram-Charlier级数展开法可以利用随机输入变量的各阶矩或者各阶半不变量,将随机变量的概率密度函数和概率分布函数表达为由正态随机变量各阶导数组成的级数。经过标准化之后的随机变量X的PDF和CDF,其表达式分别如下:
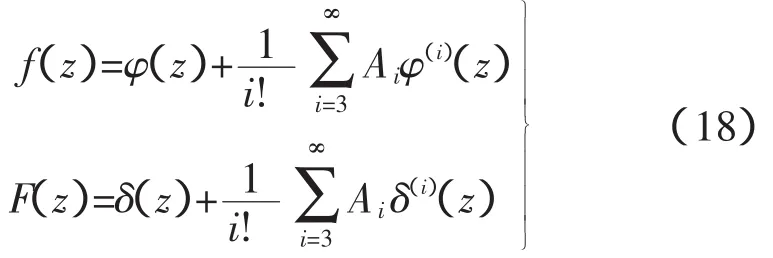
式中:φ(z)和δ(z)分别是标准正态分布的密度函数和分布函数;φ(i)(z)和δ(i)(z)分别是其i阶导数,系数Ai和Z的t阶半不变量的关系如下:

4 配电网电压质量概率评估计算过程
根据第1节建立的分布式电源出力的概率模型,应用基于2n+1点估计法的概率潮流算法,结合半不变量及Gram-Charlier级数展开,对分布式电源接入的配电系统电压质量进行概率评估,具体步骤如下:
1)输入系统初始数据,包括常规发电机参数,系统支路参数。
2)计算风速服从Weibull分布,光照强度服从Beta分布的参数,根据式(3)、式(7)、式(8)分别得到风力发电、光伏发电功率输出的概率密度函数,同时根据式(9)得到负荷功率输出的概率密度函数。由式(11)计算其随机变量的中心距λi,j、偏度系数与峰度系数。
3)根据本文中提出的2n+1点估计法选取估计点,利用式(12)得到每个选取的估计点所对应的位置系数。再由式(10)计算出每个随机变量的均值及其两侧取值,并计算平均功率下的估计点的功率输出。
4)对分布式电源接入的配电系统进行潮流计算,计算节点在随机功率注入情况下的节点的电压幅值。
5)根据式(14)分别计算选取的估计点所对应的权重系数wi,k,利用式(15)得到节点电压的各阶原点矩。
6)根据式(17)利用节点电压各阶原点矩,计算节点电压的各阶半不变量,结合Gram-Charlier级数,通过级数展开式求解出节点电压的概率密度函数。
2n+1点估计法随机潮流计算流程图如图1所示。
5 算例分析
本文以含有分布式电源的IEEE-30节点配电系统作为算例,在末端节点处分别接入分布式电源,计算分布式电源接入配电系统时的概率潮流分布。采用的方案则是在节点3处接入一台风力发电机,在节点14处接入一组太阳能光伏电池阵列,此外在节点26处同时接入由一台风力发电机和一组太阳能光伏电池阵列组成的风-光互补电场,具体的系统接线图如图2所示。

图1 点估计法随机潮流计算流程图Fig.1 Flow chat of 2n+1 point estimate method
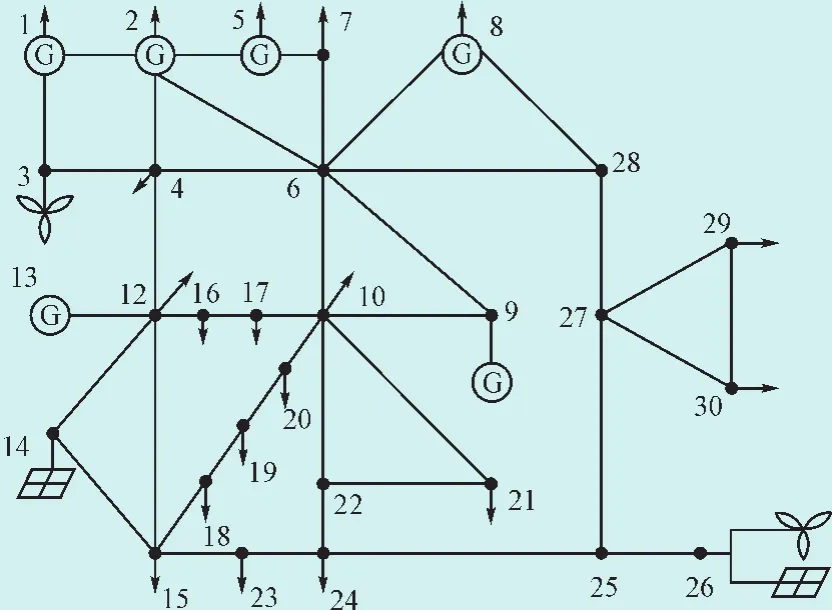
图2 IEEE 30节点系统图Fig.2 IEEE 30 node test system
IEEE-30节点系统相对复杂,接入节点系统共发电机6台,有20个负荷,在仿真过程中6台发电机的参数都服从二项分布,系统节点参数服从正态分布,以标准负荷值作为负荷期望值,方差为其10%,设节点负荷的注入量相互独立。有关分布式电源的数据如表1、表2所示。
仿真系统中设节点1为平衡节点,PV节点有5个,分别是节点2,5,8,9,13,剩余节点可当做PQ节点,分布式电源的功率输出为负。输入系统初始数据,包括常规发电机参数、系统支路参数、风机光伏参数等数据,根据基于2n+1点估计法的概率潮流求解的计算流程求出在随机功率注入情况下各个节点以及接入分布式电源节点的电压幅值和标准差,分别计算选取的估计点所对应的权重系数,再进而得到节点电压的各阶原点矩然后计算节点电压的各阶半不变量。表3是计算得出的部分节点的均值和标准差。

表1 风电机参数Tab.1 Parameters of wind turbine generators

表2 光伏电池组的相关参数Tab.2 Parameters of PV arrays

表3 部分节点电压均值和标准差Tab.3 Mean value and standard deviation of voltage magnitude for parts of buses
得到节点电压的概率统计特征、均值、方差和各阶原点矩的数值后,应用半不变量及Gram-Charlier级数展开可以求解得出节点电压概率密度曲线。节点3、14、26并入分布式电源前后节点的概率密度曲线分别如图3—图5所示。
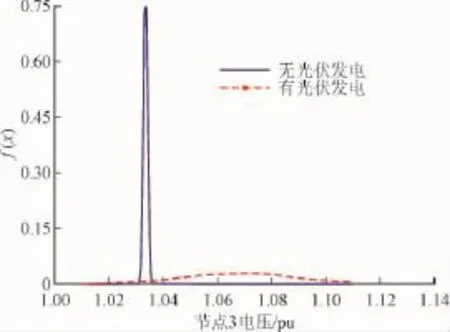
图3 节点3电压幅值概率密度曲线Fig.3 PDF curve of voltage magnitude for Bus 3

图4 节点14电压幅值概率密度曲线Fig.4 PDF curve of voltage magnitude for Bus 14

图5 节点26电压幅值概率密度曲线Fig.5 PDF curve of voltage magnitude for Bus 26
从仿真图像上可以看出:分布式电源的接入对系统电压质量造成严重影响。图中的横坐标为节点电压的标幺值,电压幅值的越限概率合格范围为0.95~1.05,图中尖锐的曲线代表无分布式电源接入的情况,电压幅值在合格范围内,没有产生电压越限。当接入风电场或光伏电场单独并入系统节点3,节点14处时,电压幅值变化从到1.01~1.11,超出了电压幅值合格范围,电压越限概率明显增加。由于节点26具有“风光互补”的优势,因此该节点的电压越限概率较小,对电能质量的影响也相对的减少。
6 结语
本文提出了基于2n+1点估计法与半不变量,Gram-Charlier级数的概率潮流算法,建立了接入配电网的分布式电源的出力概率模型和负荷水平的概率模型,求取在随机功率注入条件下的节点电压幅值的数字特征,最后得到节点电压的概率密度函数,对含分布式电源的配电网电压质量进行概率评估。以含有分布式电源的IEEE-30节点系统作为算例,用2n+1点估计法进行概率潮流计算,分析了分布式电源接入前后对系统节点电压的影响。
[1]谷永刚,王琨,张波.分布式发电技术及其应用现状[J].电网与清洁能源,2010,26(6):38-43.GU Yonggang,WANG Kui,ZHANG Bo.Distributed generation technologies and their current applications[J].Power System and Clean Energy,2010,26(6):38-43(in Chinese).
[2]戎晓雪,别朝红,石文辉,等.考虑风电场相关性的含风电电力系统随机潮流分析[J].电网技术,2014,38(8):2161-2167.RONG Xiaoxue,BIE Zhaohong,SHI Wenhui,et al.Analysis on probabilistic load flow in power gird integrated with wind farms considering correlativity among different wind farms[J].Power System Technology,2014,38(8):2161-2167(in Chinese).
[3]AHMED M H,BHATTACHARYA K,SALAMA M M A.Probabilisti-c distribution load flow with different wind turbine models[J].IEEE Transactions on Power Systems,2013,28(2):1540-1549.
[4]张硕,李庚银,周明.含风电场的发输电系统可靠性评估[J].中国电机工程学报,2010,30(7):8-14.ZHANG Shuo,LI Gengyin,ZHOU Ming.Reliability assessment of generation and transmission systems integrated with wind farms[J].Proceedings of the CSEE,2010,30(7):8-14(in Chinese).
[5]朱益华,罗毅.基于输电线路实时评估模型的电力系统静态安全在线风险评估[J].电力自动化设备,2014,34(7):150-157.ZHU Yihua,LUO Yi.Integrative evaluation model of node vulnerability considering network transmission ability and anti-interferenceability[J].ElectricPowerAutomation Equipment,2014,34(7):150-157(in Chinese).
[6]SU C L.Stochastic evaluation of voltages in distribution net-works with distributed generation using detailed distribution operation models[J].IEEE Trans on Power Systems,2010,25(2):786-795.
[7]朱星阳,刘文霞,张建华.考虑大规模风电并网的电力统随机潮流[J].中国电机工程学报,2013,33(7):77-85.ZHU Xingyang,LIU Wenxia,ZHANG Jianhua.Probabilistic load flow method considering large-scale wind power integration[J].Proceedings of the CSEE,2013,33(7):77-85(in Chinese).
[8]高元海,王淳.基于全概率公式的含风电配电系统概率潮流计算[J].中国电机工程学报,2015,35(2):327-334.GAO Yuanhai,WANG Chun.Probabilistic load flow calculation of distribution system including wind farms based on total probability formula[J].Proceedings of the CSEE,2015,35(2):327-334(in Chinese).
[9]张楷旋,陈建英.考虑天气因素的含风电场电力系统的概率潮流分析[J].电网技术,2014,38(12):3418-3423.ZHANG Kaixuan,CHEN Jianying.Weather factor based analysis on probabilistic load flow of power grid containing wind farms[J].Power System Technology,2014,38(12):3418-3423(in Chinese).
[10]JORGENSEN P,CHRISTENSEN J S,TANDE J O.Probabilistic load flow calculation using monte carlo techniques for distribution network with wind turbines[C].Proceedings of IEEE Conference on Harmonics and Quality of Power.Athens,Greece,1998:1146-1151.
[11]丁明,李生虎,黄凯.基于蒙特卡罗模拟的概率潮流计算[J].电网技术,2001,25(11):10-14.DING Ming,LI Shenghu,HUANG Kai.Probabilistic load flow analysis based on Monte-Carlo simulation[J].Power System Technology,2001,25(11):10-14(in Chinese).
[12]VERBIC G,CANIZARES C.Probabilistic optimal power flow in electricity markets based on a two-point estimatemethod[J].IEEE Trans on Power Systems,2006,21(4):1883-1893.
[13]MORALES J M,PEREZ-RUIZ J.Point estimate schemes tosolve the probabilistic power flow[J].IEEE Trans on Power Systems,2007,22(4):1594-1601.
[14]LI Xue,LI Yuzeng,ZHANG Shaohua.Analysis of probabilistic optimal power flow taking account of the variation of load power[J].IEEE Trans on Power Systems,2008,23(3):992-999.
[15]张鑫.含分布式电源的配电系统概率可靠性评估[D].天津:天津大学,2013.
[16]HONG H P.An efficient point estimate method for probabilistic analysis[J].Reliability Engineering and System Safety,1998,59(3):261-267.
[17]王敏,丁明.考虑分布式电源的静态电压稳定概率评估[J].中国电机工程学报,2010,30(25):17-22.WANG Min,DING Ming.Probabilistic evaluation of static voltage stability taking account of distributed generation[J].Proceedings of the CSEE,2010,30(25):17-22(in Chinese).
[18]张喆,李庚银,魏军强.考虑分布式电源随机特性的配电网电压质量概率评估[J].中国电机工程学报,2013,33(13):4.ZHANG Zhe,LI Gengyin,WEI Junqiang.Probabilistic evaluation of voltage quality in distribution networks considering the stochastic characteristic of distributed generators[J].Proceedings of the CSEE,2013,33(13):4(in Chinese).
[19]寇凤海.分布式光伏电源对配电网网损的影响[J].电网与清洁能源,2011,27(11):62-68.KOU Fenghai.Impacts of distributed photovoltaic power sources on distribution network loss[J].Power System& Clean Energy,2011(in Chinese).
[20]张雪莉,刘其辉,马会萌,等.光伏电站输出功率影响因素分析[J].电网与清洁能源,2012,28(5):75-81.ZHANG Xueli,LIU Qihui,MA Huimeng,et al.Analysis of influencing factors of output power of photovoltaic power plant[J].Power System&Clean Energy,2012,28(5):75-81(in Chinese).
[21]孙红霞,赵彩宏.光伏/风电并网测试装置的设计和开发[J].高压电器,2014(5):103-109.SUN Hongxia,ZHAO Caihong.Design and development of testing devices for photovoltaic/wind power grid connection[J].High Voltage Apparatus,2014,50(5):103-109(in Chinese).
(编辑冯露)
Probabilistic Evaluation of Voltage Quality on 2n+1 Point Estimate Method for the Distribution System Containing Distributed Generation
CHEN Wei,GUO Qiuchi,PEI Xiping
(College of Electrical Engineering and Information Engineering,Lanzhou University of Technology,Lanzhou 730050,Gansu,China)
To evaluate the impact on the power quality of distribution system by the stochastic power output of distributed generators and loads,this paper proposes a 2n+1 point estimate method based on the present point estimate method.This method takes into account the wind speed and illumination intensity and the influence of load stochastic characteristic of distribution network.The probabilistic statistic values of voltages would be derived via the solution of probabilistic load flow.Combined with theory of semi-invariant and Gram-Charlier series expansion,the probabilistic evaluation for voltage quality of the distribution network with distributed generators is obtained with the relative probability distribution function curves and the probability of voltage out of limit.Taking the IEEE 30-bus system containing distributed generation as the case,the influence on the node voltages of system before and after the distributed generation are analyzed.
distributed generators;voltage quality;probabilistic load flow;2n+1 point estimate;probability density function
1674-3814(2016)07-0023-07
TM76
A
国家自然科学基金项目(51267012);甘肃省科技支撑工业计划项目(1504GKCA033);甘肃省自然科学基金项目(1308RJZA245,1310RJYA079)。
Project Supported by National Natural Science Foundation of China(51267012);Science and Technology Infrastructure Program of Gansu province(1504GKCA033);Natural Science Foundation of Gansu province.(1308RJZA245,1310RJYA079).
2016-03-05。
陈伟(1976—),男,博士,教授,博士生导师,研究方向为电能质量分析与控制;
郭秋池(1990—),男,硕士,研究方向为电能质量分析与控制。
