基于隐马尔可夫模型的信息系统风险评估方法
2016-11-10盛剑会郑秋生
潘 恒, 盛剑会, 郑秋生
(中原工学院, 郑州 450007)
基于隐马尔可夫模型的信息系统风险评估方法
潘恒, 盛剑会, 郑秋生
(中原工学院, 郑州 450007)
为保障信息系统安全,必须定期进行风险评估,但通常是对照测评标准逐项测评后给出测评结论,因缺乏精确的数学模型指导而受主观因素影响较大。为此,对信息系统风险评估过程建立了隐马尔可夫模型。在建模过程中,对输出值矩阵进行简化处理,并以随机产生的观察值序列作为隐马尔可夫模型训练数据。学习训练后的模型可利用前向算法自动评估系统当前的安全状态。应用实例说明:该方法贴近实际测评工作流程,是一种有效的风险评估方法,可在一定程度上提高评估的科学性,降低测评人员工作量,同时适用于信息系统安全风险自评估。
信息系统; 安全风险评估; 隐马尔可夫模型; 安全测评标准; 前向算法
信息系统风险评估是通过检查信息系统资产脆弱性及可能存在的威胁,对其总体风险做出正确的估计[1]。信息系统风险评估是保障系统安全的重要环节,但目前理论研究与实际评估存在脱节。实际的风险评估工作主要是依据国家相关测评标准,采用问卷调查、工具扫描、专家评估等方式对信息系统进行逐项检查[2]。然而,目前理论研究主要侧重于采集入侵检测、病毒检测、日志信息等工具的报警信息,利用模糊层次分析法、贝叶斯网络、信息熵、D-S证据理论、隐马尔科夫模型等方法建立风险评估或安全态势评估模型,特别关注评估模型的框架、评估策略以及评估推理等问题。现有文献特别缺少基于国家标准又与实际风险评估工作方式贴近的精确数学模型。
基于标准的风险评估,需要依据安全测评标准对信息系统进行逐项检测、打分,各项分值主观性较强。此外,主要采用定性分析或简单加权的方法汇总各测评项分值,统计结果存在很大的不确定性。为了利用数学方法和模型来处理上述问题,本文引入隐马尔可夫模型(Hidden Markov Model,HMM)对基于标准的信息系统安全风险评估过程进行建模。
Arnes A等人提出了基于HMM的网络风险评估方法,将网络风险视为主机风险之和,将主机状态描述为安全、被探测、被攻击、攻破4种,并建立相应的状态转移矩阵;将主机遭受到的攻击作为观察序列,并建立观察矩阵[3]。上述思想衍生出很多网络风险评估方法[4]。但是,这些方法在评价网络风险大小时,均引入了主机处于某个状态的风险度(cost value)。实际上,该值的获取存在困难,使得这些方法很难应用于实际检测过程。Krugel C等人提出了将HMM应用于网络攻击的检测方法,将基于HTTP协议的网络应用层请求划分为不同的属性类别,根据非法攻击一般含有非法字符串请求这一特点,建立起正常服务请求的学习和训练模型,来检测对网络应用服务的攻击行为[5]。杨晓峰等人对以上学习模型进行了改进和优化,提高了算法的检测性能,但是仍仅用于网络应用程序的安全检测,无法对信息系统安全进行全面检测[6]。此外,利用HMM进行主机安全威胁检测方面的研究成果也较多,通过建立程序正常行为的HMM学习及训练模型,来检测异常程序,并由此判断主机的安全状况[7-8]。这些研究仅考虑主机安全而未能考虑网络及整个信息系统的风险评估。
本文参考上述文献建立HMM双重随机过程的思路,拟用HMM模型对目标信息系统进行安全风险评估,定量获取信息系统的当前安全状态,从一定程度上提高评估过程的自动性和科学性。
1 基于安全测评标准的HMM模型定义
隐马尔科夫模型是一个双重随机过程[9]。其中一个是显式随机过程,可以通过输出序列直接观察,符合模型中输出概率分布矩阵;另一个是隐式随机过程,它是一个一阶马尔科夫链,符合模型中的状态转移矩阵。两重随机过程的关系是:虽然隐式的马尔科夫过程无法直接观察,但可以利用显式输出序列,通过HMM模型中的输出概率分布和状态转移矩阵来推测。
根据实际测评经验,目标信息系统安全风险评估的最终结果通常可分为3种:安全、基本安全和不安全。本文将这3种风险评估结果看作信息系统的3种安全状态。安全风险评估是定期实施的,根据国家有关测评标准对系统资产、威胁以及脆弱点等进行逐项检查,而信息系统每次评估的最终结果不是一成不变的,存在一定的转移关系。因此,信息系统的安全状态就构成了HMM模型的一重隐含随机过程;且测评标准中各测评项的测评被看作另一重可以被观察到的显式随机过程。由于信息系统安全状态的评估结论是由众多测评值综合得到的,即可以从测评项的测评分值推测出隐含着的系统安全状态,因此,可以建立一套信息系统安全风险评估的隐马尔可夫模型,以自动评估信息系统的安全状态。
定义1目标信息系统安全状态集合为S={G,B,C},其中:G代表安全状态;B代表基本安全状态;C代表不安全状态。
定义2目标信息系统安全测评项的某个可能测评结果为vi,测评结果集合为V={vi},i=1,2,…,m。
定义3目标信息系统的安全测评隐马尔科夫模型λ=(S,V,A,B,π),其中:
(1)V是定义2给出的各测评项的测评结果集合;
(2)A是目标信息系统状态转移矩阵:
A=[aij]
aij=P(qt+1=j|qt=i),i,j∈S
(3)B是各测评项的测评输出结果的概率分布:
B={bj(k)}
bj(k)=P(vk|j),1≤k≤m,j∈S
bj(k)表示在状态j时输出某测评项的测评结果为vk的概率;
(4)π是目标信息系统安全初始状态的概率分布:
π={πi},i∈S
πi=P(q1=i)表示初始时刻处于某一状态的概率。
定义4目标信息系统的测评项观察序列(即输出测评值序列)为O,O=(o1,o2,…,ot,…,oT),其中ot∈V,t∈[1,T]。
设测评标准共有n个测评项,若根据标准对测评项逐一检查,则T=n;若仅对标准中的重点测评项进行有选择的检查,则T 按照上述定义建立信息系统安全风险评估的HMM模型。模型的建立过程分为学习和检测两部分。在学习部分,首先根据测评经验随机生成符合三种状态的训练数据,然后采用Baum-Welch算法对模型参数进行学习训练。在检测部分,对目标系统实际测评分值进行分类规范化处理后,依次输入系统状态安全、系统状态基本安全和系统状态不安全3个HMM模型,利用前向算法分别计算出3个模型的值。值最大的模型所对应的安全状态就是目标信息系统当前的安全状态。 2.1观察值序列的生成 信息系统安全风险评估一般是参照有关安全测评标准,逐一对各测评项进行检测、打分,每个测评项的分值要精确到小数点后几位,最后汇总所有测评项分值才能得到整个系统的安全状况。而汇总方法主要采用简单加权法,系统满分为100分。总分80分以上的系统为安全系统;60~80分的系统为基本安全系统;小于60分的是不安全系统。这样的测评过程过于复杂,工作量及主观性较大。 根据每个测评项分值高低,将各测评项的值规范化为“好”“中”“差”三级来代替精确到小数点后几位。为了方便讨论,本文假设各测评项的满分分值均为1,将测评项的分值大于0.8的视为“好”,在0.6和0.8之间的视为“中”,小于0.6的视为“差”。规范化后,不仅测评过程更加简单,而且测评的主观性在一定程度上降低,同时输出值矩阵降为3行3列,大大降低了HMM模型观察值矩阵的维数。 本文在构建HMM学习训练模型时,未采用大量实际测评数据,而是根据测评规律随机生成观察值序列。这样取得的测评数据量大且随机性好。在训练数据时,分别用1、0、-1代表某一测评项的测评结果的“好”“中”“差”。根据前期对测评人员的访谈,在对各测评项进行测评时,若某测评项合格,则分值为1;若某测评项基本合格,则分值一般会在0.6~0.8之间;若某测评项不合格,则最差的分值为0,其余的一般在0.3~0.6之间。根据上述经验,假设目标系统中测评项测评结果为“好”的项数为x,为“中”的项数为y,为“差”的项数为z。测评项测评结果为“好”,其分值为1;测评项测评结果为“中”,其分值取平均值0.7;测评项测评结果为“差”,其分值取平均值0.45,考虑到有少量特别差的测评项分值为0,因此修正其平均值为0.4。 这样,若目标信息系统的状态为安全,各测评项的分值之和应大于80分,则应满足: x+0.7y+0.4z≥80 (1) 若目标信息系统的状态为基本安全,各测评项的分值之和应满足: 60≤x+0.7y+0.4z<80 (2) 若目标信息系统的状态为不安全,各测评项的分值之和应满足: x+0.7y+0.4z<60 (3) 利用上述公式,可生成大量随机特性良好的训练数据。 根据上述分析,测评项分值规范化为“好”“中”“差”后,给出安全自评估HMM模型的定义。 定义5目标信息系统的安全自评估隐马尔科夫模型λ=(S,V,A,B,π),其中: (1)V是定义2给出的各测评项的测评结果集合,测评项分值规范化为“好”“中”“差”后,V={vi},i=1,2,3; (2)A是目标信息系统状态转移矩阵: A=[aij] aij=P(qt+1=j|qt=i),i,j∈S (3)B是各测评项的测评结果输出的概率分布: B={bj(k)} bj(k)=P(vk|j),1≤k≤3,j∈S bj(k)表示在状态j时输出某测评项的测评结果为vk的概率; (4)π是目标信息系统安全初始状态的概率分布: π={πi},i∈S πi=P(q1=i)表示初始时刻处于某一状态的概率。 2.2HMM模型参数的学习训练 分别设定3个HMM模型的A、B、π,将生成的观察值序列代入Baum-Welch算法,对HMM模型参数进行学习训练。这里以其中一个HMM模型为例介绍该算法。 第一步,设置模型参数值A、B、π,使其满足下列式子: (4) (5) (6) 第二步,输入大量随机生成的观察值序列,计算ξt(i,j)和γt(i),以备重新修正。 ①计算变量1: ξt(i,j)=P(qt=i,qt+1=j|O,λ) (7) 其中: at(i)=πibi(ot) βT(i)=1 1≤i,j≤3,1≤t≤T-1 ②计算变量2: (8) (9) (10) 其中:当ot=vk时,δ(ot,vk)=1;当ot≠vk时,δ(ot,vk)=0。即当观察序列的值与输出值vk相同时,δ(ot,vk)=1;否则δ(ot,vk)=0。 2.3自动检测方法 利用修正好的3个HMM模型来检测某一信息系统的安全状况。 该算法伪代码为: Fori=1 to HMM-num //其中HMM-num为隐马尔科夫模型数量,这里HMM-num=3 { Pro=P(O′|λi)//利用前向算法计算3个在HMM模型中产生的上述测评项序列的概率 } Output=Max(Pro) //概率最大的HMM模型代表该信息系统的安全状态 这里以某高校安全评估实验室的信息系统为例,以Matlab6.5模拟方法实现BW算法和前向算法,介绍利用HMM模型进行信息系统安全自评估的方法和流程。 第一步,给出HMM模型的初始参数λ0。 状态转移矩阵A如表1所示。 表1 初始状态转移矩阵A 测评输出结果的概率B如表2所示。 表2 测评输出结果的概率B 第二步,通过学习训练,建立“安全”“基本安全”“不安全”3个HMM模型。 为简化描述,这里仅给出“安全”状态的信息系统自评估HMM模型的建立过程。 生成满足式(1)的由-1、0、1组成的序列,序列长度为10 000条。取信息系统自评估测评项数为200(即每组观察序列长度为200条),则这10 000条数据相当于模拟了50个信息系统的实际测评分值,即50组训练数据。 表3 修正后的状态转移矩阵 表4 修正后的输出结果的概率 按上述过程可分别建立“基本安全”和“不安全”两个HMM模型。3个模型被建立后即可进行系统自评估检测。 第三步,某高校安全实验室的80条测评项分值按照每项≥0.8分为“好”,0.6~0.8分为“中”,0.6分及以下为“差”,进行规范化。规范化后的结果如表5所示。将表5数据代入训练后的3个HMM模型,并利用Matlab模拟HMM前向算法,计算出3个HMM模型的概率(见表6)。 表5 测评项分值规范化后结果 表6 3个HMM模型观察值概率P(O|λ)值 从表6可以看出,某高校安全实验室的测评结论应为基本安全。 从应用实例可以看出,该方法与基于信息系统安全测评标准的安全风险评估的实际测评过程吻合度高。由于随机生成的训练数据较为均匀,HMM模型的训练过程较为简单,可在一定程度上提高信息系统安全风险评估的客观性。该方法无需对所有测评项进行评估,就可自动地评估信息系统的安全状况,因此也适用于信息系统安全风险的自评估。 信息系统安全风险评估存在理论与实际工作的偏差,特别是缺少基于国家测评标准的精确评估模型。针对这一问题,本文将HMM模型应用于标准的实际信息系统安全风险评估过程。在实际建模过程中提出具体简化测评项打分和HMM学习训练的方法,可方便获得系统是否安全的结论。该方法根据测评经验和标准要求对重点测评项进行检测,用于信息系统安全风险自评估,克服了以往信息系统自评估必须对所有测评项进行检测汇总后才能获得系统安全状况的问题,在一定程度上减轻了安全风险评估的工作量。 [1]Yang J, Liang L, Yang Y. A Hierarchical Network Security Risk Assessment Method based on Vulnerability Attack Link Generated[C]//Fourth International Symposium on Information Science and Engineering IEEE Computer Society. Washington: IEEE,2012:113-118. [2]王祯学,周安民,方勇,等. 信息系统安全风险评估与控制理论[M]. 北京:科学出版社,2011:13-17. [3]Arnes A, Valeur F, Vigna G, et al. Using Hidden Markov Models to Evaluate the Risks of Intrusions[M]. Berlin: Recent Advances in Intrusion Detection, 2006:145-164. [4]陈天平,许世军,张串绒,等.基于攻击检测的网络安全风险评估方法[J].计算机科学,2011,37(9):94-96. [5]Kruegl C, Vigna G. Anomaly Detection of Web-based Attacks[C]//Proc. of the 10th ACM Conference on Computer and Communications Security. Washington: ACM, 2010:251-261. [6]杨晓峰,孙明明,胡雪蕾,等. 基于改进隐马尔科夫模型的网络攻击检测方法[J].通信学报,2010,31(3): 95-100. [7]邬书跃,田新广.基于隐马尔可夫模型的用户行为异常检测新方法[J].通信学报,2007,28(4):38-43. [8]Wang W, Guang X, Zhang X. A Novel Intrusion Detection Method Based on Principe Component Analysis in Computer Security[C]//Proc. of Advances in Neural Networks, International IEEE Symposium on Neural Networks. Washington: IEEE, 2004:657-662. [9]Yariv E, Neri M. Hidden Markov Process [J]. IEEE Transactions on Information Theory, 2002,48(6): 1518-1566. (责任编辑:王长通) Risk Assessment Approach for Information System Security Based on HMM PAN Heng, SHENG Jian-hui, ZHENG Qiu-sheng ( Zhongyuan Universtiy of Technology, Zhengzhou 450007, China) In order to guarantee security, the risk of information system is needed to be regularly estimated. However, the real estimation method is usually to evaluate the system term by term under the secure assessment standard. Bacause of lack of precise mathematical model, such process is limited both estimation procedure and result subjective to some extent. Focusing on these problems,this paper takes use of Hidden Markov Model (HMM) to build a mathematical model on procedure of information system risk assessment, which could automatically estimate the security state of the information system based on secure assessment standard. First, the HMM output value matrix is simplified. An observation value generating algorithm is proposed, which could be regarded as HMM model training data. After training, HMM model can be used to evaluate secure state of the target information system. The application project shows that this method can work effectively and is close to the real secure assessment procedure, which can reduce the workload and improve the assessment scientific extent that can be used in risk self-assessment. information system; risk assessment; Hidden Markov Model; secure evaluation standard; forward algorithm 2016-06-27 河南省科技攻关项目(132102310284);郑州市科技创新团队项目(131PCXTD600);郑州市普通科技攻关项目(132102210186) 潘恒(1977-),女,河南新乡人,副教授,博士,主要研究方向为信息系统安全评估。 1671-6906(2016)04-0085-06 TP309 A 10.3969/j.issn.1671-6906.2016.04.0182 基于安全测评标准的HMM风险评估模型

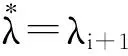
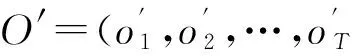
3 应用实例







4 结 语
