压缩感知中图像重构的模型综述
2016-11-10宋长明惠庆磊
宋长明, 惠庆磊
(中原工学院, 郑州 450007)
压缩感知中图像重构的模型综述
宋长明, 惠庆磊
(中原工学院, 郑州 450007)
分别从稀疏表示、编码测量以及重构算法等方面阐述了压缩感知的基本原理。基于概率、凸优化等详细介绍了图像重构模型的理论框架和发展状况,并从字典学习和低秩表示的角度展望了图像重构模型进一步研究的方向。
压缩感知;图像重构;凸优化;低秩
随着科学技术的发展,海量数据在带给人们各种便利的同时,也给数据分析和处理带来了极大的困难。如何有效采集和处理高维数据,成为信号处理领域一个亟待解决的问题。2006年,Donoho D L和Candès E等提出一种新颖的信号采样和处理理论,即压缩感知(Compressive Sensing)理论[1-3]。该理论将信号采样和压缩合并进行,提高了信号采集、信息处理能力,突破了香农-奈奎斯特采样定理的瓶颈,大大缓解了数据采集、存储、传输和分析的压力。
压缩感知理论指出,当信号在某个变换域下可压缩或稀疏时,通过采集少量的信号非自适应线性投影值,构建数学重构模型并利用重构算法求解,可以较精确地重构原信号。其研究内容主要包括稀疏表示、编码测量和重构算法三方面。稀疏表示是压缩感知理论的先验条件。从正交基、组合正交基、多尺度几何分析再到字典学习的发展,稀疏表示理论愈加丰富。编码测量是压缩感知理论硬件实现的关键,但并非直接测量信号本身,而是经过测量矩阵将其投影到低维空间,并保持信号原本的结构信息。重构算法是压缩感知理论的核心,指利用尽量少的测量值,快速、鲁棒、精确地重构原信号。
一般地,信号重构过程可转化为一个求解最小l0范数的模型。统计学、计算机领域的研究者从组合算法[4]角度解决稀疏信号重构问题,此类方法比压缩感知理论更早地被提出来。考虑到非确定性因素,Ji S等提出了贝叶斯压缩感知模型[5],这类模型构建了压缩感知和机器学习的桥梁,为深层次研究提供了新的思路。通过逐步迭代的方法逼近待重构稀疏信号的支撑集,从而引出一大类匹配追踪算法[6]。考虑到l0范数的高度非凸性属于NP问题,研究者从多个角度入手,提出了多种近似等价的重构模型。目前主流的研究模型是凸优化模型,即采用凸函数代替非凸函数,并采用凸优化的方法求解。Candès E等采用l1范数代替l0范数,提出最小l1范数模型[3],随后又提出了加权的最小l1范数模型[7]。在Candès E等结合二维图像梯度场稀疏性提出全变分模型[3]的基础上,Lou Y等提出了加权全变分模型[8]。Chartrand R等以牺牲计算复杂度为代价,用lp(0 1959年,Hubel等在研究猫的简单细胞感受野时,发现位于主观视觉皮层V1区的细胞能够对视觉信息进行稀疏表示[14]。生物学家指出,哺乳动物的视觉神经系统是一个非常有效的系统,当观察某个特定画面时,只有有限个视觉神经元被激活,即用较少的神经元表现所观察物体的特征,这是其长期进化的结果。随着人们对稀疏表示理论的深入研究,这一理论被广泛应用于信号处理等领域。 定义1稀疏:信号x在变换基Ψ下的变换系数向量Θ=ΨTx,假如对于0 (1) 说明系数向量Θ在某种意义下是稀疏的[1]。如果Θ中只有少数元素是非零的,则称Θ是稀疏的,那么信号x是可压缩或稀疏的。若只有k个非零元素,则称Θ是信号x的k稀疏表示。 需要指出的是,很少有信号是真正稀疏的。当认为某个信号稀疏时,更确切地说,是这个信号可以通过稀疏信号近似表达。传统上,信号稀疏表示主要基于正交基和组合正交基,如傅里叶变换、小波变换等;之后,为解决高维空间数据稀疏表示问题,提出了多尺度几何分析。根据哺乳动物视觉神经系统接收场的特性,Kondo S提出了更为有效的冗余字典学习[15]。目前,冗余字典的设计和学习是研究的热点和难点。字典可以有效表示信号中的阶跃、纹理、振荡等高维特征信息,其原子不再是单一的基函数,而是通过构造和学习的冗余原子库,增加原子的个数,提高变换系数的冗余性,来增强逼近信号的灵活性,进而提高复杂信号的稀疏表示能力。其中具有非零系数的原子体现了信号的主要结构及特征信息。更形象地说,利用字典中的原子库,采用线性组合方式,可“拼”出最逼近原图像的图像。当然,这个拼图游戏相当复杂。 测量矩阵是压缩感知理论能否成功实现的关键。如果原始信号充分稀疏并且测量值是精确的,则某些条件可以确保重构解是唯一的。这些条件(如零空间性质或约束等距条件等)保证了存在多种矩阵满足压缩感知的要求,如二值随机矩阵、局部傅里叶矩阵、随机Toeplitz矩阵等。 定义2零空间性质:对于矩阵Φ,如果对于非零向量h和所有|S|≤K的坐标集合S⊂{1,2,…,n}都满足: ‖hs‖1<‖hsc‖1 (2) 则Φ满足K阶零空间性质(NullSpaceProperty)[16]。其中:h∈N(Φ){0},N(Φ)表示矩阵Φ的零空间;S={i|xi≠0};Sc={i|xi=0},表示S的余集。 零空间特性表明属于矩阵Φ的零空间向量的非零元素应该是均匀分布的,不会集中在任意K个元素中。K阶零空间特性确保测量矩阵不会出现歧义,即如果Φx=Φx′,则必有x=x′或x≈x′。 当信号真正稀疏时,矩阵的零空间性质足以完整描述在什么条件下才可以重构原始信号。然而,对于近似稀疏信号,需要对矩阵引入一些更为严格的条件,以确保零空间N(Φ)中既不包含稀疏的向量,也不包含近似稀疏的向量。更为严格的条件是约束等距条件(RestrictedIsometryProperty,RIP)。 定义3约束等距条件(RIP):如果存在δK∈(0,1),使得: (3) 对所有的x∈∑K{x:‖x‖0≤K}都成立,则称矩阵Φ满足K阶约束等距特性[17]。其中,δK称为矩阵Φ的约束等距常数。 重构算法是压缩感知模型求解的保证,需要考虑多种因素,如少量的测量值、测量噪声和模型噪声以及重构稳定性等。大量研究表明,重构算法和模型设计多种多样,不同的算法和模型在运算时间、重构精度和稳定性等方面都有各自的特点。 3.1组合算法 组合算法由统计学、计算机科学领域的研究者开发,用于解决稀疏信号重构问题[4]。其本质思想是针对信号进行高度结构化采样,由群测试快速获得信号的支撑集。组合算法主要包括稀疏傅里叶描述法、链追踪等。组合算法需要的测量次数较少,但是没有给出确定性测量矩阵的约束条件,这为新的测量矩阵的提出带来了困难。 3.2贝叶斯模型 (4) 贝叶斯模型提供了一个可以将压缩感知和机器学习连接起来的桥梁。这一思想为更多类型的信号重构算法及模型研究提供了一些有益思路。 3.3匹配追踪算法 匹配追踪算法又称贪婪算法,其基本思想是通过逐步迭代来逼近待重构稀疏信号的支撑集[7]。该算法的种类有很多,其中,匹配追踪(MP)算法、正交匹配追踪(OMP)算法能够以极大的概率重构原信号,但是缺乏相应重构正确性的保证。随后改进的算法有逐步匹配追踪(StOMP)、子空间追踪(SP)、压缩匹配追踪(CoOMP)和正则匹配追踪(ROMP)等,在一定程度上兼顾重构的通用性和复杂性,并提供了理论支撑。对于低维度的小尺度信号重构,贪婪算法的速度快,但是对于含噪声的大尺度重构问题,该算法不具有鲁棒性。 3.4凸优化模型 目前,在压缩感知问题求解中应用最多的是凸优化模型。其基本思想是采用凸函数代替l0范数,并利用凸优化的方法求解。假设J(x)是凸的且促进稀疏性的目标函数,在信号x稀疏性的约束下,求解J(x),使其很小。这类模型是在N空间中一个凸集中优化未知变量x的凸函数J(x)。 基于信号的稀疏性,压缩感知理论从M个测量值y=Φx中重构出原始稀疏信号x∈£N,其中,Φ∈£M×N(M (5) 其中‖·‖0表示零范数,是指非零元素的个数。由于l0范数的非凸性,不易求解,因此研究者将该模型转化为易于求解的重构模型,大致有以下四类。 3.4.1lp重构模型 当p=1时,CandèsE等[3]采用l1范数代替原来的l0范数,将重构模型重写为: (6) 式(6)相应的线性规划问题被称为基追踪。为进一步减小噪声对模型的影响,CandèsE等[7]提出了加权最小l1模型,即: (7) 对于0 (8) 3.4.2全变分重构模型 相对于一维信号重构的最小l1范数模型,考虑二维自然图像,Candès E等[3]利用图像离散梯度的稀疏性,提出了更适合自然图像重构的最小全变分模型,即: minTV(x),s.t.y=Φx (9) 然而,对于边缘纹理信息丰富的区域,其梯度并非1-稀疏,单一的全变分正则项效果并不理想,会产生阶梯效应。针对这种非稀疏的梯度向量,结合各向同性与各向异性,LouY等[8]提出了加权的全变分模型,即: (10) 3.4.3平滑l0范数重构模型 (11) 3.4.4低秩重构模型 图像信息包含了大量的自相关结构,具有高度结构化的稀疏性和低秩性。利用这种非局部相似特性,Dong W等[12-13]提出了非局部低秩重构模型: (12) 其中:X=L+W;L是低秩矩阵;W是高斯噪声矩阵;X是按照聚类思想将图像分块后生成的数据矩阵,用于体现图像的自相关结构。文献[13]采用行列式代替秩,rank(L)=log det(L+εI)(ε是很小的正常数,I是单位矩阵),以避免矩阵行列式为零。模型(12)可重写为: (13) 其中,η、λ均是平衡低秩项和保真项的正参数。 凸优化模型有较强的重构正确性,所需观测的次数较少,但其最大的缺点在于重建速度慢,对于大尺度的重构问题实现困难。因此,研究对测量值要求较少、计算复杂度低、适用大尺度且稳健的重构算法及模型,仍然是压缩感知的关键问题。 压缩感知理论为许多领域带来了革新,在计算机科学、电子工程和信号处理等领域具有广阔的应用前景。 成像是一个传统的信号处理领域,图像在整个数字信号处理领域占有举足轻重的地位,压缩感知理论在成像领域得到了极大的认可。RICE大学成功研制的单像素相机[20]成像灵活,光敏二极管量子效率达90%,能够极大地降低图像失真和噪声,为低像素相机拍摄高质量图像提供了可能。激光雷达[21]取消了机械扫描装置,可避免直接对原始信号的采样,减轻构建地面三维模型时数据处理的压力,增加载荷灵活性。国内的相关研究也在积极进行中。医学成像,尤其是核磁共振成像[22],利用MR图像在小波域的稀疏性和空间域的变分约束,通过高度欠采样数据重构原始图像,将压缩感知理论成功应用于心脏成像、脑成像和快速三维血管造影等,大大提高了成像速度。 此外,压缩感知理论还可应用于模拟数字转换、生物传感、稀疏误差纠错、信号检测和分类以及地球物理数据分析等众多领域。最新研究表明,基于自然成像的压缩感知模型更具有实用价值[23]。随着现代通信技术的飞速发展,压缩感知理论必将大放光彩。 压缩感知理论的提出不仅丰富了信号采样和处理理论,也为其他相关领域的研究提供了新思路。2006年至今,经过十年的研究发展,压缩感知理论框架不断完善。但是,不可否认的是压缩感知理论不具有普适性,如对于随机信号或噪声信号等非结构信号,压缩感知理论仍然存在不能克服的局限性。 压缩感知理论具有旺盛的生命力,发展日新月异,对应用数学、电子光学工程、信号处理等领域将产生重要影响。今后的研究方向主要有以下几个方面: (1)设计性能更好的字典。稀疏字典适合人类视觉神经系统,可充分利用图像的先验信息,确保稀疏性,在减少测量的同时保证重构精度。 (2)测量矩阵的构造和优化。测量矩阵与稀疏字典密切相关,应统筹考虑,更重要的是满足采样成本低、存储矩阵小等硬件易实现的特性要求。 (3)低秩流形符合图像的本征结构。结构化稀疏有着优异的重构效果,低秩流形和结构化字典相结合,重构图像将具有更丰富的结构信息。 [1]DonohoDL.CompressedSensing[J].IEEETransactionsonInformationTheory, 2006, 52(4):1289-1306. [2]CandèsE.CompressiveSampling[C]//ProceedingsofInternationalCongressofMathematiciansMadrid.Spain:EuropeanMathematicalSocietyPublishingHouse, 2006:1433-1452. [3]CandèsE,RombergJ,TaoT.RobustUncertaintyPrinciples:ExactSignalReconstructionfromHighlyIncompleteFrequencyInformation[J].IEEETransactionsonInformationTheory, 2006, 52(2):489-509. [4]GilbertAC,GuhaS,IndykP,etal.Near-optimalSparseFourierRepresentationsViaSampling[C]//Proceedingson34thAnnualACMSymposiumonTheoryofComputing.Canada:ACM, 2012:152-161. [5]JiS,XueY,CarinL.BayesianCompressiveSensing[J].IEEETransactionsonSignalProcessing, 2008, 56(6):2346-2356. [6]方红, 杨海蓉. 贪婪算法与压缩感知理论[J]. 自动化学报, 2011, 37(12):1413-1421. [7]CandèsE,BraunN,WakinM.SparseSignalandImageRecoveryfromCompressiveSamples[C]//Proceedingsof4thIEEEInternationalSymposiumonBiomedicalImaging:fromNanotoMacro.Washington:IEEEE, 2007:976-979. [8]LouY,YinP,HeQ,etal.ComputingSparseRepresentationinaHighlyCoherentDictionaryBasedonDifferenceofL1andL2 [J].JournalofScientificComputing, 2015, 64(1):178-196. [9]ChartrandR.ExactReconstructionofSparseSignalsViaNonconvexMinimization[J].IEEESignalProcessingLetters, 2007, 14(10):707-710. [10]MohimaniH,BabaiezadehM,JuttenC.AFastApproachforOvercompleteSparseDecompositionBasedonSmoothedL0Norm[J].IEEETransactionsonSignalProcessing, 2009, 57(1):289-301. [11]MairalJ,BachF,PonceJ,etal.Non-localSparseModelsforImageRestoration[J].IEEEInternationalConferenceonComputerVision, 2009,30(2):2272 - 2279. [12]DongW,LiX,ZhangL,etal.Sparsity-basedImageDenoisingViaDictionaryLearningandStructuralClustering[J].IEEEConferenceonComputerVision&PatternRecognition,2011,42(7):457-464. [13]DongW,ShiG,LiX,etal.CompressiveSensingViaNonlocalLow-rankRegularization[J].IEEETransactionsonImageProcessingaPublicationoftheIEEESignalProcessingSociety, 2014, 23(8):3618-3632. [14]HubelDH,WieselTN.ReceptiveFieldsofSingleNeuronsintheCat’sStriateCortex[J].JournalofPhysiology, 1959, 148(3):574-591. [15]KondoS.CompressedSensingandRedundantDictionaries[J].InformationTheoryIEEETransactionson, 2008, 54(5):2210-2219. [6]文再文,印卧涛,刘歆,等.压缩感知和稀疏优化简介[J].运筹学学报, 2012, 16(3):49-64. [17]MoQ,LiS.NewBoundsontheRestrictedIsometryConstant[J].Applied&ComputationalHarmonicAnalysis, 2011, 31(3):460-468. [18]BaraniukR,DavenportM,DevoreR,etal.ASimpleProoftheRestrictedIsometryforRandomMatrices[J].ConstructiveApproximation, 2015, 28(3):253-263. [19]李春雷, 高广帅, 刘洲峰,等. 基于L0范数视觉显著性的织物疵点检测算法研究[J]. 中原工学院学报, 2015,26(6):1-5. [20]DuarteMF,DavenportMA,TakbarD,etal.Single-pixelImagingViaCompressiveSampling[J].IEEESignalProcessingMagazine, 2008, 25(2):83-91. [21]HowlandGA,DixonPB,HowellJC.Photon-countingCompressiveSensingLaserRadarfor3DImaging.[J].AppliedOptics, 2011, 50(31):5917-5920. [22]AkakayaM,BashaTA,GodduB,etal.Low-dimensional-structureSelf-learningandThresholding:RegularizationBeyondCompressedSensingforMRIReconstruction[J].MagneticResonanceinMedicineOfficialJournaloftheSocietyofMagneticResonanceinMedicine, 2011, 66(3):756-767. [23]LiutkusA,MartinaD,PopoffS,etal.ImagingwithNature:CompressiveImagingUsingaMultiplyScatteringMedium[J].ScientificReports, 2013, 4(4):5552. (责任编辑:王长通) The Review of Image Reconstruction in Compressive Sensing SONG Chang-ming, HUI Qing-lei (Zhongyuan University of Technology, Zhengzhou 450007,China) In this paper, compressive sensing is systematically studied from the sparse representation, compressive measurement and reconstruction algorithm, and then the theoretical frame and the latest developments of the image reconstruction model are introduced in detail based on probability and convex optimization etc. Some further research directions is put forward from dictionary learning and low-rank represent. compressive sensing; image reconstruction; convex optimization; low rank 2016-05-26 河南省基础与前沿技术研究项目(152300410226);河南省高等学校重点科研项目(15A110045) 宋长明(1965-),男,河南郑州人,教授,博士,主要研究方向为偏微分方程及其应用。 1671-6906(2016)04-0080-05 TN911.7 A 10.3969/j.issn.1671-6906.2016.04.0171 稀疏表示
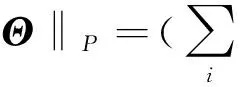
2 测量矩阵


3 重构算法与模型











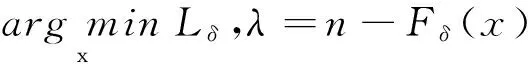


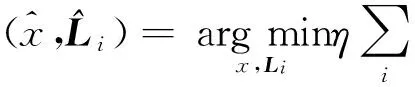
4 压缩成像应用
5 结 语
