带有避碰机制的2阶非线性多智能体系统包围编队研究

曹昊哲，吴炎烜，周峰，王正杰

（北京理工大学机电学院，北京100081）

带有避碰机制的2阶非线性多智能体系统包围编队研究

曹昊哲，吴炎烜，周峰，王正杰

（北京理工大学机电学院，北京100081）

当前关于包围编队的研究没有考虑一定条件下跟随者之间可能出现的碰撞问题。基于图论、矩阵分析、非线性分析，研究带有避碰机制的2阶非线性多智能体系统包围编队问题，分别设计了带有避碰机制的静态和自适应包围编队协议，并结合李雅普诺夫分析方法得到包围协议稳定的充分条件。通过仿真实验验证包围编队协议的有效性。研究结果表明：协议可使跟随者的运动轨迹最终趋向以所有领导者运动轨迹张成凸包的有限半径范围内，同时所有跟随者之间距离均始终大于安全距离。

兵器科学与技术；一致性问题；包围控制；避碰；多智能体系统

0　引言

近年来，多智能体系统的编队问题得到了广泛研究和应用［1］。这里所述智能体是指具有自主控制能力、计算能力的物理对象，例如:无人机、无人车、无人潜航器等。当前多智能体系统编队算法已有很多种，例如最初传统的基于PID控制的编队［2］，该方法的典型特点是需要提前规划好队形，然后每个智能体根据队形来确定相邻节点并发送和接受状态信息。这种算法适用于智能体数量少、编队松散的情况，当智能体数量很多、编队密集时，算法难以扩展和应用；进而，有学者提出基于透光性协议的编队［3］，这种方法易扩展，适用于密集编队，但很难进行稳定性分析，与此类似的还有基于蚁群、遗传等启发式算法的编队［4］，这些算法虽然易于扩展但均难以进行稳定性分析。由于在很多编队问题中，多智能体都需要靠保持速度、方向一致来维持队形，这便产生了所谓的一致性理论，很多学者研究了基于一致性理论的编队［5］，这种基于一致性理论的算法是分布式的，具有良好的扩展性，同时又采用严谨的数学模型来描述，而且可以进行稳定性分析，因此有关一致性问题现已成为当前复杂系统、协同控制等研究领域的重要研究方向。

一致性算法来源于编队，但其应用并不仅限于编队。例如传感器网络在监视目标时需要各个节点对目标信息保持一致，此时就可对网络中每个传感器节点应用一致性算法。又如，在群水下航行器网络中，需要协同跟踪某一目标，但无法保证所有航行器都可以获得目标信息，此时可对网络中航行器应用一致性算法［6］。诸如此类的一致性算法应用还有很多，应用领域广泛。一致性问题分类方式多样，根据网络是否有领导者，一致性问题分两种，即无领导者的一致性［7］以及带有一个或多个领导者的一致性。其中，对于单个领导者的情形，所有跟随者的状态均会收敛至领导者的状态，这种情形也称为一致性跟踪［8］。对于多个领导者的情形，亦有其独特优势，例如一群智能体向某个目标运动，只需部分智能体安装导航、环境感知等传感器，这部分智能体即是领导者，它们拥有较强的运动能力，可精确导航并能探测环境中的障碍物，其他智能体只需聚集在这些领导者所形成的安全区域内并跟随领导者运动，这就是所谓的包围控制。

综上所述可以看出，包围控制不但可以因传感器数量减少而节省成本，从而更具实际应用价值，而且又不会影响包围效果，所以包围控制在近些年获得了广泛研究。在文献［9］研究了多个刚体在无向通信拓扑下的姿态包围控制问题。文献［10］研究了1阶和2阶多智能体系统在有向通信拓扑下的包围控制问题。文献［11］研究了随机切换有向通信拓扑下的包围控制。文献［12］研究了多个拉格朗日系统的包围控制问题。文献［13］提出一种利用相邻节点控制输入的包围控制协议。文献［14］研究了异构多智能体系统的包围控制问题。文献［15］研究了2阶非线性多智能体系统的包围控制问题。文献［16-17］研究了一般动力学多智能体系统的包围控制问题。文献［18］研究领导者控制输入时变情形下的一般动力学多智能体系统的包围控制问题。文献［19］研究了带有不确定项的一般动力学多智能体系统的鲁棒包围控制问题。文献［20］研究了带有通信噪声条件下的1阶积分器网络包围控制问题。文献［21］研究了带有通信延迟的包围控制问题。

包围协议会使跟随者趋向于由所有领导者状态张成的凸包，每个跟随者趋向的凸包权重值由通信拓扑结构决定，由于通信拓扑结构的任意性会使部分跟随者趋向的凸包相近或一样，应用在编队控制中则会导致跟随者相互碰撞，而综上可见，目前对包围编队的避碰问题讨论甚少。文献［22］研究了拉格朗日系统的包围编队问题，只是提到在拉格朗日系统前提下的避碰情况，然而实际的物理系统更多的是具有2阶非线性动力学形式，并非拉格朗日系统。因此本文研究2阶非线性多智能体系统的包围编队控制，设计了一个带有避碰机制的包围编队协议，使得各个跟随者的位置聚集在以所有领导者位置所张成凸包的有限半径范围内，各个跟随者的速度趋向于所有领导者速度所张成的凸包。结合李雅普诺夫稳定性分析方法研究了各个领导者速度任意变化情形下包围编队协议的稳定性。

1　问题描述

一个带有权重的有向图由G=（V，E，A）表示，其中V=（vi，i=1，2，…，N）表示图中有限点集，E⊆V×V表示图的边集，A=（aij）∈RN×N表示图的邻接矩阵。L=（lij）∈RN×N表示图的拉普拉斯矩阵。关于图论中各个概念的详细定义见参考文献［23］。

假设有一个多智能体系统由N个节点组成，序号1，2，…，M表示跟随者，序号M+1，M+2，…，N表示领导者。F=｛1，2，…，M｝表示跟随者集合，R=｛M+1，M+2，…，N｝表示领导者集合。N个节点之间的通信图用Glf表示，^L∈RN×N是同Glf相关的拉普拉斯矩阵，跟随者之间的通信图用G表示，L∈RM×M是同G相关的拉普拉斯矩阵。这里假设多智能体系统通信拓扑的变化规律满足假设1.

假设1 跟随者之间的通信图G是连通的，且

由于领导者不接收任何跟随者的信息，因此^L可划分为每个领导者至少是一个跟随者的邻接点。

为研究问题方便，引入信息交换矩阵的定义:

定义1（信息交换矩阵） 令H=L+B，H∈RM×M是信息交换矩阵，其中，B=diag［b1，b2，…，

式中:H是信息交换矩阵。

引理1［9］若假设1成立，则是一个非负矩阵，且每一行的行和等于1.

定义2（凸包） 有一个集合K⊂Rn，如果对于任意的x、y∈K满足（1-α）x+αy∈K，α∈［0，1］，则称该集合为凸包。一个有限点集x1，x2，…，xN∈ Rn的凸包用来表示，具体定义为

由（1）式可知，当部分跟随者所趋向的凸包相近或相同时会产生碰撞，因此这部分跟随者不能直接趋向凸包，而是趋向凸包附近，同时跟随者之间保持一定安全距离以避免碰撞。这意味着:

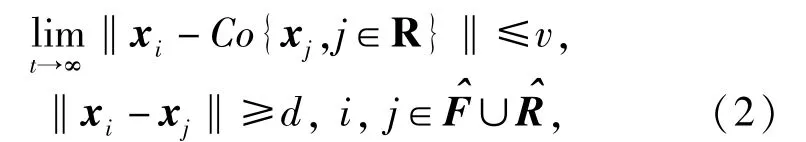
式中:v是正的常数；d表示安全距离；^F⊆F表示所趋向的凸包相近或相同的那部分跟随者；^R⊆R表示与跟随者所趋向的凸包相近的那部分领导者。

2　包围编队协议及稳定性分析

2.1静态包围编队协议

2阶积分器是2阶非线性动力学方程的特例，很多智能体的动力学模型都可以通过输入输出线性化的方式简化为2阶积分器动力学方程［24-25］，但本文均是以一般性的2阶非线性动力学方程来描述，因而讨论的是更具一般性的物理对象编队情形。

每个跟随者的动力学方程为

式中:xi∈Rn和vi∈Rn分别表示第i个跟随者的位置和速度；ui∈Rn是其相应的输入；f:Rn×Rn×R→Rn是连续可微的向量函数。

每个领导者的动力学方程为

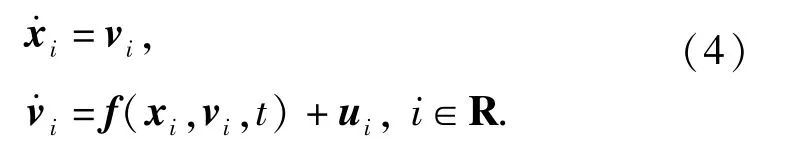
领导者的运动独立于跟随者，并做任意变速运动，因此ui是个时变函数，这里假设各个领导者的速度相同，因此由领导者构成的队形保持不变。假设领导者的非线性动力学模型与跟随者的一样，并且这些非线性动力学模型满足以下假设:

假设2 给定有限数量的非负常数η1，η2，…，存在两个非负的常数ρ1和 ρ2，使得非线性函数f 满足

若N-M=1，即多智能体系统只有一个领导者，则假设2就是很多非线性系统均满足的利普希茨条件。若N-M＞1，即多智能体系统有多个领导者，则只有部分非线性系统满足假设2，选取其中某一种，例如:

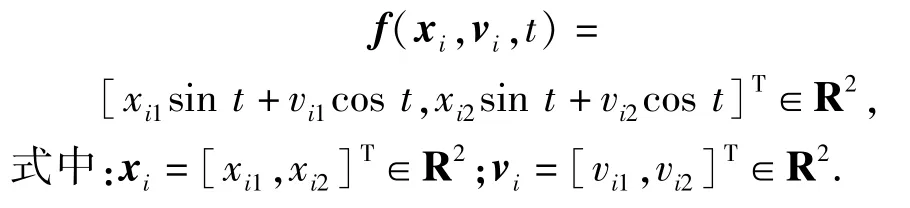
下面介绍势函数的定义，将用于包围编队协议。

定义3（势函数） 势函数Vij是关于‖xi-xj‖的可微、非负函数，并满足以下条件:

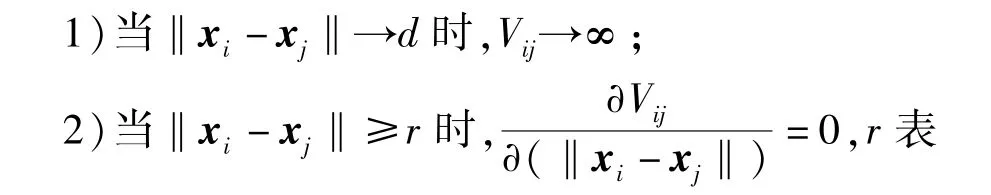
示感知距离，即开始执行避碰机制的距离，r＞d.

引理2［22］对于定义3中的势函数Vij满足

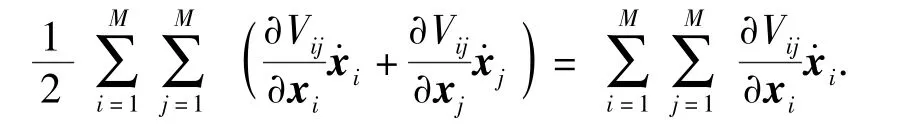
为各个跟随者设计以下静态包围编队协议:

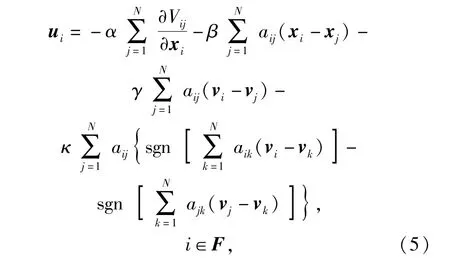
式中:aij（j=1，2，…，N）表示邻接矩阵元素；α、β、γ、κ是正的常数；sgn（·）表示对向量各项做符号运算的函数。

包围协议（5）式由3部分组成:第1部分是协议中第1项，作用是防止碰撞，即让跟随者之间以及跟随者与领导者之间的距离大于安全距离；第2部分是协议中第2项，作用是让每个跟随者趋向各自位置凸包；第3部分是协议中后面几项，作用是让每个跟随者趋向各自速度凸包，协议中非线性项的作用是为了抵消非线性动力学的影响。

再令

多智能体系统（3）式、（4）式、（5）式可写成闭环动力学形式为

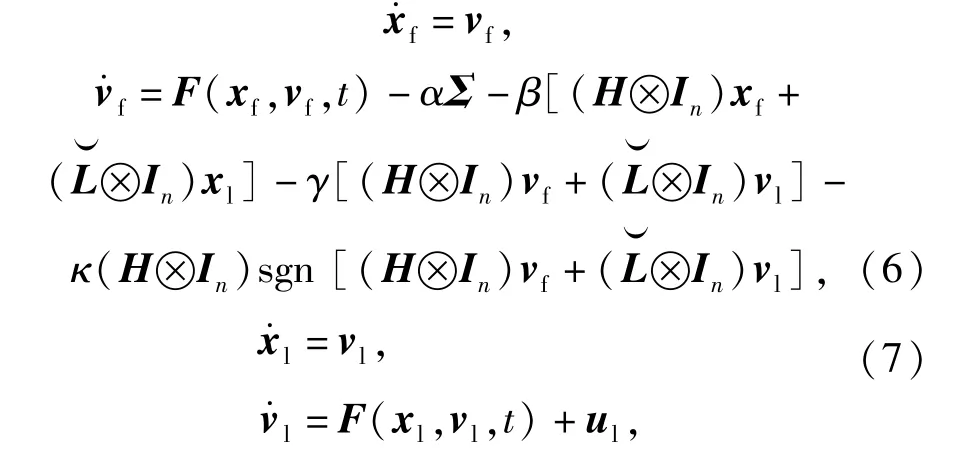
式中:In为n阶单位对角矩阵。

对于多智能体系统（3）式、（4）式和包围编队协议（5）式，得出以下结论:

定理1 对于2阶多智能体系统（3）式和（4）式，若通信拓扑满足假设1，非线性动力学满足假设2，且包围编队协议（5）式中的参数满足条件κ≥

令初始时刻系统中所有节点间距离均大于安全距离，则在协议（5）式的作用下，所有跟随者的位置趋向由所有领导者位置构成凸包的有限半径范围内，且跟随者之间以及跟随者与领导者之间均大于安全距离，跟随者的速度趋向由所有领导者速度构成的凸包。σ1、σ2、σ3和函数V在后文定义，V（0）是李雅普诺夫函数V初始时刻的值。

由上所述可以看出，由于V（0）中包含初始位置、初始速度等信息，所以κ值的确定与这些信息紧密相关。

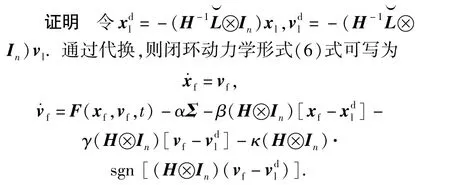
构造李雅普诺夫函数

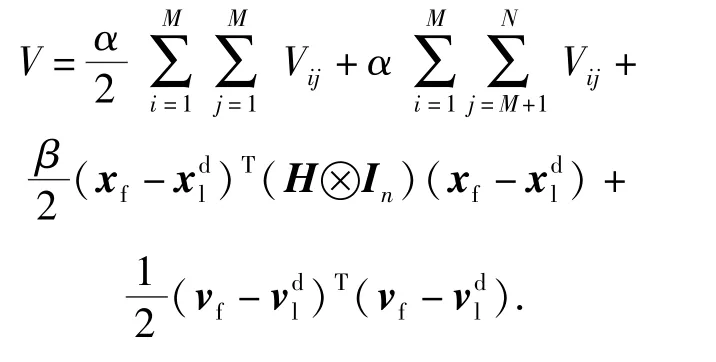
将V沿着系统（6）式的轨线求导可得

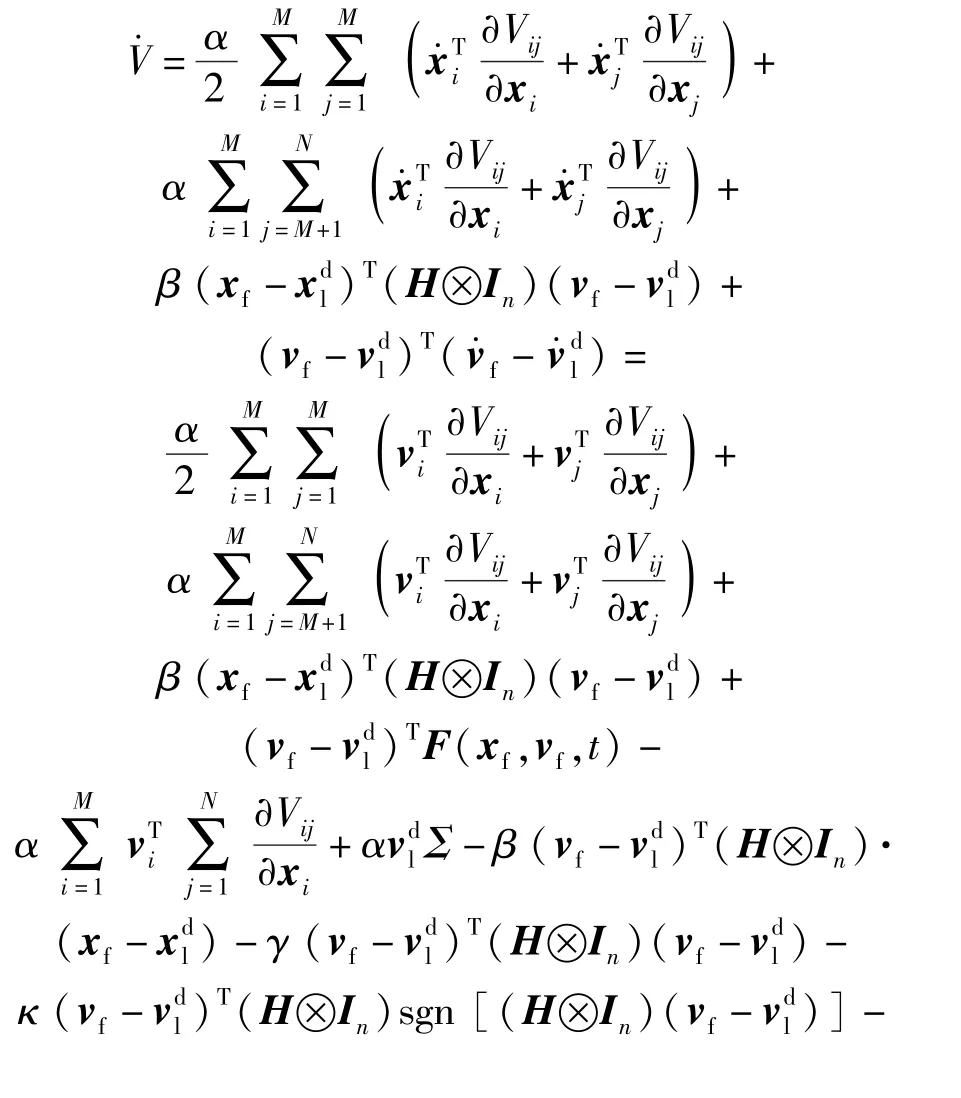
结合引理2以及各个领导者速度均相同这一假设可得

因此（8）式可变为

式中:λmin（·）表示矩阵最小特征值。则由（12）式可得

根据Barbalat引理，由（13）式可知，随着时间t→∞，vf-vdl→0，即每个跟随者的速度趋向于各自的速度凸包。从（10）式还可看出李雅普诺夫函数V是非递增函数，因此对于所有t≥0，V（t）≤V（0），所

2.2自适应包围编队协议

2.1节研究了静态包围编队协议，协议中参数κ的确定需要了解很多全局信息，例如需要知道初始位置和速度、信息交换矩阵、非线性动力学参数以及领导者控制输入上界，很多时候这些全局信息的确定也非常麻烦。因此设计一个自适应包围编队协议，使参数κ通过自适应的方式来确定，且不需要了解任何全局信息。

为各个跟随者设计下面的自适应包围编队协议:

式中:ci表示各个跟随者的时变增益。

多智能体系统（3）式、（4）式、（14）式可写成闭环动力学形式:

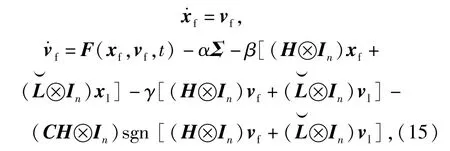
式中:C=diag（c1，c2，…，cM）.

对于多智能体系统（3）式、（4）式和包围编队协议（14）式，得出以下结论:

定理2 对于2阶多智能体系统（3）式和（4）式，若通信拓扑满足假设1，非线性动力学满足假设2，令初始时刻系统中所有节点间距离均大于安全距离，则在协议（14）式的作用下，系统中所有跟随者的位置趋向由所有领导者位置构成凸包的有限半径范围内，且跟随者之间以及跟随者与领导者之间均大于安全距离，跟随者的速度趋向由所有领导者速度构成的凸包。

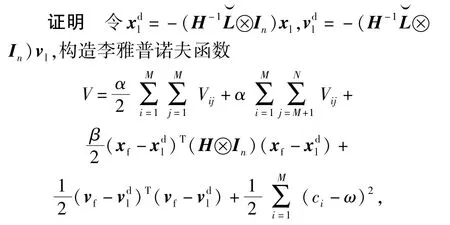
式中:ω是足够大的正常数。

将V沿着系统（15）式的轨线求导可得

各个跟随者的时变增益ci是个递增的变量，2.2节中的李雅普诺夫函数又是非递增的函数，因此时变增益ci有上界，并趋向一个稳定的值。

类似文献［26］中的讨论，本文多智能体系统的信息交换图分为感知图和通信图，从前面的分析可看出感知图对应的拓扑是时变的，包围编队协议中的第1项就是基于感知图，该项的作用是防止智能体之间的碰撞。通信图满足假设1，其对应的拓扑是固定的，包围编队协议中的其他项基于通信图，这些项的作用是让每个跟随者趋向各自对应的位置和速度凸包。

3　仿真结果

这一部分对包围编队协议（14）式进行数值仿真来验证其有效性。考虑一个2阶多智能体系统由3个领导者和4个跟随者组成，其通信图对应的邻接矩阵如下:

各个智能体的非线性动力学具有如下形式:

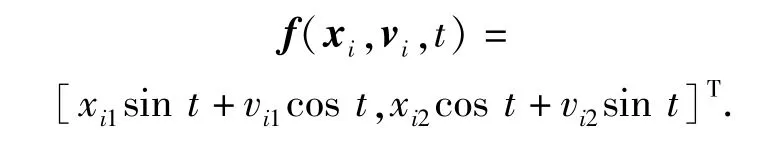
各个跟随者的初始位置是:x1=［0m，30m］T，x2=［30m，30m］T，x3=［30m，0m］T，x4=［0m，0m］T，初始速度均为0m/s.假设各个领导者采用一定的控制率使其各自保持在如下位置:x5=［60m，30m］T，x6=［80m，15m］T，x7=［60m，0m］T.碰撞安全距离d=8 m，感知距离r= 10m.控制输入协议（14）式中参数α、β、γ选取α= 1，β=15，γ=0.05.

势函数的具体形式有很多，这里采用如下形式:

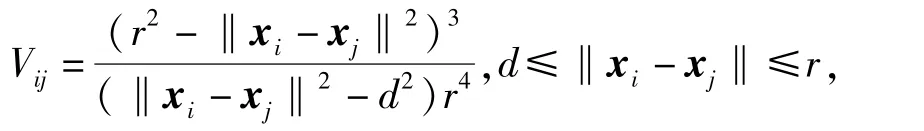
容易验证，其满足定义3.

图1是采用文献［15］的不含避碰机制的包围编队协议仿真结果。其中，黑色三角形的3个顶点分别表示3个领导者的位置，4条彩色轨迹分别表示4个跟随者的运动轨迹。图2中的彩色轨迹分别对应图1中两两跟随者之间的距离，黑色虚线表示安全距离。从图2中结果可看出，虽然每个跟随者趋向各自位置凸包，但很多跟随者间的距离小于安全距离。

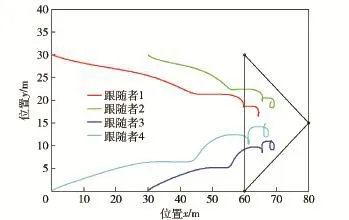
图1 不含避碰机制的包围编队Fig.1 Containment without collision avoidance mechanism

图3是加入避碰机制的包围编队仿真结果，采用的是本文提出的包围编队协议（14）式。其中，黑色三角形与4条彩色轨迹线与图1含义相同，图4中的彩色轨迹线分别对应表示图3中两两跟随者之间的距离，黑色虚线同样表示安全距离。从图4中可看出任意两个跟随者间的距离均大于安全距离，同时所有跟随者分布在各自位置凸包附近。

图2　两两跟随者间的距离Fig.2 Distances among followers

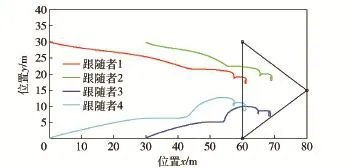
图3　加入避碰机制的包围编队Fig.3 Containment with collision avoidance mechanism

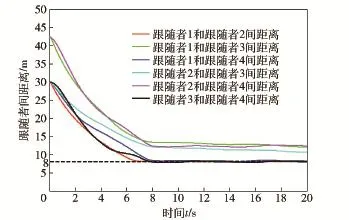
图4　两两跟随者间的距离Fig.4 Distances among followers

本文所提出的包围编队协议对碰撞安全距离和感知距离大小没有特殊限制，理论上只要满足感知距离大于安全距离的逻辑条件即可，具体的取值可根据实际物理对象的约束确定。图5和图6是碰撞安全距离d=20 m，感知距离r=50 m情形下的仿真结果。其中，各个跟随者的初始位置是: x1=［0m，150m］T，x2=［150m，150m］T，x3=［150m，0m］T，x4=［0m，0m］T，初始速度均为0m/s.并且假设对各个领导者采用一定的控制率，使其各自保持在如下位置:x5=［300m，150m］T，x6=［400m，60m］T，x7=［300m，0m］T.

图5　加入避碰机制的包围编队Fig.5 Containment with collision avoidance mechanism

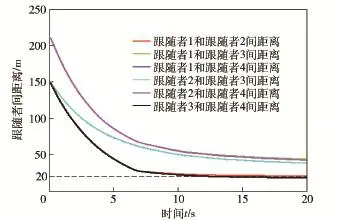
图6　两两跟随者间的距离Fig.6 Distances among followers

本文前述对于领导者采用一定的控制器，使其保持位置固定，但本文所提协议并不限定领导者必须保持位置固定。为了展现编队协议控制能力，图7是在本文所提出的包围编队协议（14）式控制下的领导者运动情形的仿真结果。虚线三角形的顶点，表示领导者的初始位置；实线三角形的顶点，表示领导者的仿真结束位置，3条黑色轨迹分别表示3个领导者的运动轨迹，领导者在x轴和y轴方向上的运动速度均是3 m/s.4条彩色轨迹线分别表示4个跟随者从初始时刻到仿真结束的运动轨迹，初始时刻速度均为0 m/s.领导者与跟随者初始位置如图7所示，这里不再赘述。由图7可见:跟随者的运动轨迹最终趋向领导者轨迹张成的凸包。

图8中彩色线条同前所述，依然表示图7中两两跟随者之间的距离，黑色虚线表示安全距离。从图8中可见，任意两个跟随者间的距离均始终大于安全距离。

4　结论

本文研究了2阶非线性多智能体系统的包围编队问题，基于邻近状态信息分别设计了静态和自适应包围编队协议。对于静态包围编队协议，通过李雅普诺夫分析得到其稳定的充分条件。对于自适应包围编队协议则不需要任何全局信息，是完全分布式的。两种包围编队协议均可使各个跟随者的位置聚集在以所有领导者位置所张成凸包的有限半径范围内，同时所有跟随者之间以及跟随者与领导者之间距离均大于安全距离。数值仿真结果验证了该协议的有效性。

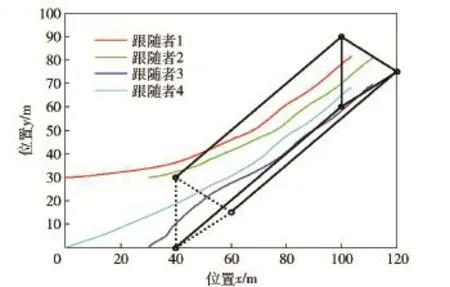
图7　领导者运动情形下加入避碰机制的包围编队Fig.7 Containment with collision avoidance mechanism of moving leaders

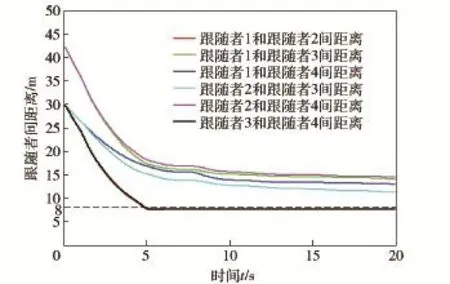
图8　两两跟随者间的距离Fig.8 Distances among followers

（References）

［1］ Oh K K，Park M C，Ahn H.A survey of multi-agent formation control［J］.Automatica，2015，53:424-440.

［2］ 刘小熊，章卫国，王振华，等.无人机自适应编队飞行控制设计与仿真［J］.系统仿真学报，2009，21（5）:1420-1422. LIU Xiao-xiong，ZHANG Wei-guo，WANG Zhen-hua，et al.A-daptive formation flight control design for UAVs［J］.Journal of System Simulation，2009，21（5）:1420-1422.（in Chinese）

［3］ 吴森堂，张杰，杜阳.一种基于透光性假说的飞行器密集自主编队控制方法:中国，201310671331.3［P］.2014-03-12. WU Sen-tang，ZHANG Jie，DU Yang.A dense autonomous forma-tional control method of aircraft based on the translucent hypothesis:China，201310671331.3［P］.2014-03-12.（in Chinese）

［4］ 张邦楚，彭琛，余新荣.基于蚁群优化的多弹协同目标分配算法［J］.弹箭与制导学报，2012，32（4）:69-73. ZHANG Bang-chu，PENG Chen，YU Xin-rong.Cooperative target assignment algorithm of multiple missile based on ant colony optimization［J］.Journal of Projectiles，Rockets，Missiles and Guidance.2012，32（4）:69-73.（in Chinese）

［5］ Olfati-saber R，Fax A，Murry M R.Consensus and cooperation in networked multi-agent systems［J］.Proceedings of IEEE.2007，95（1）:215-233

［6］ 王银涛，严卫生.多自主水下航行器系统一致性编队跟踪控［J］.控制理论与应用，2013，30（3）:379-384. WANG Yin-tao，YAN Wei-sheng.Consensus formation tracking control of multiple autonomous underwater vehicle systems［J］. Control Theory and Applicaions.2013，30（3）:379-384.（in Chinese）

［7］ 薛瑞彬，宋建梅，张民强.具有时延及联合连通拓扑的多飞行器分布式协同编队飞行控制研究［J］.兵工学报，2015，36（3）:492-502. XUE Rui-bin，SONG Jian-mei，ZHANG Min-qiang.Research on distributed multi-vehicle coordinated formation flight control with coupling time-delay and jointly-connected topologies［J］.Acta Armamentarii，2015，36（3）:492-502.（in Chinese）

［8］ 王青，后德龙，李君，等.存在时延和拓扑不确定的多弹分散化协同制导时间一致性分析［J］.兵工学报，2014，35（7）: 982-989. WANG Qing，HOU De-long，LI Jun，et al.Consensus analysis of multi-missile decentralized cooperative guidance time with time-delays and topologies uncertainty［J］.Acta Armamentarii，2014，35（7）:982-989.（in Chinese）

［9］ Meng Z Y，Ren W，You Z.Distributed finite-time attitude containment control for multiple rigid bodies［J］.Automatica，2010，46:2092-2099.

［10］ Liu H Y，XIEGM，Wang L.Necessary and sufficient conditions for containment control of networked multi-agent systems［J］. Automatica，2012，48:1415-1422.

［11］ Lou Y C，Hong Y G.Target containment control of multi-agent systems with random switching interconnection topologies［J］. Automatica，2012，48:879-885.

［12］ Mei J，Ren W，Ma G F.Distributed containment control for Lagrangian networks with parametric uncertainties under a directed graph［J］.Automatica，2012，48:653-659.

［13］ Liu S，Xie L H，Zhang H S.Containment control of multi-agent systems by exploiting the control inputs of neighbors［J］.International Journal of Robust and Nonlinear Control，2013，23（5）: 534-547.

［14］ Zheng Y S，Wang L.Containment control of heterogeneous multiagent systems［J］.International Journal of Control，2014，87（1）:37-41.

［15］ Wang P，Jia Y M.Distributed containment control of second-or-der multi-agent systems with inherent non-linear dynamics［J］. IET Control Theory and Applications，2014，8（4）:277-287.

［16］ Li Z K，Duan Z S，Ren W，et al.Containment control of linear multi-agent systems with multiple leaders of bounded Inputs using distributed continuous controllers［J］.International Journal of Robust and Nonlinear Control，2014，25（13）:2101-2121.

［17］ Ma Q，Miao G Y.Distributed containment control of linear multiagent systems［J］.Neurocomputing，2014，133（10）:399-403.

［18］ Li Z K，Ren W，Liu X D，et al.Distributed containment control of multi-agent systems with general linear dynamics in the presence of multiple leaders［J］.International Journal of Robust and Nonlinear Control，2013，23（5）:534-547.

［19］ Wen G H，Duan Z S，Zhao Y，et al.Robust containment tracking of uncertain linear multi-agent systems:a non-smooth control approach［J］.International Journal of Control，2014，87（12）: 2522-2534.

［20］ LiW Q，Xie L H，Zhang JF.Containment tracking of leader-following multi-agent systems with measurement noise［C］∥32nd Chinese Control Conference.Xi'an，Shaanxi，China:TCCT，2013:7330-7334.

［21］ Liu K E，Xie GM，Wang L.Containment control for second-order multi-agent systems with time-varying delays［J］.Systems and Control Letters.2014，67（7）:24-31.

［22］ Meng Z Y，Lin Z L，Ren W.Leader-follower swarm tracking for networked Lagrange systems［J］.Systems and Control Letters，2012，61（1）:117-126.

［23］ Godsil C，Royle G.Algebraic Graph Theory［M］.NY，US: Springer，2001.

［24］ Ren W.Consensus strategies for cooperative control of vehicle formations［J］.IET Control Theory and Applications，2007，1（2）:505-512.

［25］ LiW.Persistent surveillance for a swarm of micro aerial vehicles by flocking algorithm［J］.Journal of Aerospace Engineering，2015，229（1）:185-194.

［26］ Cao Y C，Ren W.Distributed coordinated tracking with reduced interaction via a variable structure approach［J］.IEEE Transactions on Automatic Control，2012，57（1）:33-48.

Research on Containment Control of Second-order Nonlinear Multi-agent with Collision Avoidance Mechanism

CAO Hao-zhe，WU Yan-xuan，ZHOU Feng，WANG Zheng-jie
（School of Mechatronical Engineering，Beijing Institute of Technology，Beijing 100081）

The containment protocol proposed in the previous researches does not take the collision among followers into consideration under certain conditions.The containment of second-order nonlinear multi-agent system with collision avoidance mechanism around formation is studied based on the graph theory，matrix analysis and nonlinear analysis.The static and adaptive protocols are proposed，respectively.Lyapunov method is used to obtain the sufficient condition for stability of protocols.The simulations are used to verify the effectiveness of the containment control protocols.The protocols can make followers'trajectories finally converge to a finite radius from the convex hull spanned by leaders'trajectories，and keep the distances among followers being more than the safe distances all the time.

ordnance science and technology；consensus problem；containment control；collision avoidance；multi-agent system

V279+.2

A

1000-1093（2016）09-1646-09

10.3969/j.issn.1000-1093.2016.09.014

2015-11-12

北京理工大学基础研究基金项目（20120242009）

曹昊哲（1989—），男，博士研究生。E-mail:horizoncao@163.com；吴炎烜（1981—），男，讲师，博士。E-mail:alexwyx@bit.edu.cn