基于双微楔的高超声速激波与边界层干扰控制研究

董祥瑞，陈耀慧，董刚，刘怡昕

（南京理工大学瞬态物理国家重点实验室，江苏南京290014）

基于双微楔的高超声速激波与边界层干扰控制研究

董祥瑞，陈耀慧，董刚，刘怡昕

（南京理工大学瞬态物理国家重点实验室，江苏南京290014）

高超声速飞行器在流场中通常会伴随激波与边界层干扰（SWBLI），其引发的流动分离将导致进气道性能下降。采用分离涡模型结合有限体积离散方法、自适应网格加密技术，对来流马赫数为7.0流场中SWBLI诱导的流动分离进行数值模拟，并基于边界层流向速度、压力梯度、形状因子、总压损失等参数讨论了不同微楔高度的控制效果，分析双微楔的控制机理。研究结果表明：双微楔产生的两对流向涡对之间的相互诱导促进了各自流向涡对之间的卷吸作用，使得双微楔对分离气泡的消除效果优于单只微楔；流动总压损失系数随着微楔阵列高度的增加呈先减小、后增加的趋势；综合讨论流向涡强度与形状阻力的影响，高度为35％分离气泡厚度的双微楔控制效果最好，分离气泡局部可减小至回流消失，边界层形状因子峰值降低86％，总压损失降低1.9％.

流体力学；高超声速；激波与边界层干扰；微楔涡流发生器；流动分离控制；流向涡

0　引言

在超声速及高超声速内外流场中，飞行器表面突起物所产生的激波与其边界层相互作用所导致的流动分离，对飞行器表面及发动机工作性能产生不良影响:如局部压力、热载荷升高，飞行阻力增加，升力降低，总压损失增加、发动机不启动等。因此，超声速的流动分离及控制技术对超声速及高超声速飞行器的研制与性能优化具有重要意义。

激波与边界层干扰（SWBLI）现象最早发现于1939年，Ferri等［1］在超声速风洞试验中首次观察到机翼后缘附近SWBLI导致的边界层分离现象。近几十年来，国内外学者和研究人员对SWBLI现象及其控制技术进行了大量实验与数值研究。Mailison等［2］在压缩拐角流动的实验中，详细描述了不同来流条件下表面压力与热流密度的分布规律以及分离出现的确定条件。MacCormack［3］首次开展了数值模拟方面的工作，其关于二维及三维压缩拐角诱导的激波与层流边界层相互作用的模拟取得了突破性的进展。Urbin等［4］与Garnier等［5］先后采用大涡模拟（LES）方法对SWBLI展开数值研究，发现LES相比雷诺平均模拟（RANS）方法更能够准确而又高效地完成复杂的激波与边界层的作用过程。目前针对SWBLI现象的控制主要有边界层吹除［6］、抽吸［7］、循环控制［8］、等离子体控制［9］以及涡流发生器（VG）控制［10］等方式，其中，被动VG以其构造简单、安装方便、无需供电、性价比高、控制效率高等优点成为近几年SWBLI控制的研究热点。然而由于传统VG的附加形状阻力对主流产生的强扰动，影响飞行器整体工作效率，各国学者逐渐将研究方向转向高度约为0.1至0.5倍边界层厚度的微型涡流发生器（MVG）。2006年，Anderson等［11］提出一种特殊MVG构型:“micro-ramp”，与传统VG作用相当，且具有低耗费，构型简单，自身稳定性高，附加形状阻力极小等优势，并通过采用响应面模型的实验方法在RANS基础上对马赫数Ma为2.0来流条件下的3种VG:标准微叶片，锥形微叶片和标准微楔进行构型参数优化。此后，Lee等［12］分别利用RANS、LES以及单调集成大涡模拟（MILES）方法进行了超声速条件下微楔的相关研究，得出LES能够更好地模拟瞬时流场；同时比较了BR（基本微楔模型）、HR（微楔高度为BR的50％）和HRD（微楔高度为BR的50％，且尾缘位于初始位置与激波入射点的中心）3种微楔模型的控制效果，发现由于BR模型高度高于边界层超声速区域，导致总压损失的增加以及涡旋的快速脱落。因此，后两种比BR控制效果更好。Sharma等［13］在基于一种新型MVG（开槽楔形块）对来流马赫数为2.5的超声速流场的SWBLI控制研究中指出，这种新型MVG控制效果比标准MVG更好，且适当增加MVG装置高度与槽道直径可以提高其控制效果。近期不少学者集中于各种MVG的尾流结构的研究。Zhang等［14］也提出一种新型MVG:非对称型MVG，并在研究中指出这种构型的MVG可以产生和标准构型具有相同路径、相似耗散和涡量的逆旋流向涡对，同时能够有效减少涡对之间的不利影响。此外，Giepman等［15］研究了不同微楔高度、不同来流马赫数对流动分离控制效果的影响，发现微楔尾流高度、强度、涡核高度随微楔高度的增加呈线性增加趋势，然而分离控制效果随着马赫数的增加而降低。文献［16-17］在激波与涡环结构的相互作用研究中指出，MVG诱导的流向涡与开尔文-赫姆霍兹（K-H）涡对SWBLI的控制均可起到积极作用，然而K-H涡结构比流向涡更稳定，可维持其形状直至穿透激波边界层作用区；不同入口流动条件会对环形结构的形状、涡来源、动量亏损区及流向速度剖面产生至关重要的影响。国内学者闫文辉等［18］应用GAO-YONG可压缩湍流方程组数值模拟了SWBLI现象。薛大文等［19-20］采用LES方法和沉浸边界法，数值模拟了微型三角楔超声速绕流特性与其控制作用下的翼型绕流，揭示了微楔改变超声速流体边界层结构的控制机理。刘刚等［21］利用RANS方法对叶片式VG进行了数值模拟，探讨了VG的安装方式、剖面形状、几何尺度等因素对分离流动控制的影响。

尽管国内外学者对SWBLI控制技术进行了大量的数值与实验研究，如跨声速、超声速条件下主、被动VG的控制机理以及VG诱导的涡系结构与边界层流动特性等，其中来流马赫数处于0.8～3.5之间较为多见。然而有关高超声速（Ma＞5）流场中SWBLI诱导的分离边界层形状因子、总压损失等特性及双微楔控制机理研究的文章鲜有报道。本文采用分离涡模型（DES）、结合有限体积离散方法与自适应网格加密技术（AMR）技术对来流马赫数为7.0流场中SWBLI所诱导的流动分离的微楔控制进行了数值计算。相比Ma＜5的超声速流动，从网格尺度、流场边界条件以及激波发生器等几何模型方面进行了完善。分析了单、双微楔的控制机理，并基于边界层流向速度、压力梯度、形状因子、总压损失等参数讨论了微楔高度对流动分离控制效果的影响。

1　数学模型与数值方法

1.1数学模型

本文暂不考虑局部结构烧蚀，重点研究SWBLI控制机理与控制效果。采用三维可压Navier-Stokes方程为

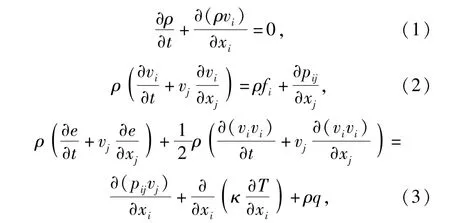
式中:ρ为气体密度；xi、vi与fi分别为3个笛卡尔方向的坐标、速度分量与受力；pij=-pδij+τij为压应力张量和黏性应力张量之和，p为气体压力，τij= λskkδij+2μsij，sij为变形速度对称张量，λ、μ分别为第2黏性系数与动力学黏性系数；κ与T分别为热传导系数和温度；e为单位质量的内能；q为由于辐射等原因在单位时间内传入单位质量的热量。设定气体为理想气体，则有状态方程p=ρRT，R为气体常数。

1.2计算方法

对于大多数分离流动的计算，人们普遍认为LES方法能够获得比RANS更可靠的解。然而LES和直接数值模拟方法（DNS）在复杂外形和高雷诺数（Re＞105）问题中巨大的计算量使其难以在工程中广泛应用［22］。DES方法作为一种RANS/LES耦合的方法，结合LES和RANS的优点，其湍流模型在网格足够密的区域采用LES中的亚格子应力模型，在其他区域采用RANS模型。本文在剪切应力传输（SST）k-ω湍流模型的基础上采用DES方法数值模拟了高超声速（Ma=7）条件下SWBLI诱导的流动分离流场。SST k-ω湍流模型方程为

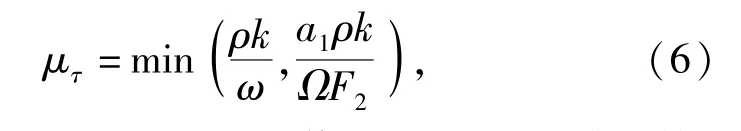
a1为模型常数，Ω为涡量绝对值；F1、F2为开关函数；采用DES模型时，需将湍流尺度lk-ω=k1/2/（β*ω）替换成lDES=min（lk-ω，CDESΔ），其中Δ=max（Δx，Δy，Δz）为网格单元最大边长。当湍流尺度小于Δ时，采用SST两方程模型；当湍流尺度大于Δ时，则采用LES模型。各常数取值如下:CDES=0.78，β*=0.09.将上述数学模型进行无量纲处理并用有限体积法进行离散，对流项采用3阶MUSCL差分格式，时间推进采用3阶精度的龙格-库塔法。

1.3计算模型

本文采取7种不同微楔配置（模型1～模型7）对SWBLI流场进行控制，几何模型参数设定见表1.图1为模型8（无控）流场流向速度等值线分布，无控流场中分离气泡高度δ′=0.6mm.流场计算区域节点数为180×160×80，采用AMR对微楔周边及压力梯度变化较大区域进行了网格加密（见图2），激波发生角α为20°，来流马赫数为7.0.其他几何参数参考Anderson等［11］提出的最佳构型参数设定: Ap=24°，c=7.2h，s=7.5h，xp=15h（见图3），xp为VG尾缘与分离气泡中心的流向距离。

表1　几何模型参数Tab.1 Parameters of geometric model

式中:ρ、k、ω、t、ui、μ分别为密度、湍动能、比耗散率、时间、速度分量、层流黏性系数；σk、σω、Cω、σω2和βω为模式参数；Pk、Pω为湍流生成项［23］；μτ为湍流黏性系数，即

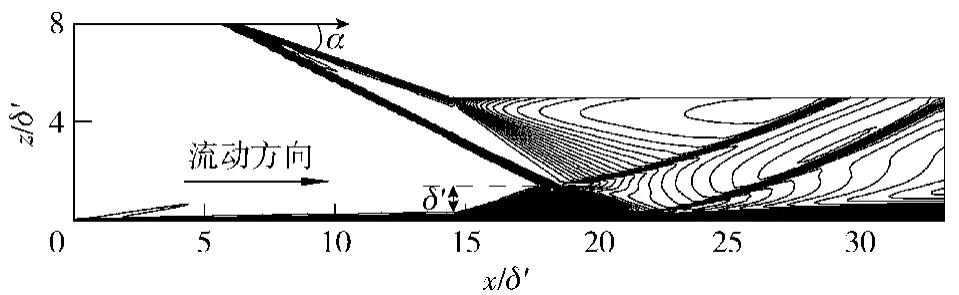
图1　SWBLI现象Fig.1 Shock wave/boundary layer interaction

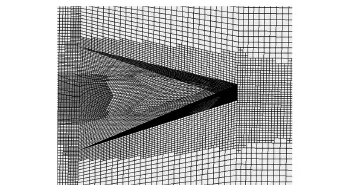
图2　流场自适应网格Fig.2 Adaptive grid of flow field

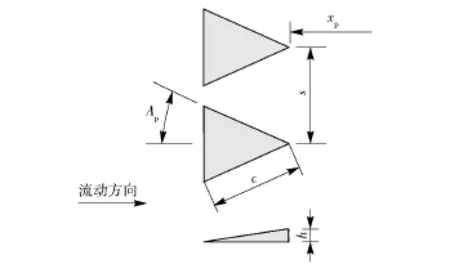
图3　双微楔几何构型Fig.3 Geometric configuration of micro-ramps

1.4数值方法验证

为验证上述数值方法，本文引用美国Lee等［12］的无控流场模型的LES模拟结果及WPAF实验结果进行对比讨论。风洞实验段Ma=3.0，来流压力p∞=7.076×104N/m2，温度T=582.3 K.本文采用DES模拟无控流场模型，且流场几何模型与初始条件、边界条件等均与之一致。图4与图5分别为流场中x/δ*=86.2处的流向速度u与总压p0无量纲值u/u∞、p0/p0∞沿法向的分布，δ*=1.9 mm为边界层位移厚度，其中u∞为入口来流速度，p0∞为入口来流总压。在x/δ*=86.2截面处，其速度分布为未受干扰的边界层流动，对比本文模拟结果和文献［12］的实验与模拟结果，可知二者具有相似性，尤其是速度剖面与文献［12］结果较为吻合；总压分布的模拟结果与文献［12］数据相比有少许亏损，这是由于本文所模拟的无控流场所受入口激波的影响相对较大，总压损失稍有增加，然而此现象并不影响其变化趋势，相似性依然可见，因此可验证该数值方法的可靠性。

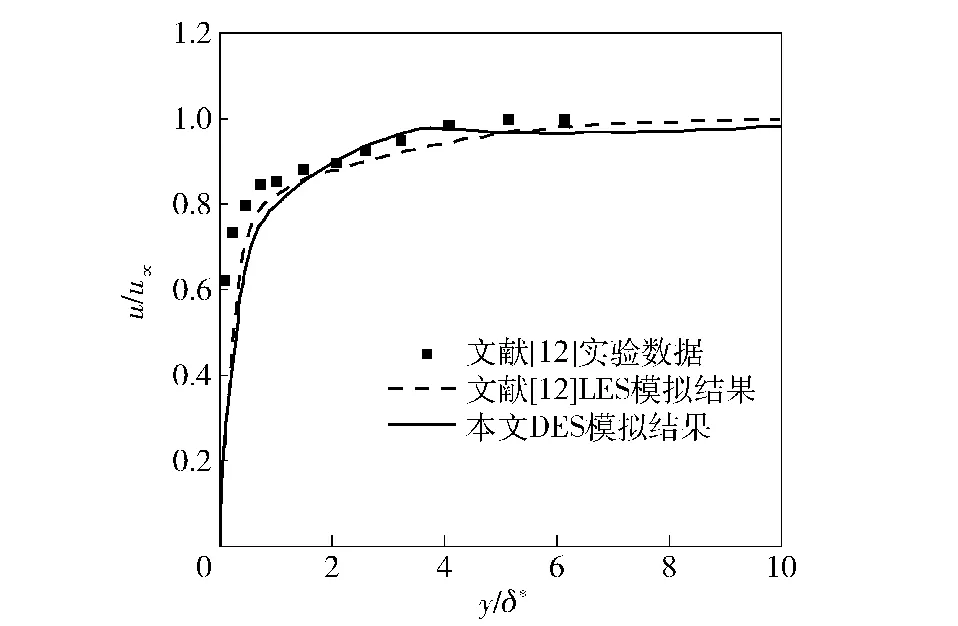
图4　x/δ*=86.2处速度剖面Fig.4 Velocity profiles for x/δ*=86.2

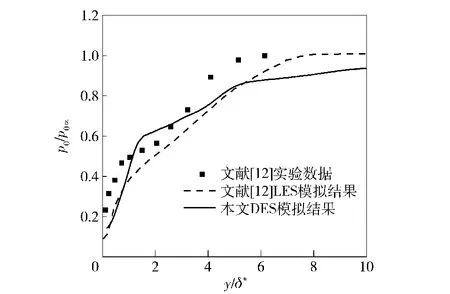
图5　x/δ*=86.2处总压分布Fig.5 Total pressure distribution for x/δ*=86.2

2　结果与分析

2.1单、双微楔控制机理

图6（a）和图6（b）分别为表1中模型1（单微楔）与模型3（双微楔）流场流线与u=0等值面分布，微楔几何尺寸相同。分析图6可知，流经微楔后缘上表面流体沿下游下沉并分流，同时带动附近高能流体向下翻卷；然而流经微楔两侧流体沿下游向对称中心面汇聚，同时带动壁面附近分离气泡内低能流体向上抬升。这两股流体分别经过汇聚与分流等过程相互作用形成一逆旋流向涡对，将分离边界层内低能流体与上方高能流体进行掺混，起到动量交换的作用。图6（a）中的对称面凸起就是低能流体被流向涡对带入边界层上方的结果，且位于该涡对正下方的u=0等值面包裹下的分离气泡向壁面凹陷，再附线向上游缩进，可确定微楔能够有效改善分离气泡的形状。相比单微楔，双微楔下游的分离气泡向下凹陷甚至消失，再附线也沿上游缩进（见图6（b））.此外，图7为模型3下游分离区域表面拓扑结构，由流体流向可得出分离初始位置与再附位置分别位于x/δ′=17与x/δ′=21处，其中，微楔下游的回流流体被破坏并呈现更复杂的三维结构，两对逆旋涡如图7所示。

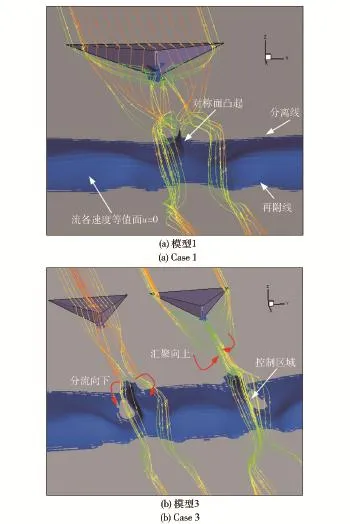
图6　微楔绕流结构与工作机理Fig.6 Flow around micro-ramp and working mechanism

为进一步说明上述双微楔的控制效果优于单微楔的原因，图8给出双微楔后缘诱导的两对流向涡对的运动示意图。分析可得双微楔控制机理:两微楔各自诱导一对流向涡，其旋转方向如图8所示流向涡对1、2与3、4.由于2、3流向涡间隙有限，两涡在边界层上方不断相遇，一同带动附近高速流体向壁面流动，在近壁处相离。这两涡相互诱导使得被带入的高速流体促进了低速流体的卷吸过程，同时也促进了2、3涡与1、4涡对分离气泡内回流的抬升与掺混。由于这一系列促进作用，最终使得两涡对外侧涡（1、4）的卷吸效果优于单微楔诱导的流向涡。

图7　双微楔下游表面拓扑结构（模型3）Fig.7 Downstream surface topology of micro-ramps（Case 3）

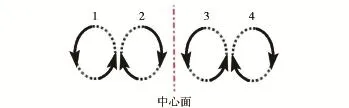
图8　流向涡对运动示意图Fig.8 Motion of streamwise vortex pairs

2.2基于不同双微楔高度控制的边界层特性

图9（a）～图9（f）为表1所列模型2～模型7流场流向速度u=0等值面分布，图9中箭头所示对称中心面与控制面分别为微楔尖端与一对流向涡涡核心展向截面。由图9（a）～图9（f）可知，控制面附近u=0等值面局部凹陷甚至消失。对称中心面附近分离线与再附线稍有前移，这分别是由于微楔后缘自身阻力引起的局部流动黏滞以及流向涡对于卷入其正中心的低速流体的掺混作用。模型2虽然在控制面附近u=0等值面区域减小最多，然而对称中心面处凸起也最明显，说明流场局部分离区域得到控制的同时，微楔自身的附加阻力影响也不容忽视。模型6、模型7由于微楔的h、c较小，所诱导的流向涡强度较弱，尤其两对涡对距离s过小会产生一定负面影响，因此控制效果并不明显。模型3、模型4控制结果最为理想，控制面分离气泡厚度减少甚至消失，对称中心面也没有产生严重影响。

图10（a）～图10（c）为模型2～模型8流场微楔下游流动分离区域附近3个不同流向位置的边界层流向速度剖面（x/δ′=18.3，x/δ′=19.0，x/δ′= 19.8）。其中实线代表模型8无控情况。分析图10可知，模型8边界层底部（z/δ′≤0.4）流体流向速度为负值，速度剖面出现拐点，此时3个流向位置u= 0等值面高度分别为0.15δ′、0.22δ′和0.24δ′.模型2～模型7边界层内速度剖面与模型8相比更饱满，流向速度梯度均有增加，分离边界层内回流速度减小，甚至消失。然而有控流场边界层上方流向速度出现亏损，这是流向涡对边界层上方高能量流体与分离气泡内低能流体的掺混作用的结果。模型3与模型4控制效果最好，3个流向位置的u=0等值面高度分别减小到0δ′，0.01δ′，0.07δ′与0δ′，0.01δ′，0.08δ′，分离区回流厚度局部可减少至回流消失。

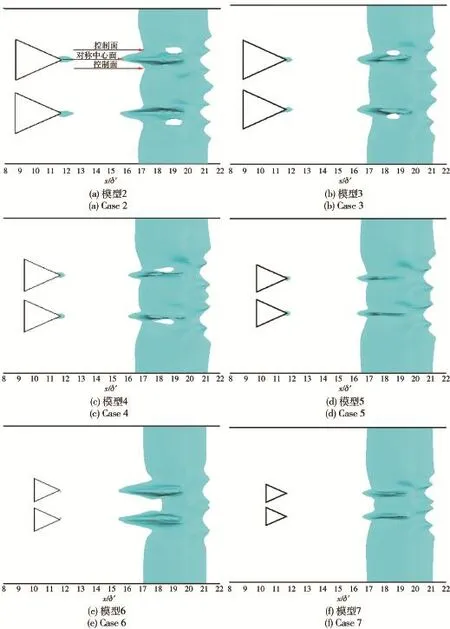
图9 流场流向速度等值面（u=0）Fig.9 Iso-surface of streamwise velocity（u=0）

图11为模型2～模型8流场边界层底层法向截面在控制面上的压力梯度沿x变化曲线。由图11可知，由于激波入射作用，边界层内流体压力梯度在x/δ′=17处（标记①）开始迅速增加，逆压梯度出现，证明此处为边界层初始分离位置，因此逆压梯度的出现与增加是导致边界层分离的重要原因；此后，压力梯度因流经入射激波区域及膨胀波系区域先升高、后降低，故压力在激波入射点上方出现第1峰值（标记②）；压力梯度在x/δ′=19.5处再次出现陡升，在x/δ′=22.5处降至零压力梯度，此时压力出现第2峰值，可确定此处为边界层再附的初始位置（标记③）。图11中模型2～模型7流场两压力梯度峰值明显低于无控流场，减少了逆压梯度对边界层内流体产生的不利影响，其中模型4控制效果最好。

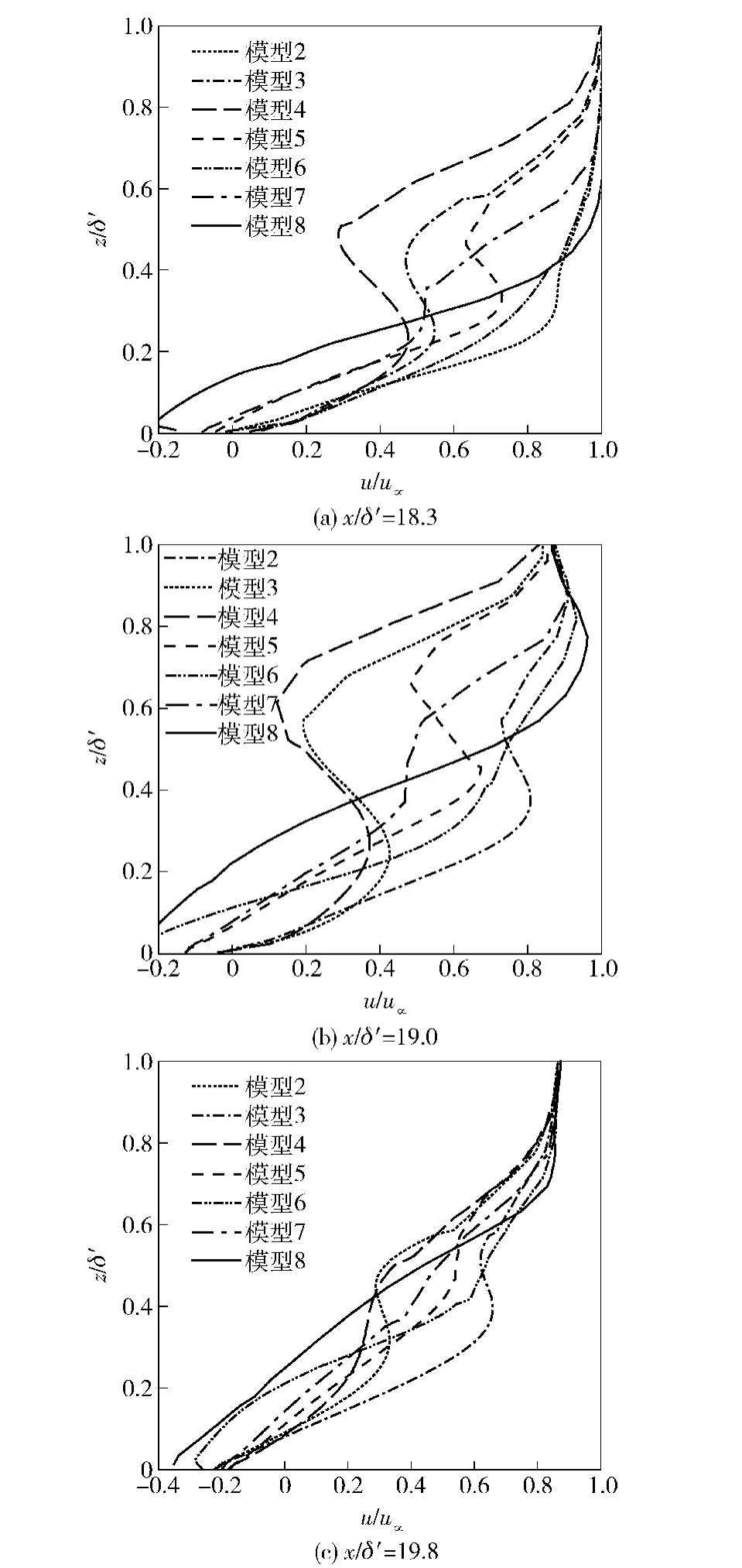
图10 流向涡截面流场流向速度剖面Fig.10 Streamwise velocity profile of boundary layer

图12为模型2～模型8边界层可压形状因子Hr流向分布，图中各点选取控制面上流动分离区域的11个流向位置沿法向积分得到位移厚度δ*及动量厚度θ作比值得出。计算公式如下:

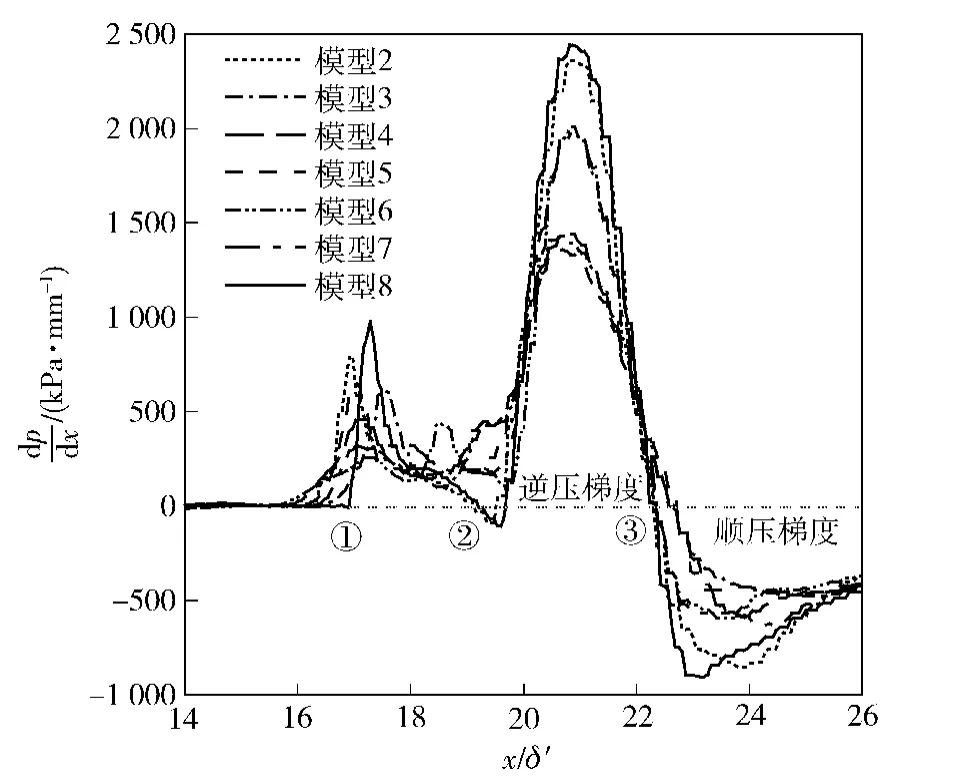
图11　压力梯度沿x变化曲线Fig.11 Distribution of pressure gradient along x

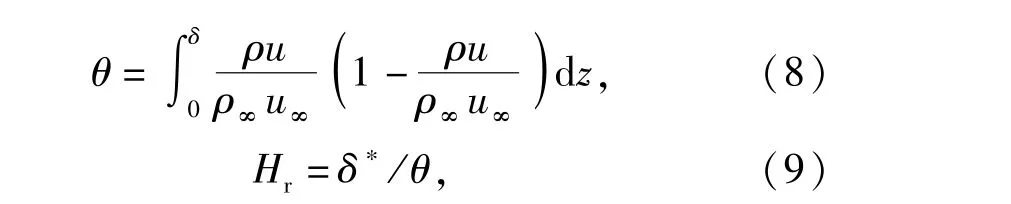
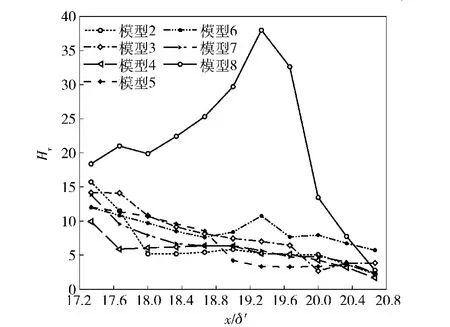
图12　边界层可压形状因子HrFig.12 Transformed form factor of boundary layer

式中:ρ∞为自由来流密度。位移厚度δ*与动量厚度θ分别指由于流体黏性作用，厚度为δ的理想流体流入边界层后所损失的流量与动量。形状因子作为判断微楔控制SWBLI有效性的依据之一，Hr值越大，速度剖面越不饱满，在逆压梯度下越容易出现流动分离，因此，也是评价边界层速度型稳定性的重要指标［24］。由图12可知，模型8边界层形状因子Hr在x/δ′=17.2（流动分离初始位置）约为18.3，此时其上游未受到激波扰动；然而由于流动分离的产生使得边界层Hr值逐渐增大并在x/δ′=19.3处达到峰值，且最大值为37.6.模型2～模型7（有控）相比模型8（无控）分离区域Hr明显减小，原峰值位置Hr值分别减少到15.4、7.0、5.2、3.3、10.7、5.6，且上升趋势沿下游逐渐接近平缓。其中模型4控制效果最理想，峰值降低约86％.

2.3基于不同双微楔高度控制的流场总压损失

总压损失系数Cpt作为整个流场总压损失程度的衡量，可定义为入口总压p0i与出口总压p0o的差值与动压的比值［25］，计算公式如下:

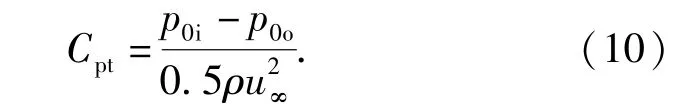
将流动控制用于SWBLI主要有两个目的:抑制激波诱导的流动分离（减小形状因子）和降低总压损失。表2将模型2～模型8流场进出口总压值以及总压损失系数进行对比，分析数据可知:有控流场总压损失均得到减少；对比模型2～模型7控制结果，总压损失系数随着微楔高度的增加呈先减小、后增加的趋势，这是由于微楔几何尺寸越大，所诱导的流向涡越大，涡强度也就越大，对分离区域总压损失的减缓也越明显；然而微楔自身存在附加阻力，尺寸较大的微楔上表面会与边界层内超声速区域相互作用产生形状阻力也就越大，进而增加了部分总压损失。因此，模型4为本文最佳控制配置，且模型4流场比无控流场中的总压损失降低1.9％.

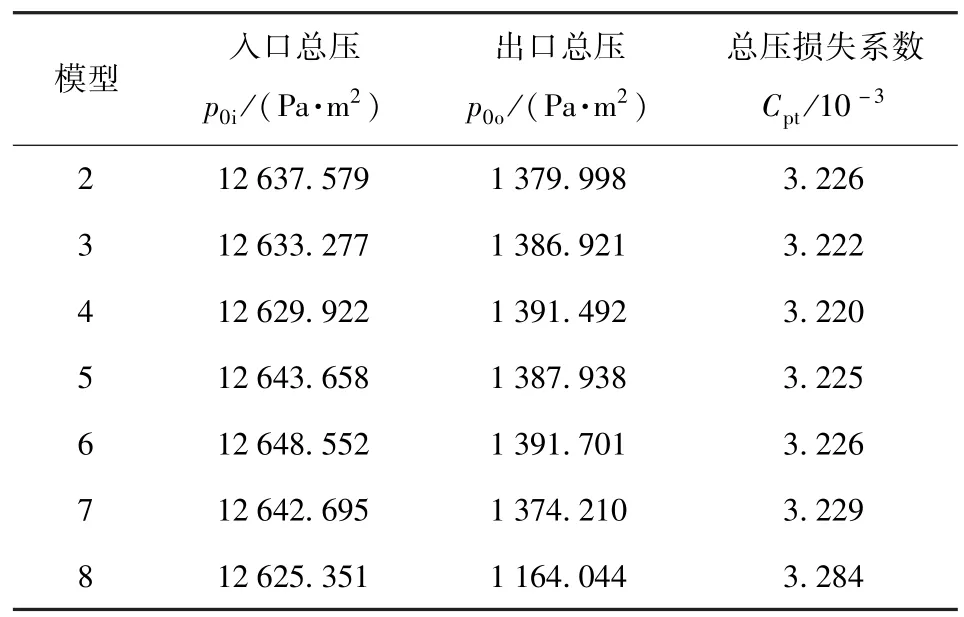
表2　流场控制前后总压损失系数对比Tab.2 Total pressure loss coefficient of flow field before and after control

3　结论

本文对来流马赫数为7.0流场中SWBLI诱导的流动分离及微楔控制过程进行了三维数值模拟，对比分析了单、双微楔的控制机理，并基于边界层流向速度、压力梯度、形状因子及总压损失等参数讨论了微楔高度对SWBLI控制效果的影响，得出主要结论如下:

1）微楔阵列可明显改善高超声速流场中分离边界层，因其诱导的逆旋流向涡对分离边界层内低能流体与外部高能流体起到掺混的作用，使得流场分离区域流向速度剖面更饱满，分离气泡尺寸减小、边界层形状因子减小，边界层稳定性增加。

2）由于双微楔产生的流向涡对与涡对之间的相互诱导促进了各自流向涡对之间的卷吸作用，使得双微楔对分离气泡的消除效果优于单只微楔。

3）由于微楔诱导的流向涡强度与其尺寸呈正比关系，强度大的流向涡可加强边界层内流体与外部高能流体的掺混，增强其抵抗逆压梯度的能力，抑制流动分离减少总压损失，然而微楔自身形状阻力与尺寸同样呈正比关系，这与微楔流向涡强度对控制效果的影响相矛盾。因此，总压损失系数随着微楔高度的增加呈先减小、后增加的趋势。

4）综合讨论形状阻力与流向涡强度对控制效果的影响，高度为35％分离气泡厚度的双微楔控制效果最好:分离区回流厚度局部可减少至回流消失，边界层可压形状因子峰值降低约86％，总压损失降低1.9％.

（References）

［1］ Ferri A，Guidonia A D.Experimental results with airfoils tested in the high speed tunnel at Guidonia，NACA-TM-946［R］.Washington，DC，US:National Advisory Committee for Aeronautics，1940.

［2］ Mallinson SG，Gai SL，Mudford N R.The interaction of a shock wave with a laminar boundary layer at a compressing corner in high-enthalpy flows including real gas effects［J］.Journal of Fluid Mechanics，1997，342:1-35.

［3］ MacComack RW.Numerical solution of the interaction of a shock wave with a laminar boundary layer［J］.Lecture Notes in Physics，1971，8:151-163.

［4］ Urbin G，Knight D D，Zheltovodov A A.Large eddy simulation of a supersonic compression corner.I［C］∥38th Aerospace Sciences Meeting and Exhibit.Reno，NV，US:AIAA，2000.

［5］ Garnier E，Sagaut P，Deville M.Large eddy simulation of shock/ boundary layer interaction［J］.AIAA Journal，2002，40（10）: 1935-1944.

［6］ Knight D，Yan H，Panaras A G，et al.Advances in CFD prediction of shock wave turbulent boundary layer interactions［J］.Progress in Aerospace Sciences，2003，39（2）:121-184.

［7］ Donovan JF.Control of shock wave/turbulent boundary layer interactions using tangential injection［C］∥34th Aerospace Sciences Meeting and Exhibit.Reno，NV，US:AIAA，1996.

［8］ Gefroh D，Loth E，Dutton C，et al.Aeroelastically deflecting flaps for shock/boundary layer interaction control［J］.Journal of Fluids and Structures，2003，17（7）:1001-1016.

［9］ Caraballo E，Webb N，Little J，etal.Supersonic inlet flow control using plasma actuators［C］∥47th Aerospace Sciences Meeting.Orlando，FL，US:AIAA，2009.

［10］ Babinsky H，Ogawa H.SBLI control for wings and inlets［J］. Shock Waves，2008，18（2）:89-96.

［11］ Anderson B H，Tinapple J，Surber L.Optimal control of shock wave turbulent boundary layer interactions using micro-array actuation［C］∥3rd AIAA Flow Control Conference.San Francisco，CA，US:AIAA，2006.

［12］ Lee S，Loth E，Wang C.LES of supersonic turbulent boundary layers with μVG's［C］∥25th AIAA Applied Aerodynamics Conference.Miami，FL，US:AIAA，2007.

［13］ Sharma P，Ghosh S.A novel vortex generator for mitigation of shock-induced separation［C］∥52nd Aerospace Sciences Meeting.National Harbor，MD，US:AIAA，2014.

［14］ Zhang B，Zhao Q，Xiang X，et al.An improved micro-vortex generator in supersonic flows［J］.Aerospace Science and Technology，2015，47:210-215.

［15］ Verma S，Chidambaranathan M.Transition control of Mach to regular reflection induced interaction using an array of micro ramp vane-type vortex generators［J］.Physics of Fluids，2015，27（10）:107102.

［16］ Yan Y，Chen C，Lu P，et al.Study on shock wave-vortex ring interaction by the micro vortex generator controlled ramp flow with turbulent inflow［J］.Aerospace Science and Technology，2013，30（1）:226-231.

［17］ Yan Y，Liu C.Study on the ring-like vortical structure in MVG controlled supersonic ramp flow with different inflow conditions［J］.Aerospace Science and Technology，2014，35（1）:106-115.

［18］ 闫文辉，吴小虹，徐晶磊，等.高马赫数下激波湍流边界层干扰数值研究［J］.航空计算技术，2011，41（5）:56-60. YAN Wen-hui，WU Xiao-hong，XU Jing-lei，et al.Numerical study of shock-wave turbulent boundary layer interaction at high Mach number［J］.Aeronautical Computing Technique，2011，41（5）:56-60.（in Chinese）

［19］ 薛大文，陈志华，孙晓晖，等.微型三角楔超声速绕流特性的研究［J］.工程力学，2013，30（4）:455-460. XUE Da-wen，CHEN Zhi-hua，SUN Xiao-hui，et al.Investigations on the flow characteristics of supersonic flow past a microramp［J］.Engineering Mechanics，2013，30（4）:455-460.（in Chinese）

［20］ 薛大文，陈志华，孙晓晖，等.翼型绕流分离的微楔控制［J］.工程力学，2014，31（8）:217-222. XUEDa-wen，CHEN Zhi-hua，SUN Xiao-hui，etal.Micro-ramp control of the boundary separation induced by the flow past an airfoil［J］.Engineering Mechanics，2014，31（8）:217-222.（in Chinese）

［21］ 刘刚，刘伟，牟斌，等.涡流发生器数值计算方法研究［J］.空气动力学学报，2007，25（2）:241-244. LIU Gang，LIUWei，MU Bin，et al.CFD numerical simulation investigation of vortex generators［J］.Acta Aerodynamica Sinica，2007，25（2）:241-244.（in Chinese）

［22］ Menter F R.Zonal two equation k-ω turbulence models for aerodynamic flow［C］∥24th Fluid Dynamics Conference.Orlando，FL，US:AIAA，1993.

［23］ 刘学强，伍贻兆，程克明，等.用基于M-SST湍流模型的DES方法数值模拟喷流流场［J］.力学学报，2004，36（4）: 401-406. LIU Xue-qiang，WU Yi-zhao，CHENG Ke-ming，et al.Computation of lateral turbulent jets using M-SST DES Model［J］.Acta Mechanica Sinica，2004，36（4）:401-406.（in Chinese）

［24］ Ozawa T，Lesbros S，Hong G.LES of synthetic jets in boundary layer with laminar separation caused by adverse pressure gradient［J］.Computers＆amp;Fluids，2010，39（5）:845-858.

［25］ Canepa E，Lengani D，Satta F，et al.Boundary layer separation control on a flat plate with adverse pressure gradients using vortex generators［C］∥ASME Turbo Expo2006:Power for Land，Sea，and Air.Barcelona，Spain:American Society of Mechanical Engineers，2006:1211-1220.

Research on Control of Hypersonic Shock Wave/boundary Layer Interactions by Double Micro-ramps

DONG Xiang-rui，CHEN Yao-hui，DONG Gang，LIU Yi-xin
（National Key Laboratory of Transient Physics，Nanjing University of Science and Technology，Nanjing 210094，Jiangsu，China）

Shock wave/boundary layer interaction（SWBLI）is a ubiquitous phenomenon encountered in hypersonic flow field，and a flow separation induced by SWBLI leads to the performance degradation of hypersonic inlet.Detached-eddy simulation model and finite volume method are used with adaptive mesh refinement to simulate the flow separation controlled bymicro-ramps，which is induced by SWBLIs in hypersonic flow for Ma=7.The control effect of micro-ramps on flow separation is discussed based on flow velocity，pressure gradient，transformed form factor and total pressure loss，and the control mechanism of double micro-ramps is investigated.The research results indicate that the reciprocal induction between streamwise vortex pairs generated by two micro-ramps accelerates the entrainment of vortex pairs generated by each micro-ramp，consequently the effect of two micro-ramps for eliminating the separation bubble is better than that of a single micro-ramp.As the height of micro-ramps decrease，the total pressure loss shows a trend of first decrease and then increase.The effects of streamwise vortex intensity and form resistance are synthetically discussed.The micro-ramps with 35％δ′in height（separation bubble thickness）have the best effect on controlling the separation bubble，by which the separation bubble is decreased to disappear the reversed flow，and the peak of transformed form factor and the total pressure lossare reduced by about86％and 1.9％，respectively.

fluid mechanics；hypersonic flow；shock wave/boundary layer interaction；micro-ramp；flow separation control；streamwise vortex

O354.4

A

1000-1093（2016）09-1624-09

10.3969/j.issn.1000-1093.2016.09.011

2015-06-11

总装备部预先研究项目（9140C300206150C30143）；江苏省普通高校研究生创新计划项目（KYZZ15_0134）

董祥瑞（1991—），女，博士研究生。E-mail:dongxr1154@126.com；陈耀慧（1979—），男，副研究员，博士后。E-mail:cyh873@163.com