基于3D-SVPWM的三电平电网模拟装置的研究与仿真*

刘　邓，　刘　军，　陶忠正，　李月凡

上海电机学院　上海　201306



基于3D-SVPWM的三电平电网模拟装置的研究与仿真*

刘邓，刘军，陶忠正，李月凡

上海电机学院上海201306

传统三电平空间矢量调制算法计算烦琐，需占用大量资源，大大降低了系统的性能。提出三维空间矢量调制技术对三电平电网模拟装置进行控制，首先针对三电平二极管中点钳位式变流器的三维空间矢量调制算法进行了研究，然后对三维坐标系进行矢量建模计算，最后基于MATLAB进行仿真，从而验证了该方法的可行性。

1　二极管钳位型多电平逆变器简介

目前使用最广泛的是二极管钳位型多电平逆变器，图1为该逆变器的拓扑结构，其特点是采用6个二极管对相应开关元件进行钳位，以保证每个桥臂可以输出正、负、零3种电平。直流分压电容C1=C2，每2个相邻的开关器件同时导通或者关断，(Sj1,Sj3)、(Sj2,Sj4)分别互补[1](j=a、b、c)。

图1　二极管钳位三电平逆变器的拓扑结构

二极管钳位型多电平逆变器的优缺点如下。

优点： ① 电平数越多，输出电压的谐波含量就越小；② 利用电容对直流侧分压，二极管进行中点钳位，可在高压大功率时有效减小装置体积。

缺点： ① 直流侧电容存在分压不平衡问题；② 每个桥臂内外侧功率器件导通时间不均衡，会造成负荷不一致；③ 随着电平数的增多，需要的钳位二极管较多，增加了控制难度，失去了使用价值[2]。

2　三维空间矢量调制算法

2.1三维空间矢量坐标系的建立

由于αβ平面是在三相对称前提下对三维空间的一种描述方法，因此，若将矢量在三维空间中进行描述，可得到如图2所示的三电平变流器的三维空间矢量图。

图2　三维空间矢量图

根据Ua=Ub=Uc=0，3个平面将整个空间分为8个大区(小立方体)，小立方体的数目与变流器的电平数相关。这些小立方体的内部空间构成完全相同，包含的8个矢量只相差一个直流分量，故可通过坐标原点平移的方法将8个小立方体归化到一个立方体中进行分析，这样大大简化了3D-SVM算法[3]。

2.2三维空间矢量调制算法理论分析

三维空间矢量调制算法可分为3步实现： 通过判断三相电压正负及大小，可判断三相电压的合成矢量具体区域；可以确定合成目标所需的矢量；确定具体由哪3个矢量来合成目标后，可以计算出矢量所需的作用时间。

2.2.1三相电压合成矢量所在区域的判断

将计算所得三相参考电压放在Ua、Ub、Uc3个坐标轴上，根据A、B、C三相参考电压的正负可判断出三相电压合成矢量具体位于的区域，判断过程大为简化，避免了烦琐的乘法运算。当a>0、b>0、c>0时，合成矢量位于第一大区，具体的划分结果如图3所示[4]。

图3　大区划分示意图

每个大区可被其所在平面的斜对角面划分为6个四面体小区。这样划分的优点是每个小区都有一个大矢量、一个中矢量和一个小矢量，3个非零矢量。大中小相邻矢量都只有一位不一样，只要控制变流器3个桥臂的组合状态，按照这个顺序变化，可保证每次只有一相的状态发生变化，从而使每次只有一相的开关管切换状态。根据A、B、C三相电压之间的大小关系，能判断出三相电压合成矢量所在的小区。如图4所示，当a>0、b>0、c>0且a>b、b>c时，三相电压合成矢量位于第一大区的第一小区。

图4　第一大区中小区划分示意图

2.2.2三相电压合成矢量作用时间计算

判断出三相电压合成矢量所处的区域后，可以确定具体合成目标矢量的分矢量。假设目标矢量位于图4所在的小区1，那么合成目标矢量所分解成分矢量有(0,0,0)、(0,0,1)、(0,1,1)、(1,1,1)。由伏秒平衡原理可得：

(1)式中：Vref为三相电压合成矢量；Ts为开关周期；V1、V2、V3为合成矢量所在区域非零分矢量；T1、T2、T3为对应分矢量一个开关周期内作用时间。

将式(1)两边同时除以Ts，可得：

(2)

(3)

式中： Vdc为直流母线电压。

(4)

式中： Va、Vb、Vc分别为A、B、C三相相电压。

最终得到：

T1=d1·Ts

(5)

T2=d2·Ts

(6)

T3=d3·Ts

(7)

T0=Ts-T1-T2-T3

(8)

其它区域计算矢量作用时间计算与此类似。

2.2.3三相电压合成矢量作用顺序的确定

三维空间矢量调制要求从一个区域到另一个区域进行切换时要平滑，按照这个原则，基于笔者提出的八象限自然分区法，可以利用零矢量(0,0,0)进行过渡，即每个区域的矢量都以零矢量开始，又以零矢量结束。为了使区域切换时的开关损耗最小，要求每次切换时只能有一相状态变化，同时为了减小电压应力du·dt-1，变化相的状态只能按照类似(0→1→0→-1→0)的状态进行变化。综合上述原则，可以确定一套以零矢量为过渡矢量的七段式矢量作用顺序，如图5所示。下面以区域1为例进行详细分析。

图5　矢量作用顺序

图5中，Ta、Tb、Tc分别为矢量切换时间，根据图5可以推算出其具体表达式：

(9)

(10)

(11)

3　三维空间矢量调制算法仿真分析

为验证之前所述理论的正确性，笔者应用MATLAB R2012b搭建了三电平变流系统摸型，进行了仿真研究。具体仿真参数如下： 三相参考电压Va、Vb、Vc有效值为220V，直流侧母线电压Vdc为800V，开关频率fs为20kHz。搭建的SIMULINK模型如图6所示。

将图7放大后得到图8的放大图，图7为逆变器A相4个开关管的驱动波形，在图8中可以清晰看到，1、3管驱动波形对称互补，2、4管驱动波形对称互补。

图9为直流母线电压，在开始时有很大的超调量，但随后能够稳定在800V左右。图10为逆变器侧三相负载的相电压，可以看到，经过很短时间，输出相电压就能够保持在220V左右。

图11是对图10中的A相电压进行FFT分析。由图11可以知道，逆变器侧A相负载相电压的总谐波畸变率(THD)为1.58%，低于国标(GB/T 14549—1993)规定的5%，说明三维空间矢量调制技术能够有效抑制逆变器由于各种原因引起的波形畸变，达到仿真目的。

4　结论

目前三电平电网模拟装置的控制方法很少，笔者提出的三维空间矢量调制技术是基于SIMULINK的电气仿真，能够对三电平电网模拟装置进行控制，可有效克服传统三电平空间矢量调制算法计算烦琐、占用资源多的缺点，大大提高系统的运算性能。

图6　电网模拟装置仿真模型

图7　A相开关管驱动波形

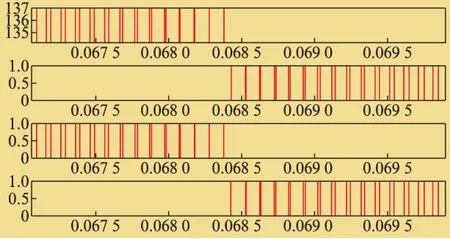
图8　A相开关管驱动波形放大图

图9　整流器侧输出直流电压

图10　逆变器侧ABC三相负载相电压

图11　逆变器侧A相负载相电压FFT分析

[1] 王长兵.三电平逆变器SVPWM控制算法的研究[D].哈尔滨： 哈尔滨工业大学,2002.

[2] 宋文祥,陈国呈,束满堂,等.中点钳位式三电平逆变器空间矢量调制及其中点控制研究[J].中国电机工程学报，2006,26(5)： 105-109.

[3] 吴学智,刘亚东,黄立培.三电平电压型逆变器空间矢量调制算法的研究[J].电工电能新技术，2002,21(4)： 16- 20.

[4] 张德宽.一种实用中点钳位(NPC)逆变器的空间矢量方法[J].电气传动,2003(2)： 4-7,17.

Traditional algorithm with three-level space vector modulation is so tedious that will take up intensive resource while reducing the performance of the system enormously. The proposed approach that adopts three-dimensional space vector modulation technique to control three-level grid simulator has conducted an investigation on modulation algorithm with 3-D space vector for the NPC-type converters with three-level diode in the first step, and then performs vector modeling & computing of 3-D coordinate system. Finally, the feasibility of the method is verified through MATLAB-based simulation.

3-D Space Vector； 3D-SVPWM； Three Electrical Level； Grid Simulator

2015年9月

刘邓(1989—)，男，在读硕士研究生，

E-mail： 1223829846@qq.com

TM464

A

1674-540X(2016)01-033-04

*上海市教委重点学科(编号： J51901)