实时全额支付系统中基于基本环的高效多边撮合算法分析和设计
2016-11-09李世梁
李 世 梁
(中国人民银行上海总部 上海 200120)
实时全额支付系统中基于基本环的高效多边撮合算法分析和设计
李 世 梁
(中国人民银行上海总部上海 200120)
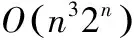
基本环实时全额支付系统清算多边撮合
0 引 言
在跨行转账支付系统中,大额支付系统是各国最重要的支付系统。经大额支付系统处理和清算的支付(资金转账)指令,通常具有数量多、金额大、实时性要求高等特点,已成为连接社会经济活动及其资金运行的“大动脉”。若一家或多家参与机构(成员银行)发生信用或流动性风险,可能会影响整体金融稳定,进而引发系统性金融危机[1,2]。
在跨行转账支付系统中,有两种基本的清算模型:实时全额支付系统(RTGS)和延迟净额结算系统(DNS)。根据国际清算银行的定义,在RTGS中,资金转账指令的处理和最终清算是实时连续的,对参与机构流动性要求高但结算风险小;而在延迟净额结算系统(DNS)中,指令是周期性地在某一时间点进行轧差,能够节约参与者流动性但结算风险较高[1]。为了降低金融风险,RTGS已成为包括中国在内的多数国家构建大额支付系统的主要形式。
由于RTGS的定义非常宽泛,其具体设计实现具有很大的差异性,尤其是当发送参与机构在央行清算账户余额不足时的支付指令处理方式。例如,RTGS可以拒绝这条指令并返回给发送参与机构,或者RTGS可以暂存这条指令(进入排队等待状态),当发送参与机构清算账户余额充足时(解决方法主要是资金注入法,如,央行伦巴第贷款、从其他银行借款、公开市场拆借、等待接收其他参与机构的转账/进账资金),才会释放该条指令。
但使用资金注入法比较困难,会增加参与机构的融资成本,面临央行高额罚息等风险,并且,解决问题的时效性欠佳,可能引起法律风险和声誉受损,例如,某参与机构的客户可能急需转账去完成一笔投资,而资金未实时到账会错过该笔投资。相比较于资金注入法,撮合法在特定条件下可解决“三角债”问题,无需资金注入实现释放(或清算)排队支付指令,可节约参与机构的流动性、提高资金使用效率,已成为支付清算领域中节约参与机构资金流动性的重要手段和研究热点之一[1]。
1 国内外研究现状
为描述方便,本文采用有向图描述法,参与机构代号和其清算账户余额作为节点的属性,其中代号在节点的上部,余额在节点的下部。支付指令抽象为付款方至收款方的有向边,将交易金额作为有向边的权值。
传统撮合法在简化撮合图中利用深度优先搜索法寻找一个可撮合环,可撮合环上的所有节点满足条件:[节点清算账户余额+∑(入边权值)-∑(出边权值)≥0][3,4]。如图1(a)所示,有4条支付指令因支付指令金额大于清算账户余额,导致清算账户余额不足,进入相互循环等待状态(死锁状态)。如图1(b)所示,若参与机构1,2-4同时抵消1元支付交易金额,则各参与机构均满足支付交易金额大于清算账户余额的条件,解除死锁。如图1(c)所示,最后所有支付指令均可得到释放。
通常,简化撮合图往往包括多个可撮合子图,理想状态下,希望一次撮合能找出所有可撮合子图,一次计算完成所有“三角债”的清理[3,4]。
(1) 随机撮合算法(ROA)鉴于时间和成本约束,一般会选择找到一个可撮合环后,就立即进行撮合[3,4]。因此,从全局角度来看,该撮合法是一个典型的贪心算法[5]。
(2) 流动性节约算法(LSM)首先搜索支付指令构成的最小环,即检查是否存在双边撮合支付指令,然后依次检查三边环撮合、四边环撮合……[6]。如果检查到双边/多边环,构成环的支付指令会被撮合。但LSM本质上依然具有贪心算法的特点,没有从全局角度考虑多环之间的关联和优化。
如图1(d)所示,当两个环(<1,2,3,4>与<6,3,5>)共用节点3时,LSM首先会选取<6,3,5>进行检测(ROA有50%的概率会首先选取<6,3,5>进行检测),但节点3显然不满足可撮合条件(1+0-2=-1<0)。因此,LSM会放弃撮合该环。但是,如图1(e)所示,如果能首先考虑<1,2,3,4>,因节点1-4均满足可撮合条件,<1,2,3,4>上的支付指令均可以得到释放,最终,节点3的清算账户余额变为1。然后,再考虑<6,3,5>,发现节点6、3、5均满足可撮合条件。最后,两环均撮合成功。
如图1(f)所示,当两个环(<1,2,3,4>与<6,2,3,5>)共用一条边(<2,3>)时,以上算法均会分别单独考虑两个环。因节点2不满足可撮合条件(1+1-3=-1<0),两环均撮合不成功。然而,如图1(g)所示,如果能同时考虑两个环,则节点2满足可撮合条件(对于节点2而言,1+1+1-3=0),撮合成功。
因此本文研究基于基本环的多边撮合算法,优化撮合性能。
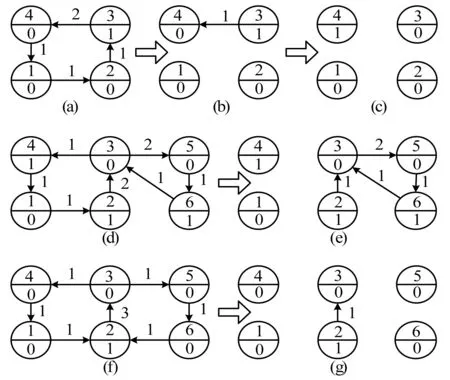
图1 撮合案例
2 问题描述
在RTGS中,各参与机构存储资金或提供质押融资至其央行清算账户,以发送和执行各类贷记指令。参与机构发送的贷记指令,需要同时贷记付款方的清算账户,并借记收款方的清算账户,以维持会计平衡,具有逐笔处理业务、全额清算资金、资金实时到账的特点[1]。
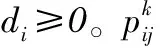
3 基于基本环的多边撮合算法原理和过程
首先对有向图G={V,E}(|V|=n,|E|=m)进行简化处理,进行双边撮合,利用拓扑排序法消除不能构成环的有向边,然后利用查找基本环算法生成全部基本环。对于多环共用公共节点的情况,利用银行家算法得出多环安全推进序列(详见3.4节);对于多环共用有向边的情况,不仅给出多环安全推进序列,还应考虑共同撮合的情景;最后,对支付指令进行消除处理。
3.1有向图简化处理
(1) 双边撮合

复杂度分析:因有向图G中有m条边,则双边撮合的时间复杂度为O(m)。

图2 双边撮合案例
(2) 拓扑排序
有向有环图的一个特点是,所有节点的入度大于0。因此,可得如下定理:
定理1利用拓扑排序可快速消除有向图中不能构成环的节点和边。
证明根据有向无环图的一个定理:如果图G存在一个拓扑排序,则G是一个有向无环图[5]。该定理的逆否命题是:如果图G是一个有向有环图,则G不存在拓扑排序。因此,可利用拓扑排序法,首先在图G中查找一个入度为0的节点v,然后在图G中删除v及其关联的出边,重复此过程,直至图G中不存在入度为0的节点。

图3 拓扑排序案例
如图3(a)所示,首先,节点6的入度为0,则删除节点6及其关联的两条边(p62和p65);然后,如图3(b)所示,节点5的入度由1变为0,同样删除节点5及其关联的一条边(p53);最后,如图3(c)所示,只剩下节点入度大于0的节点(可构成环)。
复杂度分析:设有向图中有n个节点、m条边,则拓扑排序的时间复杂度为O(m+n)[5]。
3.2查找基本环
本文提出的多边撮合算法需要基于有向图的基本环。在查找有向图的所有基本环方面,已经有很多研究。例如,James C.Tiernan提出的查找算法,该算法理解简单、易于使用程序语言实现,其经过路径拓展、环确认、节点关闭、向前推移起始节点等步骤,可获得一个有向图的所有简单基本环[7]。而国内也有针对查找基本环方面的优化算法,例如,王玉英等[8]提出的查找算法,在算法复杂度方面做了一些优化,时间复杂度为O(n32n)。
3.3撮合孤立可撮合环
对于孤立的可撮合环,即环不与其他环相交于任何节点或边(∀i,j∈{1,…,k},V(Ci)∩V(Cj)=∅∧E(Ci)∩E(Cj)=∅),并满足可撮合条件[节点清算账户余额+∑(入边权值)-∑(出边权值)≥0]则立即进行撮合[3,4]。
复杂度分析:因已找到基本环,仅需对环上的节点进行检测和撮合,时间复杂度为O(n)。
3.4公共节点撮合
假设多环C1,C2,…,Ck有一个公共节点(v=V(C1)∩…V(Ck))。如果多环的其他节点(非公共节点)均满足可撮合条件,则利用银行家算法,可避免死锁的产生[9]。

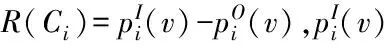
算法1公共节点撮合
初始:v=V(C1)∩…∩V(Ck)
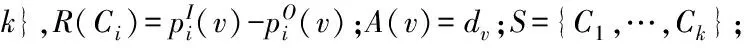
whileS≠φdo
if ∃i,Ci∈S∧R(Ci)+A(v)≥0 then
对环Ci进行撮合;
A(v)=A(v)+R(Ci);
S=S-{Ci};
else
exit();
end
end
复杂度分析:在集合S中查找符合条件的环Ci需要执行k次,集合S的元素数量减少为k-1个,然后继续查找,直至S为空,复杂度为O(k2)。在循环体内,需要执行撮合操作,复杂度为O(n)。因此,算法1的时间复杂度为O(nk2)。


定理2当环C1,C2,…,Ck均无法优先执行撮合时,C1,C2,…,Ck不可共同(同时)撮合。
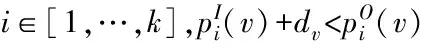
3.5公共边撮合
假设多环C1,C2,…,Ck有一个公共边(e=[v1,v2]=E(C1)∩…E(Ck))。在多环的其他节点(不依附于公共边的节点)均满足可撮合条件的情况下,可按如下步骤进行撮合:(1)利用银行家算法找出安全推进序列;(2)对于无法进行撮合的环,尝试使用公共边共同撮合。
(1) 公共边有序撮合
与算法1类似,利用银行家算法找出公共边安全推进序列。引入变量:环资源需求(R)、公共节点剩余资源量(A),两者均为二维向量。
算法2公共边按序撮合
初始:e=〈v1,v2〉=E(C1)∩…∩E(Ck);A=[dv1dv2]T;

whileS≠∅ do

对环Ci进行撮合;
A=A+R(Ci);
S=S-{Ci};
else
exit();
end
end
复杂度分析:与算法1相同,算法2的复杂度为O(nk2)。但因环资源需求R维度为2(涉及公共边的两个节点),故无法做出排序优化。
(2) 公共边共同撮合
在算法2撮合失败的情况下,若对于该公共边,其起点的入边权值之和加上起点的清算账户余额大于公共边的权值,且其终点的清算账户余额与公共边的权值之和大于终点的出边权值之和(简称“公共边共同撮合条件”),则多环可同时撮合清算。
算法3公共边共同撮合
初始:e=〈v1,v2〉=E(C1)∩…E(Ck);
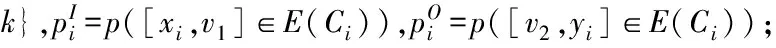

Fori={1..k} do
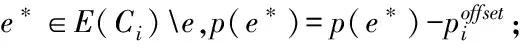
EndFor
Elseexit();
EndIf
复杂度分析:因只需要做一个判定条件,然后对k个环进行撮合,复杂度为O(nk)。
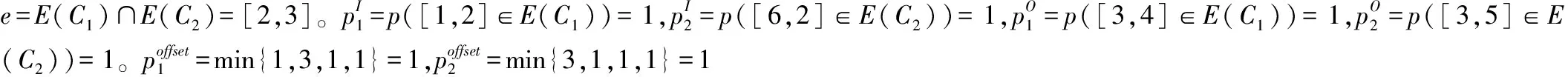

3.6多环有多个公共节点和多个公共边情况分析
(1) 多个公共节点撮合
多环有多个公共节点的情况,可拆分为如下两种情况或两种情况的叠加。
情况1多环依次连续相交于一个公共点。假设多环C1,C2,…,Ck,且∀i∈[1,…,k-1],vi=V(Ci)∩V(Ci+1),则利用算法1,可得到偏序集[A,]。A上的“”关系定义如下:CxCyiff使用算法1,Cy在Cx之前优先执行。然后,通过偏序集构造哈斯图(Hasse)[11],找到偏序集中的极大元y:∀x∈A,x=y(可能不唯一)。最后,使用拓扑排序,得出多环的执行顺序(若哈斯图不是线性图形,则得出的线性序列可能不唯一)。
情况2两环交于多点。假设两环C1、C2交于多点,{v1,v2,…,vm}=V(C1)∩V(C2),则在不同节点分别执行算法1,可得C1、C2的执行顺序∀i∈[1,…,m],C1RiC2。为了综合不同节点处R之间的关系,如表1所示,定义“∘”运算符。若∃i,j∈[1,…,m](i≠j),Ri∘Rj=∅,则两环必须等待,否则按照∀i,j∈[1,…,m],Ri∘Rj顺序执行。

表1 “∘”运算符
(2) 多个公共边撮合
多环有多个公共边的情况,可拆分为如下两种情况或两种情况的叠加。
情况1多环依次连续相交于一条公共边。假设多环C1,C2,…,Ck,且∀i∈[1,…,k-1],ei=〈vi1,vi2〉=E(Ci)∩E(Ci+1),则利用算法2,可得到偏序集[A,]或共同撮合集合S={Ci,C2,…,Cj}⊆{C1,C2,…,Ck}(1≤i≤j≤k),其中S中环的执行顺序依赖于Ci和Cj在偏序集中的执行顺序。若存在偏序集[A,],使得相邻两环CiCi+1,则Ci+1优先执行撮合后,Ci+1上的所有边(支付指令)均得到释放(包括ei=E(Ci)∩E(Ci+1)。因此,缺少了ei这条边,环Ci+1已经被破坏了。为方便生成计算机程序统一处理,可以生成一条ei虚拟支付指令(p(ei)=0)。
情况2两环交于多条边。假设两环C=C1,C2交于多条边,E*={e1,e2,…,em}=E(C1)∩E(C2)。具体执行方法分为如下两种:(1)方法一:类似于3.6.1节情况2的讨论,在不同边分别执行算法2,可得到C1,C2的执行顺序,然后利用“°”运算符得出最终执行顺序;(2)方法二:在方法一失效的情况下,尝试利用算法3,得出可撮合边集合A={e1,e2,…,en}⊆{e1,e2,…,em}(n≤m)。如果E*的所有边均属于可撮合边集合,则环C1,C2可参与公共边共同撮合。
4 方案分析
4.1复杂度分析
本文提出的多边撮合算法经历了双边撮合、拓扑排序、查找基本环、撮合孤立可撮合环、公共节点撮合、公共边撮合等一系列步骤,算法主要的耗费有两点:(1)查找基本环,时间复杂度为:O(n32n);(2)公共节点撮合:O(nklogk)或公共边撮合:O(nk2)。因此,算法总的时间复杂度为:O(max{n32n,nklogk,nk2})=O(n32n)。显然该算法的执行效率主要取决于查找基本环。
4.2算法应用
以下设计较为复杂的案例,然后应用算法解决问题。
(1) 多环交于多点
对与多环交于多点的情况,可拆分为多个两环比较,得出偏序集,然后构造哈斯图,通过拓扑排序得出最终执行顺序。
如图4(a)所示,环C1=<1,2,3,4>与环C2=<3,5,6,7,8,9>交于点3,环C2与环C3=<6,10,8,11,12>交于点{6,8}。首先,在点3处执行算法1,可得C1C2;同样在点6处有C2=C3(R1=″=″),而在点8处有C2≻C3(R2=″≻″)。由于R1∘R2=≻,故C2≻C3。其次,如图5(a)所示,根据环C1、C2与C3之间的偏序关系构造哈斯图,通过拓扑排序得出环执行顺序为C2->C1->C3或C2->C3->C1(图5(b))。如图4(b)所示,因为极大元是C2,优先撮合环C2。最后,C2撮合完成后,环C1和C3显然都变成可撮合环,其执行顺序没有要求。

图4 多环交于多点撮合案例

图5 多环哈斯图
(2) 多环交于多边
对与多环交于多边的情况,可拆分为多个两环比较,得出偏序集或共同撮合集合,然后构造哈斯图,通过拓扑排序得出最终执行顺序。
如图6(a)所示,环C1=<1,2,3,4>与环C2=<2,3,5,6,7,8,9>交于边<2,3>,环C2与环C3=<5,6,12,8,9,10,11>交于边<5,6>和<8,9>。首先,在边<2,3>执行算法2,得到C1≻C2。其次,在边<5,6>上执行算法2,无法得到C2和C3的执行顺序,进而尝试执行算法3,发现C2和C3在边<5,6>上可同时撮合清算。然后在边<8,9>上执行算法3,C2和C3在边<8,9>上亦可同时撮合清算。因为E*上的所有边(<5,6,<8,9>)均属于可撮合边集合,所以C2和C3可参与公共边共同撮合。如图6(b)所示,当环C1优先执行后,边<2,3>被同时释放,环C2事实上已被破坏。为了使得C2和C3可参与同时撮合,生成一条虚拟边<2,3>(p(<2,3>)=0)。最后,环C2和C3参与公共边共同撮合。
显然,算法可以很容易扩展到多环同时交于多点和多边的复杂情况,限于篇幅,本文省略该情景。
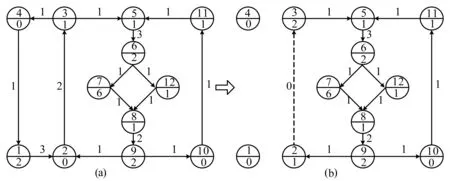
图6 多环交于多边撮合案例
5 结 语
本文算法改进的主要意义是:(1)提出使用双边撮合和拓扑排序对有向图进行简化处理,剩下节点和边必然构成环,通过减少有向图中节点数(n),降低查找基本环算法的时间复杂度过高的影响O(n32n)。(2)从全局角度考虑多环清算,通过考虑公共节点撮合和公共边撮合,提升多边撮合的性能:对于多环共用公共节点的情况,利用银行家算法得出多环的安全推进序列;对于多环共用有向边的情况,不仅给出多环的安全推进序列,还考虑了共同撮合的情景。有效解决了传统撮合法无法进行多环撮合优化的问题,有利于参与机构节约流动性。
对于紧急支付指令,因其时间约束较高,其所在环应优先撮合,但紧急支付指令所在环优先执行撮合后,可能会造成其他环无法撮合,进而影响多边撮合的目标。在应用前景上,本文算法亦可应用于第三方支付、证券交易清算等领域。
[1] Bank for International Settlements.Real-time gross settlement systems[R].Basle.Switzerland,1997.
[2] 陈锡明.支付系统流动性管理研究[J].南方金融,2013(10):85-88.
[3] 田立中,周昭涛,孔昭龙.利用有向图解决支付清算中的“三角债”问题[J].今日科苑,2007,11(20):112.
[4] 孔昭龙.利用有向图解决支付清算中的“三角债”的改进[J].今日科苑,2010,14(8):365.
[5] Jon Kleinberg,Eva Tardos.Algorithm design-影印版[M].北京:清华大学出版社,2012.
[6] Xiaonan Che.Markov type models for large-valued interbank payment systems[D].London School of Economics & Political Science,2011.
[7] James C Tiernan.An efficient search algorithm to find the elementary circuits of a graph[J].Communications of the ACM,1970,13(12):273-276.
[8] 王玉英,陈平,苏旸.生成有向图中全部简单回路的一种有效算法[J].计算机应用与软件,2009,26(12):27-29,33.
[9] Silberschatz A,Galvin P B,Gagne G.Operating System Concepts[M].9th ed.Wiley publication,2012.
[10] Main M,Savitch W.Data Structures and other Objects Using C++(Fourth Edition)影印版[M].北京:科学出版社,2012.
[11] H R Kenneth.Discrete Mathematics and its Application[M].北京:机械工业出版社,2012.
ANALYSIS AND DESIGN OF ELEMENTARY CIRCLES-BASED EFFICIENT MULTILATERAL OFFSETTING ALGORITHM IN REAL TIME GROSS SETTLEMENT SYSTEM
Li Shiliang
(The People’s Bank of China Shanghai Head Office,Shanghai 200120,China)
Traditional offsetting methods will immediately start to offset after finding an executable offsetting circle,which belong to the typical greedy algorithm.In view of this,the paper proposes an algorithm from the global perspective to consider the multi-cyclic clearing.First,the algorithm adopts bilateral offsetting and topological ordering to simplify a directed graph,and the rest of nodes and edges must constitute circles,which improves the efficiency of basic circles searching algorithm (time complexity:O(n32n)).In the case of multi-cyclic sharing common vertexes,the algorithm utilises the bank’s algorithm to obtain an orderly offsetting sequence.In the case of multi-cyclic sharing directed edges,the algorithm not only provides a multi-cyclic orderly offsetting sequence,but also considers the circumstance of common offsets.Through the above steps,the performance of the multilateral offsetting is improved,which saves the liquidity of participants and improves the efficiency of fund utilisation.Finally,the time complexity of the algorithm is analysed,and complex case applications (e.g.multi-cyclic sharing common multi-vertexes or multi-edges) are presented.
Elementary circlesReal time gross settlement systemClearingMultilateral offsetting
2015-05-29。李世梁,工程师,主研领域:支付清算系统,计算机网络。
TP3
A
10.3969/j.issn.1000-386x.2016.09.069
