均匀带电圆盘电场的数值研究

沈华嘉

(广东第二师范学院 物理与信息工程系， 广东 广州 510303)



均匀带电圆盘电场的数值研究

沈华嘉

(广东第二师范学院 物理与信息工程系， 广东 广州 510303)

用通用软件Mathematica对均匀带电圆盘电场的空间分布进行数值研究，对比了勒让德级数解与叠加原理-直接积分两种方法的数字化结果. 结果显示：由勒让德级数解很难绘制出正确的电场强度的空间分布图，而使用积分表达式则可快速获得正确的结果.

均匀带电圆盘；电场；数字化；勒让德级数；积分表达式

1　均匀带电圆盘电势和电场强度的勒让德级数表达式和积分表达式

根据文献[2]，均匀带电圆盘的电势可表达为以勒让德多项式为基的级数

(1)

式中q为圆盘的带电量，a为圆盘的半径，θ为球坐标系的极角．

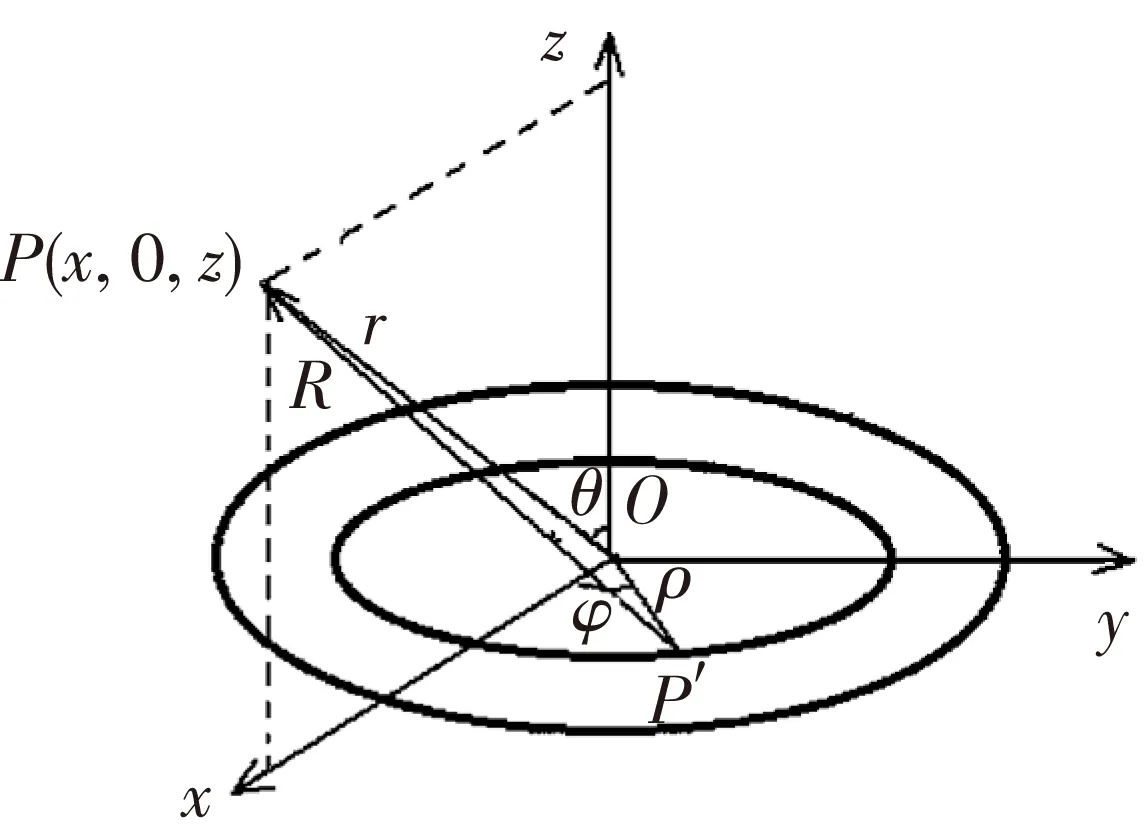
图1　薄圆盘与坐标系

实际上，本问题的电势可以使用叠加原理-积分法来计算. 薄圆盘可以看成由无穷多个同心圆环组成，如图1所示.

由于具有轴对称性，只需考虑xoz平面内观测点P(x,0,z)的电势和电场强度．圆盘上源点P′的坐标为(ρcos φ,ρsin φ,0)，观测点P到源点P′的距离为

(2)

把式(2)代入点电荷的电势公式，由叠加原理得均匀带电圆盘的电势积分表达式

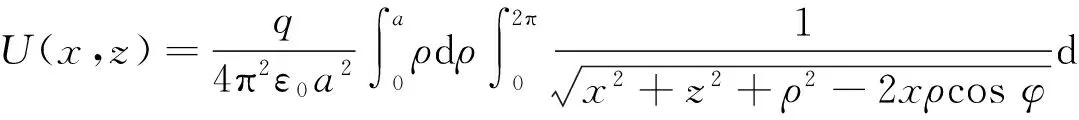
(3)

2　两种表达式的数字化

先给出电势积分表达式的数字化.

设圆盘带正电，为了计算的方便，取长度单位为a，电势单位为U0=q/(4π2ε0a), 电场强度单位为E0=q/(4π2ε0a2). 式(3)是一个复杂的积分, 不能用初等函数表示，可进行数值积分. 为了方便，记

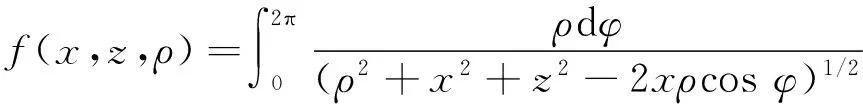
(4)

则电势和电场强度分别为

(5)

和

(6)

根据式(4)～式(6)，由通用软件Mathematica可快速得到电势和电场强度数字化结果，图2～图4分别是电势的空间分布、电场强度大小的空间分布、等势线和电场强度方向的分布，它们形象美观地描述了均匀带电圆盘电场的空间分布.

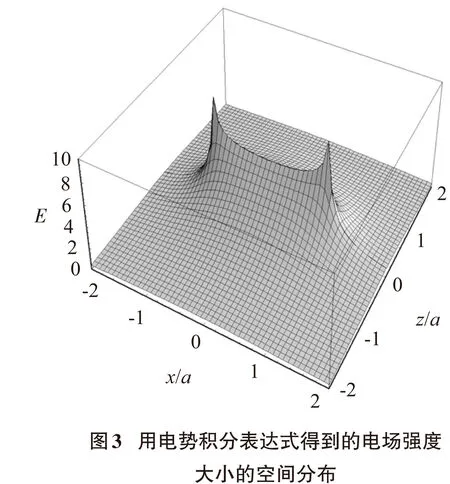
现在开始研究勒让德级数解的数字化.

式(1)是两个以勒让德多项式为基的级数，数值计算的首要问题就是如何快速给出任意阶勒让德多项式. 幸运的是，在Mathematica里勒让德多项式的产生并非难事，无论是直接调用系统内设函数Legendre[2n,x], 还是使用著名的罗德里格斯(Rodrigues)公式

(7)

都可以快速获得2n阶勒让德多项式，例如0、2、4、6阶勒让德多项式分别如下

它们看上去整齐简单，然而，随着阶数的增加，它变得越来越复杂. 当阶数高到一定程度(例如100阶)时，它的复杂程度将超出了我们的想象.

为了获得xoz平面内直观分布图，必须把极坐标系转换成直角坐标系

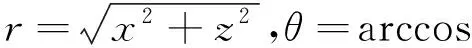
(8)

将式(7)和式(8)代入式(1)，利用Mathematica快速产生勒让德多项式、求和运算以及数字绘图功能，可把式(1)所示的电势表达式数字化. 我们无法求出级数U1和U2的所有项，可以先取级数前21项(截断到n=M=20)，即计算到40阶勒让德多项式，此时由级数表达式(1)得到的电势空间分布与使用电势积分表达式(3)所得到的结果(图2)是一致的.

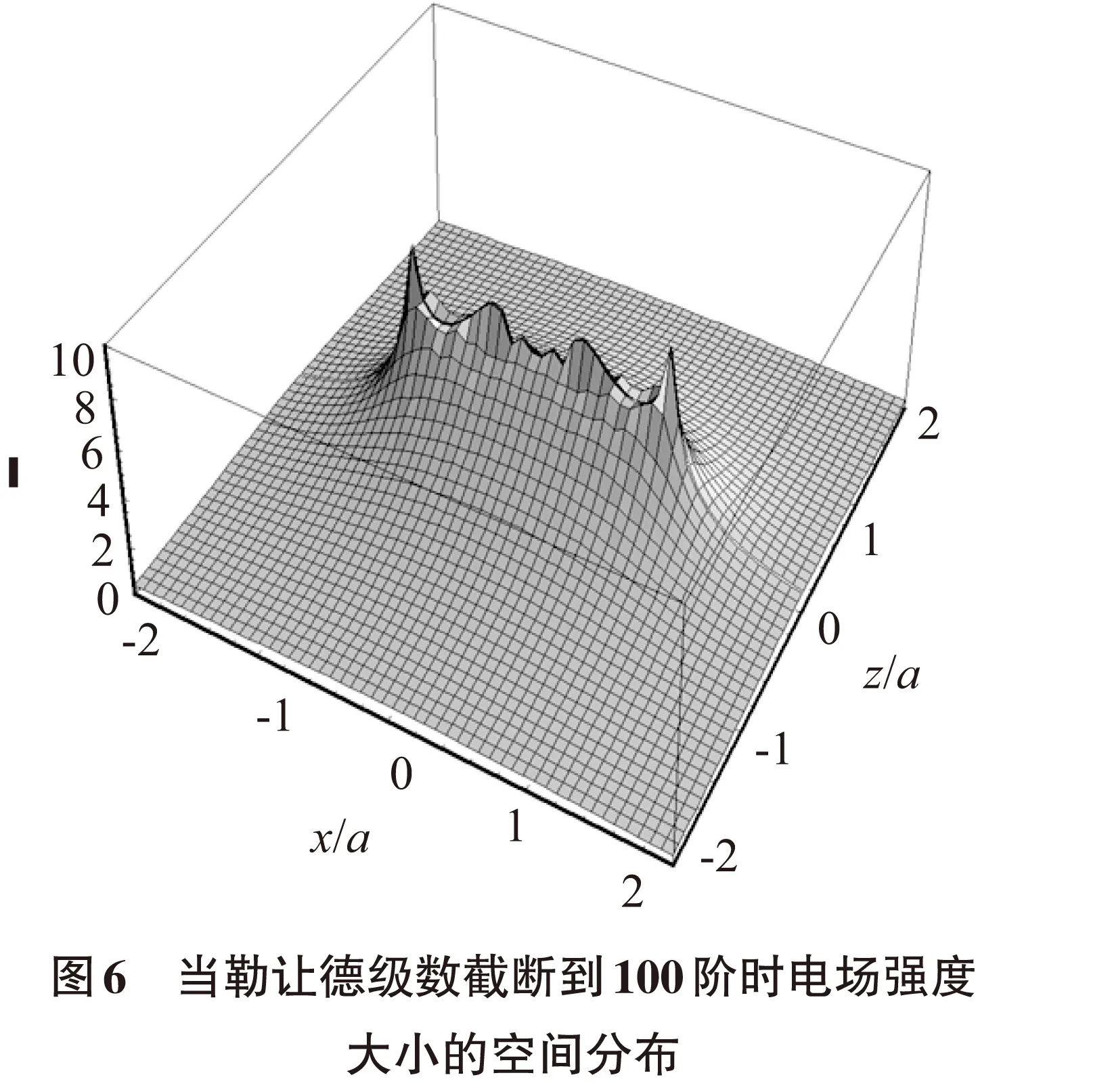
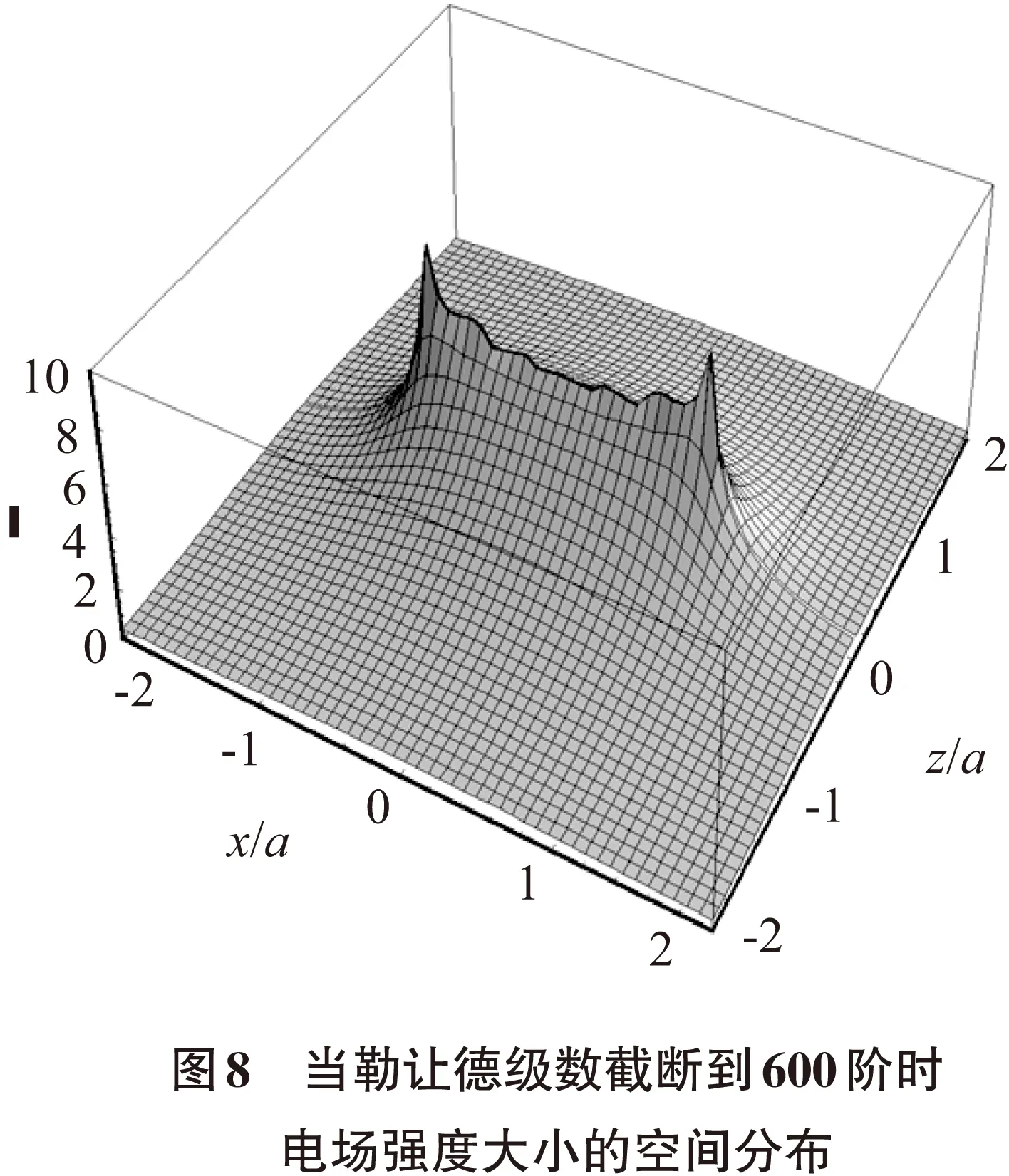
从理论上讲，使用式(6)计算电势的梯度就可得到电场强度. 然而, 当截断到40阶勒让德多项式时，在r

提高计算量至100阶勒让德多项式，结果如图6所示，电场强度大小的分布图有所改善(斑块减少)，但不十分明显；继续提高计算量，当截断到200阶勒让德多项式，数值结果如图7所示，电场强度大小的分布图有了较大改善，但是在圆盘面附近，波动起伏仍十分明显；继续提高截断阶数，结果进一步改善，勒让德级数的结果更进一步接近积分表达式的结果(图3)，当计算到600阶时结果如图8所示，整体已经比较接近图3，但在圆盘面附近仍有比较明显的波动起伏.

3　结论与讨论

本文应用通用软件Mathematica，对均匀带电圆盘电势和电场强度的勒让德级数解进行数字化研究，并与叠加原理-积分法(积分表达式)的结果进行了比较. 结果表明：使用积分表达式可以快速把电势和电场强度数字化(计算并绘制出图2～图4三幅精美分布图只需几秒钟时间). 但使用勒让德级数解则很难把电场强度数字化，现总结如下，以便对勒让德级数有更清晰的认识.

1)对于电势空间分布，使用勒让德级数解，比较容易获得正确的数字化结果，只需截断到第40阶勒让德多项式就可获得正确结果.

2) 对于电场强度的空间分布，使用勒让德级数解，很难获得正确的数字化结果. 就均匀带电圆盘的电场强度而言，在r

[1] 吴崇试．均匀带电薄圆盘的电势问题[J]．大学物理, 2000, 19(11)：1-4.

[2] 林璇英，张之翔．电动力学题解[M]. 2版．北京：科学出版社，2007:152-157.

[3] 贾秀敏．均匀带电圆环片的空间静电场[J]．大学物理, 2010, 29(8)：29-30.

Numerical Study of Electric Field from a Uniform Charged Disc

SHEN Hua-jia

(Department of Physics and Information Engineering, Guangdong University of Education, Guangzhou, Guangdong, 510303, P.R.China)

The spatial distribution of the electric field from a uniform charged disc is numerically studied. The numerical results of Legendre series are compared with ones of the direct integral method. Our results show that it is difficult to draw the correct spatial distribution map of the electric field intensity by using the Legendre series, while using the integral expression the correct results can be quickly obtained.

uniform charged disc; electric field; digitization; Legendre series; integral expression

2016-06-25

广东省高等学校物理专业综合改革试点项目(9010-14246)

沈华嘉，女，浙江绍兴人，广东第二师范学院物理与信息工程系副教授.

O441.3

A

2095-3798(2016)05-0067-04