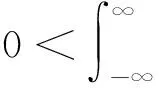
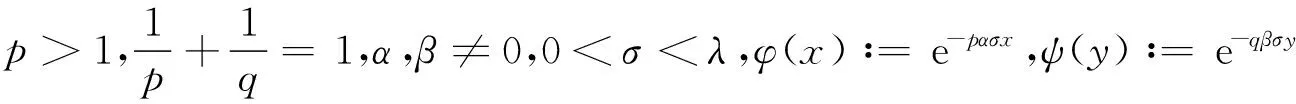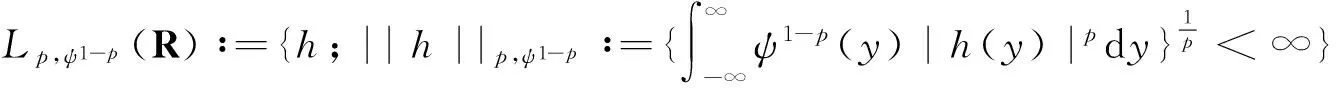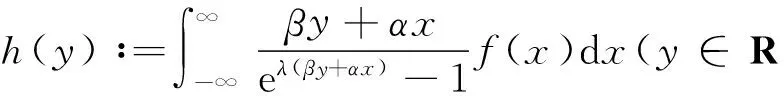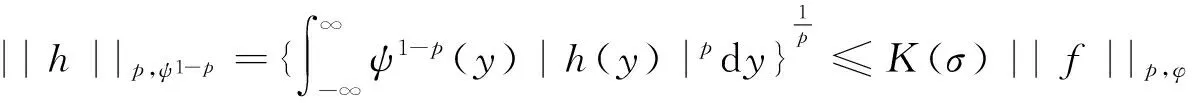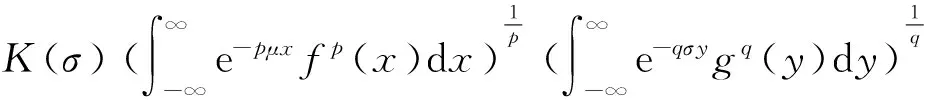一个联系指数函数的全平面Hilbert积分不等式
2016-11-09黄启亮杨必成
黄启亮, 杨必成
(广东第二师范学院 数学系, 广东 广州 510303)
一个联系指数函数的全平面Hilbert积分不等式
黄启亮, 杨必成
(广东第二师范学院 数学系, 广东 广州 510303)
引入独立参量与指数函数中间变量,应用权函数的方法及实分析技巧,建立一个具有最佳常数因子的全平面Hilbert型积分不等式.考虑了其等价式、逆式及特殊参数的齐次与非齐次不等式;还求出了等价不等式的算子及范数表示.
权函数;全平面Hilbert型积分不等式;等价式;全平面Hilbert型积分算子;范数
0 引言
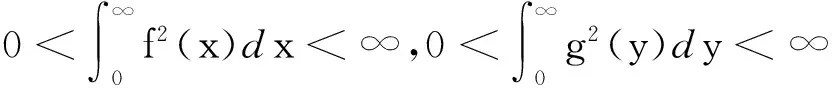
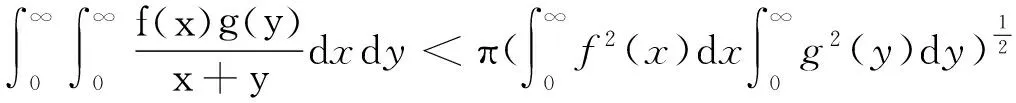
(1)
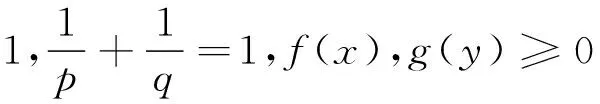

(2)

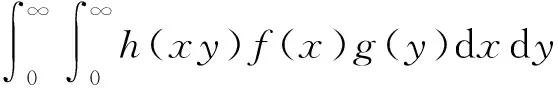
(3)
1998年,文[5-6]中引入独立参量λ∈(0,∞)及beta函数,推广式(1)为
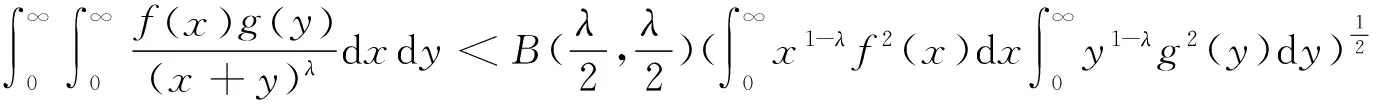
(4)
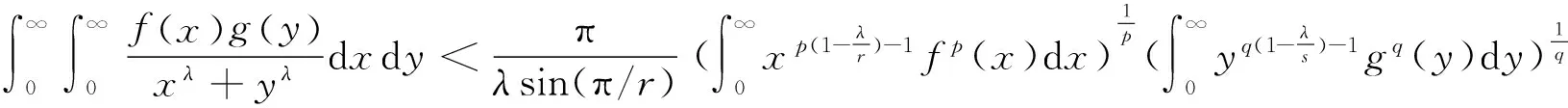
(5)
(6)
2009年,文[22]综述了参量化负数齐次核Hilbert型不等式的一系列研究思想. 2013年,文[23]论述了齐次与非齐次核Hilbert型积分不等式的等价联系.
2007年,文[24]发表了如下具有最佳常数因子的全平面非齐次核Hilbert型积分不等式:
(7)
随后,文[25-32]继续讨论了这一课题. 2009-2014年,杨在专著[21,33-37]中详细论述了一般实数齐次核参量化Hilbert型不等式及其算子刻画的理论.该理论凸显了引入独立参数及两对共轭指数的参量化思想,且讨论了Hilbert型积分算子的范数合成性质,它改进及推广了文[3]的理论成果;文[38]则全面综述了近代Hilbert型不等式理论的研究思想及方法.
本文引入独立参量及指数函数中间变量,应用权函数的方法及实分析技巧,建立如下一个类似于式(7)的具有最佳常数因子的全平面齐次核Hilbert型积分不等式:
(8)
(λ>0).考虑了其引入独立参量的更一般形式、等价式、逆式及特殊参量的齐次及非齐次形式;定义了全平面Hilbert型积分算子,并求出了等价不等式的算子及范数表示.
1 权函数与初始积分不等式
定义1设α,β≠0,0<σ<λ.定义如下权函数:
(9)
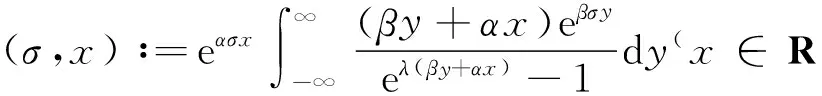
(10)
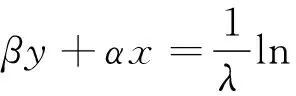
(11)
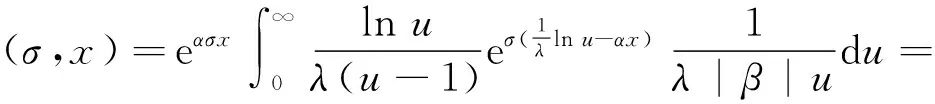
(12)
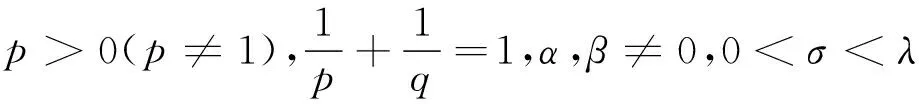
(13)
(14)
(ii) 若0 证明 (i) 当p>1时,配方并由带权的Hölder不等式[39]及式(9),有 (15) 由式(11)及交换积分次序的Fubini定理[40],有 (16) 再由式(12)及式(13),有式(14). (ii) 当0 (17) (18) (19) 证明配方,并由Hölder不等式,有 (20) 故得式(14),且它与式(17)等价. 任给足够大的n∈N (N为正整数集),定义集合Eα∶={x∈R;αx≥0},Fβ∶={y∈R;βy≤0},及 则可算得 对上式作变换 u=eλ(βy+αx),应用交换积分次序的Fubini定理,我们有 由上面计算结果,有 (21) (22) 及化简得K(σ)≤k.故k=K(σ)为式(17)的最佳值. 式(14)的常数因子K(σ)必为最佳值,不然,由式(20),必导出式(17)的常数因子也不为最佳值的矛盾.证毕. 定理3在定理2的条件下,若把p>1改成0 故得式(14)的逆式,且它与式(17)的逆式等价. 若有常数k≥K(σ),使取代式(17)的逆式的常数因子K(σ)后仍成立,任给足够大的n∈N,则可得式(21)的逆式. 而 令n→∞,式(21)的逆式可化为式(22)的逆式,即有K(σ)≥k.故k=K(σ)为式(17)的逆式的最佳值.式(14)的逆式的常数因子必为最佳值,不然,由式(20)的逆式必导出式(17)的逆式的常数因子也不为最佳值矛盾.证毕. 由式(14),有 (23) 定义2定义全平面Hilbert型积分算子T:Lp,φ(R)→Lp,ψ1-p(R)为:任f∈Lp,φ(R),唯一确定Tf=h∈Lp,ψ1-p(R).称式(23)为算子T所对应的不等式. 由定理2,式(23)的常数因子是最佳的,故得 (24) 则式(17),式(14)可改写成如下等价的算子与范数表示式: (Tf,g)<||T||·||f||p,φ||g||q,ψ,||Tf||p,ψ1-p<||T||·||f||p,φ. (25) 评注在式(17)与式(14)中,令α=-1,β=1,μ=λ-σ(>0),以eλxf(x)取代f(x),则有 (26) (27) [1] SCHUR I. Bernerkungen sur Theorie der beschrankten Billnearformen mit unendlich vielen Veranderlichen[J]. J Math,1911,140:1-28. [2] HARDY G H. Note on a theorem of Hilbert concerning series of positive terms[J]. Proceedings London Math Soc,1925,23(2):Records of Proc xlv-xlvi. [3] HARDY G H,LITTLEWOOD J E,POLYA G. Inequalities[M]. Cambridge:Cambridge Univ Press,1952. [4] MITRINOVIC D S,PECARIC J E,FINK A M. Inequalities involving functions and their integrals and derivatives[M]. Boston:Kluwer Academic Publishers,1991. [5]YANG Bi-cheng. On Hilbert′s integral inequality[J]. Journal of Mathematical Analysis and Applications,1998,220:778-785. [6] YANG Bi-cheng. A note on Hilbert′s integral inequality[J]. Chinese Quarterly,1998,13(4):83-86. [7] YANG Bi-cheng,RASSIAS Th M. On the way of weight coefficient and research for Hilbert-type inequalities[J],Math Ineq Appl,2003,6(4):625-658. [8] YANG Bi-cheng. On an extension of Hilbert′s integral inequality with some parameters[J]. The Australian Journal of Mathematical Analysis and Applications,2004,1(1):1-8. [9] YANG Bi-cheng. On the norm of an integral operator and application[J]. Journal of Mathematical Analysis and Applications,2006,321:182-192. [10]YANGBi-cheng.OnthenormofaHilbert’stypelinearoperatorandapplications[J].JMathAnalAppl,2007,325:529-541. [11]YANGBi-cheng,BRNETICI,KRNICM,etal.GeneralizationofHilbertandHardy-Hilbertintegralinequalities[J].MathIneqandAppl,2005,8(2):259-272. [12]KRNICM,PECARICJE.Hilbert′sinequalitiesandtheirreverses[J].PublMathDebrecen,2005,67(3-4):315-331. [13]HONGYong.OnHardy-Hilbertintegralinequalitieswithsomeparameters[J].JIneqinPure&AppliedMath,2005,6(4):1-10. [14]BRNETICI,PECARICJE,GeneralizationsofHilbert′sintegralinequality[J].MathIneq&Appl,2004,7(2):199-205. [15]KRNICM,PECARICJE.GeneralHilbert′sandHardy′sinequalities[J].MathIneq&Appl,2005,8(1):29-51. [16]ARPADB,CHOONGHONGO.Bestconstantforcertainmultilinearintegraloperator[J].JournalofInequalitiesandApplications,2006,no.28582. [17]KUANGJi-chang,DEBNATHL.OnHilbert′stypeinequalitiesontheweightedOrliczspaces[J].PacificJApplMath,2007,1(1):95-103. [18]LIYong-jin,HEBing.OninequalitiesofHilbert′stype[J].BulletinoftheAustralianMathematicalSociety,2007,76(1):1-13. [19]ZHONGWu-yi,YANGBi-cheng.OnmultipleHardy-Hilbert′sintegralinequalitywithkernel[J].JournalofInequalitiesandApplications,2007,ArtID27962,17pages,doi:10.1155/ 2007/27. [20] 杨必成. 一个Hilbert型积分不等式[J].浙江大学学报(理学版),2007,34(2):121-124. [21] 杨必成.算子范数与Hilbert型不等式[M].北京:科学出版社,2009. [22] 杨必成.参量化的Hilbert型不等式研究综述[J].数学进展,2009,38(3):257-268. [23] 杨必成.论Hilbert型积分不等式及其算子表示[J].广东第二师范学院学报,2013,33(5):1-17. [24]YANGBi-cheng.AnewHilbert’stypeintegralinequality[J].SoochowJournalofMathematics,2007,33(4):849-859. [25] 杨必成. 一个新的参量化Hilbert型积分不等式[J].吉林大学学报(理学版),2008,46(6):1085- 1090. [26]XINDong-mei,YANGBi-cheng.AHilbert-typeintegralinequalityinthewholeplanewiththehomogeneouskernelofdegree-2[J].JournalofInequalitiesandApplications,2011,ArticleID401428,11pages,doi:10.1155/2011/401428. [27]WANGAi-zhen,YANGBi-cheng.AnewHilbert-typeintegralinequalityinthewholeplanewiththenon-homogeneouskernel[J].JournalofInequalitiesandApplications,2011:123,doi:10.1186/1029-242X-2011-123. [28]XIEZi-tian,RAJARAMAGANDHIK,ZENGZheng.AnewHilbert-typeintegralinequalitywiththehomogeneouskernelofrealdegreeformandtheintegralinwholeplane[J].BulletinofSocietyforMathematicalServices&Applications,2013,2(1):95-109. [29]XIEZi-tian,ZENGZheng.AnewHilbert-typeinequalityinwholeplanewiththehomogeneouskernelofdegree0[J].i-manager′sJournalonMathematics,2013,2(1):13-19. [30]XIEZi-tian,ZENGZheng,SUNYu-feng.AnewHilbert-typeinequalitywiththehomogeneouskernelofdegree-2[J].AdvancesandApplicationsinMathematicalSciences,2013,12(7):391-401. [31]YANGBi-cheng,CHENQiang.TwokindsofHilbert-typeintegralinequalitiesinthewholeplane[J].JournalofInequalitiesandApplications,2015:21. [32]RASSIASMTh,YANGBi-cheng.AHilbert-typeintegralinequalityinthewholeplanerelatedtothehypergeometricfunctionandthebetafunction[M].JournalofMathematicalAnalysisandApplications,2015,428(2):1286-1308. [33]YANGBi-cheng.Hilbert-typeintegralinequalities[M].TheUnitedArabEmirates:BenthamSciencePublishersLtd,2009. [34]YANGBi-cheng.DiscreteHilbert-typeinequalities[M].TheUnitedArabEmirates:BenthamSciencePublishersLtd,2011. [35]YANGBi-cheng.TwokindsofmultipleHalf-discreteHilbert-typeinequalities[M].Berlin:LambertAcademicPublishing,2012. [36]YANGBi-cheng.TopicsonHalf-discreteHilbert-typeInequalities[M].Berlin:LambertAcademicPublishing,2013. [37]YANGBi-cheng,DEBNATHL.Half-discreteHilbert-typeInequalities[M].Singapore:WorldScientificPublishingCoPteLtd,2014. [38]DEBNATHL,YANGBi-cheng.RecentdevelopmentsofHilbert-typediscreteandintegralinequalitieswithapplications[J].InternationalJournalofMathematicsandMathematicalSciences,2012,ArticleID871845,29pages. [39] 匡继昌.常用不等式[M].济南:山东科技出版社,2004. [40] 匡继昌.实分析与泛函分析(续论)(上册)[M].北京:高等教育出版社,2015. A Hilbert-Type Integral Inequality in the Whole Plane Related to the Exponential Function HUANG Qi-liang, YANG Bi-cheng (Department of Mathematics, Guangdong University of Education, Guangzhou,Guangdong, 510303, P. R. China) By introducing independent parameters and interval variables, applying the weight functions and using technique of real analysis, a Hilbert-type integral inequality in the whole plane related to the exponential function with a best possible constant factor is provided. The equivalent forms, the reverses, the related homogeneous homes and non-homogeneous forms with particular parameters are considered. The operator expressions with the norm for the equivalent inequalities are obtained. weight function; Hilbert-type integral inequality in the whole plane; equivalent form; Hilbert-type integral operator in the whole plane; norm 2016-06-26 国家自然科学基金资助项目(61370186); 广东第二师范学院教授博士科研专项基金资助项目(2015ARF25) 黄启亮,男,广西桂林人,广东第二师范学院数学系教授. O178 A 2095-3798(2016)05-0021-08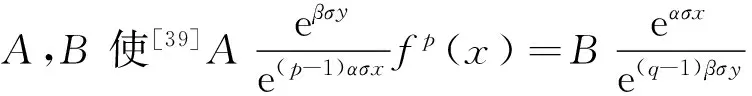
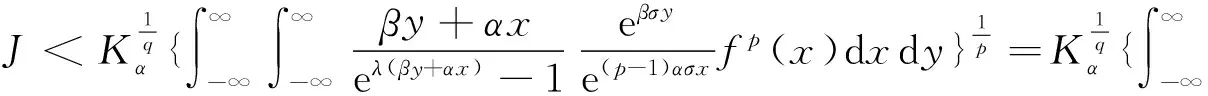
2 具有最佳常数因子的等价不等式及逆式
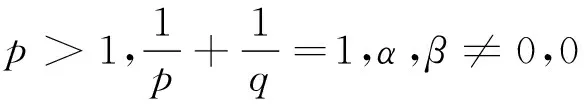


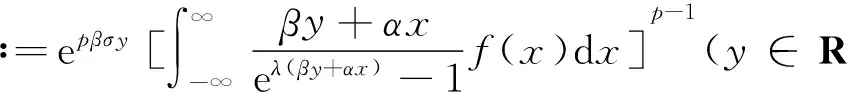
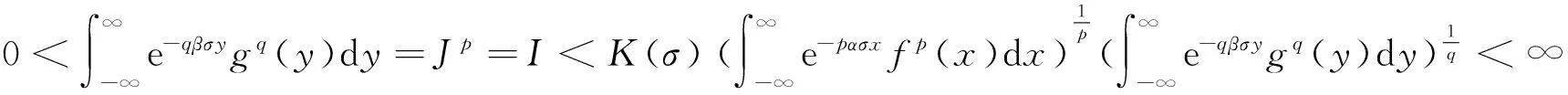
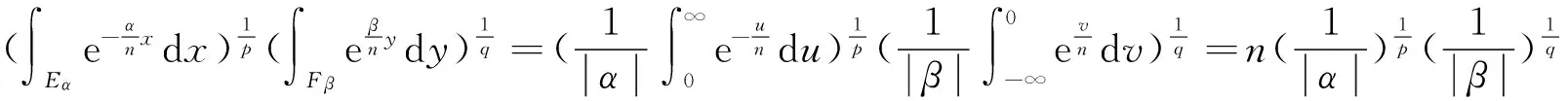
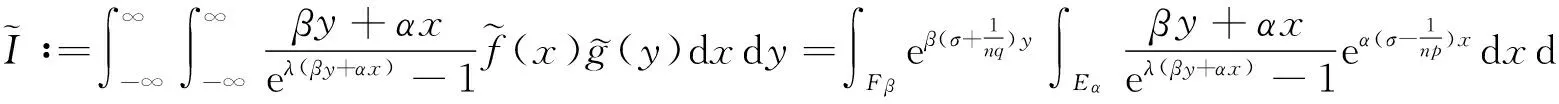
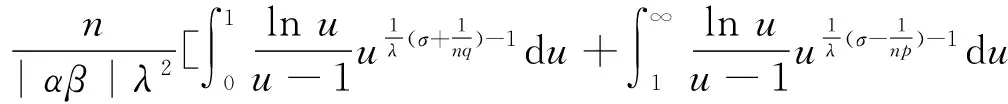


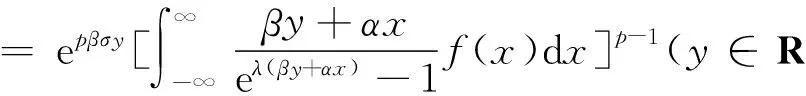
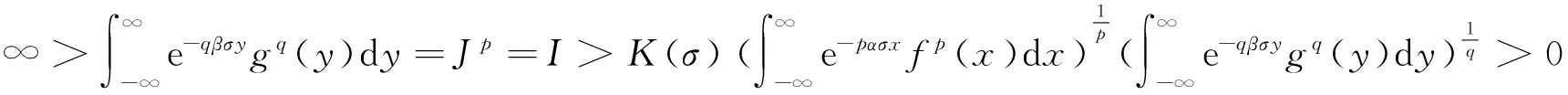
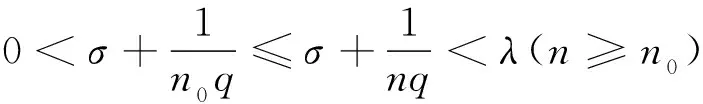

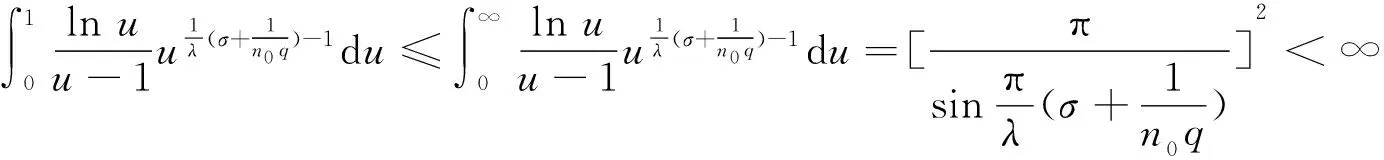
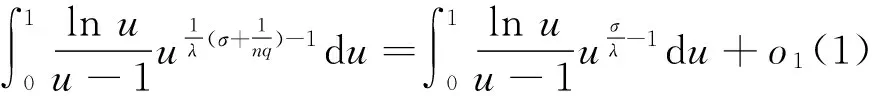
3 等价不等式的算子刻画