再谈三角形几何不等式的s,R,r分拆证明

刘保乾

(西藏自治区组织编制信息管理中心， 西藏 拉萨 850000)



再谈三角形几何不等式的s,R,r分拆证明

刘保乾

(西藏自治区组织编制信息管理中心， 西藏 拉萨 850000)

对三角形几何不等式的s,R,r分拆证明进行了探讨，讨论了分拆算法和程序；大量的例子表明，文中的分拆算法虽然只是试探性的，但可以方便地解决一些难度较大的问题；通过带约束条件的非负分拆，解决了一类根式型不等式问题；给出了杨学枝不等式、walker不等式的新证明；提出并初步讨论了角代换可扩展不等式.

三角形几何不等式；非负分拆；角代换可扩展不等式；机器证明

关于三角形几何不等式的s,R,r分拆证明，文献[1-2]笔者曾探讨过.由于三角形几何不等式一直是初等数学研究的热点，许多三角形几何不等式可化为关于s,R,r的不等式，故这类不等式的证明十分关键.本文拟对s,R,r不等式的非负分拆进行专门研究，以期进一步完善不等式自动发现与判定程序agl2012[3]的功能，更好地解决实际问题.

据本文作者考证，关于s,R,r不等式的非负分拆证明最初源于江苏褚小光的一些论文，时间大约在1999年前后，文献[2]对此背景进行过交待.也正是因为禇先生曾手工分拆证明过一些难度甚大且形式较复杂的不等式问题，人们才对他高超的运算技巧和运算能力印象深刻，s,R,r分拆证明也开始逐渐被人们所重视和采用.

在ΔABC中，记

(1)

则由Gerretsen不等式和三角形基本不等式以及Euler不等式知x≥0,y≥0,z≥0,u≥0.如果一个不等式能够用x,y,z,u非负表示出来，就可以实现对这个不等式的证明，这便是s,R,r分拆证明的基本思路.

以下约定：ΔABC三边为a,b,c，半周为s，角平分线、类似中线、高分别为wa,wb,wc、ka,kb,kc和ha,hb,hc，内切圆和外接圆半径分别为r和R.用∑和∏分别表示循环和与循环积.

1　一些常用的分拆单元

要实现一个半正定式的非负分拆证明，首先需要构造一些基本的非负分拆单元(或分拆基，分拆项等).(1)式中的x,y,z,u就可以看作是基本分拆单元.

1.1杨学枝不等式

杨学枝在文献[4]中提出并证明了不等式

(2)

显然，不等式(2)强于Gerretsen不等式.容易证明

(2′)

即这里给出了不等式链(2)的一种证明.可以看出，m和n是比较强(小)的分拆单元.

1.2强于Gerretsen不等式的分拆单元

其中

e=-s2+2(R-2r)s+r(7r+10R),f=-s2-4(R-2r)s+12R2-5r2-8Rr.

可以看出，e和f也是一组很强的分拆单元，且次数仅仅是2次.

常见的有2个，分别为

(3)

注意(3)式中第2个分拆单元q要强一些.如果拆较弱的不等式，则用分拆单元p即可.

1.4正的分拆单元

在构造分析表达式时，有时候需要一些正的几何量的参与.如在锐角三角形不等式中有正的量s-2 R-r，这是因为有条件不等式

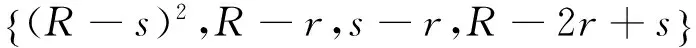
1.5锐角三角形中的分拆单元

在锐角三角形中，除过上述提到过的分拆单元v之外，还有walker不等式

w=s2-2R2-8Rr-3r2≥0.

(4)

对锐角三角形，分拆单元w是一个首选的分拆单元.注意到

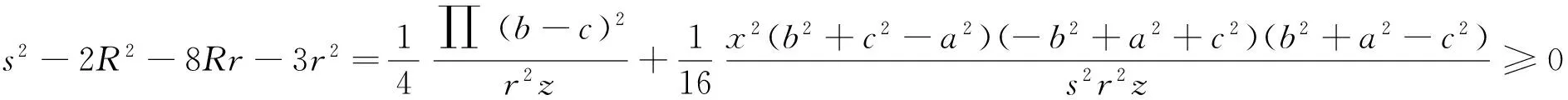
另外，不等式(4)有加强式

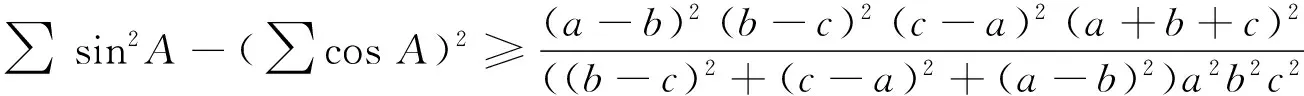
s4-(2r2+20Rr+3R2)s2+r(5r+11R)(4R+r)(r+R)≥0.

(5)

这个分拆单元可用于更强的锐角三角形不等式的证明，(5)式容易证明.

1.6含参分拆单元

当t∈R时，有含参分拆单元

2Rr2(16R2+8Rr+r2-3s2)t2+2r(s4+(-18Rr-8R2+2r2)s2+

r(6R+r)(4R+r)2)t+(4r+2R)s4-4r(12R2-2r2+19Rr)s2+2r2(9R+2r)(4R+r)2≥0

这个关于t的二次不等式的判别式为Δ=-∏(b-c)2(∑bc)2≤0，由此容易获证.

还有一些其他分拆单元.如(3)式有加强不等式

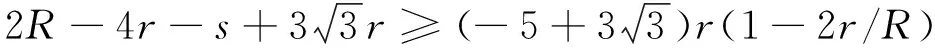
此不等式可由杨学枝不等式推出.用此分拆单元可分拆一些更强的不等式.

事实上，只要获证的关于s,R,r的不等式均可作为分拆单元.由此可见，分拆单元是开放的.虽然如此，一般情况下还是要尽量地少引入新的分拆单元，除非用上面常用的分拆单元拆不出来的时候，才考虑去扩充它.

2　分拆算法

2.1分拆命令

关于s,R,r不等式的分拆算法文献[2]曾介绍过，并编写了程序tganyfc，它调用了解线性方程组非负解程序lpaolve[5].tganyfc的命令格式是：

>tganyfc (d,ex);

功能是以数据集d为基本项(基本项等具体概念参阅文献[6])，对表达式ex进行分拆.

除tganyfc命令外，还有命令zktganyfc，这个命令主要是在附加项中引入了非负表达式，以补充附加项中出现负系数的情况.命令格式是：

>zktganyfc(d,ex,bc);

功能是以数据集d为基本项，将bc补充到附加项，对表达式ex进行分拆.

bc可由grbc函数产生，也可通过对数据进行各种运算产生.

2.2数据构造

考虑到s,R,r均是对称量，故本文中的数据构造较为简单，就是通过文献[7]介绍的取积重数函数qjcss构造分拆集.qjcss命令的Maple程序如下：

qjcss∶=proc(czset,t)forifrom1totdotemp∶=tempunionlbxcun(temp,czset)od;locali,temp;temp∶=tempminus{1};temp∶={1};returntemp;end:

从这段程序可以看出,qjcss的含义是：对一个数据集czset进行累积，将每次乘的结果收集起来，得到一个数据集，其中变参t表示累计乘积的重复次数(重数).

例1键入命令qjcss({a, b, c}, 1)，输出{a,b,c}.键入命令qjcss({a, b, c}, 3)，输出{a,b,c,a2,a3,b2,b3,c2,c3,ab,ac,a2b,a2c,bc,bc2,b2a,b2c,c2a,abc}.

用qjcss命令构造好数据集，就可以调用tganyfc进行非负分拆了，程序如下：

1.sRrfc∶=proc(ex,sset,t);4.dd∶=glld(gldeg(dd,degree(ex)));2.localdd,ls;5.ls∶=tganyfc(dd,ex);3.dd∶=qjcss(sset,t);6.returnls;end:

其中语句3～4实现分拆数据的构造；语句5调用tganyfc实现非负分拆.

sRrfc就是本文反复使用的分拆命令，这个命令有3个输入参数：ex表示一个关于s,R,r的多项式；sset是由分拆单元构成的数据集；t是取积重数.由于数据集的选取是不完整的，故这里的算法是一个试探性算法，不是总会分拆成功的.

3　应用举例

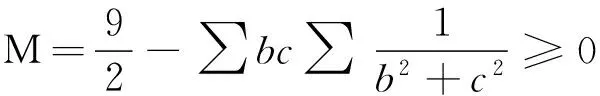
证键入命令:

>tosRrw(M);# tosRrw的作用是将三角形中的对称表达式用s,R,r表示出来#

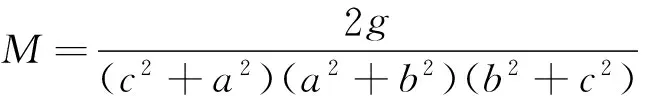
g=2s6-r(-5r+44R)s4+4r2(55R2-r2+12Rr)s2-7r3(4R+r)3≥0.

接着键入命令sRrfc(f, `union`(gr[2]), 2)，则输出

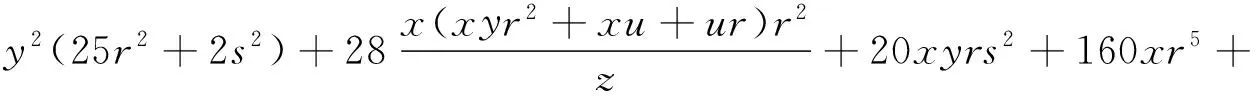
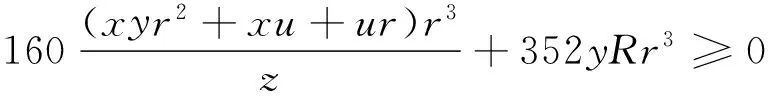
g2=y2(25r2+2s2)+28xmr2+20xyrs2+160xr5+160mr3+352yRr3≥0.

由(1)～(4)式中的不等式知，g≥0成立，由此得证.

注1由例2知，s,R,r分拆结果可以有g1和g2两种表示形式，即单纯用x,y,z,u表示的形式和用x,y,z,u外加其他不等式表示的形式.一般来说，采用g1的表示形式更直观一些，但表达式却较繁琐；g2的形式虽然简洁但却引入了较多的不等式.究竟采用何种表示形式，取决于个人爱好和问题的需要.

例3在ΔABC中，证明不等式:4∑(cos A+sin 2A)2cos2A≥∑(cos A+sin A)2.

证易证不等式等价于

g=s6+2Rs5+(-7R2-15r2-12Rr)s4-4(4R2+5r2+5Rr)s3R+

(8R4+56R3r+114R2r2+72Rr3+15r4)s2+2(16R4+46R3r+5r4+64R2r2+30Rr3)sR-

r6+18R6-120R3r3-12Rr5-120R4r2-55R2r4-32R5r≥0.

键入命令

>d∶=glld(qjcss(gr[2] union grbc(1,1),2));

>elpsolvetg(d,g);

输出分拆式

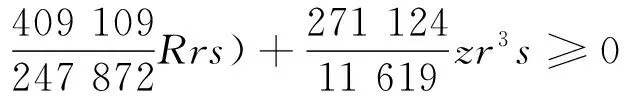
注2在例3中，由于g是一个s的奇、偶次交替且次数较高的不等式，分拆难度甚大，但这里用函数grbc生成正的数据以补充附加项，从而使问题容易求解了.

证由于所给不等式含有根式型几何量wa，故可用agl2012程序的subs(lsta,ex)命令将不等式等价地化为锐角三角形中的不等式进行证明(本质上是做了角代换).

A→π-2A,B→π-2B,C→π-2C.

(6)

容易证明，所给不等式等价于锐角三角形中的不等式Q≥0(具体表达式略).由命令

>sRrfc(Q, `union`(gr[2],{jb,v}), 2);

可将Q分拆为

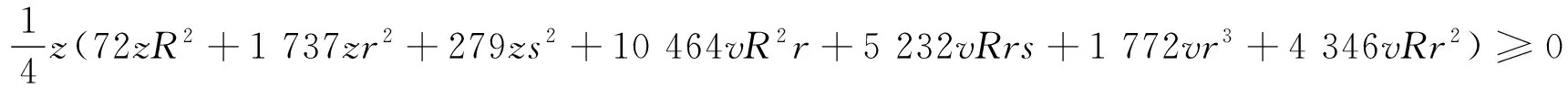
在例4中，由于涉及到了锐角三角形，故数据集中用了锐角数据v=s-2R-r.

类似于例4的方法，可证明如下ΔABC中优美且难度甚大的不等式.

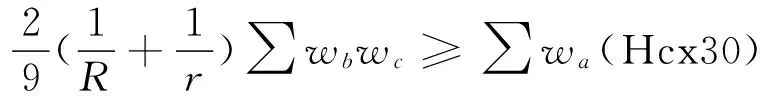
对于s次数较高的情况，此时分拆表达式中每个分拆项中会有较多的待定变量.如果再按所构造数据的全集去分拆，势必会造成变量太多而导致分拆失败.为了解决这个问题，可以将构造的数据集分割成若干子集，对这些子集按某种条件进行选择，再尝试着用子集进行分拆.虽然此时分拆的效率会大打折扣，但可以解决较复杂的问题，并可能得到多种分拆解.

证用tosRrw命令容易得到

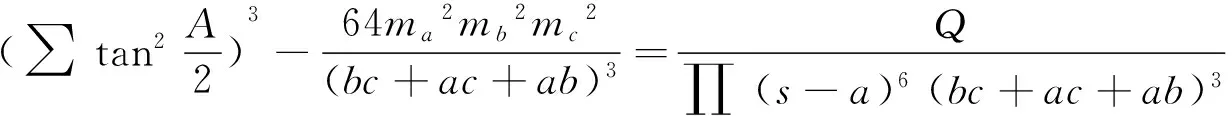
Q中s的次数高达12次.键入命令：

>with(combinat, choose);#调入Maple函数库，为计算子集做准备#

>ld ∶= choose(d) minus {{}};#d是构造好的数据集，用choose 计算出d的所有子集#

>lv∶=gldeg(ld,4);#挑选出元素个数为4的子集参与分拆#

这样可得到若干分拆式，具体分拆表达式此略.

下面举2个条件分拆的例子，这类分拆可以部分解决一些难度较大的根式型不等式.

例6网友Mateescu Constantin在2016年4月8日给笔者来信中提出讨论不等式:

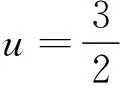
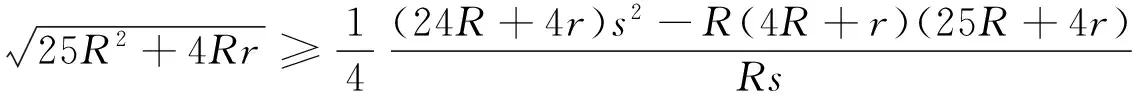
令λ=(24R+4r)s2-R(4R+r)(25R+4r)，如果λ≤0则不等式成立；如果λ≥0，则

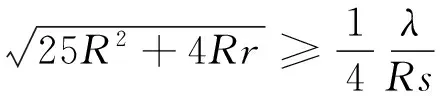
但g有分拆式

147(R-2r)(4R2+4Rr+3r2-s2)R+117(4R2+4Rr+3r2-s2)R2≥0.

例7在ΔABC中，证明不等式

∑(cos A+sin A)2sin A≥∑(cos A+sin B)(cos B+sin A)sin C.

证易证不等式等价于

5rs2+4(R-2r)sR-3r(2R+r)(4R+r)≥0⟺

4(R-2r)sR≥r(-5s2+24R2+18Rr+3r2).

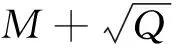
目前，多项式的配平方和已经取得了一些进展[5-7,11-12].但当次数较高时配方会遇到麻烦，主要问题是当次数高时配方时间较长，或者配不出来.此时可将多项式不等式化为关于s,R,r的不等式解决.由于可以缩短配方时间，故这种思路对海量筛选不等式结果有意义.

例8证明文献[13]中的不等式(6)(注意这里x,y,z≥0，与(1)式中的含义不同)

(xy2+yz2+zx2)(x2y+y2z+z2x)≥(x+y+z)(x2+y2+z2)xyz.

证用xtos和tosRrw命令易将题中所给代数不等式转化为等价的三角形中的不等式：f=(5r-16R)s2+(4R+r)3≥0，这个不等式次数仅是3次，很容易分拆证明.

在实际应用中，到底是采用代数的方法还是s,R,r分拆的方法解决问题，需要根据实际情况而定.

证此不等式化为s,R,r表达式时，次数高达14.而代数化后，仅是9次.用agl2012程序的elpsolvesgm命令易得到配平方和(具体配方式此略)

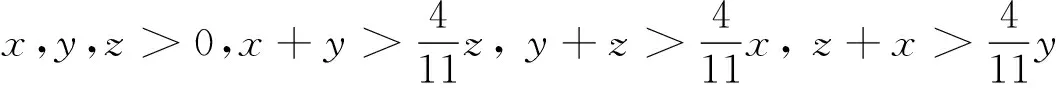
(7)

注意这里的x,y,z含义与(1)式不同.

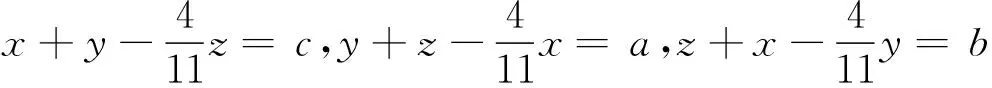
将x,y,z的表达式代入(7)式，整理得一个3元6次多项式不等式f(a,b,c)≥0，这个关于正数a,b,c的代数不等式，由于系数较大，不容易对其进行配平方证明，但化为三角形中的几何不等式后容易分拆证明，具体过程此略.

在确定三角形几何量的量级时，s,R,r分拆方法起着十分关键的作用.

4　角代换可扩展不等式

设ΔABC中，有仅涉及三角形内角A,B,C三角函数的不等式

f0=f(A,B,C)≥0.

(8)

对不等式(8)作角代换(6)得不等式

f1=f(π-2A,π-2B,π-2C)≥0.

(9)

如果不等式(9)在ΔABC中仍然成立，则称不等式(9)为不等式(8)的1级角代换扩展不等式，称不等式(8)为1级角代换可扩展的，记作f1=φ(f0)=φ(f(A,B,C)).

如果不等式(9)仍然是角代换可扩展的，即对不等式(9)作角代换(6)，得到不等式

f2=φ(f1)=φ(φ(f0))=φ(φ(f(A,B,C)))≥0.

(10)

则称不等式(10)为不等式(8)的2级角代换扩展不等式，称不等式(8)为2级角代换可扩展的.这样就可以定义多级角代换扩展不等式.

例12网友Nguyenhuyen_AG提出Gerretsen不等式4R2+4Rr+3r2-s2≥0的等价不等式

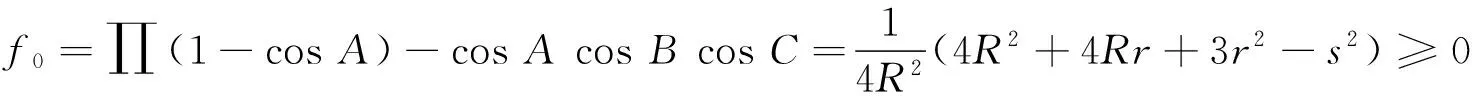
试验证不等式f0≥0是3级角代换可扩展的.

解用Bottema软件容易验证，有不等式

φ(f0)=∏(1+cos 2A)+∏cos 2A=

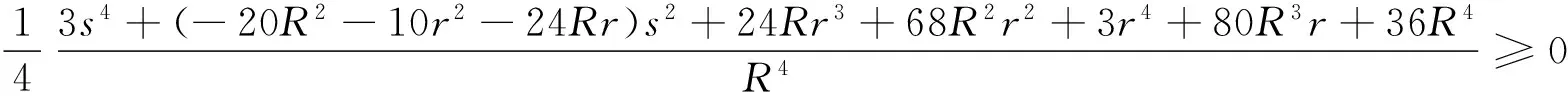
φ(φ(f0))=∏(1+cos 4A)+∏cos 4A≥0,

φ(φ(φ(f0)))=∏(1+cos 8A)+∏cos 8A≥0,

故f0是3级可扩展的.由φ(f0)≥0可得优美且很强的不等式

3s4+(-20R2-10r2-24Rr)s2+24Rr3+68R2r2+3r4+80R3r+36R4≥0.

同理验证有角代换可扩展不等式

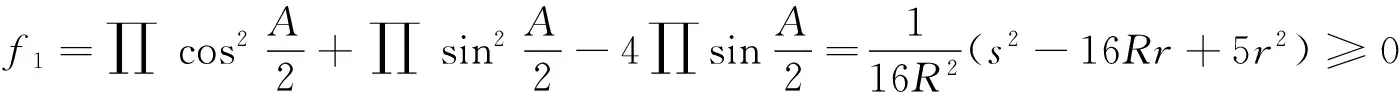
有趣的问题是：在例12中，是否有θ(f0)=∞,θ(f1)=∞,即f0和f1是否为无穷级角代换可扩展不等式？

在角代换可扩展不等式研究中要注意排除平凡的情形，挑出强而有价值的不等式进行研究.在agl2012程序中，有专门的验证角代换可扩展不等式命令，如gljdhkz2可验证一个不等式是否为2级可扩展的，gljdhkz3可验证一个不等式是否为3级可扩展的，这样结合不等式自动发现命令，就可以十分方便地自动发现角代换可扩展不等式.

例13在agl2012程序的运行环境中，键入命令:

>d0∶=gldc3(tosgm(qjcs(qhcs(bc3g({cos(A)}),1),3)));#准备关于三角形内角余弦的数据#

>zjbj_otfqdcs(d0,d0,0,0,1,1,1);#调用自动发现命令在数据d0的构成环境中搜索不等式#

>gljdhkz2(jg);#对上述产生的不等式集jg进行分析，挑出2级角代换扩展不等式#

这样可输出数百个角代换可扩展不等式，如有优美结果(杨学枝不等式的等价式)

f0(A,B,C)=∑(cos B+cos C)2-2∑(cos A+cos B)(cos A+cos C)cos A=

考虑这个不等式的角代换扩展不等式，有

f1(A,B,C)=φ(f0(A,B,C))=f0(π-2A,π-2B,π-2C)=

∑(cos 2B+cos 2C)2+2∑(cos 2A+cos 2B)(cos 2A+cos 2C)cos 2A≥0⟺

-s6+(10R2+7r2+12Rr)s4+(-32R4-88R2r2-80R3r-7r4-40Rr3)s2+

192R4r2+12Rr5+58R2r4+128R5r+144R3r3+r6+36R6≥0,

f2(A,B,C)=φ(f1(A,B,C))=φ(φ(f0(A,B,C)))=f1(π-2A,π-2B,π-2C)=

∑(cos 4B+cos 4C)2+2∑(cos 4A+cos 4B)(cos 4A+cos 4C)cos 4A≥0.

注3在角代换不等式序列中，t-1级角代换扩展不等式ft-1≥0总是t级角代换扩展不等式ft≥0的推论，这是因为(6)式的反变换是

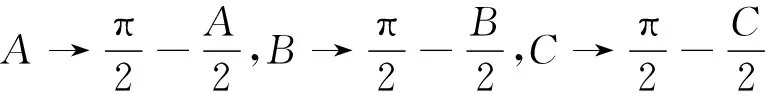
(11)

变换(11)恰好构成一个三角形(设这个三角形为S)的三个内角，这相当于对三角形S应用ft≥0得到ft-1≥0.故角代换扩展不等式序列是一个强度不断增强的不等式序列.

进一步研究角代换可扩展不等式的分布和性质很有趣.

[1] 刘保乾.随机数验证程序在多项式非负分拆中的应用[J]. 汕头大学学报，2012，27(3)：27-37.

[2] 刘保乾，磨光集及其应用[J]. 汕头大学学报，2015,30(2):44-55.

[3] 刘保乾.不等式的自动发现原理及其实现[J].汕头大学学报，2011，26(2)：3-11.

[4] 杨学枝.一类不等式的统一证法·数学竞赛(19)[M].长沙：湖南教育出版社，1994.

[5] 隋振林.一个求线性方程组非负解的通用程序[J] . 广东第二师范学院学报，2014,34(3):32-35.

[6] 刘保乾. 多项式非负分拆算法的若干改进和补充[J].汕头大学学报，2013，28(3)：18-28.

[7] 刘保乾. 两组变元多项式的平方分解[J]. 广东第二师范学院学报，2013，33(5):25-32.

[8] 刘保乾.Bottema,我们看见了什么―三角形几何不等式研究的新理论、新方法和新结果[M].拉萨:西藏人民出版社，2003:360-367.

[9] 尹华焱.100个涉及三角形Ceva线、旁切圆半径的不等式猜想[M]//杨学枝. 不等式研究(第1辑)，拉萨:西藏人民出版社，2000:313-322.

[10] 刘保乾.带约束条件多项式的差分代换及应用[J].汕头大学学报，2010. 25(2):4-10.

[11] 李轶.一类半正定多项式的配平方和算法[J].系统科学与数学，2008,28(4):490-504.

[12] 何灯.一类三元对称分式的平方型分拆及其程序实现[J].汕头大学学报,2011,26(1):35-42.

[13] 刘保乾. 不等式自动发现与判定程序agl2012典型应用9例[J]. 广东第二师范学院学报，2016，36(3)：13-22.

[14] 刘保乾.用对称性和量级研究三角形中的非负对称量[M]//杨学枝. 不等式研究(第1辑)，拉萨西藏人民出版社，2000:200-222.

The Rediscovery of the Proof Based on Decomposition Involvings,Randrin Triangle Geometric Inequality

LIU Bao-qian

(Tibet Autonomous Region Information Management Center of Authorized Strength’s Organization, Lhasa, Tibet, 850000, P.R.China)

This paper is posed to discuss the proof based on decomposition involvings,Randrin triangle geometric inequality， and to research the method and program for decomposition. A large number of examples show that, although it is only tentative, it can easily solve some of the more difficult problems. The radical inequalities problem is solved by means of non negative decomposition with constraint conditions. There is a new proof for Yang Xue-zhi’s Inequality and Walker’s Inequality in this paper. Extensible inequality with angular substitution is posed and preliminarily discussed.

triangle geometric inequality; extensible inequality with angular substitution; non negative decomposition; mechanical theorem proving

2016-07-20

刘保乾，男，陕西凤翔人，西藏自治区组织编制信息管理中心工作人员.

O 122.3

A

2095-3798(2016)05-0029-09