具有有界二阶导数的函数的分数阶不等式

时统业，夏　琦，王　斌

(1.海军指挥学院 信息系， 江苏 南京 211800;2.海军蚌埠士官学校 航海系， 安徽 蚌埠 233012)



具有有界二阶导数的函数的分数阶不等式

时统业1，夏琦1，王斌2

(1.海军指挥学院 信息系， 江苏 南京 211800;2.海军蚌埠士官学校 航海系， 安徽 蚌埠 233012)

建立了一个分数阶积分的恒等式，利用它得到具有有界二阶导数的函数的一些不等式．

二阶导数；分数阶积分；积分不等式.

0　引言

定义1[1]设f(x)在区间I上有定义，f(x)在I上称为是凸(凹)函数，当且仅当：对任意x1，x2∈I，λ∈(0，1)，有f(λx1+(1-λ)x2)≤(≥)λf(x1)+(1-λ)f(x2)．

设f(x)是[a，b]上的凸(凹)函数，则有

(1)

Dragomir S S和Agarwal P在文献[2]中证明了h(a，y)、H(a，y)在[a，b]上关于y单调增加．

王良成在文献[3]中给出式(1)的如下推广：

定理1[3]设f是[a，b]上的连续凸函数，p∈(0，1)，ξ=pa+(1-p)b，则

(2)

由式(2)可生成两个二元函数，即对任意x，y∈[a，b]，x≤y，t∈(0，1)，定义

与式(2)有关的文献可见文献[4-9]，其中，王良成在文献[4-5]中证明了h(x，b)、H(x，b)、h(t；x，b)和H(t；x，b)在[a，b]上关于x单调减少，h(t；a，y)和H(t；a，y)在[a，b]上关于y单调增加．文献[6]证明了h(t；x，y)和H(t；x，y)的准线性，文献[7]在一阶导数有界的情况下给出h(t；x，y)的上界．

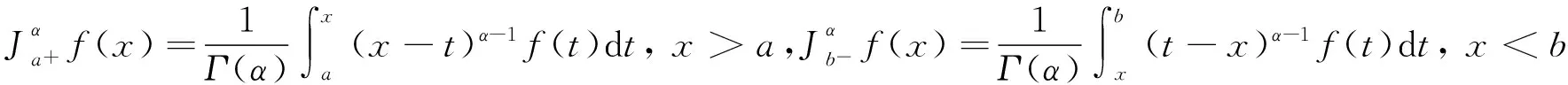
关于Riemann-Liouville分数阶积分的性质及应用可参阅文[10-14]及其引用文献．文献[15]首先建立了涉及Riemann-Liouville分数阶积分的Hermite-Hadamard型不等式：

定理2[15]设f是[a，b][0，∞)上的正值函数且在[a，b]上勒贝格可积．α>0.若f是[a，b]上的凸函数，则有

(3)

当α=1时由式(3)可得式(1)．文献[16]考虑由式(3)的两端生成差的界，给出下面结果：

定理3[16]设f是[a，b]上的正的二阶可微的函数，且在[a，b]上勒贝格可积．若f″在[a，b]上有界，则有

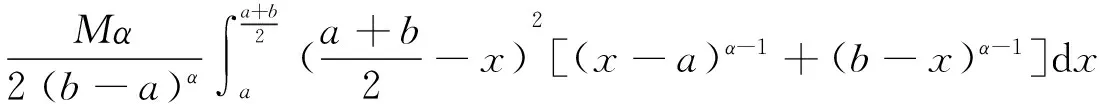
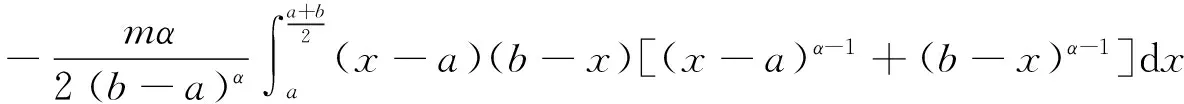
其中α>0，m=inft∈[a,b]f″(t)，M=supt∈[a,b]f″(t)．

本文的目的是首先将不等式(2)推广到Riemann-Liouville分数阶积分，然后在二阶导数连续的条件下考虑生成差的界．为方便起见，引入下面记号：

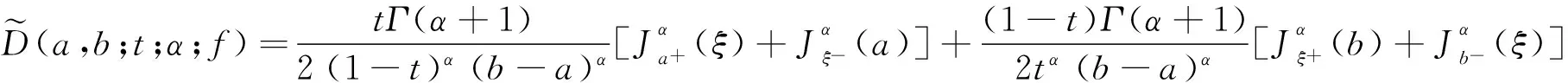
1　引理

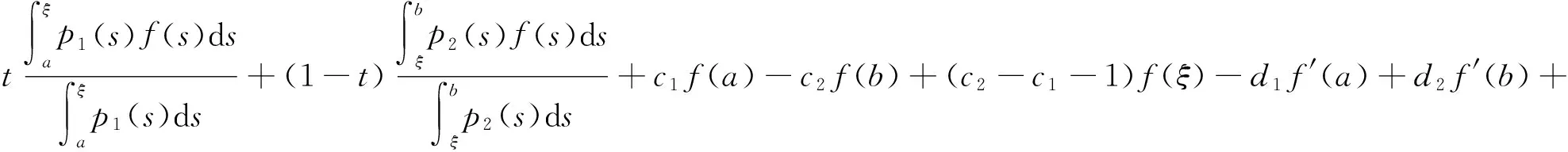
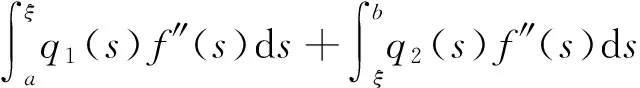
(4)

其中

证明利用分部积分法得

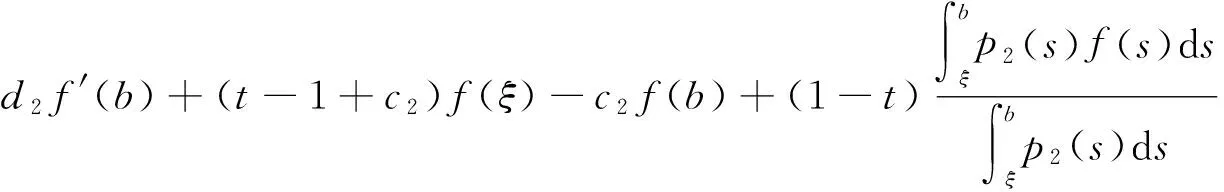
将上面两式相加即得式(4)．

引理2设f在[a，b]上具有二阶连续导数，t∈(0，1)，c1，c2，d1，d2是常数，α>0，则

(5)

其中

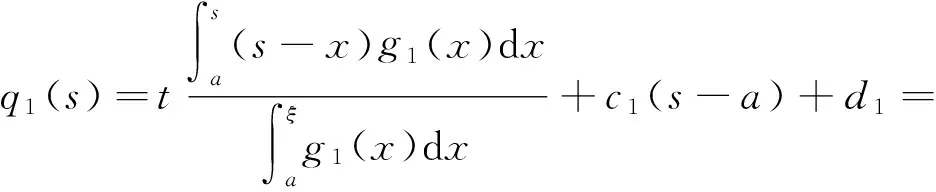
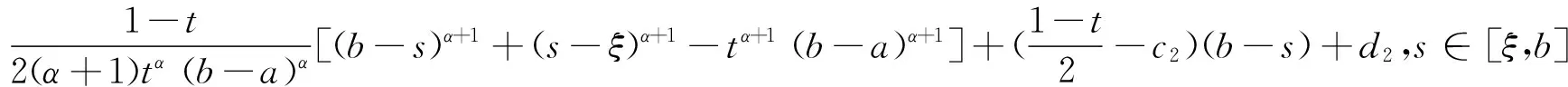
g1(x)=(ξ-x)α-1+(x-a)α-1，g2(x)=(b-x)α-1+(x-ξ)α-1．

由式(4)得到式(5)．

2　主要结果

定理4设f是[a，b]上的正值函数，t∈(0，1)，ξ=ta+(1-t)b，α>0．若f是[a，b]上的凸函数，则有

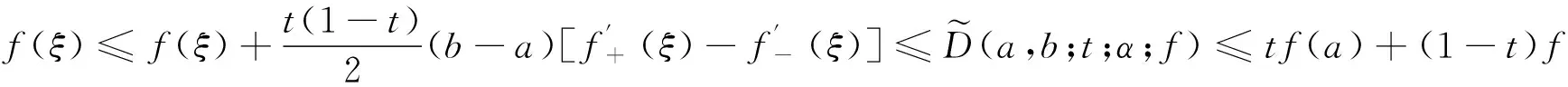
(6)

证明因为f是[a，b]上的凸函数，所以对于任意x∈[a，b]，有

(7)

(8)

将式(7)和(8)分别乘以(ξ-x)α-1+(x-a)α-1、(b-x)α-1+(x-ξ)α-1，然后分别在[a，ξ]和[ξ，b]上对x积分得

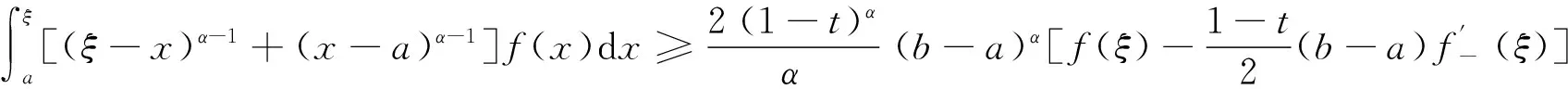
(9)

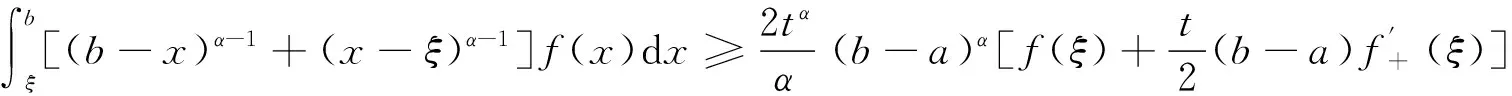
(10)

(11)

(12)

定理5设f在[a，b]上具有二阶连续导数，t∈(0，1)，α>0，则有

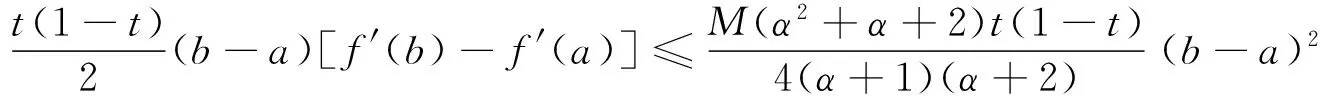
(13)

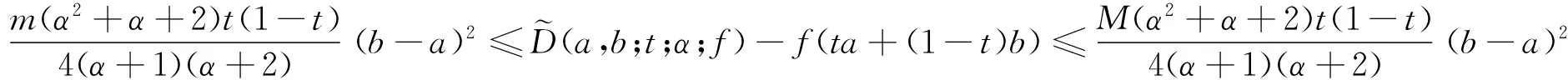
(14)

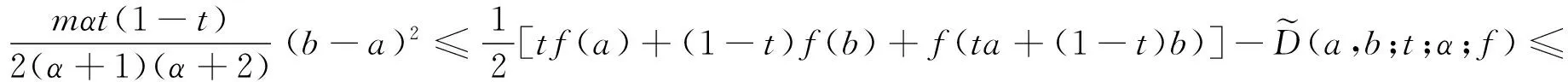
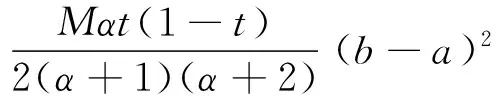
(15)

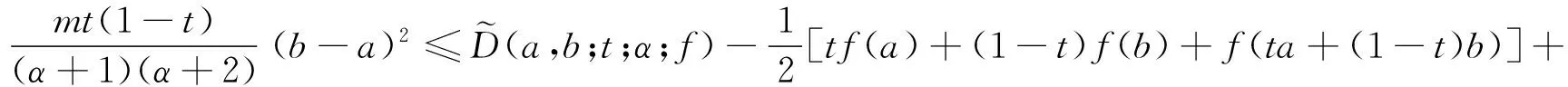
(16)

(17)

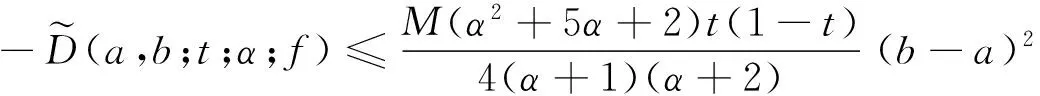
(18)

其中

m=inft∈[a,b]f″(t)，M=supt∈[a,b]f″(t)．

其中

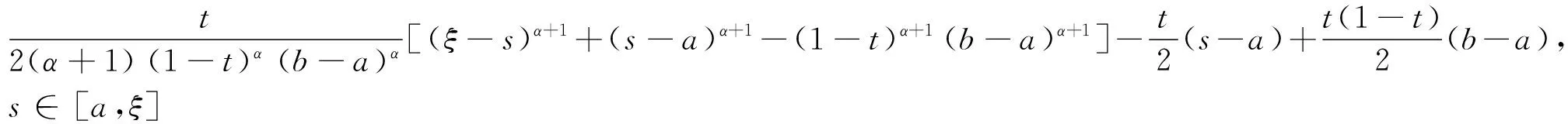
式(13)的右端得证，同理可证式(13)的左端，因此式(13)得证．

推论1设f在[a，b]上具有二阶连续导数，t∈(0，1)，则有

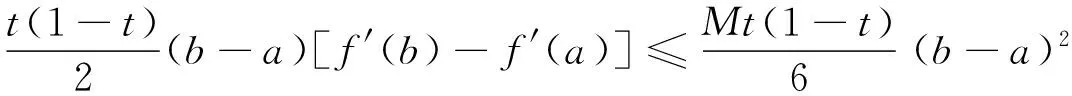
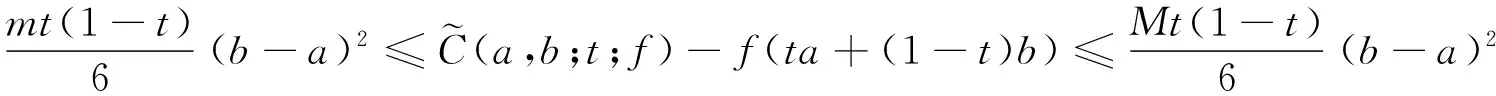
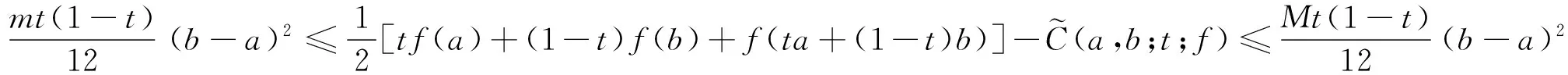
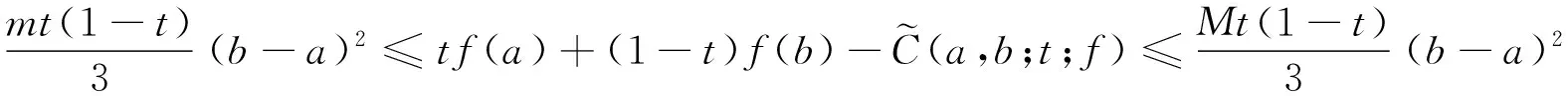
证明在定理2中取α=1即可得证．

[1] 裴礼文．数学分析中的典型问题与方法[M]．2版．北京：高等教育出版社，2006：268.

[2]DRAGOMIRSS，AGARWALP．TwonewmappingsassociatedwithHadamard’sinequalitiesforconvexfunctions[J]．ApplMathLett，1998，11(3)：33-38．

[3] 王良成．凸函数的Hadamard不等式的若干推广[J]．数学的实践与认识，2002，32(6)：1027-1030．

[4]WANGLiangcheng．OnextensionsoftwomappingsassociatedwithHermite-Hadamardinequalitiesforconvexfunctions[J]．PublikacijeElektrotehnickogFakulteta-Serija：Matematika，2006，17：8-17．

[5]WANGLiangcheng．SomerefinementsofHermite-Hadamardinequalitiesforconvexfunctions[J]．PublikacijeElektrotehnickogFakulteta-Serija：Matematika，2004，15：39-44．

[6] 郭凤云．浅析凸函数的Jensen不等式的应用[J]．中国科教创新导刊，2011，26：95-96．[7] 赵伟珍，李爱军．凸函数的一个Hadamard型不等式[J]．安徽广播电视大学学报，2007(1)：123-124．

[8] 于永证，刘证．另一个新的与Hadamad不等式相关的映射[J]．纯粹数学与应用数学，2008，24(3)：547-550．[9] 邓志颖，刘祥清，沈世云．GA-凸函数的Hadamard型不等式的改进和应用[J]．数学的实践与认识，2012，42(20)：201-207．

[10] GORENFLO R, MAINARDI F. Fractional calculus, integral and differential equations of fractional order[M]. Wien：Springer，1997.

[11] 武女则．分数阶导数、积分的性质及几何意义[J]．哈尔滨师范大学学报(自然科学版)，2013，29(1)：19-22．[12] 武女则．分数阶导数和积分的奇偶性及周期性[J]．山东理工大学学报(自然科学版)，2013，27(3)：51-54．

[13] 杨小军，高峰，钟卫平，等．分数阶定积分学[J]．世界科技研究与发展，2008，30(5)：636-638．

[14] 祝奔石．分数阶微积分及其应用[J]．黄冈师范学院学报，2011，31(6)：1-3．

[15] SARIKAYA M Z，SET E，YALDIZ H，et al．Hermite-Hadamard’s inequalities for fractional integrals and related fractional inequalities[J]．Mathematical and Computer Modelling，2013，57(9-10)：2403-2407．

[16] CHEN feixiang．Extensions of the Hermite-Hadamard inequality for convex functions via fractional integrals[J]．Journal of Mathematical Inequalities，2016,10(1)：75-81．

Fractional Integral Inequalities for Functions with Second Derivatives Bounded

SHI Tong-ye1, XIA Qi1, WANG Bin2

(1. Department of Information, PLA Naval Command College, Nanjing, Jiangsu, 211800, P.R.China; 2. Department of Navigation, PLA Bengbu Naval Petty Officer Academy, Bengbu, Anhui, 233012, P.R.China)

A general identity for fractional integrals is derived. Using this identity, some integral inequalities for functions whose second derivatives are bounded are established.

second derivative; fractional integral; integral inequality

2015-12-09

时统业，男，河北张家口人，海军指挥学院信息系副教授.

O178

A

2095-3798(2016)05-0043-06