一种基于谱聚类的社交关系数据处理方法

吴陈，朱晨

（江苏科技大学 江苏 镇江212000）

一种基于谱聚类的社交关系数据处理方法

吴陈，朱晨

（江苏科技大学 江苏 镇江212000）

随着社交应用软件的广泛普及，社交关系数据中存在的价值得到人们的广泛关注，社交关系网络可以抽象成一种图结构，将用户从关系结构上进行划分等价于对图进行分割。针对NJW多路谱聚类算法在处理图分割时需要人为确定聚类数目的问题，引入本征间隙的方法，通过对输入样本数据的拉普拉斯矩阵进行谱分析，得出样本的聚类数目。实验证明，改进后的NJW算法，在实验数据集上可以自动获取聚类数目并具有较好的聚类效果。

谱聚类；NJW；本征间隙；K-means

随着互联网行业的蓬勃发展，各种社交应用积累了无数的用户关系数据，海量社交数据的背后存在着巨大的价值，将用户群体从结构上进行划分，是所有社交应用研究人员关注的主要内容。想要从传统的使用二维表记录的用户数据中发现用户关系，可以使用嵌套的sql查询语句方式得到，但是多层嵌套的sql语句运行的效率不佳。社交关系数据本质上是一个无边际的网络，网络中的结点代表用户，结点之间的边代表用户之间的关系，这种社交关系结构符合复杂网络中的自组织、自相似、吸引子、小世界、无标度的特性。如何快速地从社交关系结构上将用户分开，是如今很多学者研究的方向。将用户从关系结构上进行划分，可以看作是对图进行分割。图分割问题本质上是一个NP难问题，可以通过求取关系图的相似度矩阵或Laplacian矩阵的谱分解来转化它。

NJW算法是一种多路谱聚类算法，但在进行聚类之前仍然需要人为确定聚类数目。针对这一问题，通过对样本数据建立相似矩阵并进行谱分析，从最大本征间隙所在的位置获得聚类数目，将本征间隙与NJW算法结合，改进后的NJW算法可以自动获取聚类数目，并在实验数据上获得了理想的聚类效果。

1 谱图理论与谱聚类算法

图是由结点（Vertices）和边（Edge）构成，可以表示为G=（V，E），其中V（G）是图中结点的非空点集，V（G）中元素的无序对构成边集合E（G）。V（G）中元素称为顶点或结点，通常表示为V=｛v1，v2，…，vn｝，其中结点的个数用n（G）=|V|表示。E（G）中的元素称为边，通常使用（vi，vj）表示结点vi和vj间相连的边，边数用m（G）=|E|表示。当vi∈V（G）称为结点vi的度。

图G的特征值即为图G的邻接矩阵W（G）的特征值。对于一个有n个结点的无向图来说W（G）是一个n阶实对称阵，必有个特征值，并且这些特征值都是实数。用λi=（i=1，2，…，n）表示W（G）的n个特征值。邻接矩阵W（G）的n个特征值λi=（i=1，2，…，n）组成的有序序列即为图的谱。

由于社交关系数据中没有具体的坐标值，因此不能直接使用欧几里得距离等度量算法来对数据进行聚类［1］，对图结构数据进行聚类主要通过谱聚类算法。

谱聚类（Spectral clustering）算法是一种图分割算法，其思想来源于谱图划分理论［2］，与传统的聚类算法相比，它具有在任意形状的样本空间上聚类且收敛于全局最优解的特点，并且在解决非块状、非凸球形数据的聚类问题时有着十分出色的表现［3］。

谱聚类算法的一般过程可以归纳为如下形式W：

1）根据选用的相似性度量方法，构建样本数据的相似矩阵；

2）计算相似矩阵W的度矩阵D；

3）计算拉普拉斯矩阵L=D-W；

4）计算拉普拉斯矩阵L特征值与特征向量；

5）将样本数据构成的点集映射到基于一个或多个特征向量确定的低维空间中；

6）在低维空间中，将数据集按行划分到两类或多类。

相似矩阵又称亲和矩阵，通常使用A或W来表示，该矩阵中的元素，其定义为：

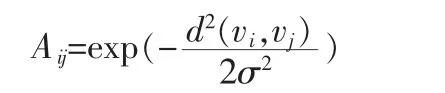
其中d（vi，vj）表示样本点 i与 j之间的距离，欧式距离‖vi，vj‖表示。σ是尺度参数 ，决定了样本点之间相似性的缩放程度。将相似矩阵中每行元素值相加，即得到该样本点的度。从样本结点的度中可以找到该样本点周围其他结点的分布情况。所有样本点的度值构成的对角矩阵，称为度矩阵，D用表示，

常见的图划分准则有最小割集准则（Minimum cut）［4］，规范割集准则（Normalized cut）［5］，比例割集准则（Ratio cut）［6］，平均割集准则（Average cut）［7］，最小最大割集准则（Min-max cut）［8］。拉普拉斯矩阵主要有两种形式，即规范化拉普拉斯矩阵和非规范化拉普拉斯矩阵，规范化拉普拉斯矩阵是通过松弛Ncut得到，非规范化拉普拉斯矩阵是通过松弛RatioCut得到［9］。

非规范化拉普拉斯矩阵可以表示为L=D-A，并具有如下特性：

2）L是半正定矩阵；

3）L中存在0特征值，并且0特征值对应的特征向量所含元素全为1；

4）L中存在n个非负实特征值，即：0=λ1≤λ2≤…≤λn。

规范化拉普拉斯矩阵存在两种表示形式，分别为：

规范化拉普拉斯矩阵具有如下特性：

3）如果λ是Lrw的特征值，以及其对应的特征向量为，当且仅当λ和Lsym满足Lv=λDv；

5）Lrw和Lsym都是半正定矩阵，Lrw和Lsym对应的n个非负的实特征值，存在0=λ1≤λ2≤…≤λn。

文中主要采用样本数据集的规范化拉普拉斯矩阵做处理。

2 NJW算法

Ng，Jordan等人选取拉普拉斯矩阵Lsym的前k个最大特征值对应的特征向量，使其Rk在空间中构成与原数据一一对应的表述，然后在Rk空间中进行聚类［3］。

NJW算法描述如下：

1）计算矩阵Lsym的前k个最大特征值及其所对应的特征向量x1，x2，…xk，正交化处理并构造矩阵X=［x1，x2，…xk］∈Rn×k；

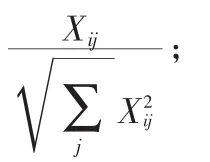
3）将矩阵Y的每一行看作是Rk空间中的一个点，对其使用k-means算法，得到k个聚类；

4）将样本点yi划分到聚类j中，当且仅当Y的第i行被划分到聚类j中。

3 本征间隙

本征间隙即相邻特征值的差值，在谱聚类算法中引入本征间隙的概念，第一个极大本征间隙出现的位置预示着聚类个数。对于有个理想的彼此分离的样本点的有限数据集来说，由该数据集构建的相似矩阵的前个最大特征值为1，而第个特征值则严格小于1，两者之间的差距取决于这个聚类的分布情况［10］。

由矩阵摄动理论可知，本征间隙越大，选取的个特征向量所构成的子空间就越稳定［11］，因此，只要找到样本数据集的相似矩阵或拉普拉斯矩阵的最大本征间隙的位置，就能确定样本数据集的聚类数目［12］，从而解决了聚类问题普遍存在的确定聚类数目的问题。再调用聚类算法，就能很快将样本点进行分类。

从本征间隙得到聚类数目算法的思路：

1）首先计算样本数据集的规范化相似度矩阵Anor；

2）计算Anor的特征值；

3）将特征值按顺序从小到大排列，即λ1≤λ2≤…≤λn；

4）计算本征间隙，得到本征间隙序列｛g1，g2，…，gn|gi=λi+1-λi｝；

5）取得本征间隙序列中第一个极大值所在的位置，即本征间隙的下标；

6）从本征间隙的下标得到聚类数目k，即k=argmin｛gi-gj|j＜i＞0∧gi-gi+1＞0｝。

求取聚类簇数目的伪代码：

输入：按从小到大排序的规范拉普拉斯矩阵的特征值

输出：输出聚类数目

｛

Max_eigengap=0

Max_eigengap_position=0

4 改进后的NJW算法

改进后的NJW算法，在输入样本数据之前，先对样本数据构建拉普拉斯矩阵 Lsym，然后对Lsym进行谱分析［13］，得出最大本征间隙所在的位置，根据最大本征间隙出现的位置自动获取聚类数目，其步骤描述如下：

1）输入样本数据计算矩阵Lsym；

2）对矩阵Lsym进行谱分析，获得最大本征间隙存在的位置，得到聚类簇数目k；

3）计算矩阵Lsym的前k个最大特征值及其所对应的特征向量x1，x2，…，xk；

5）矩阵Y的每一行看作是Rk空间中的一个点，使用kmeans算法对Rk空间聚类，得到得k个聚类；

6）将数据点yi划分到聚类j中，当且仅当Y的第i行被划分到聚类j中。

5 实验过程

本实验是在Ubuntu14.04环境下完成，使用的Python版本为 2.7.6，实验中主要引用了 Networkx，numpy，sklearn，numpy，pylab，graph_laplacian，eigsh等Python包。

文中将改进的NJW算法应用到实验数据集上得到理想的效果，使用的实验数据集如表1所示。该实验数据［15］集中包含12个用户，20条边关系。实验数据集在HuYifan比例下呈图1所示，通过观察可以发现样本数据中包含3个子图。

表1 实验实验数据集

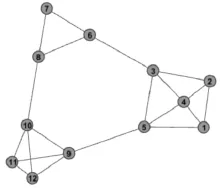
图1 样本数据集在Hu Yifan比例下的展示

图2为按从小到大排列的拉普拉斯矩阵特征值，从图2中还能看出相邻特征值之间的差值，特征值λ3与λ4之间的差值最大［14］，即最大本征间隙为 λ4-λ3，因此该样本数据集的聚类数目为3，与直接观察法得到相同结果。

最后，通过K-means算法得到实验数据集的聚类结果。如表2所示。

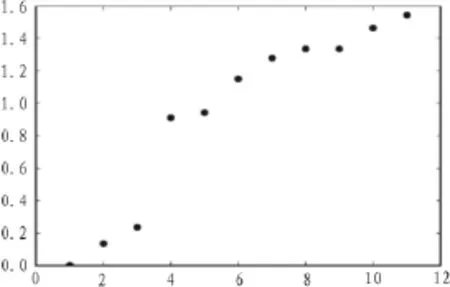
图2 本征间隙及普拉斯矩阵特征值

6 结束语

从实验结果可以看出，改进后的NJW算法能够对输入的社交关系数据自动获取聚类数目，提高了算法的自动性，并且在实验数据集上对算法行了验证，实验结果表明该算法可以有效将样本数据进行划分，保证了算法的正确性和有效性。

表2 实验数据集聚类结果

文中提出了使用谱聚类算法处理社交关系数据的方法，分析了NJW多路谱聚类算法的原理，指出其存在的不足，即聚类数目需要人为确定，提出使用本征间隙改进NJW算法，使算法可以根据输入样本数据的结构自动获取聚类数目。实验证明，改进后的NJW算法，在实验数据集上可以自动获取聚类数目并具有较好的聚类效果。

［1］温菊屏，钟勇.图聚类的算法及其在社会关系网络中的应用［J］.计算机应用与软件，2012，29（2）:161-163.

［2］Foedler M.Algebraic connectivity of graphys［J］.Czech Math，1973（23）:298-305.

［3］蔡晓妍，戴冠中，杨黎斌.谱聚类算法综述［J］，计算机科学，2008，35（7）:14-18.

［4］Wu Z，Leahy R.An optimal grapy theoretic approach to data clustering:theory and its application to image segmentation［J］.IEEE Trans on PAMI，1993，15（11）:1101-1113.

［5］Shi J，Malik J.Normalized cuts and image segmentation［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22（8）:888-905.

［6］Hagen L，Kahng A B.New spectral methods for radio cut partition and clustering［J］.IEEE Trans.Computer-Aided Design，1992，11（9）:1074-1085.

［7］Sarkar S，Soundararajan P.Supervised learning of large perceptual organization:Graph spectral partitioning and learning automata［J］.IEEE Transaction on Pattern Analysis and Machine Intelligence，2000，22（5）:504-525.

［8］Ding C，He X，Zha.Spectral Min-Max cut for Graph Partitioning and Data Mining［J］.IEEE International Conference on Data Mining，2001:107-114.

［9］严俊.谱聚类算法改进及在社交网络中的应用［D］.桂林：广西师范大学，2014.

［10］田铮，李小斌，句彦伟.谱聚类的扰动分析［J］.中国科学，2007，37（4）:527-543.

［11］孙继广.矩阵扰动分析［M］.北京:科学出版社，2001.

［12］姜慧霖.基于层次聚类的案例检索策略［J］.电子设计工程，2014，22（17）：158-161.

［13］黄婷，黄伟.基于不同算法求解子问题的Benders分解法在无功规划中的应用［J］.陕西电力，2013（3）：23-26.

［14］张伟，陈锋，马军强，等.轨/姿控发动机脉冲后效冲量快速算法的研究及应用［J］.火箭推进，2012（1）：51-56.

［15］李全鑫，魏海平.基于聚类分类法的信息过滤技术研究［J］.电子设计工程，2014，22（20）：14-16.

A processingmethod of social relational data based on spectral clustering

WU Chen，ZHU Chen
（Jiangsu University of Science and Technology，Zhenjiang 212000，China）

With the large-scaleuse ofsocialmedia applications，the value of social relationship data has drawnwide attention. The structure ofsocialnetworks can be abstracted asa graph.To divide communities from the relationalstructure isequivalent to graph segmentation.When we use NJW multiple spectral clustering algorithm to process graph segmentation issue，we need to determine the clustering numbermanually.In order to solve this problem，this paper tried to introduce the concept of Eigengap to predict the number of clusters after spectrum analysis of inputsample's Laplacianmatrix.The effectiveness of the proposed algorithm was verified with on experimentaldata and got the desired results.

spectral clustering；NJW；eigengap；K-means

TN302

A

1674－6236（2016）20-0020-04

2015-10-29 稿件编号：201510221

吴 陈（1962—），男，湖北天门人，博士，教授。研究方向：实验智能与模式识别，粗糙集理论及应用，数据挖掘与知识发现。