某型发动机风扇叶片的损伤预测与振动分析

唐　铃，尚柏林，高星伟，陈鹏飞，尹志朋

（空军工程大学 航空航天工程学院，西安 710038）

某型发动机风扇叶片的损伤预测与振动分析

唐铃，尚柏林，高星伟，陈鹏飞，尹志朋

（空军工程大学 航空航天工程学院，西安 710038）

为了延长某型发动机风扇叶片的使用寿命，其关键在于如何准确地预测产生疲劳损伤的位置以及发动机工作时可能存在的共振状态，并针对性地采取相应措施。针对这一难点，应用Ansys软件建立叶片模型，并由模态分析测试验证其合理性，在此基础上建立叶片轮盘系统模型，对系统进行静力分析和有预应力的模态分析，成功地预测了叶片产生疲劳损伤的具体位置及系统共振时的形式、临界转速及频率。结果表明：叶片轮盘系统在不同离心转速载荷下等效应力分布方式相近，无明显变化规律，且叶片产生疲劳损伤的位置均为与叶高方向垂直的耳环处，及耳环与橼板的转接处；叶片轮盘系统不可能出现高频激振力引起的共振，可能会发生低频激振力引起的共振情况，且其形式为1阶弯曲振动，转速为8 425.51 r/min，频率为567.29 Hz。

振动与波；模态分析；危险考核部位；风扇叶片；损伤预测

发动机风扇叶片在实际工作中承受着复杂的载荷，就疲劳累积损伤而言，叶片出现裂纹的部位通常为低周载荷（裂纹萌生及稳态扩展的主导）加载下等效应力最大的部位，即叶片的危险考核部位，这一部位的疲劳特性将对叶片的寿命起决定性作用［1］，为了定位某型叶片的危险考核部位，预测疲劳损伤产生的具体位置，并为发动机叶片延寿工作提供支撑，本文首先建立了叶片有限元模型，通过模态分析测试验证了模型的正确性，并在此基础上建立了叶片轮盘系统模型，通过静力分析成功锁定了叶片易出现疲劳失效的位置；另外发动机在工作时不可避免地承受着各种振动载荷，易出现叶盘共振的现象，也将对叶片的疲劳寿命产生显著性的影响［2］，通过对叶片轮盘系统施加不同的转速载荷，进行有预应力的模态分析，确定了某型叶盘系统在工作时可能引起危险共振的临界转速、发生共振时的频率以及共振时的振动形式，为后期某型发动机风扇叶片的疲劳寿命研究工作及延寿工作奠定了基础［3］。

1　叶片模态分析与测试

1.1叶片模态仿真计算

根据该型发动机风扇三级工作叶片实体，绘制三维模型并进行网格划分，网格尺寸设置为5 mm，如图1所示。设置材料参数如表1所示。

图1　叶片模型

表1　叶片材料属性

在提取叶片静态的模态参数时，可以认为叶片是一个无阻尼的自由振动系统［4］，在Ansys中，将边界条件设置为叶片所有节点外部载荷为0，两耳环的外侧面所有节点位移为0，即对其施加完全约束，进入Modal模块进行模态计算分析，提取前4阶模态，其固有频率及振型如表2所示。

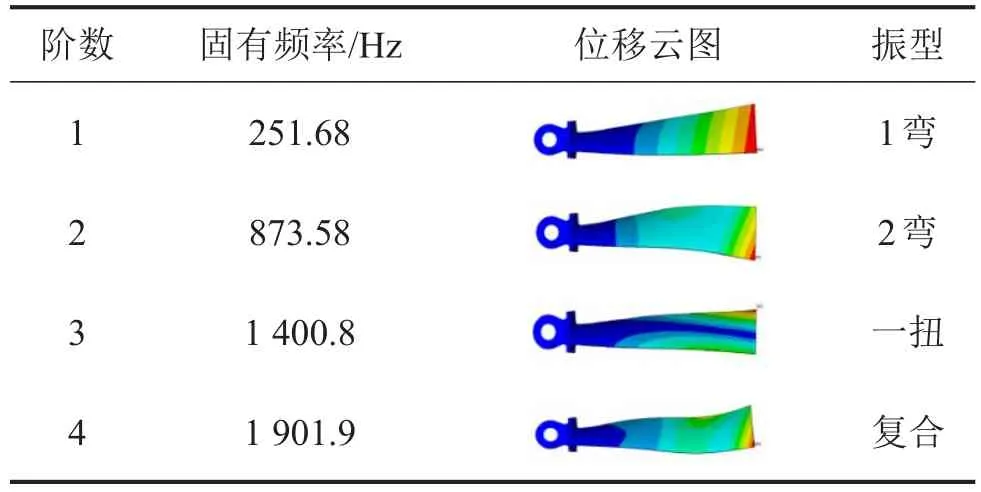
表2　模态分析结果

1.2叶片模态分析测试

1.2.1锤击法测固有频率

测量试件的固有频率常采用脉冲锤击法，它是通过带有力传感器的敲击锤对被测试件上施加一个瞬时的脉冲力，使结构产生振动响应，从而提取被测试件的各阶模态参数的一种模态测试法。此次脉冲锤击试验的系统框图如图2所示。

图2　锤击法测试系统框图

当力锤触发产生激励时，力锤及叶身上的传感器将采集力信号及振动响应信号，经过放大器放大后传输至FFT分析装置，并计算得到叶片的频率响应曲线［5］。

选取6个样品叶片，分别编号为a、b、c、d、e、f。参考叶片模态仿真计算时设置的边界条件，使用夹持装置对a号样品叶片两耳环的两个外侧面进行固定，并进行5次脉冲激励，求取5次信号响应的平均值，综合分析得到叶片的频率响应曲线如图3所示。

图3　叶片频率响应曲线

参照a号样品叶片的方式，分别对b、c、d、e四个叶片进行脉冲激励，得到各自的频率响应曲线，统计前4阶固有频率，结果如表3所示。

表3　锤击法测试结果

将所测数据求平均值，则可以认为该平均值为该型发动机风扇叶片的固有频率，即1阶固有频率f1=249.28 Hz，2阶固有频率 f2=855.99 Hz，3阶固有频率 f3=1 354.83 Hz，4阶固有频率 f4=1 851.06 Hz。

1.2.2电测法测模态振型

电测法测叶片振型的试验系统主要由激振系统、叶片夹持装置、信号采集系统以及数据分析系统这四部分组成，如图4所示。

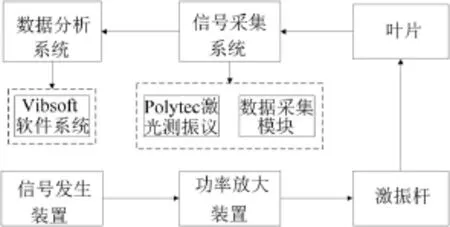
图4　电测法试验系统框图

激振系统主要包括功率放大装置、信号发生装置以及激振杆，其中，激振杆选取刚度较大的顶杆，安装在距离叶片激振点（叶片尖端中点）3 mm～5 mm距离处，如图5所示。

图5　电测法试验装置图

信号采集系统包括数据采集模块和Polytec激光测振仪，其中，Polytec激光测振仪可用来测量激振力信号和监测点的响应信号，并将振动调理器处理得到的信号送至数据采集模块。

试验时，通过激振系统对叶片施加简谐激振，激振频率接近于叶片各阶的固有频率，使叶片的振动达到共振状态，开启Polytec激光测振仪，绘制叶片网络节点，并进行逐点扫描测量叶身的稳态振动位移响应，根据多点位移响应拟合叶片在各阶共振频率下的振动位移和相位，进而绘制出叶片的振动振型，如图6所示。

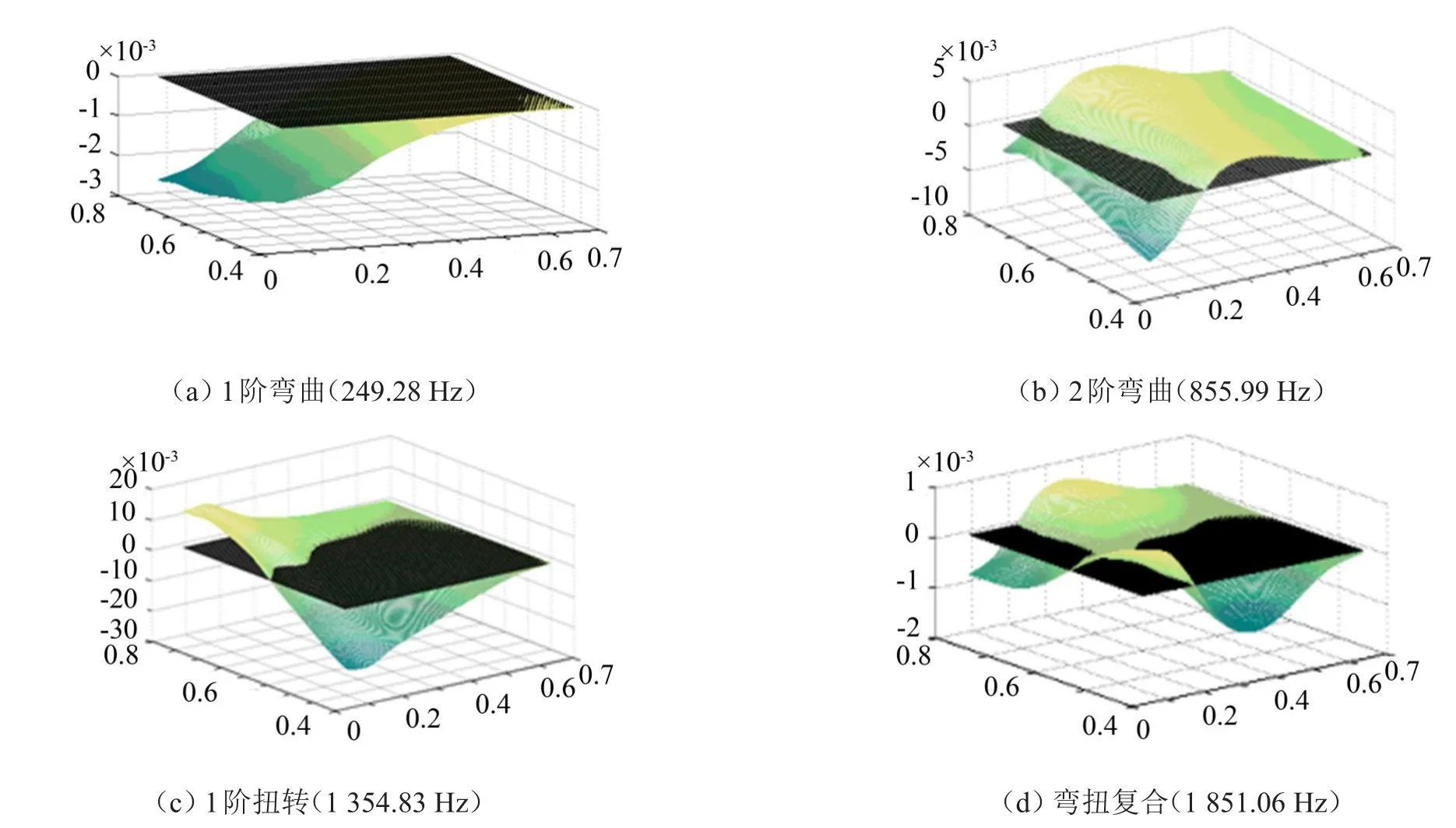
图6　叶片振型

1.3模态计算与测试结果分析

分析对比模态仿真计算结果与试验测试的结果，固有频率的平均计算误差为2.3%，最大误差为3.4%，均小于5%，在允许的计算误差范围内，如表4所示。

表4　仿真与试验结果分析对比

同时计算所得叶片振型与电测法扫描所得振型一致，则仿真分析结果与试验测试结果相吻合，说明所建叶片的有限元模型准确可靠，可以运用于接下来的叶片轮盘耦合分析中。

2　叶片轮盘耦合分析

2.1静力分析确定疲劳损伤位置

该型发动机风扇三级叶片轮盘系统为29阶循环对称结构，每一个子结构的特征性质均相同，建立一个子结构的模型并对其进行循环扩展即可得到如图7所示的完整叶片轮盘模型，其中，叶片与轮盘之间通过承力销钉连接，并将叶片耳环内侧及销钉表面设置为面面接触。

图7　叶片轮盘系统模型

已知该型发动机转速范围为3 500 r/min至11 320 r/min，考虑到转速大小可能会对应力分布规律产生影响，在计算时，将边界条件设置为叶片轮盘系统分别具有3 500 r/min、4 500 r/min、5 500 r/min、6 500 r/min、7 500 r/min、8 500 r/min、9 500 r/min、10 500 r/min及11 320 r/min的离心转速载荷，且对轮盘内圈所有节点施加位移的完全约束ALL DOF，进行非线性静力分析，观察叶片应力最大位置、应力分布方式及应力分布有无变化规律。结果显示叶片轮盘系统在不同离心转速载荷下应力分布方式相近，无明显变化规律，且叶片的应力最大位置均为与叶高方向垂直的耳环处，及耳环与橼板的转接处，如图8所示。

图8　叶片轮盘系统静力分析结果

更改叶片、轮盘子结构的单元格尺寸，将二者均设置为1 mm，分别重新划分网格并进行装配耦合，共得到101 687个单元，进行循环扩展后设置相同的边界条件进行计算，计算结果与图8中结果相一致，说明计算精度足够，前后两次设置的单元节点数量均满足要求。

综合上述静力分析并参考如图9所示的外场失效叶片，可以确定该型发动机风扇叶片易产生疲劳损伤的位置主要有两处，一是与叶高方向垂直的两耳环处，二是两耳环与橼板的转接部位。

图9　失效叶片

2.2振动分析确定共振状态

发动机的危险共振情况通常通过坎贝尔图［6］来确定，对于叶片轮盘系统而言，发生共振时须同时满足两个条件［7］：

（1）叶盘系统振动的节径数等于激振力的阶次；

（2）坎贝尔图中的叶盘系统频率曲线与激振力频率曲线存在交点。

由于该型叶片轮盘共29个叶片，且前一级的静子数为44，所以当激振力阶次K选取44时［8］，节径数不可能达到44，即该叶片轮盘系统不可能出现高频激振力引起的共振，则只考虑低频激振力引起的共振情况，即选取K为1～4。同时叶片在与轮盘系统一起转动时承受着沿叶片展向的离心载荷的影响，叶片的弯曲刚度因此而增加，使得转动状态下的叶片频率与静止状态下的固有频率不一致，即叶片在转动状态下的各阶频率是随系统转速的改变而发生变化的，则将叶片轮盘系统静力分析的结果作为预应力，其他边界条件保持不变，进行模态分析，提取叶盘系统在不同转速下的共振频率，如表5所示。

表5　叶片轮盘系统动态频率

利用表5中数据依次画出叶片轮盘系统的动频曲线，结果显示叶片轮盘系统的各阶动频曲线均满足线性规律，且频率随系统转速的升高而单调递增，其如图10所示。

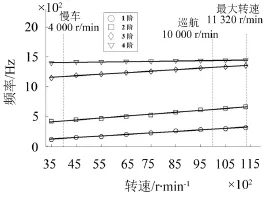
图10　动频曲线

激振力频率曲线为过坐标原点的、斜率为K/60的射线，结合动频曲线图画出个共振图，发现2阶动频曲线与4阶次激振力频率曲线存在交点，如图11所示。

图11　坎贝尔图

根据图11结果可知，该型叶片轮盘系统的危险共振转速为8 425.51 r/min。参照之前叶片轮盘系统静力分析的方式，对循环扩展后的完整叶盘模型的轮盘内圈节点施加位移的完全约束，对系统整体施加大小为8 425.51 r/min的离心转速载荷，进行静力计算，并将计算结果作为预应力，进行模态分析计算，查看叶片轮盘系统在危险共振转速下的4节径2阶模态振型，结果如图12所示。

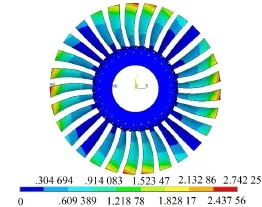
图12　叶片轮盘系统的危险共振振型

图12中结果显示，叶片轮盘系统在危险共振转速下的4节径2阶频率为567.29 Hz，与共振图中拟合出的交点频率相近，其振动形式为1阶弯曲振动。

综合上述振动分析，可以确定该型叶片轮盘系统的危险共振转速为8 425.51 r/min，危险共振频率为567.29 Hz，危险共振形式为一阶弯曲振动。

3　结语

本文针对该型发动机风扇叶片进行了模态的仿真分析计算，得到了叶片的固有频率和振型，并通过模态试验测试验证了仿真计算的正确性及所建叶片模型的合理性。在此基础上建立了叶片轮盘系统，进行了静力分析和振动分析，确定了叶片易出现疲劳损伤的位置以及叶片轮盘系统的共振状态，具体研究结论如下：

（1）该型叶片轮盘系统在不同离心转速载荷下等效应力分布方式相近，无明显变化规律，且应力集中部位，即叶片易出现疲劳损伤的位置，主要有两处，一是与叶高方向垂直的两耳环处，二是两耳环与橼板的转接部位，可针对这两个位置采取诸如喷丸、激光冲击等强化处理措施延长叶片使用寿命。

（2）该型叶片轮盘系统不可能出现高频激振力引起的共振，可能会发生低频激振力引起的共振情况，共振形式为一阶弯曲振动，共振频率为567.29 Hz，产生危险共振的转速为8 425.51 r/min，则为延长该型叶片的使用寿命，发动机在工作时应尽量避免在这一转速下长时间运转。

［1］YAN XIAOJUN，NIE JINGXU.Creep-fatigue tests on full scale directionally solidified turbine blades［J］.Journal of Engineering for Gas Turbines and Power，2008，130（4）: 044501.1-044501.5.

［2］闫晓军，孙瑞杰，邓瑛，等.涡轮叶片复合疲劳特性曲线及其规律的试验［J］.航空动力学报，2011，26（8）：1824-1829.

［3］唐铃，尚柏林，陈鹏飞，等.某型发动机风扇叶片高低周复合疲劳特性的研究［J］.机械强度，2016，38（2）：374-379.

［4］李其汉，胡壁刚，徐志怀.航空发动机强度振动测试技术［M］.北京：北京航空航天大学出版社，1995：137-138.

［5］周鋐，曹阳光，刘浩，等.汽车顶棚约束模态与工作模态分析与比较［J］.噪声与振动控制，2016，36（2）：84-87.

［6］吕文林.航空发动机强度计算［M］.北京：国防工业出版社，1988：82-85.

［7］闫晓军，聂景旭.涡轮叶片疲劳［M］.北京：科学出版社，2013：140-141.

［8］李其汉，王延荣.航空发动机结构强度设计问题［M］.上海：上海交通大学出版社，2014：63-65.

Damage Prediction and VibrationAnalysis of the Fan Blades of an Engine

TANGLing，SHANG Bo-lin，GAO Xing-wei，CHENG Peng-fei，YIN Zhi-peng
（College ofAeronautics andAstronautics，Air Force Engineering University，Xi’an 710038，China）

The method to prolong the service lifespan of the fan blades for a certain engine is studied.The measurement points and locations of fatigue damage and the resonance state monitoring are predicted，and the relevant measures are proposed.The blade model is established through Ansys，and the accuracy is verified by modal analysis and test.On this basis，model of the wheel and blade system is established.The location of fatigue damage is determined by static analysis of the system，and the resonance rotating speed，frequency and type are acquired by modal analysis of the prestressed system.The results show that the distributions of equivalent stress of the system are similar one another under different rotating speed loads.The blade has two critical locations for the fatigue damage，one is on the lug and the other is on the rafter.All the dynamic frequency of the blade-wheel system increases linearly with the increase of the rotating speed. High frequency exciting force cannot lead to resonance for this system，but low frequency exciting force can.And the resonance type is the first order bending vibration，the resonance rotating speed is 8 425.51 r/min，the resonance frequency is 567.29 Hz.

vibration and wave；modal analysis；risk assessment part；fan blade；damage predicticn

V231.92；V232文献标示码：ADOI编码：10.3969/j.issn.1006-1335.2016.05.034

1006-1355（2016）05-0164-05

2016-05-31

唐铃，（1992-）男，四川省广安市人，硕士研究生，研究方向为航空发动机振动测试与故障诊断，航空发动机结构强度。E-mail:tal1120100593@qq.com