基于机匣振动信号的滚动轴承故障特征提取

韩　特，蒋东翔，付道鹏

（电力系统及发电设备控制与仿真国家重点实验室，清华大学 热能工程系，北京 100084）

基于机匣振动信号的滚动轴承故障特征提取

韩特，蒋东翔，付道鹏

（电力系统及发电设备控制与仿真国家重点实验室，清华大学 热能工程系，北京 100084）

通过进行带机匣测点的滚动轴承故障模拟实验，获取滚动轴承在故障状态条件下，轴承座测点和机匣测点的振动数据。分析结果显示，相对于轴承座，机匣上的振动信号成分复杂，轴承故障特征不明显，直接进行包络解调无法提取故障特征。通过奇异值分解（singular value decomposition，SVD），差分谱中各峰值处奇异值可以表征不同成分的信号。当轴承故障信号微弱时，第一个峰值处的奇异值重构信号往往代表转频及其调制信号分量，选取该靠后峰值处的奇异值进行信号重构可以有效提取轴承故障特征信号。研究内容为实际基于机匣测点信号的航空发动机滚动轴承故障特征提取提供了一种新的方法。

振动与波；滚动轴承；机匣测点；故障特征提取；奇异值分解；差分谱

滚动轴承发生故障时，由故障引起的脉冲冲击信号往往激发系统的高频固有振动，振动信号往往表现出频率调制的特点［1］。传统的共振解调技术是处理滚动轴承故障的一种极为有效的分析方法。通过找出共振频带进行滤波，对滤波信号进行包络解调得到低频的故障特征频率。但滤波过程中的共振频带如何选择往往依靠工程经验［2-3］。小波变换，小波包分解等方法可以对信号进行分解降噪，从而提取包含轴承故障信息分量。但依然存在小波基选取、阈值设定等问题。经验模式分解（empirical mode decomposition，EMD）通过将信号分解为一些基本模式分量（IMF）之和，再从各基本模式分量中提取故障特征。当信号中含有大量噪声时，诊断效果往往并不理想。需要对各阶基本模式分量进行降噪处理［4-6］。

滚动轴承作为支承航空发动机转子系统的重要组成部件，工作环境极其恶劣，转速高、工作环境温度高，受应力情况复杂。恶劣工作环境易引发滚动轴承故障。目前，滚动轴承故障诊断采用的振动信号多从轴承座处测得。但航空发动机内部无法安装传感器，仅通过机匣处有限的传感器进行测量［7］。由于航空发动机内部结构复杂，故障产生的激励在传递的过程中产生衰减。同时航空发动机内部、外部工作环境恶劣。变工况情况下，容易出现热应力不均匀、压气机出现喘振等现象，机匣振动信号往往反映出转频一倍频幅值大的特征。轴承故障信号容易受到其它振动信号的干扰。所以选取合适的信号处理方法进行轴承故障特征提取有重要意义。奇异值分解（Singular value decomposition，SVD）作为一种非线性滤波方法，通过将包含信号特征的Hankel矩阵分解到一系列由奇异值表征的信号子空间中。通过去除较小奇异值对应的重构信号分量达到降噪处理的目的［8-10］。

本文进一步研究了当信号中除噪声外，还含有由转频调制产生的信号分量时，奇异值分解方法能否从中准确分离轴承故障信息。利用带机匣测点的滚动轴承故障模拟实验台进行了故障模拟实验与特征信号提取，得出了一种基于差分谱的奇异值选择方法［11-14］。对所选取的奇异值进行信号重构，包络分析从而准确提取轴承故障特征。为基于机匣振动信号的航空发动机滚动轴承故障特征提取提供了参考［15］。

1　奇异值分解降噪原理

奇异值分解（SVD）定义如下：对于一个m×n的矩阵A（假定m＞n），存在一个m×m正交矩阵U和一个n×n正交矩阵V，使得

图1　机匣测点振动仿真信号分析

根据奇异值分解理论可知，各奇异值反应噪声和能量的集中情况，前几个较大的奇异值主要反映信号，排位靠后的奇异值反映噪声。选择合适奇异值进行信号重构，达到提取目标信号的目的。

2　奇异值差分谱

目前，在奇异值选择问题上主要依据寻找差分谱上的峰值位置。所谓奇异值差分谱即为以下序列

该序列反映了相邻奇异值之间的变化趋势。各奇异值由大到小排列，当差分谱上出现波峰时，说明两奇异值表征的信号分量存在较大的差异性。本质原因为信号分量之间能量不同。所以，根据差分谱中的波峰确定合适的奇异值，重构原始信号，从而得到滤波降噪和特征增强的目的。

在航空发动机滚动轴承故障特征提取中，发动机内部结构复杂，传递过程和运行工况也比较复杂。当滚动轴承出现故障时，机匣测点的振动信号不仅仅包含轴承故障频率调制产生的高频振动信号，还包含由转频调制产生的一系列振动信号和噪声信号。当轴承故障信号较微弱时，容易淹没在其他分量信号之中。通过差分谱选择合适的奇异值进行信号重构十分关键。

3　仿真信号分析

为验证方法的有效性，并说明奇异值的选择的一般性方法。数值仿真滚动轴承发生故障时，航空发动机机匣测点的振动信号x（t），主要成分有轴承故障脉冲冲击激发的高频振动信号、由航空发动机转轴振动引起的调制信号和噪声信号。数学仿真公式如下

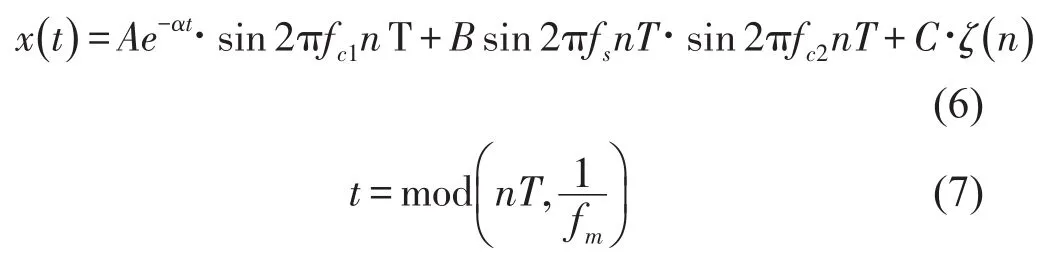
上式中α表示指数系数，T为采样间隔，n为采样点数，fm、fc1分别表示调制频率和载波频率，即轴承的故障特征频率和系统高频振动频率，fs、fc2分别为轴的转动频率和转动信号的载波频率，ζ（n）为高斯白噪声。取指数系数 α=800，采样频率f=16 000Hz，转动频率 fs=40Hz，轴承故障特征频率载波频率fc1=4 000Hz，fc2=2 000Hz。A=1，B=1，C=1.4。

轴承故障仿真信号时域波形见图1（a），机匣测点振动仿真信号时域波形见图1（b）。

加入噪声和转频信号后，频率调制现象明显减弱。对其做Hilbert包络解调变换，包络谱如图1（c），从中提取不出任何故障特征频率。

选取延迟步数k=1，m=20 000，n=30，构造Hankel矩阵，对信号x（t）做SVD分解，图2（a）给出了各阶奇异值的分布情况。根据式5计算得到奇异值差分谱见图2（b）。从差分谱中可以看到出现了两个波峰，分布在i=1、3时，根据差分谱理论，2个峰值表明信号中含有两个相关性较差的信号分量。当i≥5，各阶奇异值变化趋于平缓，差分谱上没有出现波峰，该部分奇异值可近似看作代表噪声信号分量。

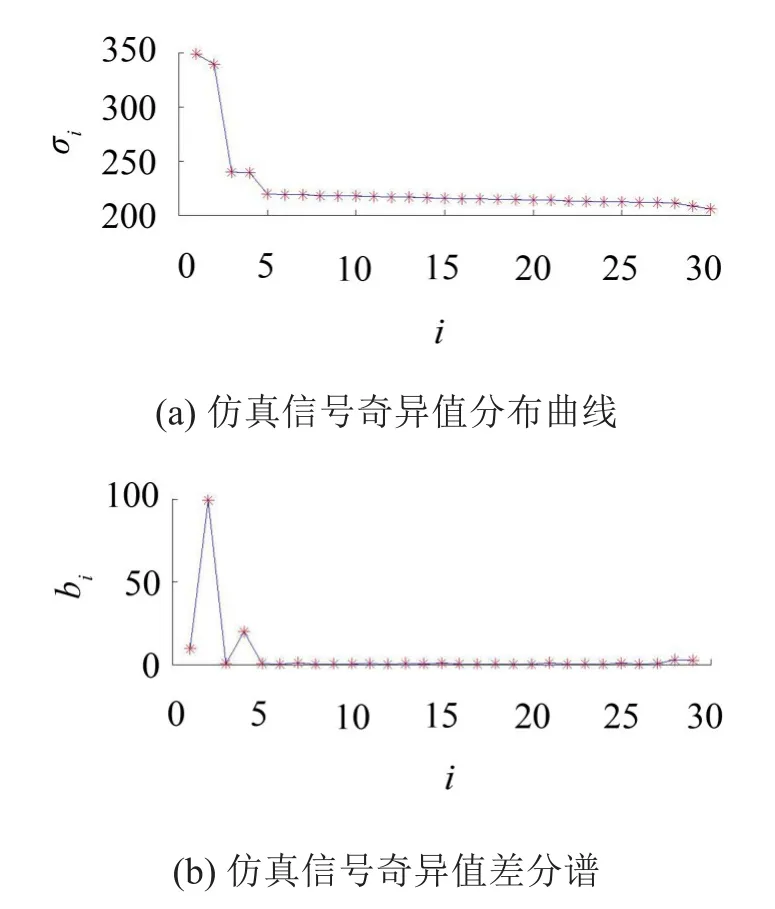
图2　机匣测点振动仿真信号奇异值分布、差分谱

从以上分析可以看出，差分谱上出现峰值的位置标明该点与该点之后的奇异值重构信号相关性差。根据差分谱的峰值位置对选择相应奇异值进行信号重构，可以将不同成分的分量信号进行有效分离，SVD分解具有良好的自适应分解能力。由于奇异值阶次反映了分量信号的能量高低，所以当故障分量信号能量较弱时，对应故障分量信号的奇异值阶次往往靠后。在差分谱上选择第一个波峰后的奇异值进行信号重构有利于提取轴承故障信号。

4　带机匣测点滚动轴承故障模拟实验

带机匣测点的滚动轴承故障模拟实验台如图5所示。主轴一端通过联轴器与电机相连，另一端通过键与弹性挡圈与风扇固定。中间为轴承座，主轴与滚动轴承内圈为过盈配合。滚动轴承外圈与轴承座为过盈配合。考虑实际航空发动机轴承座与机匣连接方式主要为螺栓连接。本实验通过四根杆单元和螺栓将轴承座与机匣固定。

图3　前3阶奇异值重构分量信号1、2、3、4

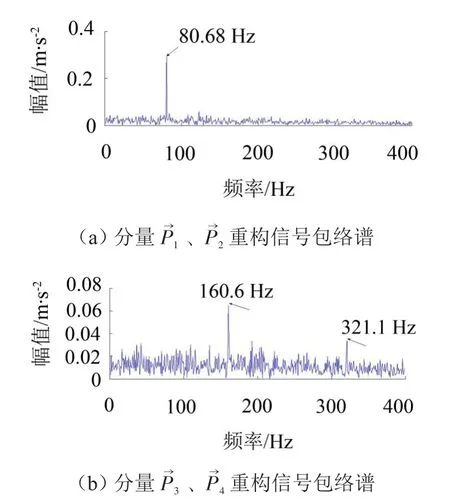
图4　

本文进行了外圈故障轴承状态下的振动实验。振动信号通过加速度传感器测量。为模拟实际航空发动机传感器多安装在机匣处，从机匣提取振动信号。除轴承座X、轴承座Y测点，本实验台在机匣上设置机匣X、机匣Y测点。通过变频器调节电机转速至实验转速1 600 r/min，由数据采集卡采集加速度传感器的振动信号，采样频率为16 000 Hz。

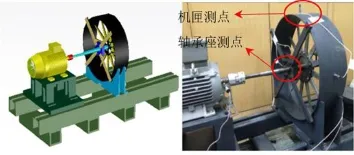
图5　带机匣测点滚动轴承故障模拟实验台

滚动轴承故障模拟实验的滚动轴承型号选用N206E圆柱滚子轴承来模拟航空发动机滚动轴承。轴承具体参数如下：内径：30 mm，外径：62 mm，轴承节径：46 mm，滚动体个数：14，滚动体直径：7.6 mm，接触角：0度。故障轴承加工方法为线切割。外圈故障裂纹宽度、深度分别为1 mm、0.5 mm。

5　基于机匣测点的滚动轴承故障特征提取

故障轴承轴承座测点振动信号时域波形和包络谱如图6（a）、图6（b）所示，机匣测点振动信号时域波形和包络谱如图6（c）、图6（d）所示。实验转速1 600 r/min，根据轴承各参数可以计算故障特征频率。外圈故障特征频率公式如式（8）。

fs为轴的转动频率，Z是轴承滚动体个数，d，D分别为滚动体直径和轴承节径，α为接触角。从而可以计算得出 fo=155.8Hz。轴承座测点的时域波形图脉冲冲击特征明显，包络谱中可以清楚看出转频27.2 Hz，外圈故障特征频率一倍频、二倍频，和三倍频成分，故障特征十分明显。机匣测点振动信号时域波形振幅相对于轴承座测点有所降低，脉冲冲击特征和频率调制特征减弱。包络谱中也无法提取任何故障特征。但可以看出明显的转动频率，说明机匣的振动信号是以转频信号及由转频调制产生的高频信号为主。轴承故障激励信号在传递过程中产生较大的衰减。机匣振动包络谱中无法提取任何故障特征频率表明轴承故障激励信号在很大程度上被湮没。本实验很好地模拟了实际航空发动机机匣测点的振动信号。

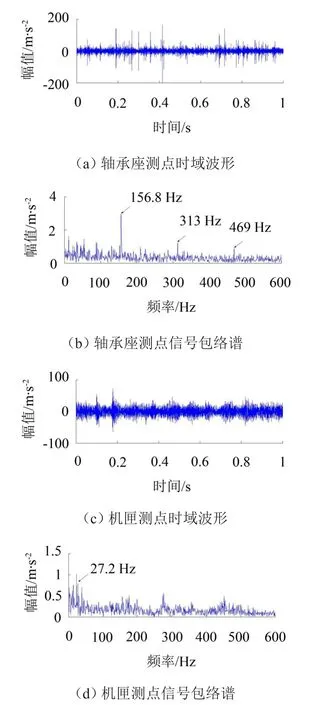
图6　

对机匣测点振动信号进行SVD分解变换，对选取延迟步数k=1，m=20 000，n=20，构造Hankel矩阵，SVD分解后所得奇异值差分谱如图7。

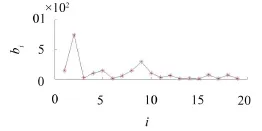
图7　机匣测点信号奇异值差分谱

从差分谱中可以看出峰值出现在i=2处，在i=5，9处也各有一个峰值。结合仿真分析中所得结论，进一步探讨各峰值处奇异值的选择原则。取第2、5、9阶奇异值进行信号重构，得到分量信号时域波形和包络谱见图8（a）至图8（f）。对于分量信号P→2只能在包络谱中提取转频的一倍频、二倍频和十倍频，各频率均与转频有关。作为奇异值差分谱上出现的第一个峰值，可以看出转频及其调制频率信号是机匣测点的振动信号的主要信号分量。从而对轴承故障信号造成干扰湮没，所以直接对机匣测定振动进行包络解调无法得到满意效果。对于分量信号，包络谱中出现转频和一些频率较高的成分，仍无法提取任何轴承故障特征频率。而在分量信号的包络谱中可以准确提取转频27.17 Hz，轴承故障特征频率的一倍频156.7 Hz、二倍频311.7 Hz和三倍频467.6 Hz。

图8　

通过以上分析可以得出，相对于轴承座测点，故障轴承的振动激励信号在传递到机匣的过程中有所衰减。机匣上存在的转频及由其调制产生的振动信号具有很大的能量。通过进行SVD分解，差分谱上第一个峰值处的奇异值往往对应与转频相关的信号分量。应忽略该处奇异值，选取在靠后谱峰处的奇异值进行信号重构，可以较为准确地反应轴承故障信号。

6　结语

首先对奇异值分解降噪理论和差分谱进行了研究，然后仿真分析了航空发动机机匣测点振动信号，最后通过进行基于机匣测点的滚动轴承故障模拟实验，获取实验数据进行故障特征提取。本文可得到以下结论：

（1）通过奇异值分解（SVD），再根据各阶奇异值重构信号，可以将信号分解为一系列分量的叠加。根据奇异值差分谱中出现峰值的位置选取合适的奇异值重构信号具有良好的自适应分解能力。

（2）基于机匣测点的滚动轴承故障模拟实验中相对于轴承座测点，对机匣测点的振动信号进行包络解调无法提取故障特征。

（3）通过对故障模拟实验数据进行特征提取发现，机匣振动信号以转频及其调制信号为主，奇异值差分谱上第一个峰值处的奇异值往往代表转频及其调制信号分量。忽略该处奇异值，选取峰值靠后的奇异值进行信号重构能有效提取滚动轴承故障信号。

［1］HO D，RANDALL R B.Optimisation of bearing diagnostic techniques using simulated and actual bearing faultsignals［J］.MechanicalSystemsandSignal Processing，2000，14（5）:763-788.

［2］王平，廖明夫.滚动轴承故障诊断的自适应共振解调技术［J］.航空动力学报，2005，20（4）：606-612.

［3］张倩.基于共振解调原理和转速阶比谱分析的滚动轴承故障诊断方法研究［D］.杭州：浙江大学，2012.

［4］艾延延，冯研研，周海仑.小波变换和EEMD-马氏距离的轴承故障诊断［J］.噪声与振动控制，2015，35（1）：235-239.

［5］夏均忠，苏涛，马宗坡，等.基于EMD的滚动轴承故障特征提取方法［J］.噪声与振动控制，2013，33（2）：123-127.

［6］刘尚坤，唐贵基.自适应MED结合EMD诊断滚动轴承早期故障［J］.噪声与振动控制，2015，35（6）：159-162.

［7］陈果，郝腾飞，程小勇，等.基于机匣测点信号的航空发动机滚动轴承故障诊断灵敏性分析［J］.航空动力学报，2014，29（12）：2875-2884.

［8］REZA GOLAFSHAN，KENAN YUCE SANLITURK. Study on hankel matrix-based SVD and its application in rolling element bearing fault diagnosis［J］.Mechanical Systems and Signal Processing，70-71（2016）:36-50.

［9］王超，孔凡让，黄伟国，等.改进的奇异值分解在轴承故障诊断中的应用［J］.振动工程学报，2014，27（2）：296-303.

［10］冷永刚，郑安总，范胜波.SVD分量包络检测方法及其在滚动轴承早期故障诊断中的研究［J］.振动工程学报，2014，27（5）：794-800.

［11］QIAO Z J，PAN Z R.SVD principle analysis and fault diagnosis for bearings based on the correlation coefficient［J］.Measurement Science and Technology，2015，26（2015）085014.

［12］XUEZHI ZHAO，BANGYAN YE.Selection of effective singularvaluesusingdifferencespectrumandits application to fault diagnosis of headstock［J］.Mechanical Systems and Signal Processing，25（2011）:1617-1631.

［13］赵学智，叶邦彦，林颖.奇异值分解对轴承振动信号中调幅特征信息的提取［J］.北京理工大学学报，2011，31（5）：572-577.

［14］张超，陈建军，徐亚兰.基于EMD分解和奇异值差分谱理论的轴承故障诊断方法［J］.振动工程学报，2011，24（5）：539-545.

［15］党相懿.机匣振动故障模拟实验和特征提取方法研究［D］.北京：清华大学，2014.

Fault Feature Extraction of Rolling Bearings Based on Casing Vibration Signals

HANTe，JIANG Dong-xiang，FU Dao-peng
（State Key Lab of Control and Simulation of Power Systems and Generation Equipment，Department of Thermal Engineering，Tsinghua University，Beijing 100084，China）

Fault feature extraction of rolling bearings based on casing vibration signal is studied.The experiment for the fault simulation of the rolling bearings is done and the vibration signals of the bearing base and casing are acquired. Analysis results show that，compared to the bearing base，the vibration signal of the casing is complex and the fault feature of the bearing is not obvious.The envelope demodulation method cannot extract the fault characteristics directly.Therefore，the singular value decomposition（SVD）is employed to process the vibration signal.It is found that the singular values at different peaks in the difference spectrum can represent the signals of different components.The singular value reconstruction signal at the first peak always represents the components of the rotating frequency and modulation signals when the fault signals of the bearing are weak.The fault modulation signals can be effectively extracted by selecting the singular values after the first peak in the difference spectrum.This study provides a new method for the fault feature extraction of rolling bearings based on the vibration signals of casing.

vibration and wave；rolling bearing；casing measurement point；fault feature extraction；singular value decomposition（SVD）；difference spectrum

TP206+.3

ADOI编码：10.3969/j.issn.1006-1335.2016.05.030

1006-1355（2016）05-0144-06

2016-01-17

国家自然科学基金资助项目（11572167）

韩特（1993-），男，合肥市人，直博研究生，主要研究方向为燃气轮机、航空发动机故障诊断与结构健康监测，信号处理与数据挖掘。

蒋东翔，男，博士生导师。E-mail:jiangdx@mail.tsinghua.edu.cn