基于复色共焦的透明材料厚度测量数据处理方法研究

安喆， 徐熙平， 乔杨， 张宁， 吕耀文

(长春理工大学 光电工程学院， 吉林 长春 130022)



基于复色共焦的透明材料厚度测量数据处理方法研究

安喆， 徐熙平， 乔杨， 张宁， 吕耀文

(长春理工大学 光电工程学院， 吉林 长春 130022)

为了解决精密光学透镜制造、玻璃容器生产等透明材料相关行业对厚度检测的需求，采用复色共焦法对透明材料厚度进行检测。介绍了共焦系统测量原理，提出了测量结构方案，构建了测量实验装置，并对实验装置进行了标定。利用线性回归法对实验数据进行处理：使用线性预测函数建模，根据实测数据确定模型中各个参数，并对误差进行补偿，完善了厚度模型。实验结果表明：共焦系统的测量范围达到15 mm，测量精度为±3 μm，从而证明该方法是一种高精度的在线非接触测量方法。

仪器仪表技术； 共焦法； 透明材料； 厚度测量； 线性回归

0　引言

透明材料厚度的测量是工业生产中的关键环节，主要可分为接触式测量法和非接触式测量法。接触式测量法的量具直接接触材料产生应力，不但影响测量精度，而且容易划伤材料表面。随着光学技术和电子技术的发展，非接触测量的精度越来越高，现已成为工业生产领域的主要测量方法[1-2]。国外多使用外差激光干涉法来测量透明材料厚度[3-5]，但由于激光偏振态的不稳定,容易引起干涉光路中两种频率的偏振光不能彻底分开，从而影响测量。国内多采用激光三角法测量透明材料的厚度[6-8]，它利用像点在传感器上的位置来确定物点的空间位置，但照射到物体表面的激光会产生散斑效应，像点在传感器上通常不是简单的一个点，从而很难确定像点的位置，误差较大。本文提出采用共焦技术测量透明材料厚度[9]，并针对如何根据样本数据，建立预测模型这一问题，选用线性回归法对数据进行处理，从而确定预测模型中的参数，最终得到测量结果。

1　共焦法测量原理

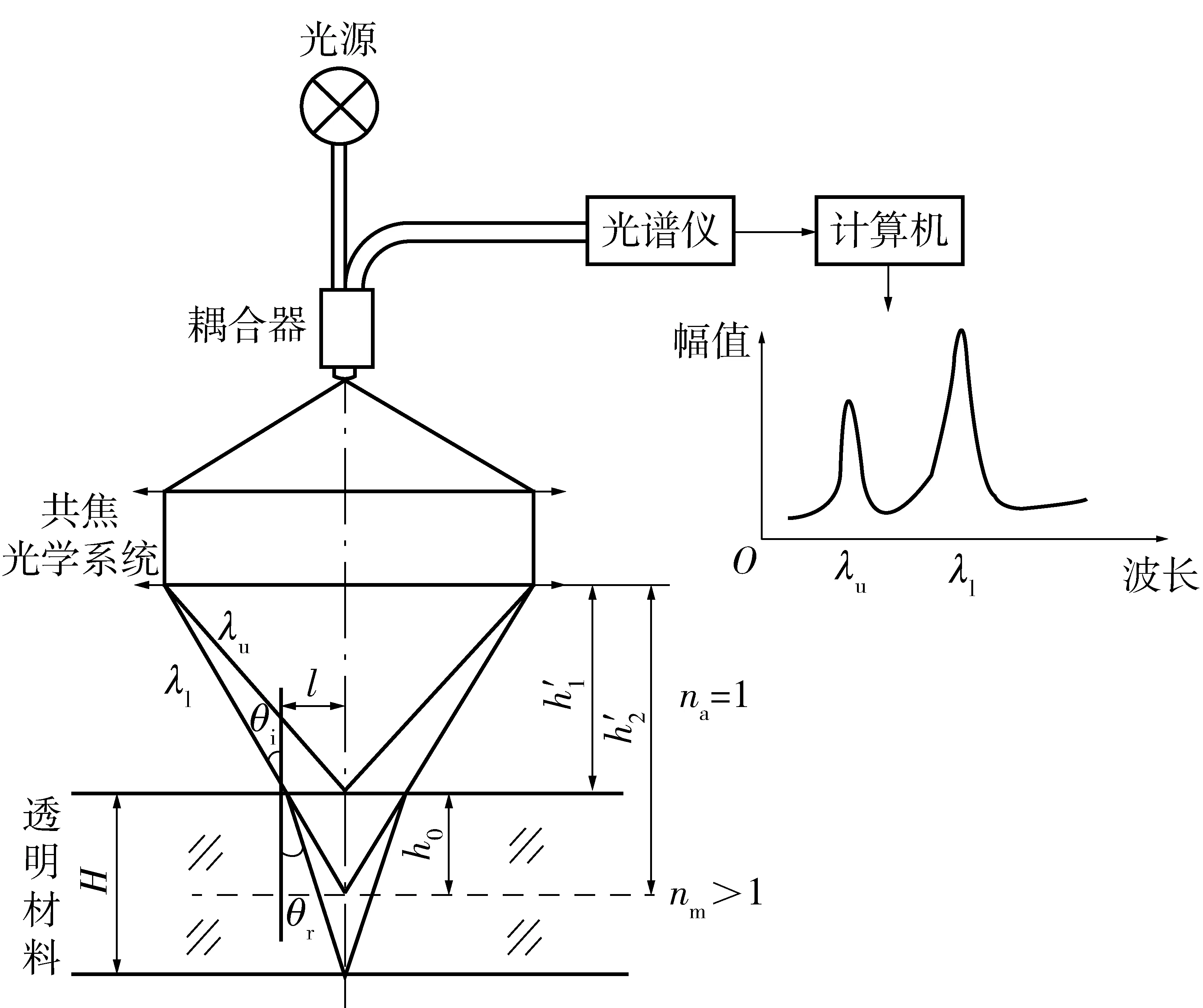
图1　共焦法测量透明材料厚度原理图Fig.1　　　　Measurement of transparent material thickness based on confocal method

共焦法的原理图如图1所示，从光源发出的复色光经过光纤及耦合器传输，经过发射光学系统后产生轴向色差，并按波长依次分布。不同波长的光会聚在光轴的不同位置，测量范围由最短波长焦点与最长波长焦点之间的距离决定，系统选用的光源光谱和分光系统适用的波长范围决定了最短波长和最长波长的大小。当某一波长的焦点与透明材料表面重合时，载有被测物质信息的光将被材料上、下表面反射并按原路返回，反射光通过光纤进入分光系统，经光谱测量和分析，由数学模型计算出对应两个波长的距离，从而得到待测透明材料的厚度。

系统经光谱测量可以得到透明材料的上、下表面反射波长，分别设为λu和λl. 即此时入射光线经过透明材料上表面发生折射，入射角为θi，折射角为θr.h0为两单色光焦点之间的距离，H为待测透明材料厚度。

由折射定律可知

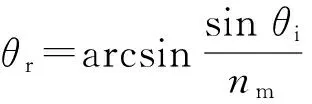
(1)

式中：na为空气折射率，na=1；nm为透明材料的折射率。

又因为

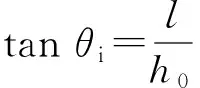
(2)

并且

(3)

由(1)式、(2)式、(3)式可得透明材料厚度为

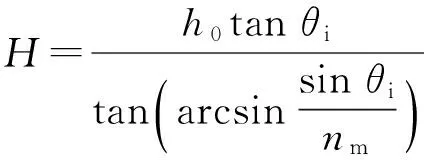
(4)

在工程实际中，透明材料的折射率不同，为了使公式具有普遍性，故将(4)式进一步简化，此时nm独立，不受任何参数影响：

(5)

2　测量装置构建与标定

2.1测量装置构建

图2　共焦测量实验装置图Fig.2　Confocal measuring experimental facility

实验装置如图2所示，由复色光源、传输光纤、共焦光学系统、待测透明材料、平移工作台、光谱仪、计算机构成。

各部分技术指标如下：

1)光源选用卤钨灯白光光源，其波长范围为360～2 200 nm.

2)光谱仪的光谱范围为360～850 nm，分辨率为0.02 nm.

3)选用的光纤纤芯直径为200 μm，可对波长在200～1 100 nm范围内的光进行传输。

4)系统选用LabVIEW图形化编程软件作为上位机软件进行仿真。

2.2平面反射镜标定

利用ZEMAX光学设计软件模拟光路，并将光学系统前端面到任意波长的光所对应焦点距离的计算值作为理论距离，用h表示。由于系统在装配、实际测量等过程中会与理论值产生偏差，因此需要对共焦光学系统进行标定。

本实验选择平面反射镜进行系统的标定，利用平面镜的反射原理，可以得到任意波长的光对应焦点的位置。标定过程如下：测量时将平面反射镜置于平移工作台上，以450 nm波长的光所对应的实际距离为基准，调整平移工作台高度h′(h′为光学系统前端面到不同波长的光所对应焦点的实际距离)，此时在LabVIEW中观察波长改变，波长每改变20 nm记录一次实际距离。

为了保证测量结果的准确性，以450～750 nm波长的光对应的距离为一组数据，进行10次重复测量，并对10组数据的波长、实际距离、理论距离分别取平均值，最后得到一组平均数据(见表1)。

从实验数据可以看出，理论距离与实际距离误差控制在±0.049 mm范围内，精度不高，且呈非线性，因此在厚度模型建立时需要对曲线进行修正。

为了建立厚度测量模型，就要找到波长与实际距离的关系公式。基于实验的物理意义以及散点图的大致趋势，选择用线性回归法进行拟合。

3　线性回归算法与厚度模型的建立

3.1线性回归算法机理

对波长和实际距离进行m次独立观测，得到样本数据集合{λk|h′k}，集合代表了实际距离h′k对于波长λk的依赖关系，利用线性回归表示h′k与λk的依赖关系为

h′k=a+bλk+ε，

(6)

式中：λk是波长在第k次观测时的取值；a、b为回归

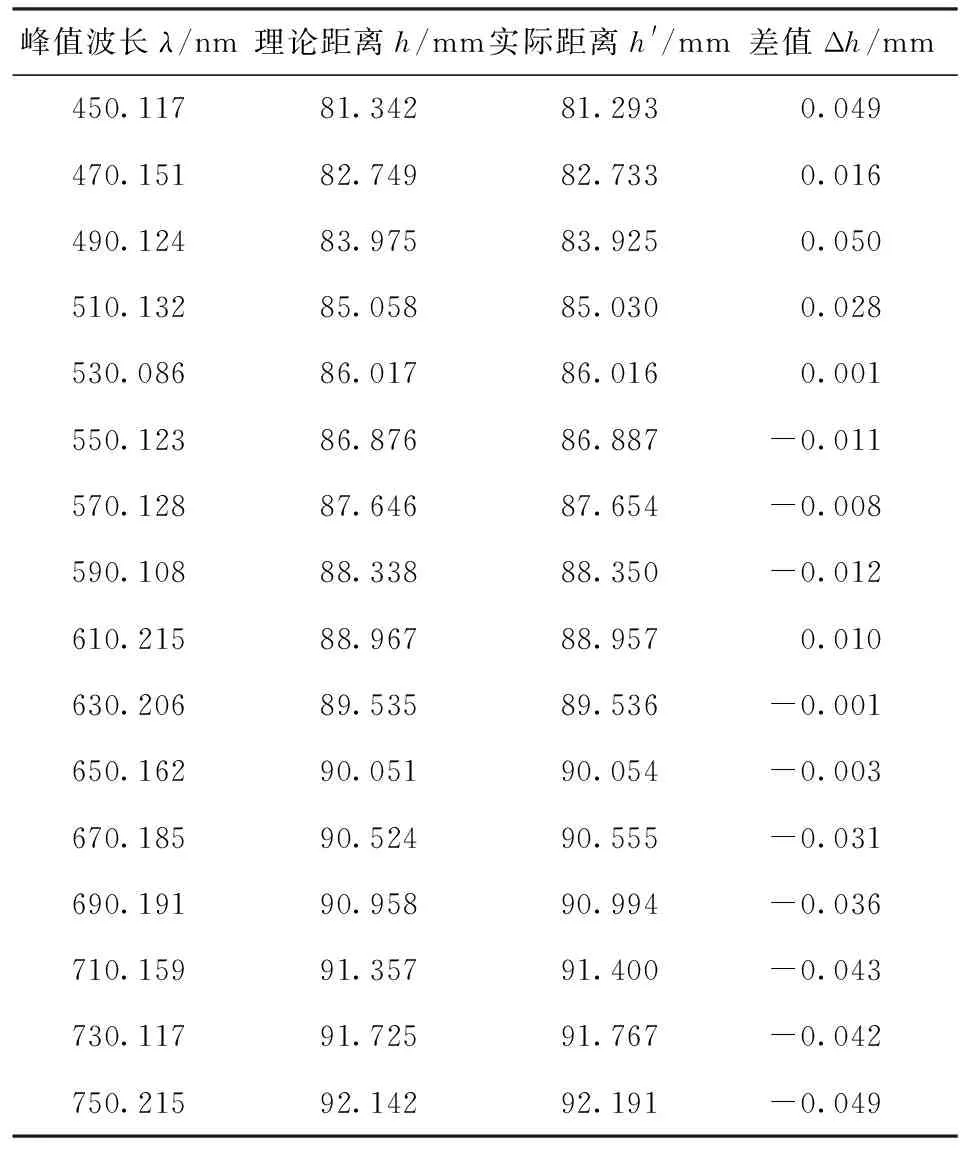
表1　测量范围精度实验数据表

系数；h′k是一个随机变量，随机性由随机误差ε造成。

线性回归的经验拟合方程可用最小二乘原理得到，其方程为

(7)

3.2厚度模型的建立

将表1数据代入方程(7)式，得到拟合直线为

h′=0.034 6λ+67.193 5.

(8)

拟合结果如图3所示。

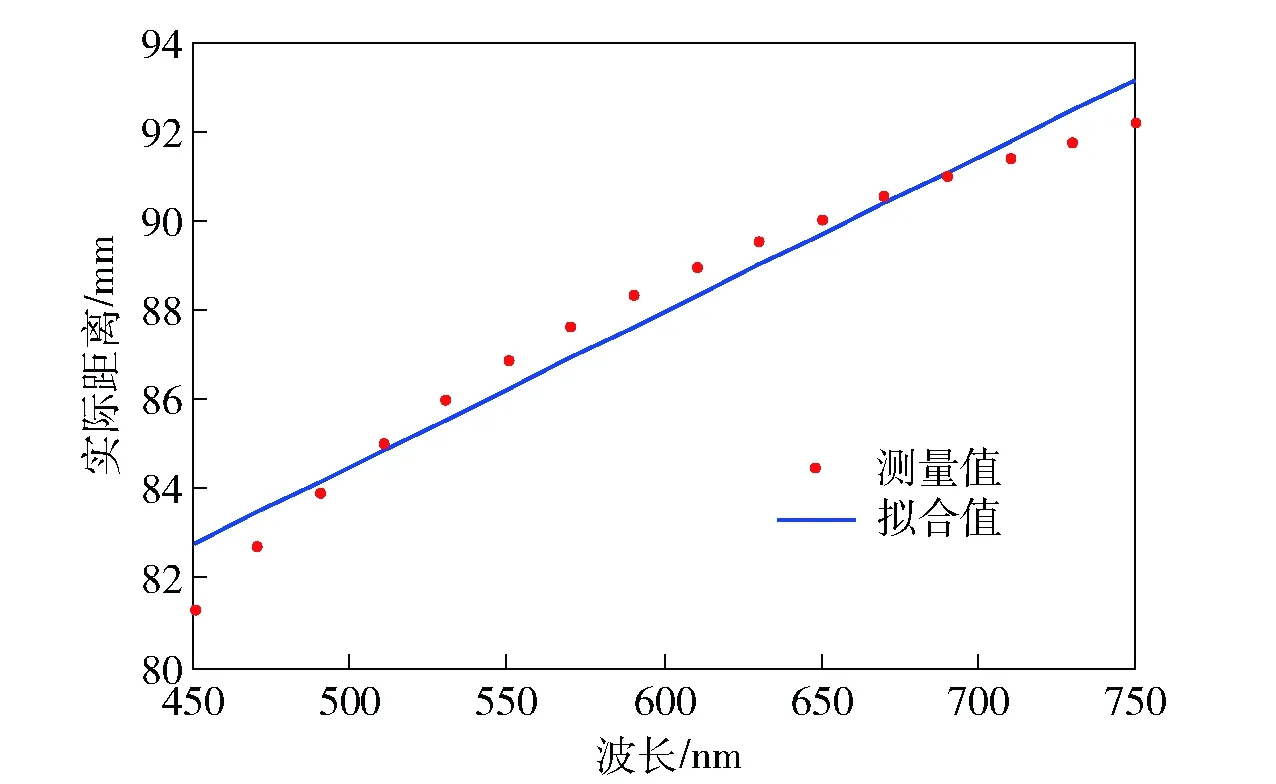
图3　波长与实际距离拟合图Fig.3　Fitting graph of wavelength and actual range

通过计算自变量与因变量之间的相关系数，以此来评定拟合的优良程度。求取相关系数的公式为

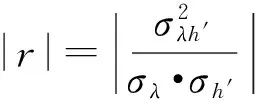
(9)

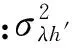
(10)

将表1数据代入(10)式得相关系数|r|=0.979 3，相关系数在满足0.7≤|r|<1时为高度线性相关。这代表两变量间线性相关非常密切，所有数据出自同一个信号源的可能性很高。

线性回归拟合的直线与原始数据存在一定的误差，根据方差公式求得：S2=6.950 7. 由于方差越接近于0，误差越小。因此为了减小随机误差ε，需要对拟合直线进行补偿。根据数据情况将其进行分段线性拟合。补偿结果如图4所示。

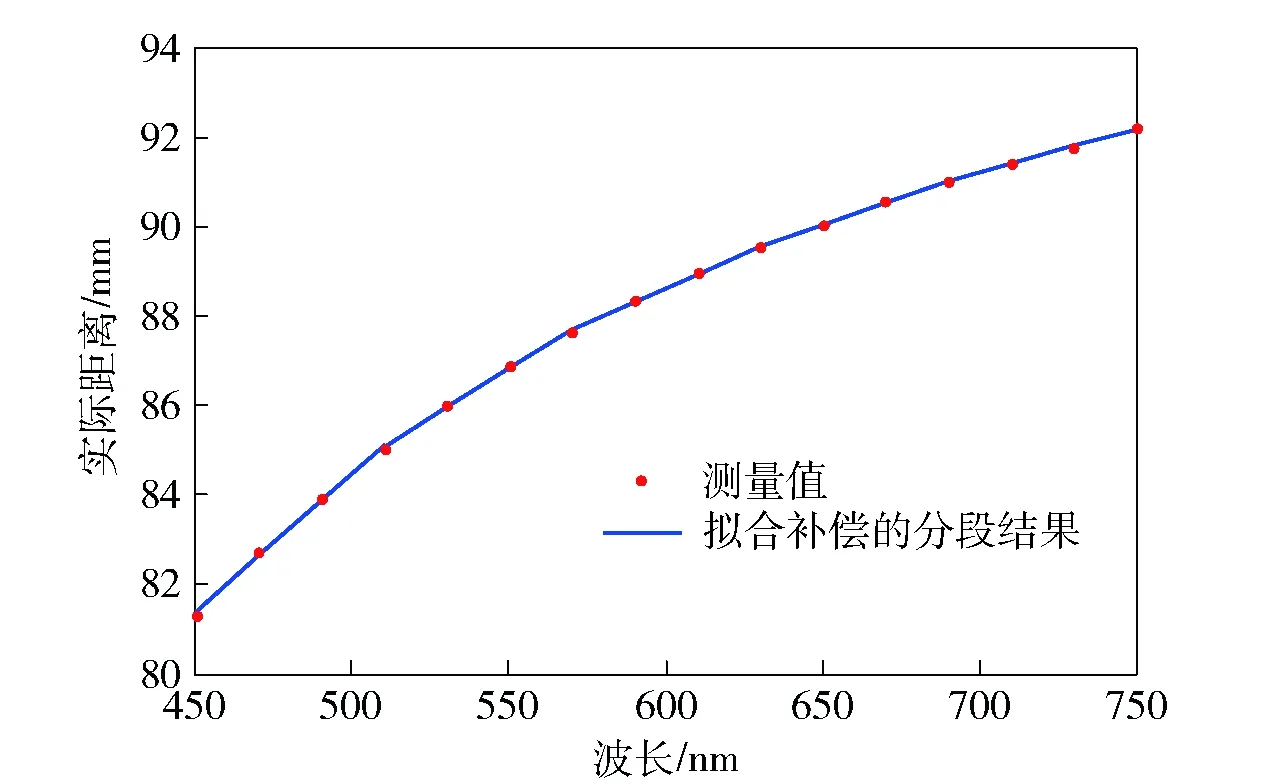
图4　补偿后波长与实际距离关系曲线Fig.4　　　　The relationship between wavelength and actual range after compensation

补偿后的分段函数为

(11)

分别对补偿后的每段直线求方差，结果如表2所示。

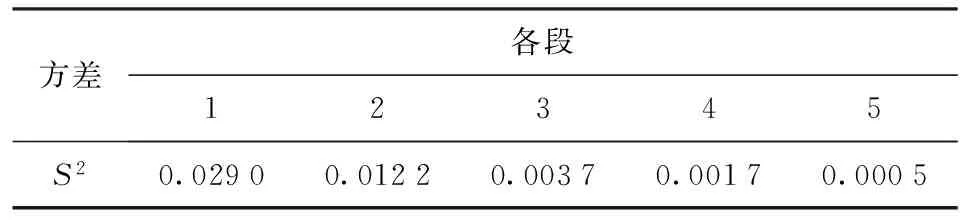
表2　补偿后各段方差数据表

测量透明材料时，将上表面反射的峰值波长λu代入(11)式中可得光学系统前端面到λu焦点的距离，并将其记为h′1；同样将透明材料下表面反射的峰值波长λl代入(11)式中得到h′2. 由图1可知：h0=h′2-h′1.

对于图1中θi，可用上述同样的数据处理方法得到不同波长的光与其对应θi之间的关系。

此外，透明材料的折射率随波长的改变而不同，以石英玻璃为例，不同波长的光所对应的折射率如表3所示。

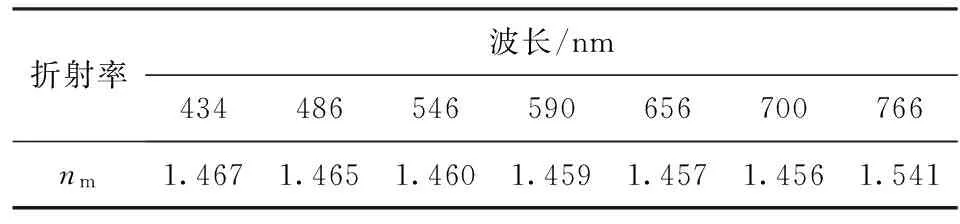
表3　石英玻璃波长和折射率表

用Matlab对表3数据进行拟合，得到石英玻璃折射率与波长关系公式为

nm=0.000 135 7λ+1.391.

(12)

其他材料的折射率可用相同方法得出。

综上所述，共焦系统测量透明材料厚度公式为

(13)

实验选用厚度标定值分别为2.964 mm、7.937 mm、9.894 mm、14.926 mm的石英玻璃进行5次重复测量，测量结果如表4所示。

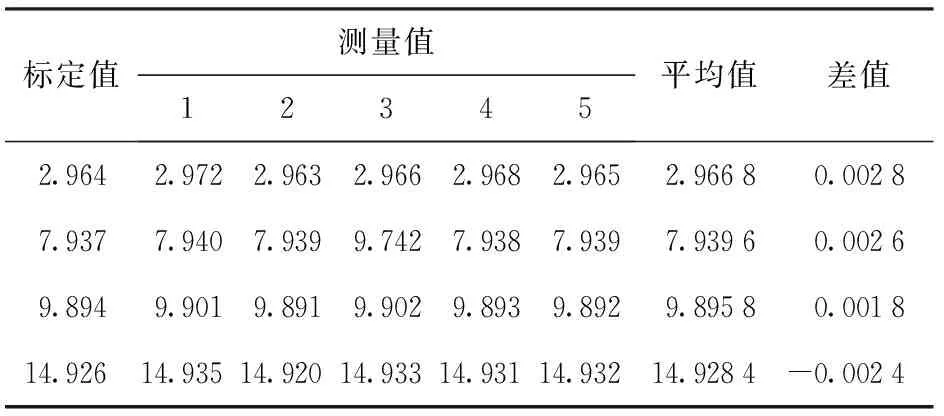
表4　石英玻璃厚度测量数据表

由表4的实验数据可见，平均测量误差为±3 μm，实验结果满足测量要求。

4　结论

本文采用共焦法非接触测量检测透明材料厚度，对波长为450～750 nm的光对应的实际距离进行重复测量，利用线性回归法对实验数据进行拟合，通过计算拟合方程的相关系数来评定拟合的优良程度，并对拟合误差进行补偿，从而建立厚度测量模型。系统平均测量精度为±3 μm，测量范围为15 mm. 如果在宽光谱内进行测量，测量范围将更高。实验结果表明，共焦系统能够对透明材料进行高精度测量，可应用于光学零件加工、平板玻璃的生产过程中。

References)

[1]罗胜彬, 宋春华, 韦兴平, 等. 非接触测量技术发展研究综述[J]. 机床与液压,2013, 41(23):150-153.

LUO Sheng-bin, SONG Chun-hua, WEI Xing-ping, et al. Review for the development and research of non-contact measurement technology[J]. Machine Tool and Hydraulics, 2013, 41(23):150-153. (in Chinese)

[2]陈文刚,丁建军. 几种测厚仪器的研究与应用[J]. 工业技术创新,2015，2(3):380-384.

CHEN Wen-gang, DING Jian-jun. Research and application of some thickness gauges[J].Industrial Technology Innovation, 2015，2(3):380-384. (in Chinese)

[3]Shukla R P,Udupa D V,Das N C, et al. Non-destructive thickness measurement of dichromated gelatin films deposited on glass plates[J]. Optics and Laser Technology, 2006, 38(3):552-557.

[4]Maruyama H, Inous S, Mitsuyama T, et al. Low-coherence interferometer system for the simultaneous measurement of refractive index and thickness[J]. Applied Optics, 2002, 41(3): 1315-1322.

[5]Bing H, Cabestaing F. Narrow-band frequency analysis for laser-based glass thickness measurement[J]. Transactions on Instrumentation and Measurement, 2005, 54(1):222-227.

[6]孙晶玢. 基于差分激光三角法的水面油膜测厚系统光学传感器设计[D]. 天津：天津大学, 2010.

SUN Jing-bin. Research and development of optical sensor for oil film thickness measurement on the water surface based on differential laser trigonometry[D].Tianjin: Tianjin University, 2010. (in Chinese)

[7]王晓嘉，高隽，王磊．激光三角法综述[J]．仪器仪表学报，2004,25(4): 601-604.

WANG Xiao-jia, GAO Jun, WANG Lei. Overview of laser triangulation[J]. Chinese Journal of Scientific Instrument， 2004,25(4):601-604. (in Chinese)

[8]杨桂栓,陈涛,张志峰. 基于激光三角法对透明平板厚度测量光线补偿的研究及应用[J]. 中国激光,2015,42(7):219-226.

YANG Gui-shuan, CHEN Tao, ZHANG Zhi-feng.Study and application on transparent plate thickness measurement based on laser triangulation with light compensation[J]. Chinese Journal of Lasers,2015,42(7):219-226. (in Chinese)

[9]乔杨,张宁,徐熙平,等. 基于共焦法的透镜厚度测量系统设计[J]. 仪器仪表学报,2011,32(7):1635-1641.

QIAO Yang, ZHANG Ning, XU Xi-ping, et al. Design of lens thickness measurement system based on confocal technology[J]. Chinese Journal of Scientific Instrument, 2011,32(7):1635-1641. (in Chinese)

Research on Approaches to Processing of Measured Thickness Data of Transparent Material Based on Polychromatic Confocal Technology

AN Zhe, XU Xi-ping, QIAO Yang, ZHANG Ning, LYU Yao-wen

(School of Electro-Optic Engineering，Changchun University of Science and Technology，Changchun 130022，Jilin，China)

In order to meet the requirement of measuring thickness of transparent materials for precision optical lens and glass container, etc., the polychromatic confocal method is used to measure the thickness of transparent material. The measuring principle of confocal system is introduced. A measuring structure scheme is proposed, and an experimental device is constructed and calibrated. The linear regression method is adopted to process the experimental data. The proposed method is to use linear prediction function to construct a mathematical model. The parameters in the model are determined using the measured data. The thickness model is improved by compensating error. The experimental results show that the measuring range of confocal system can reach 15 mm, and the accuracy of measurement is ±3 μm. The compound color confocal method is a kind of online non-contact measurement technique with high precision.

apparatus and instruments technology; confocal technology； transparent material； thickness measurement； linear regression

2015-11-12

吉林省科技发展计划项目(20120357)

安喆(1992—)，女，博士研究生。E-mail: 2955100200@qq.com；

徐熙平(1969—)，男，教授，博士生导师。E-mail: xxp@cust.edu.cn

TH741

A

1000-1093(2016)10-1964-05

10.3969/j.issn.1000-1093.2016.10.025