改进的遗传算法求解火力分配优化问题

董朝阳,路遥,王青

(1.北京航空航天大学航空科学与工程学院,北京100191;2.北京航空航天大学自动化科学与电气工程学院,北京100191)

改进的遗传算法求解火力分配优化问题

董朝阳1,路遥1,王青2

(1.北京航空航天大学航空科学与工程学院,北京100191;2.北京航空航天大学自动化科学与电气工程学院,北京100191)

提出一种求解火力分配优化问题的改进遗传算法。基于目标函数的相对大小构造适应度函数,较传统的界限构造法更加显著地体现染色体之间的差异,使得优良染色体更容易被选中,从而提高算法的收敛精度。采用基于父代染色体相似度的启发式遗传算子优化遗传运算,灵活、有针对性地对父代染色体进行交叉或变异操作,在防止算法陷入局部最优的同时保证种群的更新速度。仿真实验对比结果分析表明所设计的改进算法具有更高效的寻优能力。

兵器科学与技术;整数规划;火力分配;遗传算法;适应度函数

DOI:10.3969/j.issn.1000-1093.2016.01.015

0 引言

火力分配(WTA)是指根据作战目的、战场态势和武器性能等因素,将一定类型和数量的火力单元以某种准则进行分配,攻击一定数量敌方目标的过程。WTA是战场指挥当中的重要环节,是决定作战效果的关键因素[1]。

WTA问题属于一类NP-hard问题。当前国内外研究成果多以对目标的毁伤概率最大为目的,通过智能优化算法,如启发式遗传算法[2]、蚁群遗传算法[3]、模拟退火遗传算法[4]、混合变邻域搜索算法[5]、粒子群算法[6]等对模型进行求解,其中以遗传算法为基础设计搜索算法居多。遗传算法是应用最为广泛的智能优化算法之一,具有很强的全局搜索能力;但其在实际应用中也存在着进化慢、易早熟收敛等问题。实际研究表明,适应度函数的选取和遗传算子调节机制的设置是影响遗传算法性能的关键。适应度函数选取不当将会严重影响算法的计算效率,而传统的遗传算法存在交叉变异概率在种群进化过程中固定不变的不足。

针对具体的工程优化问题,许多学者对算法适应度函数的构建和遗传算子的改进方案进行了研究。文献[7]设计了相对适应度函数和离散重组交叉算子,解决了一类高层结构黏滞阻尼器优化布置问题;文献[8]提出了一种新的适应度函数以解决一类最小属性约简问题;文献[9]将Petri网分析应用于遗传算法的适应度函数设计,用以解决城市交通流优化问题;文献[10]研究了遗传算法的交叉操作,设计了顺序构造交叉算子,提高了生成解的质量;文献[11]设计了一种启发式交叉算子以改善种群质量,加快算法的寻优速度。文献[12]在研究遗传算法求解虚拟机资源调度问题时,设计了新的变异算子,取得了更好地求解结果。

本文针对一类以对目标的毁伤概率最大为目的的WTA问题,采用改进的遗传算法进行求解。通过设计合适的适应度函数以及自适应的变异概率调节机制,提高了算法的寻优能力,避免算法过早地陷入局部极值。

1 WTA问题的数学描述

假设有b种火力单元,分别用Mi(i=1,2,…,b)表示,每种火力单元的数量为mi,且预打击目标共有n个,分别用Tj(j=1,2,…,n)表示;ωj表示第j个预打击目标的威胁度系数;pij表示第i种作战单位对Tj的毁伤概率;令χkj(k=1,2,…,m)为决策变量,表示是否分配第k个火力单元打击第j个目标,若分配则χkj=1,否则χkj=0.所有火力单元必须分配给预打击目标,且每个火力单元只能分配给单个目标。

WTA的目的为根据作战要求,通过攻击最大化地对目标造成毁伤,可描述为

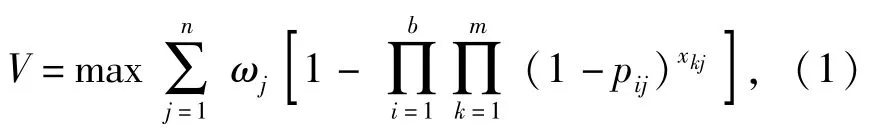
式中:V表示目标函数。此外,模型还应满足毁伤下界约束:

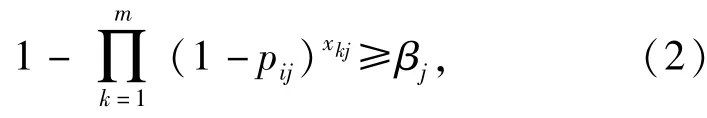
式中:βj表示第j个目标的毁伤下界。

2 基于模拟退火遗传算法的WTA实现

2.1 编码

用智能算法求解WTA问题时,首先要考虑的是所采用的编码方式能不能恰当地表示问题的求解空间以及能否使得算法具有较高的搜索效率。由于火力单元的数目或类型以及目标数均为整数,用整数序列编码表示火力单元与目标的对应状态是自然、合理的方式;而对于不同的WTA问题,根据火力单元总数m与预打击目标总数n的不同,可划分为m＞n,m＜n以及m=n三类情况。因此,所选择的编码方式应在能够描述以上所有3类情况的基础上,尽可能地不产生或较少产生“不合法"的染色体。基于此,搜索解的编码可表示为

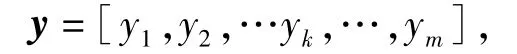
式中:yk为0～n之间的整数,称为元素。yk=j表示将第k个火力单元分配给第j个目标;yk=0表示第k个火力单元没有分配给任一目标。这种编码方式能够描述以上3类情况WTA问题的同时不会产生“不合法"的染色体。

2.2 适应度函数

轮盘赌是最常见的从种群中选择父代染色体的策略,它能够定量地表示染色体之间适应度的差异[13]。在轮盘赌选择方式下,染色体被选中的概率与其适应度值大小紧密相关。本文采用界限构造法[7]设计适应度函数,可表示为

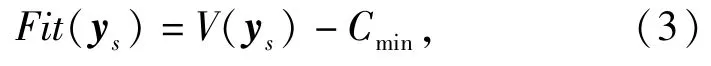
式中:Cmin为V(ys)的最小估计值,需取一个较小的数以保证适应度值非负,例如,对于 (1)式表示的WTA问题来说可选择Cmin=0.同时,Cmin的取值还应尽量使优良染色体能够以较大的概率被选中,从而提高算法优化的计算效率。采用 (3)式计算染色体适应度大小时,一个染色体被选中的几率Pys计算方法如下:

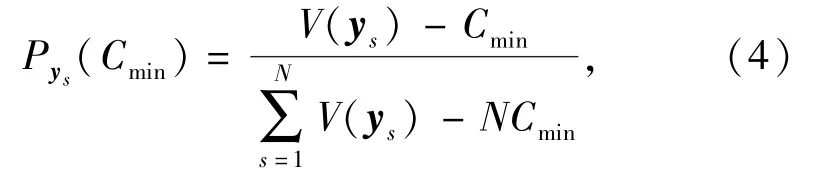
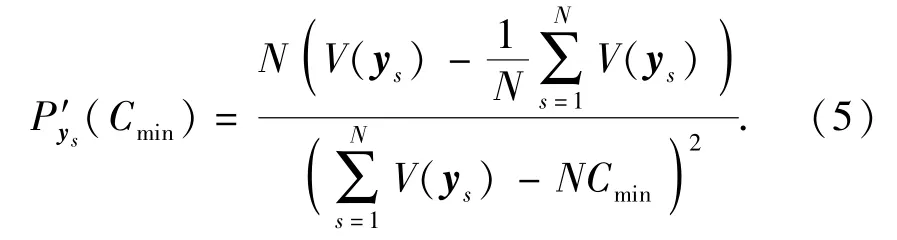
式中:N表示种群大小。Pys对Cmin求导,可得由(5)式可知,当ys为群体中在平均水平之上的优良染色体时,Cmin取值越大,P＇ys(Cmin)越大,即ys被选择的几率就越大。为保证优良染色体在轮盘赌策略下具有最大的选择几率,本文中取,适应度函数可表示为

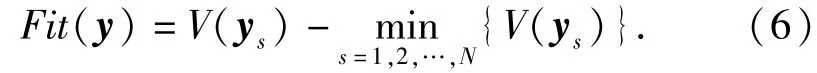
2.3 遗传算子

交叉算子采用多点交叉的方式。对于两个选定的父代染色体y1和y2:

随机选取3个切点,交换切点间的子串,得到新的子代个体y＇1和y＇2:

变异采用简单的替换方式实现。当一个染色体进行变异操作时,随机选取染色体编码中的3个元素,在合理的范围内进行替换:

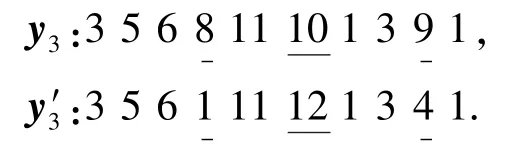
交叉概率pc和变异概率pa的大小是影响算法性能的关键。pc的大小决定种群个体的更新速率,较大的pc能够提高解空间的探索能力,但pc过大时容易导致早熟收敛;pc取值保守会导致算法搜索过程缓慢,不利于种群的进化。pa取值过大会使算法近似于随机搜索,失去遗传算法本身的一些优良特性;pa取值过小容易使种群丢失一些优良的基因。针对这一问题,许多学者研究了自适应调整参数的方法[10-12],取得了一定的成果;但设计的调节机制大都比较复杂,从而耗费大量的计算时间。

本文根据父代染色体之间的相似度来决定是否进行交叉和变异操作。从算法进行交叉和变异操作的目的来看,交叉是为了产生和父代染色体不同的子代染色体,通过比较保留适应度好的个体从而使种群不断进化。但是,当父代染色体之间编码差异很小或没有差异,属于“近亲"时,进行交叉操作产生的子代染色体与父代染色体之间的差异也会很小甚至没有差异;此时,应通过变异操作使得子代染色体与父代染色体之间产生差异,从而增加种群的多样性,扩大对解空间的搜索范围,这也是算法中变异操作行为的目的。总的来说,当父代染色体之间差异度较小时,算法应进行交叉操作;当父代染色体之间差异度较大时,应进行变异操作。用D(y1、y2)表示y1、y2之间的相似度,其值为向量(y1-y2)中0元素的个数。D(y1,y2)越小表示y1、y2之间差异越大,进行交叉操作后得到新的子代染色体几率越高; D(y1,y2)越大表示y1、y2之间差异越小,进行交叉操作越不容易得到新的子代染色体,应进行变异操作增加种群的多样性。基于上述原因,用变异操作阀值φ代替传统的变异概率pa,判断是否进行变异操作;当D(y1,y2)≥φ时,认为选取的父代染色体的相似度足够高,算法进行变异操作。

2.4 最优个体保持策略

本文采用最优个体保持策略对每一代种群中的最优个体进行保护,避免其在之后进行的选择、交叉或变异过程中被破坏。具体方式为:用前一代种群中适应度值最大的染色体代替新一代种群中目标函数值最小的染色体。

2.5 算法描述

采用改进的遗传算法求解WTA问题的具体步骤如下:

步骤1 参数设置。需要设置的参数包括:种群数量N,交叉概率pc,毁伤下界βj,变异操作阀值φ,最大迭代次数Tmax.

步骤2 种群编码及初始化。种群编码采用(3)式表述的方式。通过函数y=ceil(n·rand(m,1))产生初始解,其中ceil和rand分别是Matlab中的取整数和随机数生成命令。

步骤3 计算种群中染色体的适应度值,采用轮盘赌方式选择待交叉的父代染色体。

步骤4 更新种群。从父代染色体中随机选择两个个体y1,y2,计算它们的相似度;若D(y1,y2)≥φ,则进行变异操作;否则,依交叉概率pc进行3切点交叉操作。

步骤5 保留最优个体。计算子代种群的适应度值,用父代种群中的最优个体替换子代种群中适应度值最差的个体。

步骤6 迭代次数加一,判断算法终止条件。若迭代次数达到最大迭代次数Tmax,则输出最优解,结束算法;否则转步骤3.

3 算例仿真和结果分析

为验证改进的遗传算法在求解(1)式类型WTA问题时的优点,采用文献[4]给出的航空兵编队对地攻击WTA模型进行仿真验证,并与该文献中采用的模拟退火遗传算法进行比较。设有3种类型的战机,共m=10架:M1、M2类型战机各有4架,即m1=m2=4;M3类型战机有2架,即m3=2.预打击目标数n=12,目标威胁度以及每种类型战机对各个目标的毁伤概率如表1所示。

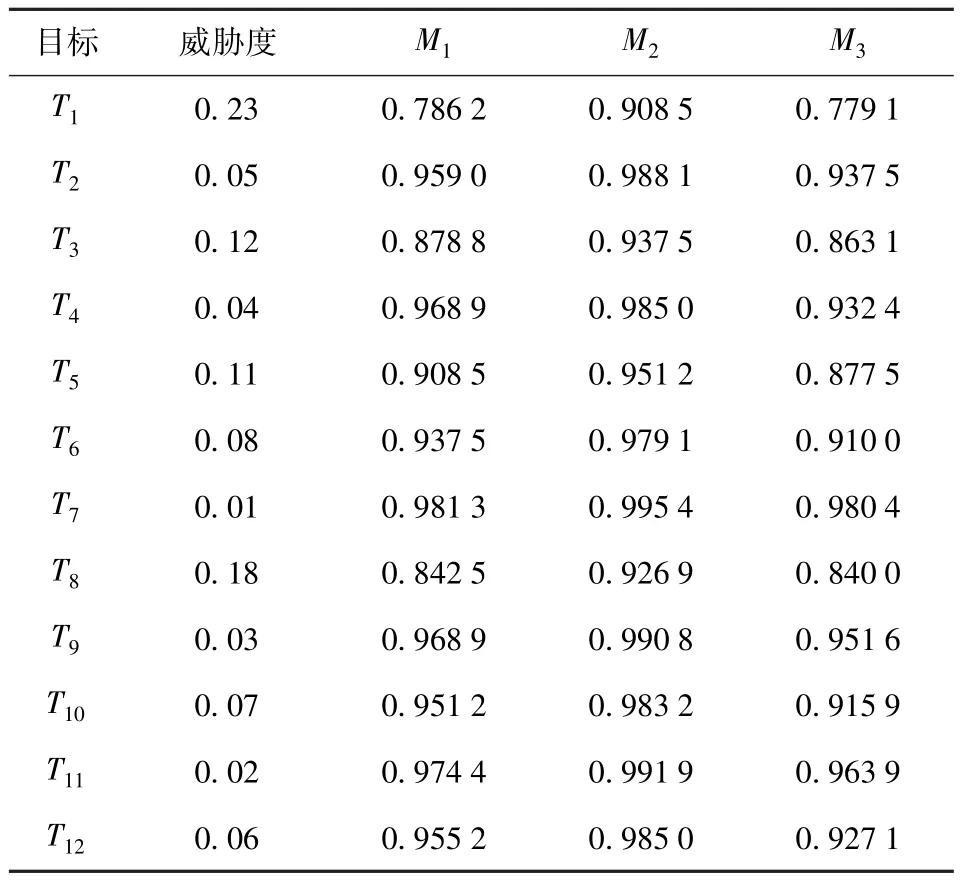
表1 毁伤概率及目标威胁度参数Tab.1 Damage probability and target threat parameters

仿真过程中,遗传算法参数参考文献[4]中给出的数据,设置为:种群数量N=100,交叉概率pc= 0.8,毁伤下界βj=0.8,变异操作阀值φ=7.

3.1 不同适应度函数比较

对算法选择不同适应度函数时的仿真效果进行对比。用仿真实验1表示本文所设计算法,即以(6)式计算适应度值;用仿真实验2表示对比算法,以(3)式计算适应度值。取Cmin=0,最大迭代次数Tmax=30,其它参数设置不变,进行100次仿真计算,结果如图1和表2所示。图1中为直观表现两种算法仿真结果间的差异,分别按从小到大的顺序将适应度值结果重新进行了排列。

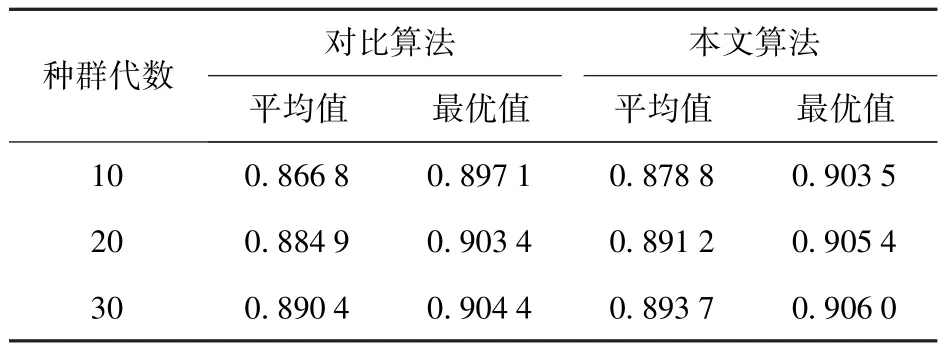
表2 不同适应度值计算方式下的优化结果Tab.2 Optimization results in different fitness value calculation modes

由表2可以看出,本文所提算法的种群适应度值较对比算法具有优势,其中算法初期优势较大,而随着进化次数的增加,优势变得越来越小。这是由于在轮盘赌选择阶段,与对比算法采用的适应度函数相比,(6)式表示的适应度函数能够以更大的概率将种群中的优良染色体选进交配池中,即交配池中父代染色体整体质量较高;在算法初期,种群适应度值增长空间较大,本文算法能够更高效地改善种群质量;而随着进化过程的进行,本文算法逐渐趋于稳定,种群适应度值增长空间逐渐减小,而对比算法种群适应度值仍有一定的增长空间,因此本文算法优势较搜索初期有所缩小。

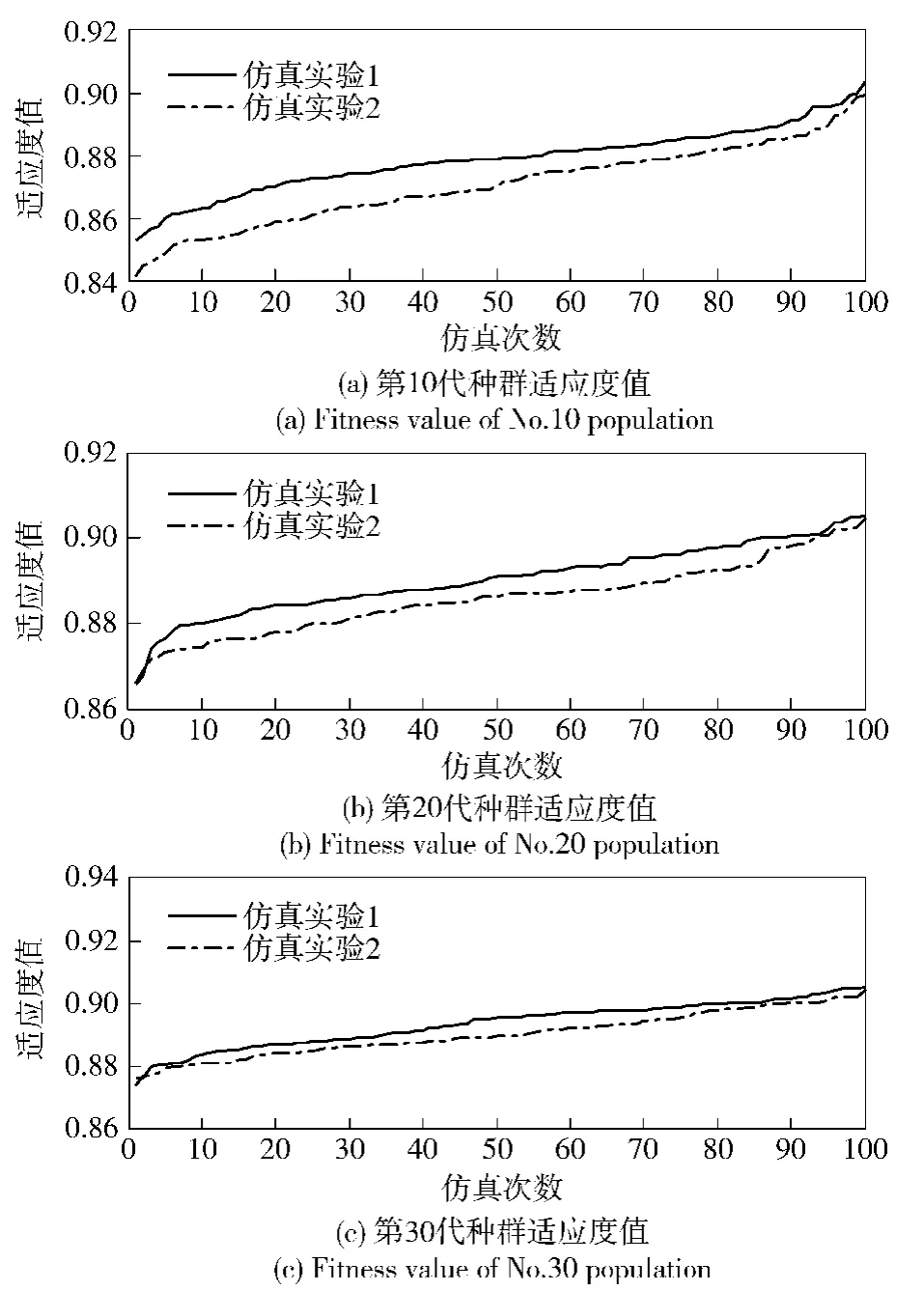
图1 第一组仿真算例结果对比Fig.1 Comparison of simulation results in Group 1

3.2 不同变异算子比较

本节中,采用参考文献[4]中设计的模拟退火遗传算法作为对比算法,用仿真实验3表示,取恒定的变异概率pa=0.1,且采用模拟退火策略避免算法陷入局部极值,退火参数设置为初始温度T0=100,降温系数α=0.99.取最大迭代次数Tmax=50,进行100次仿真计算,结果如图2～图5及表3、表4所示。

由图2和表3可以看出,本文算法的搜索结果更为精确。对比算法中采用固定变异率和模拟退火策略保证种群的多样性,防止算法陷入局部极值,但这两种措施并没有与种群多样性的变化和父代染色体的相似度联系起来。本文算法不需事先确定固定变异率,而是根据具体寻优过程中种群多样性变化和选择的父代染色体之间的相似度决定是否进行变异操作。图3给出了本文算法和对比算法仿真耗时的比较结果,与传统算法相比,本文算法所设计的遗传算子调节机制并不会耗费更多的计算时间。图4给出了每个采用本文算法的仿真实验中总变异次数的统计结果,表3给出了其中的最大值、最小值以及平均值。本文算法中,每次仿真实验会进行2 450次进化操作,由此可知本文算法的变异率大致在0.215～0.562之间,平均为0.317,这与寻优过程中种群收敛至最优值的速度有关:种群越快地接近最优值,每代更新时变异次数就越多。图5给出了采用本文算法的一次仿真实验种群更新过程中进化代数与变异次数的关系曲线。可以看出,开始阶段变异次数较少,这是由于此时种群多样性较高,选择的父代染色体之间相似度较小的缘故;随着种群的不断更新,种群中的个体越来越接近最优解,种群多样性变得较差,选择相似度较高的父代染色体进行交配的概率越来越大,因此变异操作次数也越来越多。表4给出了本文算法得到的最优攻击分配方案,最优值为0.906 0.通过以上实验数据可知,本文所设计的变异算子能够在不影响计算耗时的情况下,取得更好的优化结果。

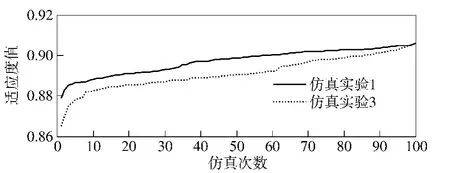
图2 第二组仿真算例结果对比Fig.2 Comparison of simulation results in Group 2

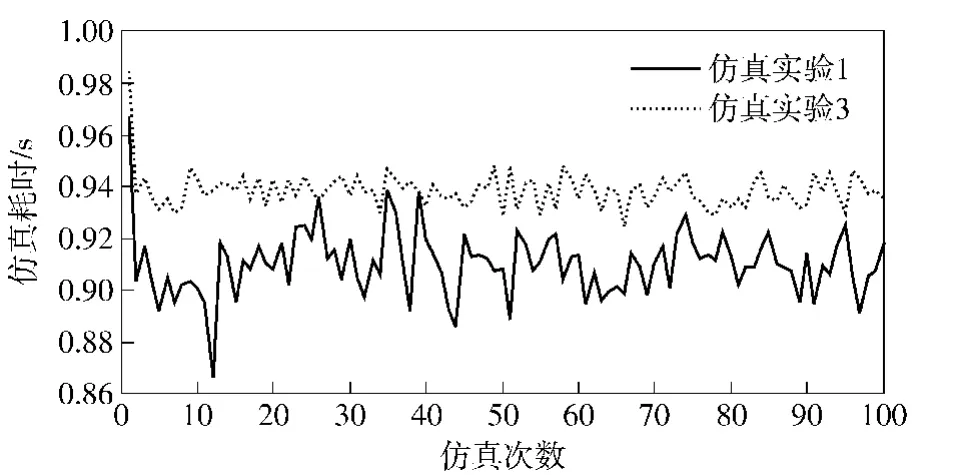
图3 仿真耗时比较Fig.3 Comparison of simulation times

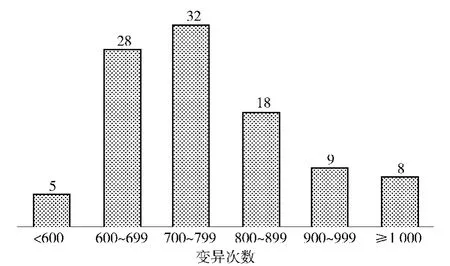
图4 本文算法总变异次数统计Fig.4 Total mutation times statistics of the proposed algorithm

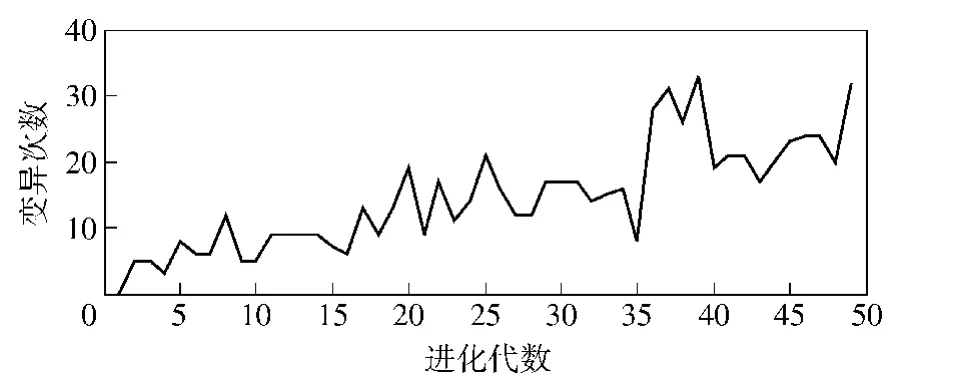
图5 种群更新过程中变异操作次数Fig.5 Mutation operation times in population regeneration process

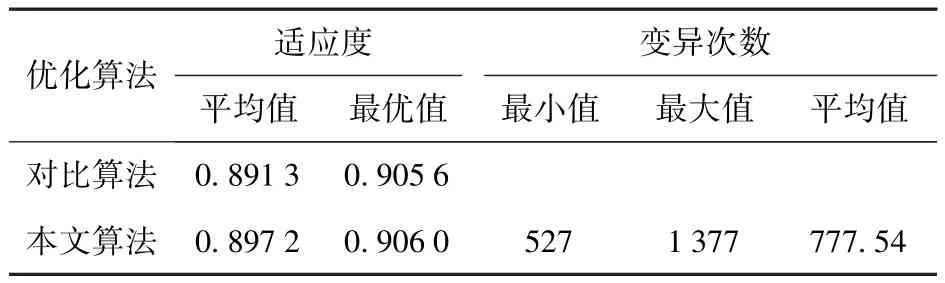
表3 不同变异算子下的优化结果Tab.3 Optimization results in different variation operators

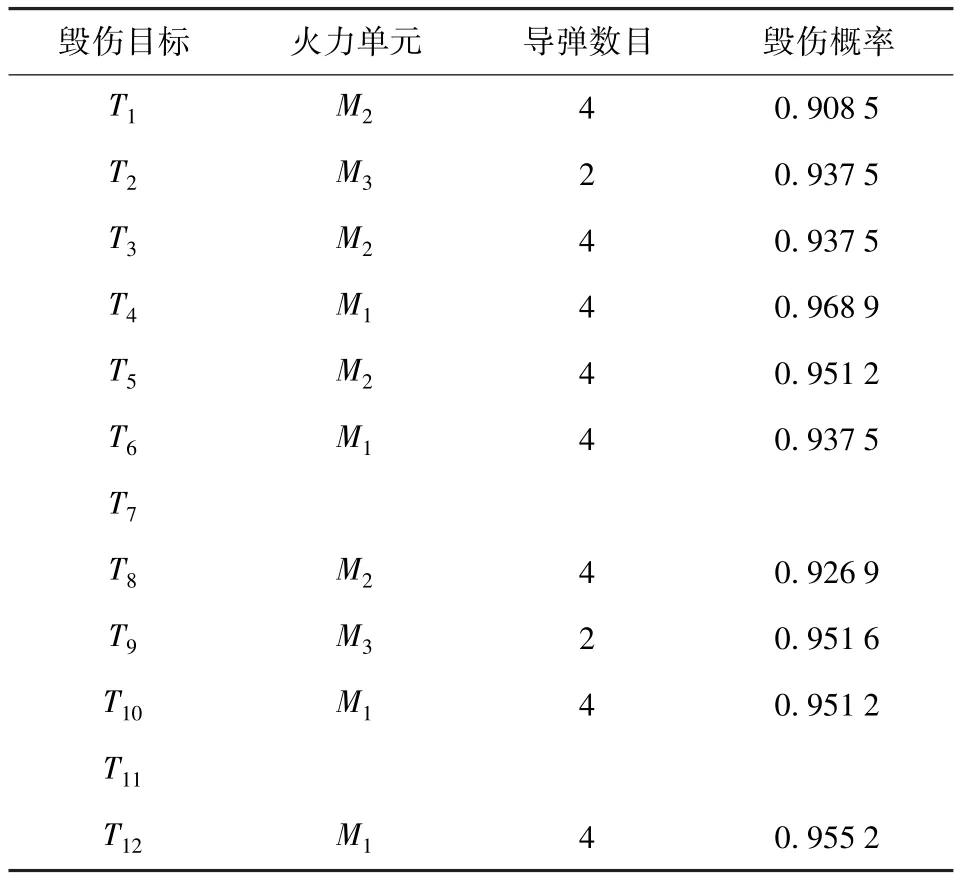
表4 本文算法得到的最优攻击分配Tab.4 Optimal attack distribution of the proposed algorithm

4 结论

本文针对一类以对目标的毁伤概率最大为目的的WTA问题,提出了一种改进的遗传算法,并通过仿真实验得到了以下结论:

1)适应度函数的选择影响算法的寻优精度。本文构造的适应度函数较传统的界限构造法能够提高优秀染色体被选中的概率,从而提高了种群的质量,对算法寻优能力产生积极影响。

2)根据寻优过程中种群多样性的变化,有针对性地选择交叉或变异操作,仿真结果表明所设计的遗传算子较固定不变的遗传算子操作模式更为合理,效率更高。

References)

[1]张蛟,王中许,陈黎,等.具有多次拦截时机的防空火力分配建模及其优化方法研究[J].兵工学报,2014,35(10):1644-1650.ZHANG Jiao,WANG Zhong-xu,CHEN Li,et al.Modeling and optimization on antiaircraft weapon-target assignment at multiple interception opportunity[J].Acta Armamentarii,2014,35(10): 1644-1650.(in Chinese)

[2]Bayrak A E,Polat F.Employment of an evolutionary heuristic to solve the target allocation problem efficiently[J].Information Sciences,2013,222:675-695.

[3]Zhang J,Wang X,Xu C,et al.ACGA algorithm of solving weapon-target assignment problem[J].Open Journal of Applied Sciences,2013,2(4):74-77.

[4]贺小亮,毕义明.基于模拟退火遗传算法的编队对地攻击WTA建模与优化[J].系统工程与电子技术,2014,36(5): 900-904.HE Xiao-liang,BI Yi-ming.Modeling and optimization of formation air-to-ground attack fire distribution based on simulated annealing genetic algorithm[J].Systems Engineering and Electronics,2014,36(5):900-904.(in Chinese)

[5]Tokgöz A,Bulkan S.Weapon target assignment with combinatorial optimization techniques[J].International Journal of Advanced Research in Artificial Intelligence,2013,2(7):39-50.

[6]Leboucher C,Shin H S,Le Mènec S,et al.Novel evolutionary game based multi-objective optimisation for dynamic weapon target assignment[C]//Preprints of the 19th World Congress:The International Federation of Automatic Control.Cape Town,South Africa:IFAC,2014:3936-3941.

[7]燕乐纬,陈洋洋,周云.基于数字序列编码遗传算法的高层结构黏滞阻尼器优化布置[J].振动与冲击,2015,34(3): 101-107.YAN Le-wei,CHEN Yang-yang,ZHOU Yun.Optimal positioning of viscous dampers in tall buildings based on digital sequence conding genetic algorithm[J].Journal of Vibration and Shock,2015,34(3):101-107.(in Chinese)

[8]Ye D Y,Chen Z J,Ma S L.A novel and better fitness evaluation for rough set based minimum attribute reduction problem[J].Information Sciences,2013,222:413-423.

[9]Henrique D,Regiane D S B,Norian M,et al.Optimizing urban traffic flow using genetic algorithm with Petri net analysis as fitness function[J].Neurocomputing,2014,124:162-167.

[10]Zakir H Ahmed.Genetic algorithm for the traveling salesman problem using sequential constructive crossover operator[J].International Journal of Biometrics and Bioinformatics,2010,3(6):96-105.

[11]于莹莹,陈燕,李桃迎.改进的遗传算法求解旅行商问题[J].控制与决策,2014,29(8):1483-1488.YU Ying-ying,CHEN Yan,LI Tao-ying.Improved genetic algorithm for solving TSP[J].Control and Decision,2014,29(8): 1483-1488.(in Chinese)

[12]Gu J H,Hu J H,Zhao T H,et al.A new resource scheduling strategy based on genetic algorithm in cloud computing environment[J].Journal of Computers,2012,7(1):42-52.

[13]汪定伟,王俊伟,王洪峰,等.智能优化算法[M].北京:高等教育出版社,2007.WANG Ding-wei,WANG Jun-wei,WANG Hong-feng,et al.Intelligent optimization methods[M].Beijing:Higher Education Press,2007.(in Chinese)

Improved Genetic Algorithm for Solving Firepower Distribution

DONG Chao-yang1,LU Yao1,WANG Qing2
(1.School of Aeronautic Science and Engineering,Beihang University,Beijing 100191,China; 2.School of Automation Science and Electrical Engineering,Beihang University,Beijing 100191,China)

An improved genetic algorithm for solving firepower distribution is proposed.The fitness function is constructed based on relative value of objective function.Compared with the conventional finitude construction method,this measure can incarnate the differences among the chromosomes more significantly and the fine chromosomes are selected more easily,thus improving the convergence precision of algorithm.The heuristic genetic operator based on the similarity of father chromosomes is used to optimize the genetic operation and do crossover or mutation to the father chromosomes with agility and pertinence.It can prevent the local optimization and guarantee the optimization speed of population.The contrast results of simulation examples show that the improved algorithm have more efficient search ability.

ordnance science and technology;integer programming;firepower distribution;genetic algorithm;fitness function

N945.25

A

1000-1093(2016)01-0097-06

2015-06-10

国家自然科学基金项目(61273083、61374012)

路遥(1987—),男,博士研究生。E-mail:luyaosacred@126.com;董朝阳(1966—),男,教授,博士生导师。E-mail:dongchaoyang@buaa.edu.cn