寻找Span n序列的方法的改进
2016-11-08陈克非
屈 哲 陈克非
1(上海交通大学计算机科学与工程系 上海 200240)2(杭州师范大学理学院 浙江 杭州 310036)3(保密通信重点实验室 四川 成都 610041)
寻找Span n序列的方法的改进
屈哲1,3陈克非2,3
1(上海交通大学计算机科学与工程系上海 200240)2(杭州师范大学理学院浙江 杭州 310036)3(保密通信重点实验室四川 成都 610041)
de Bruijn序列是一个周期为2n的0、1序列,去掉n阶de Bruijn序列中连续的n个0中的一个得到一个周期为2n-1的序列,称为span n序列。一个n阶de Bruijn序列的线性复杂度在2n-1+n和2n-1之间,然而对应的span n序列的线性复杂度可能降为n。所以span n序列的线性复杂度成为了衡量一个de Bruijn序列好坏的重要标准,因此研究生成高线性复杂度的span n序列的方法是非常有意义的。研究文献[6]中提出的基于特殊函数和非线性反馈移位寄存器寻找span n序列的方法,发现span n序列与参数t的无关性,并基于此提出了几种改进算法。对各种算法进行横向比较,并指出了每种算法的局限和优点,以及今后可能的改进。
非线性反馈移位寄存器de Bruijn序列span n序列
0 引 言
近些年,在伪随机序列生成器。流密码和一些轻量级的分组密码等领域,非线性反馈移位寄存器NLFSR(Nonlinear Feedback Shift Register)受到了越来越多的关注。基于非线性反馈移位寄存器的密码在一些需要高效硬件实现和高吞吐量等受限制的环境下表现出良好的实用价值,发挥着重要的作用。
在流密码中,加密使用的是将明文和密钥流以比特为单位进行那个异或操作来产生密文。流密码要求密钥流是一个随机的比特流,而NLFSR恰好满足此要求。最大周期NLFSR序列拥有周期长,平衡性好,游程分布均匀,良好的二阶自相关性,低互相关性,高线性复杂度等密码学性质。在eSTREAM[1]流密码项目中有如Grain和Trivium基于NLFSR的密码设计。
虽然NLFSR拥有如此好的随机特性,但是一般给定NLFSR,目前并不存在一个通用的方法来计算该NLFSR周期和其他相关的序列特征。生成指定阶数的最大周期NLFSR序列目前也是一个开放的问题。目前使用暴力枚举的方法,可以生成一系列n<25的最大周期NLFSR序列[2],结合特殊制作的硬件可以生成n=25和n=27的最大周期NLFSR序列[3]。
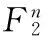
本文研究了Kalikinkar Mandal在2012年提出的一种基于WG函数的搜索span n序列的方法[6],对该方法做了几种不同方面的改进,并对原方法及改进方法做了数据分析和比较。
1 反馈移位寄存器和寻找span n序列的方法
本节将介绍反馈移位寄存器的一些基础知识,并且研究基于非线性反馈移位寄存器和WG函数的寻找span n序列的方法。
1.1非线性反馈移位寄存器
移位寄存器是一种以时间脉冲为触发条件的控件,每经过一个脉冲,该器件移动一个比特并且在输出端输出。反馈移位寄存器简称FSR(Feedback Shift Register)是指将前一状态的输出再次用作输入的一种移位寄存器。如果输出为输入寄存器的线性函数,那么叫作线性反馈移位寄存器简称LFSR(Linear Feedback Shift Register),如果是输入寄存器的非线性函数,那么叫做非线性反馈以为寄存器简称NLFSR(Nonlinear Feedback Shift Register)。
通常FSR可以用反馈函数来表示:
xi=f(xi-1,xi-2,…,xi-n)
一般的FSR结构如图1所示。

图1 FSR结构示意图
此处,n表示寄存器个数,xi表示第i个脉冲时的输出状态,f为反馈函数。其中线性和非线性是反馈函数f的特征。xi通常取值为0或1,所有的运算均在模2的意义下进行,即在有限域F2中。所以通常的加法变为0+0=0,0+1=1+0=1,1+1=0,与计算机理论中的异或运算结果相同。在后面的文章中,反馈函数里的“+”均表示计算机里的“异或”。
一个典型的LFSR方程为:xi=xi-1+xi-3
由反馈函数知相邻的三个比特唯一决定了下一个比特,与之前的状态无关,如果将(xi-2,xi-1,xi)作为状态,状态转移的关系如表1所示。

表1 LFSR状态转移
一个典型的NLFSR方程为:xi=1+xi-3+xi-1+xi-1xi-2
其中常数项1和二阶项xi-1xi-2均为非线性项。状态转移表如表2所示。

表2 NLFSR状态转移
FSR经过足够多的时间脉冲可以得到一个足够长的序列,序列中连续的n位也产生了足够多的n元组状态,因为n元组最多只有2n个,所以该序列最终会不断地重复一个片段。重复片段的最小长度叫做这个序列的周期,也为该FSR的周期。所以一个FSR的最大周期为2n,对于LFSR,因为f(0,…,0)=0,所以最大周期为2n-1,称作m序列。对于NLFSR,2n是可以取到的,称作M序列,也叫作de Bruijn序列。
LFSR背后的数学理论已经研究得非常清楚,可以根据阶数构造出m序列LFSR。NLFSR的理论目前并不明确,给定反馈函数现在并没有有效的算法确定其周期,给定阶数n,现在也没有有效的算法构造出最大周期序列。关于NLFSR,目前的问题还都非常开放,还有很多值得研究和挖掘的东西。
在FSR中,如果将每一个n元组状态看作一个点,能够转移的状态之间连边,那么每一个状态有两条入边,两条出边,按照这种方式构成的图称作de Bruijn图。图上的任意一条路径都形成了一个二元序列,其中Hamiltonian路径长度最长,为2n,形成的序列称为de Bruijn序列,即每一个n元组均出现一次的序列。将de Bruijn序列中连续的n个0中的一个去掉得到的序列叫做modified de Bruijn序列,也称作span n序列。m序列即为span n序列的一个子集。span n序列具有非常好的密码学性质,但是目前并没有通用生成span n序列的方法。本文将在第2节研究一些寻找span n序列的方法。
衡量一个序列性质好坏的一个重要指标为线性复杂度,即可以生成该序列的所有LFSR中阶数最小的那一个的数值。已知序列可以使用Berlekamp-Massey算法计算其线性复杂度。
1.2基于特殊函数寻找span n序列的方法
Kalikinkar Mandal在2012年提出了一种基于WG函数的搜索span n序列的方法[6]。
Welch-Gong(WG)变换序列是周期为2n-1的具有二阶自相关性的二元序列。Golomb,Gong和Gaal在1998年发现WG变换序列并且验证了5≤n≤20的情况[7]。不久之后,No等人发现了另外一个构造WG序列的方法,并且验证了5≤n≤23的情况[8]。Dillon在1998年首次证明了n为奇数的情况[9],Dobbertin和Dillon在1999年又证明了n为偶数的情况[10],使得整个结果完整。
设n不被3整除,那么阶数为n的WG变换函数为:
如果n=3k-1,记:
q1=2k+1
q2=22k-1+2k-1+1
q3=22k-1-2k-1+1
q4=22k-1+1
如果n=3k-2,记:
q1=2k-1+1
q2=22k-2+2k-1+1
q3=22k-2-2k-1+1
q4=22k-1-2k-1+1
那么WG变换函数为:
WGP(x)=h(x+1)+1
其中:
h(x)=x+xq1+xq2+xq3+xq4
定义:
fd(x)=Tr(h(xd))d∈Dt
其中:
Tr(x)=x+x2+…+x2n-1
Dt={d|gcd(d,2n-1)=1}模2n-1的2-分圆陪集首
记Fn表示n阶有限域,那么h(x)为从F2n到F2n的函数,Tr(x)为从F2n到F2的函数,所以fd(x)为从F2n到F2的函数。利用fd(x)有如下构造NLFSR的方法。
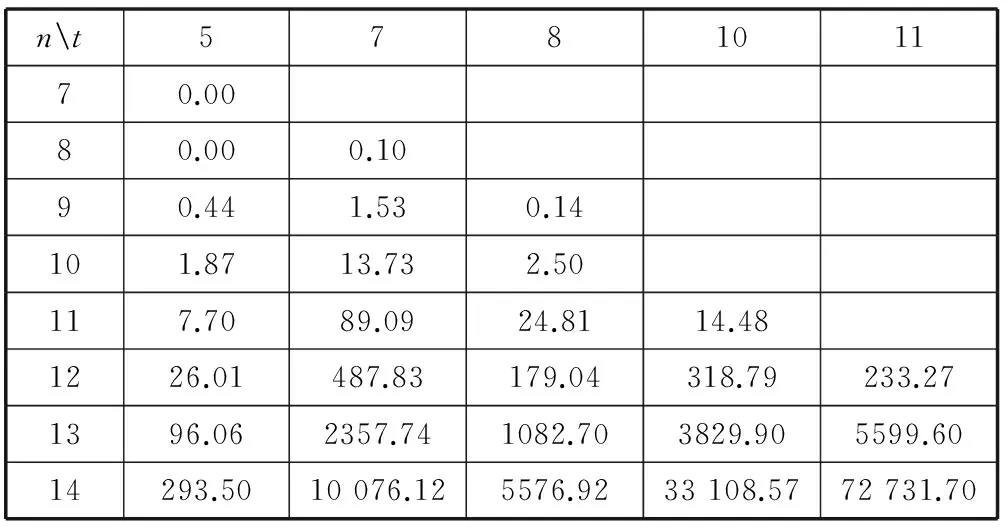
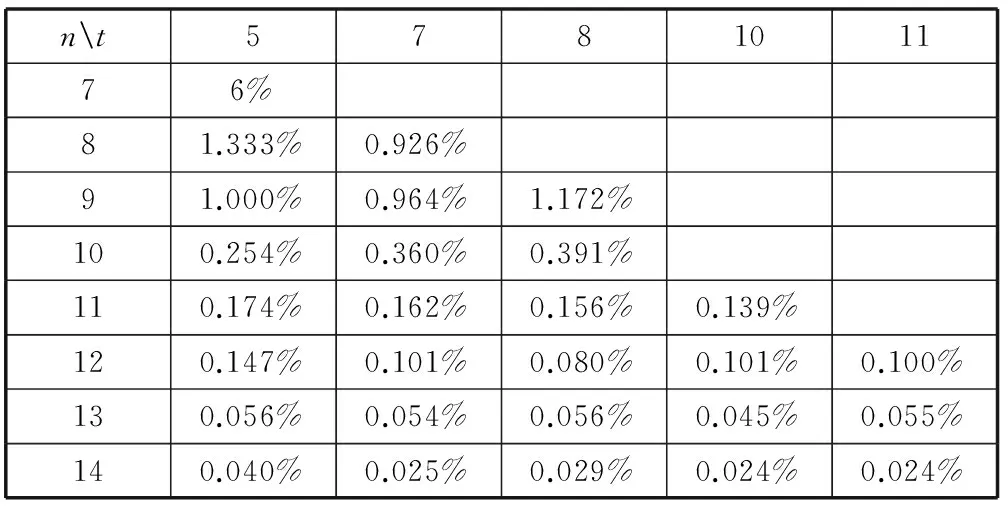
对于n阶NLFSR,记寄存器编号为0,1,…,n-1,选择寄存器t元组(r1,r2,…,rt)满足0 xn+k=xk+fd(Rk)Rk=(xr1+k,xr2+k,…,xrt+k) NLFSR构造如图2所示。 图2 使用WG函数构造的NLFSR结构图 按照这种方法构造的NLFSR由以下五个参数组成: n—— 寄存器个数 d—— 决定数 t——在n-1个寄存器中选择t个 t-tap——(r1,r2,…,rt),具体选择了哪t个 pp——本原多项式,决定了反馈函数运算的有限域 固定n和t,暴力枚举剩余的参数d,t-tap,pp得到一个NLFSR后,然后验证其周期,如果为2n-1,那么便找到了一个span n序列。 (1) 本文提出了几种基于文献[6]的寻找NLFSR的方法。基本算法为枚举+验证,我们每次根据枚举算法找到一个参数组(t-tap,d,pp),然后验证该NLFSR产生的序列是否为我们所需要的span n序列。在验证部分,目前并没有有效的算法,本文采取使用按照NLFSR规则生成序列并验证的方法。所以我们的改进着眼于枚举部分,通过减小搜索空间来提高搜索效率。 2.1朴素暴力搜索 这是文献[6]所提出的算法,也是本文所研究和需要改进的算法。记为去掉使得为线性函数的元素的集合。 算法1朴素暴力搜索 输入:寄存器个数n,选择出的寄存器个数t(t 输出:所有生成span n序列的NLFSR,以参数组(t-tap,d,pp)给出。 算法: (1) 枚举度为t的本原多项式pp,确定运算的有限域F2t; (3) 枚举t-tap,除去0号寄存器,在1到n-1号寄存器中选择t个; (4) 验证(t-tap, d, pp)对应的NLFSR的周期,若为2n-1,则输出该NLFSR。 空间复杂度:因为NLFSR最大周期为2n-1,所以空间复杂度为O(2n)。 该算法的缺点是在t=4时找到的span n序列线性复杂度过小,文献[6]中也没有讨论t=4的情况。在n较大时,随着t的增加,搜索空间急剧增大,不利于span n序列的查找。 2.2基于GPU并行搜索 使用NVIDIA提出的CUDA[11]并行搜索。给定(n,t),通过将参数组(t-tap,d,pp)分配到不同的线程块上,来加速枚举过程。 算法2基于GPU并行搜索 输入:寄存器个数n,选择出的寄存器个数t(t 输出:所有生成span n序列的NLFSR,以参数组(t-tap, d, pp)给出。 算法: (1) 确定线程块各个维度大小,在每一个线程块中均执行(2)、(3)、(4)、(5); (2) 枚举度为t的本原多项式pp,确定运算的有限域F2t; (4) 枚举t-tap,除去0号寄存器,在1到n-1号寄存器中选择t个; (5) 验证(t-tap,d,pp)对应的NLFSR的周期,若为2n-1,则输出该NLFSR。 在CUDA并行编程框架里,线程块是三维的,所以可以将t-tap,d,pp三个参数刚好分配到不同的维度上。 空间复杂度:,记线程块个数为N,则空间复杂度为N×O(2n)=O(N·2n)。 并行是加速枚举过程的一个有效办法,但缺点是对于空间消耗过大,对于单台机器很快就会超过机器空间限制。可能的改进方法是将不同的参数(t-tap,d,pp)分配到不同的机器上,因为问题的特殊性,可以舍弃一些并行框架的限制,采取“分开即并行”的策略。 2.3对搜索空间大小设定阈值搜索 通过式(1)可以根据(n,t)计算出所需的计算量,所以我们可以预先指定一个阈值L,只有当计算量不大于L时我们才进行搜索,否则跳过。这样对于特定的n我们有选择地去找t来进行后续的搜索。 算法3对搜索空间大小设定阈值搜索 输入:寄存器个数n。 输出:给出部分生成span n序列的NLFSR,以参数组(t,t-tap, d, pp)给出。 算法: (1) 设定阈值L; (2) 枚举t; (3) 由n,t计算Spacen,t,若Spacen,t (4) 枚举度为t的本原多项式pp,确定运算的有限域F2t; (6) 枚举t-tap,除去0号寄存器,在1到n-1号寄存器中选择t个; (7) 验证(t-tap,d,pp)对应的NLFSR的周期,若为2n-1,则输出该NLFSR。 空间复杂度:O(2n)。 时间复杂度:因为只有当搜索空间小于L时才进行搜索,所以时间复杂度为O(nL)。 如果阈值L设定的过小的话,当n比较大时,t最多只能取到4,而这种情况搜索出的span n序列的线性复杂度偏低。 2.4针对t=4的情况扩大搜索空间寻找高线性复杂度span n序列 由式(1)可知,t越小枚举量越小,文献[6]里t的最小值取为5。我们取t=4运行算法2.1,发现在搜索量更小的情况下反而找到了更多的span n序列,但是找出来的序列线性复杂度都不高,在2n附近。 为了提高所找到span n序列的线性复杂度,我们在选出t-tap后对这些寄存器按照事先的约定做一个置换,然后再运行后面的算法。这样搜索空间的大小变为之前的t!=4!=24倍,但是找到了高线性复杂度的span n序列,集中在2n-1。 算法4针对t=4的情况扩大搜索空间寻找高线性复杂度span n序列 输入:寄存器个数n。 输出:给出部分生成span n序列的NLFSR,以参数组(p4,d,pp)给出。 算法: (1) 枚举度为t=4的本原多项式pp,确定运算的有限域F2t; (3) 枚举四元组p4=(r1,r2,r3,r4),其中ri互不相同,0 (4) 验证(p4,d,pp)所构成的NLFSR的周期,如果为span n序列,那么输出(4,d,pp); p4的作用相当于在2.1节中的t-tap选择出来后加入了一个排列,将t元向量中元素的位置改变。 空间复杂度:O(2n)。 该算法优点是时间复杂度小,并且可以找到高线性复杂度span n序列。缺点为当n增大后span n序列越来越少。 2.5对部分寄存器添加置换操作,进行a+b搜索 将2.1节和2.4节结合起来形成a+b搜索算法。t不变,随着n的增大,搜索效率降低,我们可以通过增加排列的方法来增大搜索空间提高找到的span n序列数量。然而通过增加排列所得到的搜索空间是之前的t!倍,这个当t增大时并不利于搜索,我们可以采取固定t中的b个,而对剩余的a=t-b个做排列,这样仍然可以大幅度提高找到的span n序列的数量。 算法5对部分寄存器添加置换操作,进行a+b搜索 输入:寄存器个数n,参与排列的寄存器个数a,不动的寄存器个数b(t=a+b)。 输出:给出部分生成span n序列的NLFSR,以参数组(pa,pb,d,pp)给出。 算法: (1) 枚举度为t的本原多项式pp,确定运算的有限域F2t; (3) 枚举参与置换的寄存器a元组pa; (4) 枚举不参与置换的寄存器b元组pb; (5) 验证(pa,pb,d,pp)所构成的NLFSR的周期,如果为span n序列,那么输出(4,d,pp); 空间复杂度:O(2n)。 该算法可以弥补算法2.1节和算法2.4节的不足,在维持t=a+b较小的情况下,保证搜索空间不会过大,然后通过对a个寄存器做置换操作,来增加span n序列的数量。 2.6随机枚举参数进行搜索 采用随机化的方法来枚举参数,然后验证。将问题转化为给定n,找到一个n阶span n序列,不同于之前遍历整个搜索空间找到所有span n序列的算法。 算法6随机枚举参数进行搜索 输入:寄存器个数n。 输出:给出部分生成span n序列的NLFSR,以参数组(t-tap,d,pp)给出。 算法: (1) 随机选组参数(t-tap, d, pp); (2) 验证(t-tap,d,pp)对应的NLFSR的周期,若为2n-1,则输出该NLFSR。 空间复杂度:O(2n)。 该算法不再拘泥于某个t,然后针对(n,t)进行搜索,而是在整个搜索空间中进行随机化枚举,有效避免了搜索了整个(n,t)空间,却没有找到任何一个span n序列的情况,大大提高枚举的效率。 本节将列举一些第2节提出的几种算法的一些实验数据并对数据进行相关的分析。 3.1朴素暴力算法 本小节叙述了文献[6]中算法的一些基本特征。 根据式(1),搜索空间分布如表3所示。 表3 (n,t)搜索空间大小 经过实验得到搜索消耗时间如表4所示,单位为秒。 表4 (n,t)搜索时间 通过表3和表4可以看到搜索空间和搜索时间两者的走向基本一致,这也从另一个侧面说明了第3节中用搜索空间来描述时间复杂度的合理性。 搜索到span n序列的数量如表5所示。 表5 参数(n, t)下span n序列数量 对于每一个(n,t),考察span n序列所占搜索空间的比例,如表6所示。 表6 参数(n, t)下span n序列数量占总搜索空间比例 随着n的增加,span n序列比例减小,然而固定n,对于不同的t,span n序列比例相对稳定,这也为算法6提供了一定数据上的依靠。 3.2基于GPU并行搜索 并行搜索的瓶颈在于每一个线程块都需要O(2n)的空间,这在n比较大时是无法接受的。对于较小的n,因为并行的各种协调性工作,其搜索效率并不比算法1来得更好。 3.3对搜索空间大小设定阈值搜索 根据表6可知,对于相同的n,搜索不同的t搜索效率大致相同,但是不同的t对应的搜索空间大小是不同的,这启发我们可以预先按照搜索空间大小排序,然后按照给定的一个阈值L只对搜索空间小于L的t进行搜索。由于搜索效率并未损失而搜索空间由于阈值的限制又相对较小,这使得搜索可以更快的进行。 表7为L=1010时的搜索数据。 表7 阈值 搜索到的span n序列数量 在n较大时,t非常小,只能取2或4。虽然能够获得span n序列,但是序列的线性复杂度都较低,由Berlekamp-Massey算法计算得到序列的线性复杂度在2n附近。 3.4针对t=4的情况扩大搜索空间寻找高线性复杂度span n序列 算法4是对算法3的改进。表8为t=4 span n序列所占总搜索空间的比例。 表8 t=4时span n序列占总搜索空间比例 t=4时span n序列相比t>4时有大幅提升,但是序列线性复杂度过低。我们所做的是在提取出t-tap后再进行一个置换操作,然后运行之后的运算,最后筛选出线性复杂度高的span n序列。 表9为添加置换操作后找到的高线性复杂度span n序列数量。 表9 添加置换后t=4高线性复杂度span n序列数量 经过置换后的span n序列复杂度在2n-1附近,相比于之前的2n有大幅提高。遗憾的是在n=17没有找到高线性复杂度span n序列。 3.5对部分寄存器添加置换操作,进行a+b搜索 算法5为算法1和算法4的结合。表10为固定b=1个寄存器为1号寄存器,剩余a=4个寄存器做置换的结果,即4+1的一个部分结果,因为并未对b=1个寄存器做枚举。 表10 4+1与传统t=5时span n序列数量对比 虽然并未对b=1个寄存器做枚举,但是表10已足够说明4+1方式可以搜索到更多的span n序列。 3.6随机枚举参数进行搜索 随机化搜索基于表6的结果。因为不同的t所含span n序列比例基本不变,我们可以认为span n序列在整个参数空间内均匀分布,这启发我们可以随机化参数然后验证寻找span n序列。问题也变为给定阶数n,寻找一个span n序列NLFSR。 表11为搜索到的span n序列NLFSR与所耗时间。 表11 使用随机化搜索到一个span n序列的时间 算法1是最为朴素的算法,也是其他算法的基础,缺点是当n较大时,搜索空间太大。通过实验3.1得到的数据可以看到对于不同的t,span n序列的比例是相对稳定的,即搜索效率基本不变,基于此发展出了算法3和算法6。在算法3中我们预先对不同的t计算其搜索空间,然后只对小于某阈值L的t进行下一步搜索,因为之前基于搜索效率不变的发现,这样的搜索是有效的。span n序列在不同的t上分布相对稳定可以认为span n序列在参数(t-tap, pp, d)上分布均匀,因此可以采用随机方法来进行搜索,实验3.6的数据也证明了这一点,找到了文献[6]中未涉及的n=21的一组span n序列,这只是在普通PC机上算出来的结果,可以认为如果使用计算能力更高的PC机的话,结果可能会更好。基于算法3中t=4时span n序列比例的异常即线性复杂度过小的事实,发展出了算法4。算法4利用t=4时搜索空间小的优势,添加置换操作,从而在仍然维持小搜索空间的情况下找到了更多的span n序列。在n较大时,算法4失去了作用,然而和算法1结合,发展出了算法5。我们仍然需要维持t较小,使得搜索空间维持在可以计算的范围,然后只对部分寄存器做算法4中的置换操作。由实验3.5的结果可知算法5相比于算法1在相同的t的情况下,找到了更多的span n序列。 本文对文献[6]提出的搜索span n序列的方法做了研究和改进。针对t=4时span n线性复杂度低的情况添加置换做了改进。基于表6的结果提出了随机化搜索的方法,该方法可以对n>20的情况作处理,这点优于相比于原始算法并给出了n=21时的一组数据。 关于算法1肯定还有很多值得探讨的问题,关于NLFSR也还有很多开放的问题值得去探索。 [1] eSTREAM:the ECRYPT Stream Cipher Project[EB/OL].http://www.ecrypt.eu.org/stream/. [2] Dubrova E.A list of maximum-period NLFSRs[R].Cryptology ePrint Archive,Report 2012/166 (2012).http://eprint.iacr.org/2012/166. [3] Rachwalik T,Szmidt J,Wicik R,et al.Generation of Nonlinear Feedback Shift Registers with special-purpose hardware[C]//Communications and Information Systems Conference (MCC), 2012 Military,1-4.[4] Chan A H,Games R A,Key E L.On the complexities of de Bruijn sequences[J].Journal of Combinatorial Theory,Series A,1982,33(3):233-246. [5] Mayhew Gregory L,Solomon W Golomb.Linear spans of modified de Bruijin sequences[J].IEEE transactions on information theory,1990,36(5):1166-1167. [6] Mandal K,Gong G.Probabilistic Generation of Good Span n Sequences from Nonlinear Feedback Shift Registers[R].CACR Technical Report (2012). [7] No J S,Golomb S W,Gong G,et al.Binary Pseudorandom Sequences of Period 2n-1 with Ideal Autocorrelation[J].IEEE Transactions on Information Theory,1998,44(2):814-817. [8] No J S,Chung H,Yun M S.Binary pseudorandom sequences of period 2m-1with ideal autocorrelation generated by the polynomial zd+(z+1)d[J]. InformationTheory, IEEE Transactions on,1998,44(3):1278-1282. [9] Dillon J F.Multiplicative difference sets via additive characters[J].Designs,Codes and Cryptography,1999,17(1-3):225-235. [10] Dillon J F,Dobbertin H.New cyclic difference sets with Singer parameters[J].Finite Fields and Their Applications,2004,10(3):342-389. [11] Nvidia C.What is CUDA[EB/OL].[2013-5-1].http://www.nvidia.com/object/cuda_home_new.html. IMPROVEMENT IN SEARCHING METHOD OF SPAN N SEQUENCES Qu Zhe1,3Chen Kefei2,3 1(DepartmentofComputerScienceandEngineering,ShanghaiJiaoTongUniversity,Shanghai200240,China)2(SchoolofScience,HangzhouNormalUniversity,Hangzhou310036,Zhejiang,China)3(ScienceandTechnologyonCommunicationSecurityLaboratory,Chengdu610041,Sichuan,China) de Bruijn sequence is a binary sequence with length 2n, by removing one zero from consecutive n zero of n-stage de Bruijn sequence, we get a sequence with length 2n-1 which is called span n sequence. The linear complexity of an n-stage de Bruijn sequence is between 2n-1+n and 2n-1, but the linear complexity of corresponding span n sequence could drop to n. Because of this, the linear complexity of span n sequence becomes an important property in measuring the quality of de Bruijn sequence, so it is very meaningful to study how to generate span n sequence with high linear complexity. In this article we study the method of searching span n sequence based on special function and non-linear feedback shift register proposed in literature [6], and find that the independency between span n sequence and parameter t, on this basis we propose some improved methods. We also make the horizontal comparison on various algorithms, and point out their pros and cons and the possible improvement in the future. Non-linear feedback shift registerde Brujin sequenceSpan n sequence 2015-09-07。屈哲,硕士,主研领域:伪随机序列。陈克非,教授。 TP3 A 10.3969/j.issn.1000-386x.2016.10.069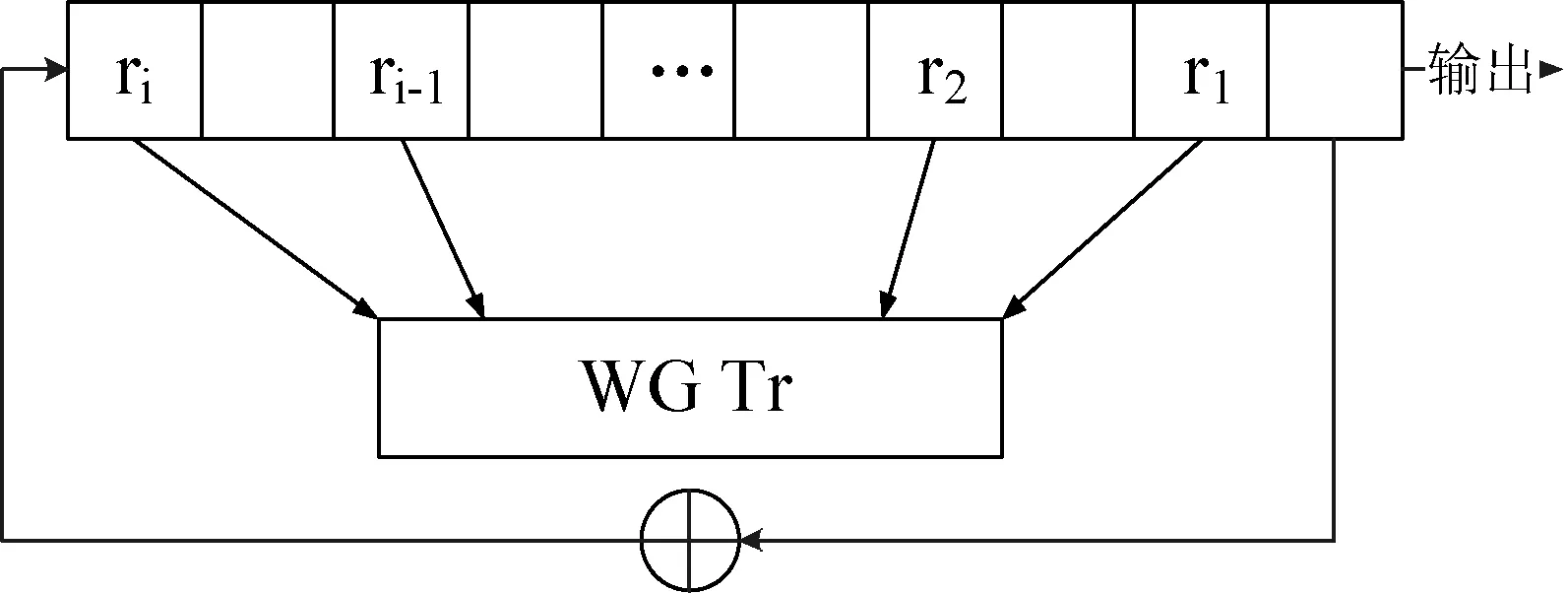
2 寻找span n序列的几种算法

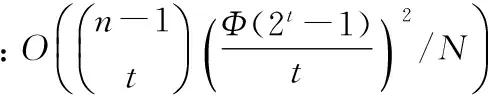


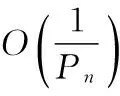
3 实验结果与相关分析








4 结 语
