基于增量信息索引的子图查询算法

王超珲　黄一夫

(复旦大学计算机科学技术学院智能信息处理重点实验室　上海 200433)



基于增量信息索引的子图查询算法

王超珲黄一夫

(复旦大学计算机科学技术学院智能信息处理重点实验室上海 200433)

当前图数据库中的子图同构查询算法主要是依赖倒排索引，然而处理那些具有庞大数据的数据库和复杂的查询愈发成为挑战。研究目的是设计一个算法，使用新的索引作为查询处理的核心，记录查询图的每一个细小改变，并使用一种特殊的数据结构来维护。先是引出一个索引算法，然后逐渐分析整个索引、查询过程，并利用该算法实现一个系统，最后在不同数据集和查询上进行实验。实验证明了该算法具有良好的时间、空间效率和扩展性。新的索引算法能够支持更大的查询图和更加灵活的查询。通过实现的系统和其他系统的对比实验，验证了算法的有效性。

图数据库子图同构片段子图查询索引查询算法

0　引　言

随着互联网步入2.0时代，图数据库越来越多地出现在我们的生活中，例如社交网络、蛋白质网络、化学结构等，对于它的检索需求也与日俱增。你可以在Facebook查看你好友或者好友的好友发出的消息；你可以在生物信息数据库中研究某种DNA、某种氨基酸、某种蛋白质；你可以在化学数据库中查询某种化学结构。支撑这些应用的底层存储数据库不是普通的数据库，而是图数据库。当你使用这些应用时会有图数据库查询，即使你没有意识到，这一切都在不知不觉中进行着。

有的图数据库本身就是一张大图[1]，有的图数据库中存储了千千万万的小图。传统的数据库只能将一个图存为一个整体，不能利用其中的结构信息。随着技术的进步和发展，图数据库的实用价值不断增大，所以使用的比例也不断加大。

图数据库需要检索技术，本文研究的检索是子图同构检索。进行这样的检索有几个要求：检索结果需要完全正确，不能漏掉数据库中应该检索到的图，或者检索出不正确的图；检索处理的速度需要足够快，同时使用的内存要合理。

顺序枚举数据库里的每个图，并且查看查询是不是它的子图是效率比较低的做法。因为子图同构查询是NP完全问题[2]，在整个图数据库上进行，花费很大。因此，现在通行的做法是建立索引，之后在查询时进行两阶段的处理：过滤和验证。过滤是在图数据库中选出部分图组成候选集集合，过滤掉一些不符合的图，缩小需要运行子图同构检测的数据范围大小。这时，候选集已经大大减小了，需要运行子图同构检测的次数变少了，可以加快查询的速度。验证部分运行子图同构检测，确定正确的结果。如果过滤步骤能够显著地降低候选集的大小，那么这个基于索引的两阶段算法就是有效并且实用的。候选集的大小可以作为不同算法性能直接比较的一个重要指标。

GraphGrep[3]提出了子图查询问题，Tree+Δ[4]使用了树作为索引，gIndex[5]使用了图作为索引，FG-Index[6]提出了避免过滤阶段的方法。传统的索引是建立频繁子图的倒排索引，没有利用其中的结构信息。本文在构建索引时在子图之间增加信息，构建的索引是由子图构成的图。

本文研究的主要目的是设计一个符合以上要求的支持子图查询的算法。

1　基本概念

1.1相关定义

定义2图G1子图同构于图G2(表示为G1⊆G2)，若存在一个单射函数f:V1→V2，使得∀u∈V1都有φ1(u)=φ2(f(u))；∀(u,v)∈E1都有(f(u),f(v))∈E2。

定义3一个图G的正规表示Canon(G)是一个带标签的图，同构于G，且任意同构于G的图都和G有相同的正规表示，正规表示是唯一的。找寻图的正规表示的问题叫作图的正规化。因此，如果有一个图的正规化的算法，这个算法同样能够解决图的同构问题。对于两个图G和H，计算它们的正规表示Canon(G)和Canon(H)，然后检测两个正规表示是否相同。如果相同必定同构，如果不同必定不同构[7]。

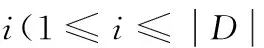
定义5术语片段用于称呼图数据库或者查询图中的一个小的子图。

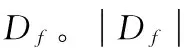
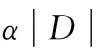
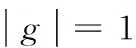
1.2问题描述

本文研究的图数据库，是由许多的小图组成的。每个小图的规模都不大(点数、边数<200)，但是小图的数目非常多(10×103～200×103)。给定图数据库D={G1,G2,…,Gn}，查询图Q。子图查询问题是找出所有的Gi，使得Q⊆Gi。

2　算　法

传统的索引是建立频繁子图的倒排索引，没有利用其中的结构信息。并且传统的索引没有考虑到索引本身和查询之间的联系。本文在构建索引时在子图之间增加信息，构建的索引是由子图构成的图。这是为了查询时使用的特性而特别优化的。

图1是整体系统的结构，包含有索引构建器、查询处理机和验证器。索引构建器能够输入图数据库并且为其构建索引。查询处理器用于处理查询，输入查询后对查询进行分析，在读取索引的同时维护一个数据结构保存图的特征信息。这些信息是同时和查询图和索引相关联的，从这个数据结构中可以提取候选集，传递给验证器。验证器用于验证候选集，输出查询结果。

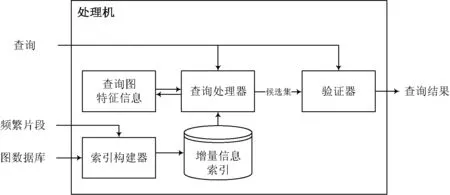
图1　系统结构图

2.1增量信息索引

本文提出的增量信息索引结构本身是一个分层的有向无环图，图2是从本文使用的索引所进行的可视化展示中截取的。

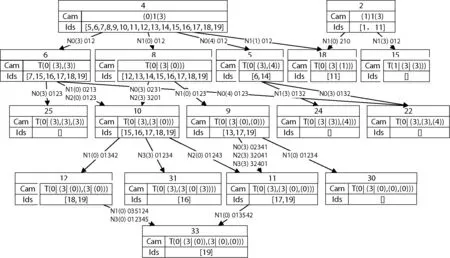
图2　增量信息索引结构图

定义9若有图数据库D和其上的频繁片段集合F，可以构建增量信息索引I={I1,I2,…,In}。索引中的每一项Ii都对应一个片段，由标识符、正规编码、类型、大小、转移信息、父亲和支持图集合组成。

这里我们只将频繁片段和显著非频繁片段放入增量信息索引中，这样做的原因是所有片段的种类是非常多的，不可能全部放入索引中。已知使用频繁片段是一种能大幅度降低片段数量的方法，可以通过调节最小支持度阈值α来控制数量，并且过滤效果很好。本文使用一种已有的图数据库挖掘算法gSpan生成频繁片段[9]。

片段的转移信息是一个数组，表示片段上所有可以进行的操作和操作的结果。操作就是给片段增加一条边，因为增加完边后片段仍旧是连通的，所以操作有两种：

(1) 增加边的同时增加一个新的结点，新的边将新的结点连接到片段中一个已有的结点上，我们记这种操作为Nx(y)。其中x为已有结点的编号，y为新结点的标签。如N0(C)表示将一个标签为C的新结点连接到已有的0号结点上。

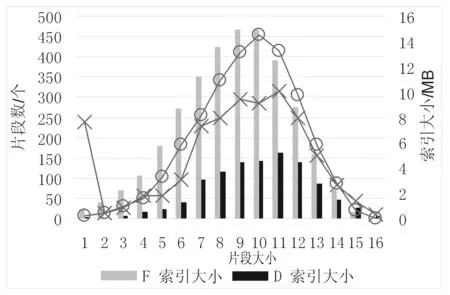
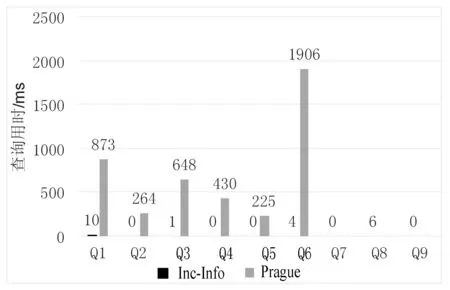
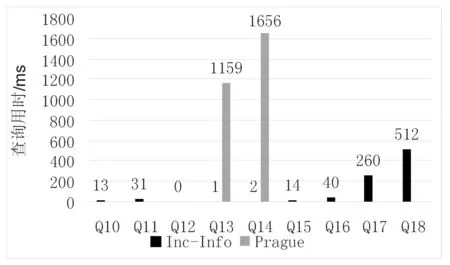
(2) 在已有的两个没有边连接的结点之间连接一条边，我们记这种操作为Cx-y。其中x、y分别为已有两个结点的编号，且x

定义10操作的结果叫作转移(trans)，形如 (id,newIds)。若这个操作是对片段a做的，得到片段a′，a′的正规表示为b，那么id为b的标识符，newIds表示的是a′到b的同构映射函数f。

2.2增量信息索引的构建

首先，将所有频繁片段连同它们的信息(包括它们的支持图集合)放入增量信息索引中。然后依次枚举所有的频繁片段，并对其尝试前文所提到的两种操作：增加边的同时增加一个新的结点，在已有的两个没有边连接的结点之间连接一条边。若操作的结果从片段f得到新图newGraph和转移newIds，片段f在索引中对应的项为If。根据newGraph的性质进行以下操作：

1) 若newGraph是频繁片段，对应索引中的项InewGraph，我们记录三元组(op,InewGraph.id,newIds)到索引中If项的信息中。

3) 若newGraph是显著非频繁片段，对应索引中的项InewGraph，我们记录三元组(op,InewGraph.id,newIds)到索引中If项的信息中。

4) 若newGraph是非显著非频繁片段，我们不做任何事。

最后检查所有的DIF，若其支持图集合为空，则其支持图集合的候选集C可由它所有父节点支持图集合的交集得到。在C上运行验证器可以得到其支持图集合。

2.3简单纺锤形图

在文献[10]中，作者提出了纺锤形图的概念。本文在此基础上提出了简单纺锤形图，作为查询图的特性信息。简单纺锤形图改变了图中每个结点所代表的意义和包含的信息，不过还是继承了其纺锤形的特征和思想。文献[10]中使用多个纺锤形图，本文只使用一个简单纺锤形图；原有纺锤形图每个结点都是原有查询中的一个片段，本文只是索引项的标识符；原有纺锤形图中结点的总个数一定是查询图所有连通子图的个数，本文简单纺锤形图中结点数量的增长较为平缓。因此本文缩减了操作简单纺锤形图的时间，使得添加边、删除边的操作更加高效。

定义11简单纺锤形图(SimpleSPIG)是一个图，结点i带有数据{id,edgeSets}。i.id是增量信息索引中索引项的标识符。若两个简单纺锤形图中的结点各自对应的索引项在增量信息索引中有边连接，那么在简单纺锤形图中这两个结点也有边连接。i.edgeSets是边集的集合且不为空。

图3展示了简单纺锤形图的结构。当用户插入了一条边后，简单纺锤形图只会增加结点和结点中的边集。当用户删除边后，简单纺锤形图中的结点和结点中的边集只会减少。我们需要实现增加边和删除边的算法。

图3　简单纺锤形图

2.4增加查询边算法

每次加入新的边时，会更新简单纺锤形图。用广度优先搜索从小到大找出所有包含种子边的查询图的连通子图。广度优先搜索所使用的队列里存储的是用于表示片段的三元组(查询结点标识符数组,边集,索引项的标识符)。其中查询结点标识符数组和边集可以定位片段在查询图中的位置，索引项的标识符可以定位片段在索引中的位置。

每次从队列中取出一个三元组后，我们尝试所有给它加边的方法，加上新的边得到新的边集。若还没有被处理过，使用加边操作在索引信息中查找。若能找到对应的转移，利用查询结点标识符数组和转移中的newIds构建新的查询结点标识符数组，并且将新的三元组加入到队列中去。并且，同时将标识符添加到简单纺锤形图中，这里添加时需要使用父亲信息。这是因为若有父亲已经存在在简单纺锤形图中，我们需要连一条到父亲的边。然后将边集加入到简单纺锤形图结点的边集中。

等到队列全部处理完成的时候，算法也就终止了，此时更新也完成了。

2.5删除查询边算法

删除一条边的算法只需要对简单纺锤形图进行更新就可以了，不需要使用到索引的信息。其主要的思想是移除所有简单纺锤形图中包含有需要删除边的边集，若移除后简单纺锤形图中结点的边集集合为空，说明此结点的限制不必再应用于这个查询，可以移除这个结点了。更新完成后就可以得到所需的新的简单纺锤形图。

2.6得到查询结果

这里需要根据简单纺锤形图的层数分两种情况：

1) 若层数存在和查询大小相同的这一层，简单纺锤形图形成一个完整的纺锤形，那么说明查询本身就在索引中出现过。可以直接使用索引的支持图集合作为查询的结果，不需要再做验证。

2) 否则，还需要再次通过验证器验证才能作为查询的结果。先从简单纺锤形图中所有叶子结点中取出它们的支持图集合，并把这些集合的交集作为查询结果的候选集，验证完后作为查询结果。只取所有的叶子结点是因为，若一个结点不是叶子结点，那么它一定有一个后代并且这个后代的支持图集合是它的支持图集合的子集，所以没有必要再和非叶子结点的支持图集合做交集操作。

3　实验结果与分析

本文所实现的程序称为Inc-Info，将与之前的算法Prague进行比较，并进行性能测试。实验是在一台IntelCorei7-4700MQ处理器、12GB内存、运行Windows8.1x64操作系统的计算机上进行的。实验环境上安装有Java1.8和Graphviz2.38。

实验的数据集是AIDS抗病毒数据集，是一个真实的数据集，总共包含有43 000个化学结构。取频率阈值α为0.1，并运行gSpan生成频繁片段。

图4显示了在AIDS数据集上建立索引，得到片段数与索引大小、片段大小的关系。频繁片段的总数为2847，构建时间为70分钟，总索引大小为139.3MB，其中支持图集合占138.5MB，数据库文件占用磁盘总空间237MB。实验表明，片段个数会随着片段大小的增长而增多，但是达到一个最大值后反而会下降，最后归零，说明此算法片段数是可控的。在最后得到的增量信息索引中，支持图集合占据了绝大部分空间，说明本算法表示索引结构部分的信息是十分高效的。

图4　索引大小分布图

本文手工构建了18个查询图，作为测试样例。在Inc-Info和Prague上输入测试Q1-Q18，得到查询用时，见图5、图6所示。其中Q7-Q12、Q15-Q18的图比较大，Prague无法处理，因此没有结果。可以发现Inc-Info的查询用时较小。

图5　Q1-Q9测试用时

图6　Q10-Q18测试用时

表1是在Inc-Info和Prague上输入Q1后，删除一条边所获得的操作用时。Prague不支持删除边5-边7的操作，因为Prague不能留下不连通的查询图，这点上Inc-Info较为灵活。而且可以看到Inc-Info较Prague在时间效率上有优势。

表1　删除边测试结果

4　结　语

本文提出了能够快速转移的新索引结构、一种新的查询时数据结构简单纺锤形图，组成一种新的相似度查询过滤算法。这种新算法可以支持更大的查询图，并有更高的查询性能。通过实验，将本文系统和现有系统进行比较，证明了本文提供的算法在实践上也具有良好的表现。未来可能的研究方向将关注如何缩小增量信息索引的大小，加快索引构建速度。

[1]SunZ,WangHZ,WangHX,etal.Efficientsubgraphmatchingonbillionnodegraphs[J].ProceedingsoftheVLDBEndowment,2012,5(9):788-799.

[2]GareyMR,JohnsonDS.Computersandintractability:aguidetothetheoryofNP-completeness[M].USA:W.H.FreemanandCompany,1979.

[3]GiugnoR,ShashaD.GraphGrep:afastanduniversalmethodforqueryinggraphs[C]//Proceedingsofthe16thInternationalConferenceonPatternRecognition,Quebec,Canada,2002,2:112-115.

[4]ZhaoPX,YuJX,YuPS.Graphindexing:tree+delta>=graph[C]//Proceedingsofthe33rdInternationalConferenceonVeryLargeDataBases,2007:938-949.

[5]YanXF,YuPS,HanJW.Graphindexing:afrequentstructure-basedapproach[C]//Proceedingsofthe2004ACMSIGMODInternationalConferenceonManagementofData,2004:335-346.

[6]ChengJ,KeYP,NgW,etal.FG-Index:towardsverification-freequeryprocessingongraphdatabases[C]//Proceedingsofthe2007ACMSIGMODInternationalConferenceonManagementofData,2007:857-872.

[7]Canonicalform[EB/OL].Wikipedia[2015-03-20].http://en.wikipedia.org/wiki/Canonical_form.

[8]JinC,BhowmickSS,XiaoXK,etal.GBLENDER:towardsblendingvisualqueryformulationandqueryprocessingingraphdatabases[C]//Proceedingsofthe2010ACMSIGMODInternationalConferenceonManagementofData,2010:111-122.

[9]YanXF,HanJW.gSpan:graph-basedsubstructurepatternmining[C]//Proceedingsofthe2002IEEEInternationalConferenceonDataMining,2002:721-724.

[10]JinCJ,BhowmickSS,ChoiB,etal.Prague:towardsblendingpracticalvisualsubgraphqueryformulationandqueryprocessing[C]//Proceedingsofthe2012IEEE28thInternationalConferenceonDataEngineering,2012:222-233.

ASUBGRAPHQUERYALGORITHMBASEDONINCREMENTALINFORMATIONINDEX

WangChaohuiHuangYifu

(KeyLabofIntelligentInformationProcessing,SchoolofComputerScience,FudanUniversity,Shanghai200433,China)

Currentlysubgraphisomorphicqueryalgorithmsingraphdatabasemainlydependoninvertedindex.However,theprocessingofthosegraphdatabaseswithhugedataandthecomplicatedqueriesincreasinglybecomesachallenge.Thepurposeofourresearchistodesignanalgorithm,weusedanewindexasthecoreofqueryprocessing,recordedeverytinychangeinquerygraph,andmaintaineditwithaspecialdatastructure.Firstweintroducedanindexalgorithm,andthengraduallyanalysedthewholeprocessofindexandquery,andusedthealgorithmtohaveimplementedasystem,finallywecarriedouttheexperimentsondifferentdatasetsandqueries.Thisalgorithmhasbeenprovedwithgoodtimeandspaceproductivityandscalability.Thenewindexalgorithmisabletosupportgreaterquerygraphandmoreflexiblequery.Throughtheimplementedcomparativeexperimentsbetweenthissystemandothersystems,weverifiedtheefficiencyofthisalgorithm.

GraphdatabaseSubgraphisomorphismFragmentSubgraphqueryIndexQueryalgorithm

2015-05-18。王超珲，硕士生，主研领域：数据库。黄一夫，硕士生。

TP

ADOI:10.3969/j.issn.1000-386x.2016.10.009