组合Baarda数据探测法与ESD检验法探测伪距粗差的新方法

林国钻,邱斌

(中南大学 地球科学与信息物理学院,长沙 410083)



组合Baarda数据探测法与ESD检验法探测伪距粗差的新方法

林国钻,邱斌

(中南大学 地球科学与信息物理学院,长沙 410083)

在采用GNSS技术进行卫星导航定位过程中,伪距观测值粗差会污染定位观测模型,造成定位精度下降。 本文提出了一种融合Baarda数据探测法和ESD检验法两种方法进行组合探测伪距观测值粗差的新方法,实验证明，该方法可以有效控制伪距粗差的影响,保障伪距单点定位的精度和可靠性。

GNSS;伪距粗差;Baarda数据探测法;ESD检验法

0　引　言

伪距单点定位较之载波相位定位精度较低,但是由于其定位模型简单,实施容易,已广泛应用于卫星导航定位领域中。一般情况下,伪距定位的精度主要依赖于伪距观测值噪声水平以及卫星信号传播过程中涉及的各项误差、如卫星星历误差、卫星钟差、大气延迟、多路径效应等,其定位精度根据不同的接收机、观测环境和误差消除水平从米级到数十米不等。然而在实际定位中,特别是动态定位过程中,伪距观测值可能存在粗差,粗差观测值会污染整个定位模型,降低卫星定位的精度,有时甚至严重偏离其真实位置,因此有必要对伪距观测值进行粗差探测,保障定位精度的可靠性。

伪距粗差探测常用的方法有卡尔曼滤波法和完备性监测法[1]。卡尔曼滤波法需要设计合适的滤波器,如果接收机载体运动机动性比较强,可能导致滤波发射引起误判。完备性监测法通过逐次剔除卫星达到满足方差检验的要求,其过程类似于多维粗差同时探测法[2],而多维粗差同时探测法与Baarda数据探测法具有等价性[3]。这类粗差剔除方法在多余观测数较少或者可靠性矩阵列向量强相关时,容易造成粗差的误探或漏探[4]。本文拟引入ESD检测法[5]来提高已有方法粗差探测的能力。

1　基于Baarda数据探测法探测伪距粗差

伪距定位的基本观测方程为[6]

Rk=ρk+c·(δtk-δtr)+δion+δtrop+

δmul+εR,

(1)

式中: 上标k表示卫星; R表示伪距观测值; ρ为卫星到接收机的几何距离; c为光速; δtr和δtk依次表示接收机和卫星的钟差; δion、δtrop依次表示电离层延迟和对流层延迟; δmul表示伪距观测值的多路径效应,εR表示伪距的观测噪声．在实际伪距单点定位过程中,需要将式(1)进行线性化：

ρk,0+δion+δtrop+δmul+εR,

(2)

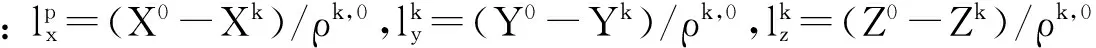
在实际定位计算中,卫星钟差由广播星历计算得到,电离层延迟和对流程延迟可用模型改正,多路径效应由于难以模型化,一般将其当作随机误差进行处理。记V为残差向量,A为设计矩阵,X为参数向量,L为“观测值-计算值”向量,P为权阵,一般基于高度角定权给出[7]。那么,线性化后的伪距观测方程组为

V=L-A·X,

(3)

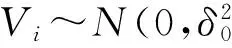
(4)

(5)

式中： QVV=P-1-A(ATPA)-1AT；δ表示单位权中误差； Qvivi表示残差斜因数阵Qvv对角线上的第i个元素。

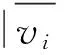
2　基于ESD检验法探测伪距粗差

Baarda数据探测法可以高效探测出伪距观测中的粗差,但是其探测能力依赖于“干净”的多余观测值数量以及卫星的几何结构,当多余观测数较少时或者观测值方程的可靠性矩阵列向量强相关时,存在粗差漏探和错探的风险[4]。为了降低上述风险出现的概率,补充ESD检验法对伪距观测值进行粗差探测。ESD检验法的关键在于构造服从正态分布的统计量,现以载波与伪距的差值构造ESD检验量T

T=λφ-R=λN-2δion+εφ-εR.

(6)

由上式可知,检验量T主要由三部分组成,模糊度参数N、电离层延迟δion和伪距观测噪声εR(载波观测噪声εφ远低于其他三部分,可以忽略)。在短时间内,电离层延迟变化比较平稳,而模糊度N只要载波观测值无周跳时则为常数,所以可认为T近似符合正态分布,可开窗对T序列进行粗差探测:

(7)

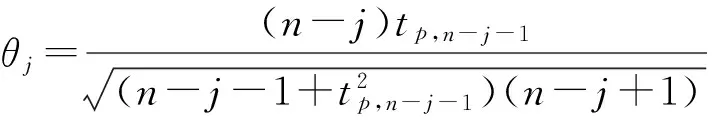
j=1,2,…,r,

(8)

(9)

式中:n为T序列的元素个数;α为置信度,一般取0.05,下标j表示迭代次数,Tj表示第j次迭代序列T剩余元素组成的序列; (Tj)mean表示序列Tj的平均值,|Tj-(Tj)mean|max为序列Tj与其均值偏差最大值,si为序列Tj的std值;tp,n-j-1为t分布概率P,自由度为n-j-1对应的上侧分位数。如果检验量ej≤θj则认为Tj序列是干净的,不含有粗差,考虑GNSS伪距单点定位的特点,可将粗差认定条件设置为

(10)

即序列Tj中元素与其均值的最大偏差值要大于5 m才可认定为粗差。基于上述ESD检验法,可以对满足窗口长度的卫星进行伪距粗差探测。当窗口长度不够,即样本数太小时,ESD检验法探测粗差的效果将受影响。当然为了避免载波大周跳对本方法的影响,有必要对周跳进行探测,本文采用高次差法进行周跳探测[9]。

现将两种方法结合使用来探测伪距粗差,其具体过程为：先采用ESD检验法逐个卫星对当前历元的伪距观测值进行粗差探测,如果卫星伪距观测值序列满足窗口长度则进入ESD检验法,如果ESD检验法探测当前历元存在粗差则对卫星进行粗差标记,否则认为不存在粗差;然后在Baarda数据探测法中对ESD探测法已经标记有粗差的卫星观测值预先剔除,对剩余观测量进行粗差探测。

3　实验分析

算例1:采用一段某滑坡监测GPS单频接收机3h的观测数据进行实验,卫星截止高度角为10°,数据采样间隔为15s,观测卫星数及PDOP值如图1所示。为了分析本文提出的新方法在伪距粗差探测中的有效性,对某些历元伪距观测值数据添加粗差,如表1所示,设计4种计算方案对数据进行解算,分别为,方案1:最小二乘法;方案2:Baarda数据探测法;方案3:先用ESD检验法探测伪距粗差,然后采用最小二乘法进行单点定位;方案4:新方法,即先用ESD检验法探测伪距粗差,然后再用Baarda数据探测法进行单点定位。

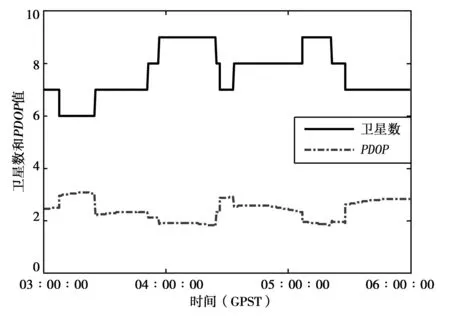
图1　观测卫星数及PDOP值

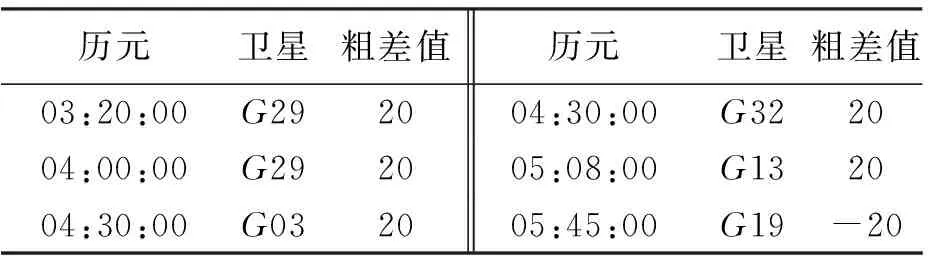
历元卫星粗差值历元卫星粗差值03:20:00G292004:30:00G322004:00:00G292005:08:00G132004:30:00G032005:45:00G19-20

图2所示为分别采用4种方案单点定位结果与真值的点位偏差图。直接采用最小二乘法的方案1受模拟添加粗差的影响,添加粗差的对应的5个历元的点位偏差较大(圆圈所示),而采用数据探测法的方案2较之方案1点位偏差较大点仅仅出现在历元04:30:00(正形所示),说明数据探测法对其他4个历元的粗差都可以准确探测到。分析历元04:30:00探测失败的原因在于该历元的卫星观测数为7,而模拟添加了2个粗差,即有效观测数据只有5个,而必要估计参数有4个,即多余观测数只有1个,这种情况下数据探测法容易出现错探和漏探,这也是该历元的点位偏差方案2较之方案1更大的原因。采用ESD检验法探测粗差的方案3较之方案1,也仅有历元05:08:00出现了大偏差(圆点所示),ESD检验法未能探测出该历元G13卫星模拟加入的伪距粗差。分析原因在于G13在历元05:07:00开始出现,历元05:08:00其数据样本数还未达到ESD检验法所需要的窗口长度,即该历元无法采用ESD检验法对G13卫星伪距观测值进行粗差探测。组合两种粗差探测方法的方案4消除了点位偏差的所有跳点,即新方法对模拟加入的粗差进行了有效探测。

算例2:采用城市道路测量的GPS/BDS双模动态数据进行实验,数据采样间隔为1s,观测卫星数及PDOP值如图3所示。为了分析本文提出的新方法在动态数据中的有效性,对某些历元伪距观测值数据添加粗差,如表2所示,分别采用最小二乘法和新方法对数据进行解算。

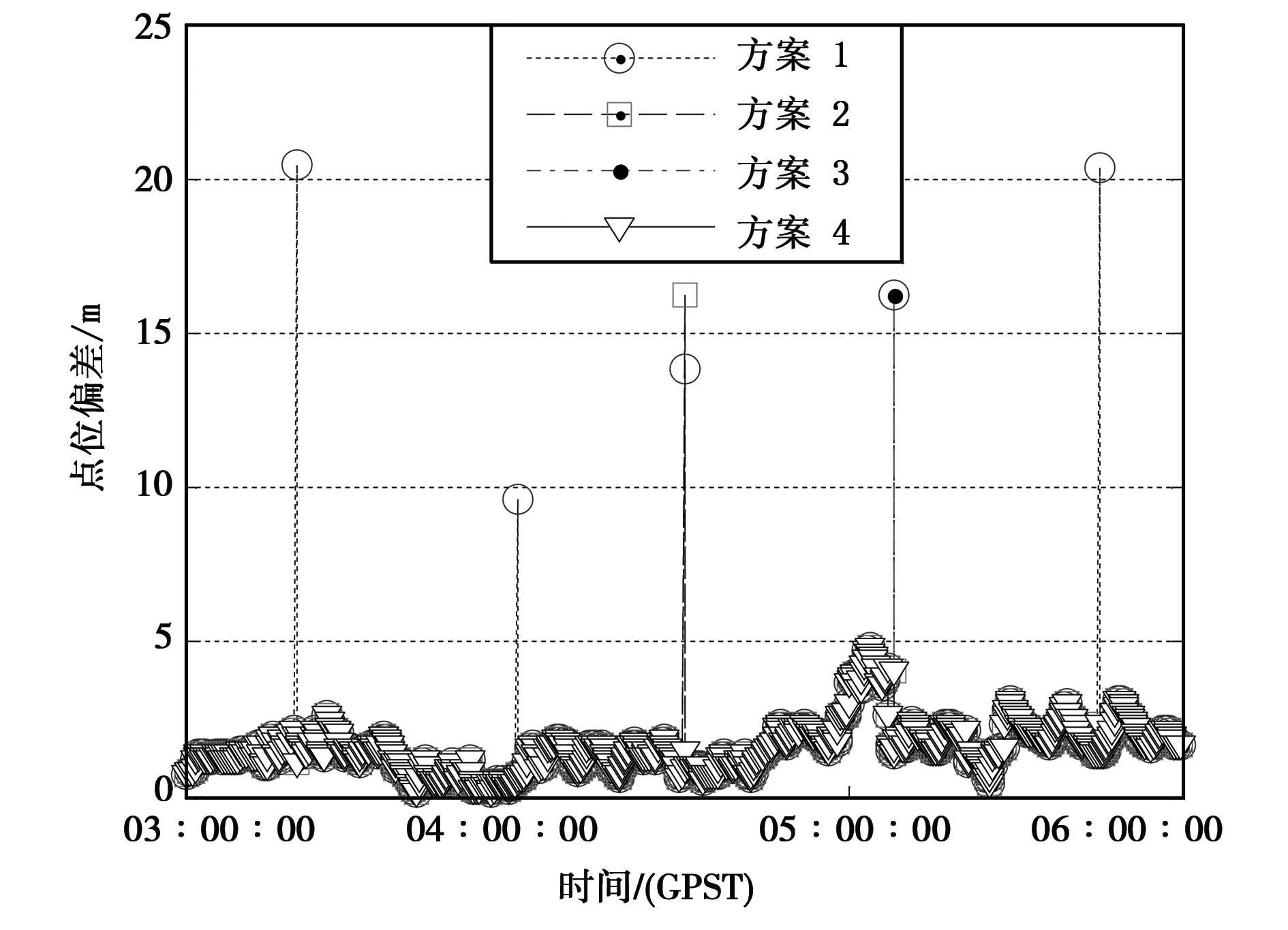
图2　点位偏差

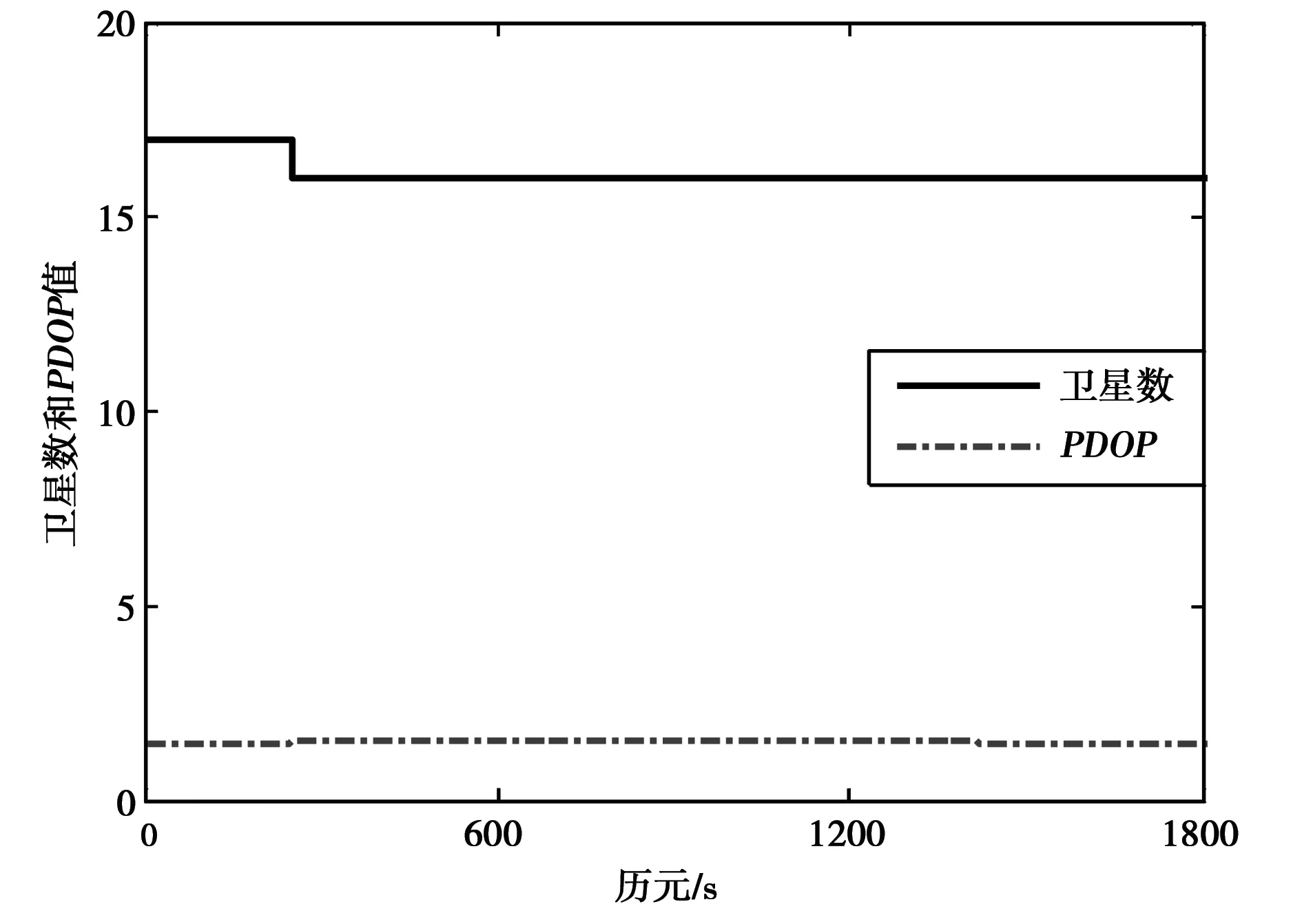
图3　观测卫星数及PDOP值

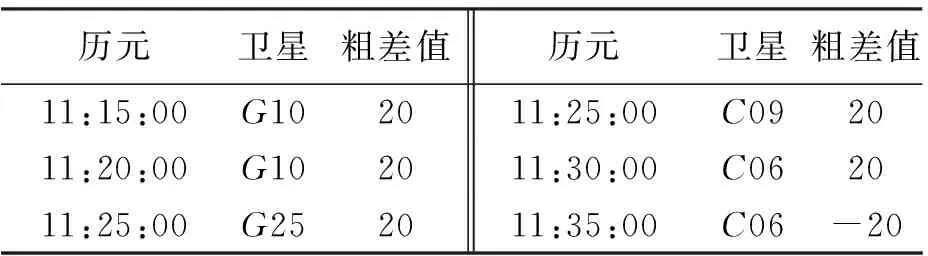
历元卫星粗差值历元卫星粗差值11:15:00G102011:25:00C092011:20:00G102011:30:00C062011:25:00G252011:35:00C06-20

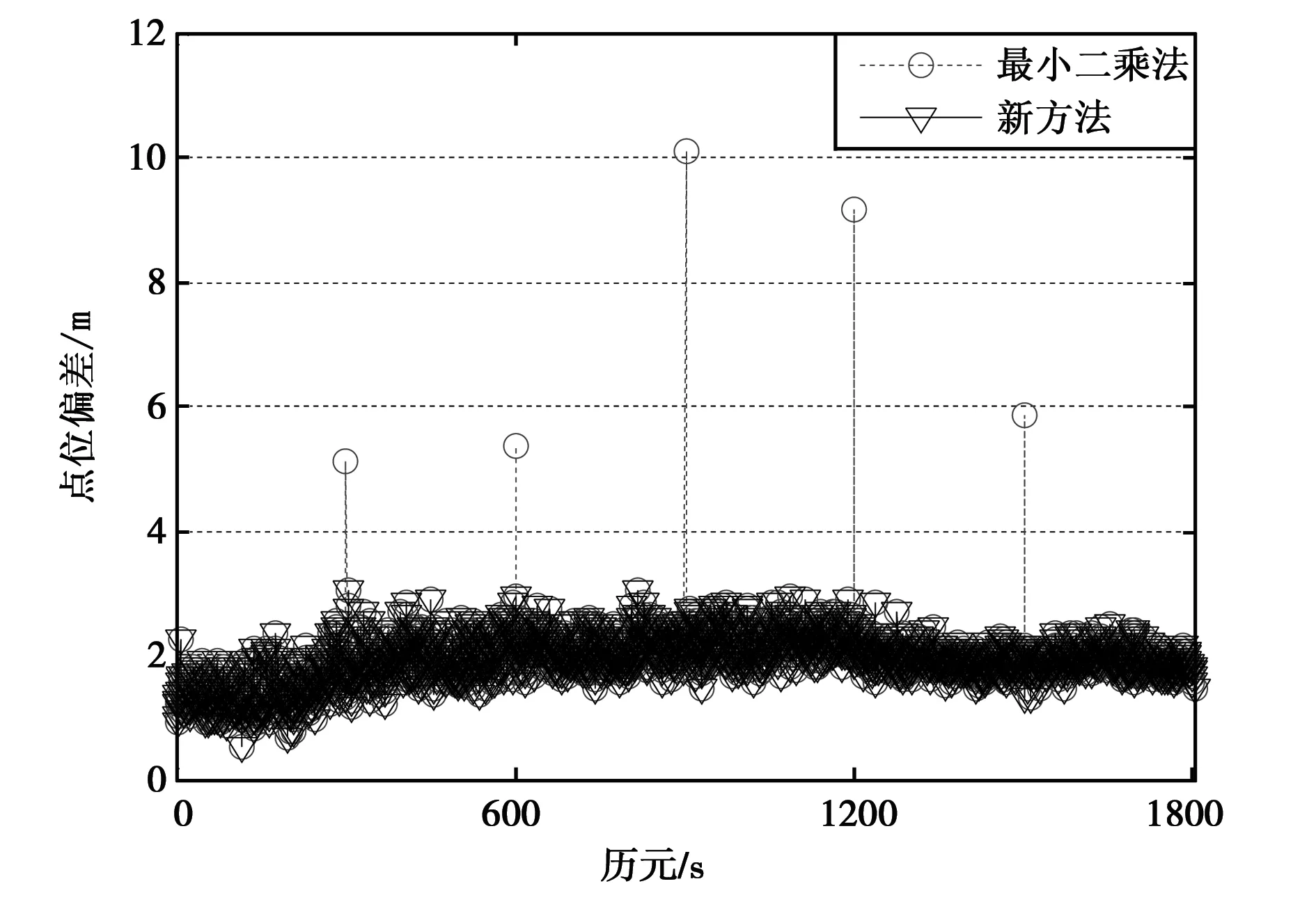
图4　点位偏差

由图4可知,直接采用最小二乘法进行单点定位,在模拟添加伪距粗差的5个历元点位偏差出现了跳点。由于GPS/BDS双模观测卫星数比较多,相同量级的伪距粗差对算法2的影响较之算例1要低。新方法对模拟加入的伪距粗差进行了有效探测,5个历元的定位结果恢复正常。

4　结束语

在GNSS实际作业中,伪距观测值可能出现粗差,粗差会造成定位精度的下降,有时甚至严重偏离真值,因此有必要对伪距观测值中的粗差进行探测并处理。本文提出的利用ESD检验法和Baarda数据探测法两种方法组合探测粗差的方法,分别从卫星观测值时间序列和单个历元定位模型解算两个角度进行粗差探测,可有效提高伪距粗差探测的准确性,降低伪距粗差导致定位精度下降的概率。

[1]秘金钟,李玮,谷守周. 精密单点定位用户自主式完备性监测算法[J].测绘学报,2011,40(5):63-65.

[2]於宗俦,李明峰. 多维粗差的同时定位与定值[J]. 武汉测绘科技大学学报,1996,21(4):17-23.

[3]宋力杰,杨元喜. 均值漂移模型粗差探测法与LEGE法的比较[J]. 测绘学报,1999,28(4):295-300.

[4]陶本藻,姚宜斌,施闯. 基于相关分析的粗差可区分性[J]. 武汉大学学报(信息科学版),2004,29(10):881-884.

[5]ROSNERB.PercentagepointsforageneralizedESDmany-outlierprocedure[J].Technometrics, 1983, 25(2): 165-172.

[6]XUG.GPS:theory,algorithmsandapplications[M].SpringerScience&BusinessMedia, 2007.

[7]郭秋英.GPS快速精密定位数据处理[M].徐州:中国矿业大学出版社,2011:69-71.

[8]TIBERIUSCJM,BORREK.AreGPSdatanormallydistributed[M].GeodesyBeyond2000,SpringerBerlinHeidelberg, 2000: 243-248.

[9]严新生,王一强,白征东，等. 联合使用高次差法和TurboEdit法自动探测、修复周跳[J].测绘通报,2007(9): 5-8.

A New Method Which Combines Baarda Data Snooping and the ESD Test to Detect Pseudorange Observation Outlier

LIN Guozuan,QIU Bin

(SchoolofearthscienceandinformationPhysics,CentralSouthUnivercity,Changsha410083,China)

In the process of navigation positioning with GNSS technology, the observation model would be polluted by the pseudorange observation outlier, which causing the deterioration of positioning accuracy. To solve this problem, a new method to detect pseudorange observation outlier, combined Baarda data snooping method and the ESD test, was proposed in this paper. Experiments showed that, with the new method, the influence of pseudorange observation outlier can be controlled, and the precision and reliability of positioning service can be guaranteed.

GNSS; pseudorange outlier; Baarda data snooping; ESD test

10.13442/j.gnss.1008-9268.2016.04.013

2016-04-07

P228.4

A

1008-9268(2016)04-0059-04

林国钻(1989-),男,福建龙岩人,硕士生,主要研究GNSS数据处理、大地水准面精化。

邱斌(1968-),男,湖南衡阳人,高级工程师，主要从事变形监测及测量数据处理、GPS理论与应用、大地水准面精化等方面的研究与教学工作。

联系人： 林国钻 E-mail: linguozuan@163.com