双线性变换法在IIR滤波器设计中的应用

张登奇， 彭 鑫， 陈海兰

（湖南理工学院 信息与通信工程学院， 湖南 岳阳 414006）

双线性变换法在IIR滤波器设计中的应用

张登奇， 彭 鑫， 陈海兰

（湖南理工学院 信息与通信工程学院， 湖南 岳阳 414006）

数字滤波器的设计是数字信号处理课程的重要教学内容， 而双线性变换法是间接设计IIR数字滤波器的重要方法. 本文介绍了双线性变换法的设计原理， 并以巴特沃斯数字低通滤波器为例， 归纳了双线性变换法的设计步骤， 对设计过程中较难理解的过渡滤波器和频率预畸变进行了分析， 对变换常数和采样周期的取值问题进行了讨论， 并以实例给出了MATLAB实现的程序.

数字滤波器； 双线性变换法； 预畸变； MATLAB

引言

间接设计IIR数字滤波器的常用方法有脉冲响应不变法和双线性变换法. 文［1］对脉冲响应不变法进行了介绍和分析， 但由于存在频谱混叠失真， 故不适合设计高通和带阻滤波器. 双线性变换法通过频率的非线性变换， 解决了频谱混叠问题， 得到了广泛应用. 但一般教材对其原理论述简单， 对某些参数介绍不详， 导致学习理解困难. 本文从脉冲响应不变法的频谱混叠入手， 先分析双线性变换法的原理思想， 再以巴特沃斯数字低通滤波器的设计为例， 归纳双线性变换法的设计步骤， 并对设计过程中较难理解的过渡滤波器和频率预畸变进行深入分析， 最后以实例给出MATLAB的实现程序.

1　双线性变换法

1.1设计原理

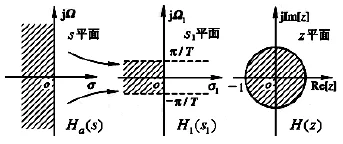
图1　双线性变换过程示意图

其中C是一个正实常数， 也称变换常数. 由于

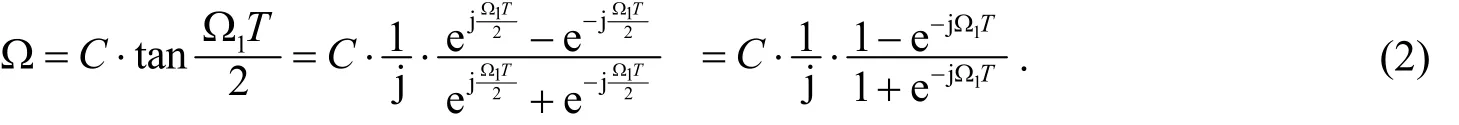
再将s1平面通过映射到z平面， 得

1.2设计步骤

双线性变换法可由（5）式直接将）（sHa变换成）（zH，但设计）（sHa的技术指标并不好理解.下面以巴特沃斯低通滤波器的设计为例， 结合图2所示设计指标及幅频特性的变化过程， 介绍双线性变换法的设计步骤， 并对设计指标进行分析说明.

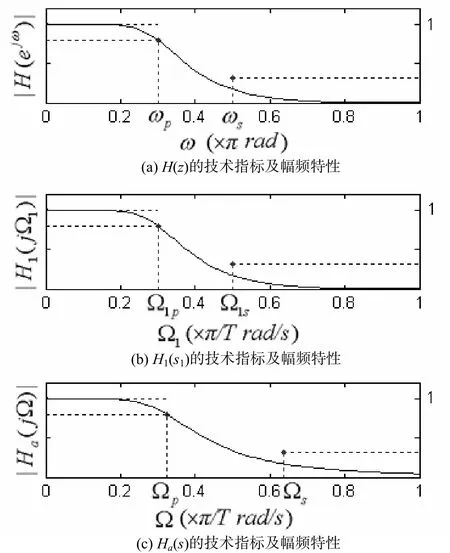
图2　设计指标及幅频特性的变化过程

实例 对输入的模拟信号进行采样得离散时间信号，设采样频率Fs=20kHz， 要求保留3000Hz以下的频率成分，幅度失真小于2dB； 滤除5000Hz以上的频率成分， 衰减大于10dB. 试用双线性变换法设计数字滤波器实现上述要求.

（1） 确定采用巴特沃斯数字低通滤波器.数字指标为ωp=0.3π rad ，ap=2dB （即0.7943倍）， ωs=0.5π rad，as=10dB （即0.3162倍）. 在用双线性变换法设计数字滤波器的公式中， 幅度指标要以分贝为单位代入数据， 但用分贝为单位图示的幅频曲线感觉衰减不明显. 故在图2（a）点状图所示的幅频指标中， 幅度指标数据的单位改用倍数.

（2） 将数字低通滤波器的技术指标转换成虚构的过渡模拟滤波器技术指标. （5）式描述了s平面与z平面的映射关系， 令s=jΩ， z=ejω， 代入（5）式可得过渡模拟角频率与数字频率之间的非线线关系

设采样周期T=2s（采样周期T不参与设计， 取2s计算最简）， 转化后的过渡模拟滤波器技术指标为Ωp=0.5095rad/s， Ap=2dB（即0.7943倍）， Ωs=1rad/s， As=10dB （即0.3162倍）. 过渡模拟滤波器的技术指标参见图2（c）中的点状图.

（3） 按照虚构的过渡模拟滤波器技术指标设计过渡模拟滤波器系统函数［5］. 过滤模拟滤波器的最低阶次及3dB频率计算公式为：

其中， ［x］表示不超过实数x的最大整数. 代入过渡模拟指标数据， 算得N=3， Ωcp=0.5572 rad/s ， Ωcs= 0.6934 rad/s. 根据最小阶次N直接得到归一化原型系统函数

这里取Ωc=Ωcp， 代入（8）式算得

过渡模拟低通滤波器的幅频曲线如图2（c）所示. 因取Ωc=Ωcp， 所以设计的过渡模拟滤波器通带边界指标精确满足， 而阻带边界指标留有余量.

（4）用双线性变换法将设计的过渡模拟滤波器系统函数转变成数字滤波器系统函数. 取T=2s， 将（5）式代入（9）式并化简得

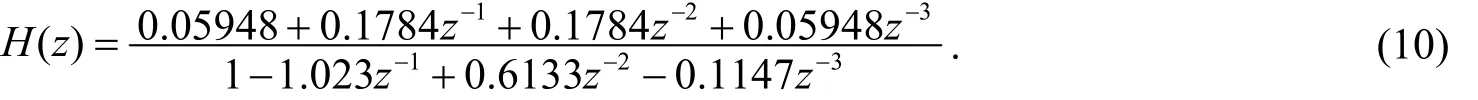
用双线性变换法设计的数字低通滤波器幅频曲线如图2（a）所示， 与图2（c）对比可知幅频曲线的形状差别较大， 这是由于双线性变换法中频率的非线性关系引起的.

2　设计过程的深入分析

2.1过渡模拟滤波器

间接设计IIR数字滤波器， 要先设计一个过渡模拟滤波器， 过渡模拟滤波器可根据数字指标自定义一个采样周期T进行虚构. 后面的分析可知采样周期T不参与设计， T值不同， 算得的过渡模拟指标会不同，由此设计的过渡模拟滤波器也肯定不同， 但按同一T值进行转换得到的数字滤波器是一样的. 如果数字滤波器的技术指标是以数字指标形式给出， 则无需再给出采样周期或采样频率； 若是以模拟指标形式给出，则一定要注意设计指标中用于离散连续信号的采样周期sT和用于设计过渡模拟滤波器的采样周期T不是同一个概念， 前者用于计算数字指标， 后者用于虚构模拟指标. 一些教材中混用了这两个符号， 有的还直接用T=Ts设计过渡模拟滤波器， 理论上虽然可行， 但学生可能会认为过渡模拟滤波器必须这样设计， 既误导了学生， 也增加了计算难度， 甚至还会引起较大误差， 设计中应尽量避免.

2.2频率预畸变校正

进行非线性变换， 则设计的Ha（s）按（4）式变换得到的H（z）一定满足边界频率要求. 图2（c）给出了通带指标精确满足的模拟滤波器幅频特性曲线， 图2（a）给出了变换后数字滤波器的幅频特性曲线， 其通带指标也精确满足. 假如用Ωp=ωpT ， Ωs=ωsT 作为过渡模拟滤波器的边界频率， 则设计的Ha（s）按（4）式变换得到的H（z）就不会满足边界频率要求. （11）式中的Ω与ω的非线性关系， 称为频率预畸变校正.

2.3变换常数C对设计的影响

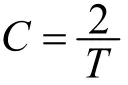
2.4采样周期T对设计的影响

在双线性变换法的设计过程中有一个参数T， 其实设计过程中的参数T只影响变换常数C， 而C的取值不影响设计， 所以参数T也不影响设计. 当然， 采样周期T不影响设计还应从图2所示的坐标变换中进行理解. 对任一给定的变换常数C， 采样周期T对从ω到Ω1的影响和从Ω1到Ω的影响可以相互抵消. 也就是说， C一定时， 采样周期T会影响图2（a）到图2（b）的坐标变换， 也会影响图2（b）到图2（c）的坐标变换，这两种影响正好使图2（a）到图2（c）的坐标变换与T无关. 理论上， 采样周期T对设计结果没有影响， 但由于在设计过程中T参与了计算， 考虑到计算机的有限字长效应和计算简单， 一般取T=2s.

3　MATLAB实现程序

用双线性变换法设计实例中所要求的滤波器程序如下：

%技术指标： Fs=20kHz，fp=3kHz，fs=5kHz，Ap=2dB，As=10db，

clc； close all； clear； format compact；

wp=0.3*pi， ws=0.5*pi， ap=2， as=10， Ts=1/20000；%输入数字技术指标

T=2，%改变T值不影响设计结果

Wp=（2/T）*tan（wp/2）， Ws=（2/T）*tan（ws/2）， Ap=ap， As=as， %双线性变换法指标转换

Mn=log10（（10^（0.1*Ap）-1）/（10^（0.1*As）-1）），Md=（2*log10（Wp/Ws）），%先算分子分母

N=ceil（Mn/Md），%计算过渡模拟滤波器最小阶次

Wcpd=（10^（0.1*Ap）-1）^（1/（2*N）），Wcsd=（10^（0.1*As）-1）^（1/（2*N））， %先算分母

Wcp=Wp/Wcpd； Wcs=Ws/Wcsd； %计算截止频率

Wc=Wcp，%通带精确满足，取Wc=Wcs时阻带精确满足

［bp1，ap1］ = butter（N，1，'s'）； %%计算归一化低通原型模拟滤波器的系统函数Ga（p）

tf（bp1，ap1， 'variable'， 'p'）， %%显示归一化低通原型模拟滤波器的系统函数

［bs，as］ = lp2lp（bp1，ap1，Wc）； %%计算过渡模拟低通滤波器的系统函数Ha（s）

tf（bs，as）， %%显示过渡模拟滤波器的系统函数

［bz，az］ = bilinear （bs，as，1/T），%将过渡模拟滤波器转换为数字滤波器

tf（bz，az，Ts，'variable'，'z^-1'），%显示设计的数字滤波器系统函数

freqz（bz，az，200），%绘图并验证设计技术指标

该程序的运行结果在MATLAB的命令窗或图形窗中直接显示. 从图形窗中显示的幅频曲线可以直接测出ω=0.3π时衰减为2dB， ω=0.5π时衰减为15.37dB， 通带指标精确满足， 阻带指标富有余量. 如果改用Ωc=Ωcs重新设计， 测出ω=0.3π时衰减0.6352dB， ω=0.5π时衰减10dB， 通带指标富有余量， 阻带指标精确满足.改变采样周期T， 设计结果相同.

4　结束语

［1］ 张登奇， 彭 鑫. 脉冲响应不变法在IIR滤波器设计中的应用［J］. 湖南理工学院学报（自然科学版）. 2015（04）： 23～26

［2］ 吴镇扬. 数字信号处理的原理与实现［M］. 南京： 东南大学出版社， 2001： 77

［3］ 李芬华. 双线性变换中的映射［J］. 河北大学学报（自然科学版）. 1991（02）： 65～71

［4］ 吴湘淇. 信号、系统与信号处理（下）［M］. 北京： 电子工业出版社，1996： 60～67

［5］ 刘顺兰， 吴 杰. 数字信号处理［M］. 西安： 西安电子科技大学出版社， 2003： 158

［6］ 高西全， 丁玉美. 数字信号处理［M］. 第3版. 西安： 西安电子科技大学出版社， 2008： 184～189

Application of the Bilinear Transformation in IIR Digital Filter Design

ZHANG Deng-qi， PENG Xin， CHEN Hai-lan
（College of Information and Communication Engineering， Hunan Institute of Science and Technology， Yueyang 414006， China）

Digital filter design is the most important component in teaching of digital signal processing. Bilinear Transformation Method is an important method in the indirect design of IIR filter. We deduce the procedure of IIR filter design based on the fundamentals of Bilinear Transformation. And taking Butterworth low pass filter for instance， we introduce the design steps of filter. Furthermore， we deeply analyze that the unintelligible steps in the design procedure including transitional filters and frequency prewarping. And then， the value of transform constant and sampling period is discussed. Finally， the MATLAB source code of the filter design is given.

digital filter； bilinear Transformation； frequency prewarping transformation； MATLAB

TN713.7

A

1672-5298（2016）03-0021-05

2016-04-28

湖南省自然科学基金项目（14JJ3130）； 湖南省教育厅重点项目（12A057）； 湖南理工学院教学改革研究项目（2014B20）

张登奇（1968- ）， 男， 湖南临湘人， 硕士， 湖南理工学院信息与通信工程学院副教授. 主要研究方向： 信号与信息处理