非对称不定椭圆方程的两网格内罚间断有限元方法
2016-11-05钟柳强刘春梅
钟柳强, 李 莹, 刘春梅
(1.华南师范大学数学科学学院, 广州 510631; 2.湖南科技学院理学院, 永州 425199)
非对称不定椭圆方程的两网格内罚间断有限元方法
钟柳强1*, 李莹1, 刘春梅2
(1.华南师范大学数学科学学院, 广州 510631; 2.湖南科技学院理学院, 永州 425199)
针对一类非对称或不定椭圆方程的内罚间断有限元方法,设计和分析了相应的两网格求解算法.首先给出了内罚间断有限元解的适定性,及其在L2和间断H1范数下的先验估计;其次设计了相应的两网格求解算法,并给出算法的误差分析;最后,数值实验结果验证了算法的高效性.
非对称不定椭圆方程; 内罚间断有限元方法; 两网格方法; 误差估计
令Ωì2是一个单连通有界Lipschitz多边形开区域, 其边界记为∂Ω.考虑如下二阶椭圆偏微分方程:

(1)

(2)
其中微分算子为

(3)
这里系数α(x)满足

(4)


(5)
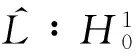
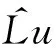
(6)
故其伴随算子





‖φ‖H2(Ω)≤C‖g‖L2(Ω).
(7)
间断有限元方法是对椭圆方程(组)进行数值求解的一种基本离散化方法,通常具有局部守恒性、稳定性及高阶精度,且能较好地解决一些复杂的问题: 例如在不同的求解区域中所求解的方程(组)类型发生改变, 三角网格剖分中允许出现悬点, 较容易实现h-p自适应等.间断有限元方法近年来广泛运用于椭圆方程[1-2].关于间断有限元方法的综述性论文可参见文献[3].
相对于协调元方法, 间断有限元方法离散线性代数系统具有更大的自由度.为了间断有限元方法的高效实现, 需要构造相应的快速算法.两网格方法最初被用于解决非对称不定线性椭圆偏微分方程的协调有限元方法离散线性代数系统[4-5],其基本思想是先在粗网格空间中求解原非对称不定问题,然后在细网格空间中求解相应的对称正定问题. 注意到,在粗网格中解非对称不定问题的工作量是较小的,所以要解决原问题的关键在于怎样在细网格中求解对称正定问题.之后,两网格方法还被用来求解特征值问题[6-7]、拟线性问题[8]以及电磁场问题[9]等等.
BI和GINTING[8]首次将对称内罚间断有限元方法与两网格结合使用,但仅考虑如下对称正定椭圆方程:
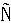

其中αL≤α(u)≤αU, αL和αU是正常数. 最近,CONGREVE等[10]针对如下二阶拟线性椭圆边值问题:
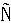

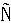
本文将针对非对称或不定椭圆方程边值问题(1)、(2),给出了相应的内罚间断有限元方法, 通过证明相应的Gråding不等式和标准的对偶估计等, 得到当网格尺寸充分小及罚参数充分大时离散变分问题的适定性; 证明了有限元解在L2范数和间断H1范数下的最优误差估计;设计和分析了两网格内罚间断有限元方法;并用数值例子验证了算法的高效性.
在本文中,除了特殊常数外,为避免重复使用一般的常数记号,采用记号、和≈,即当存在正常数C1、C2和C3,满足x1≤C1y1、x2≥C2y2、x3≤y3≤C3x3时,简记为x1y1、x2y2、x3≈y3.
1 内罚间断有限元方法
1.1内罚间断有限元方法的变分问题
在给出边值问题(1)、(2)的连续和离散变分问题之前, 先引入若干定义和记号.
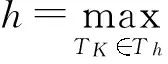

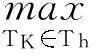

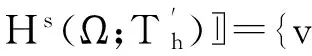
及其范数和半范数分别为:
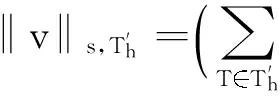
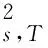
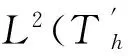
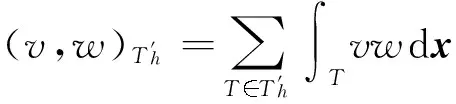
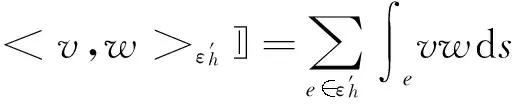

定义 Vh是间断有限元空间:

其中Pr(T)表示定义在T上阶数不大于r的多项式集合,r≥1是某一整数. 显然有VhìHs(Ω;Th).

[[m]]=m+n++m-n-,{{m}}=(m++m-)/2,



其中n是e指向Ω外部的单位外法向量.
方便起见, 将H1(Ω;Th)上的间断H1-范数定义为 :
u2σ=‖u‖,
(8)
及
u21,σ=u‖{{u}}‖,
(9)



(10)
(11)
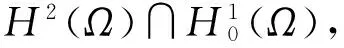

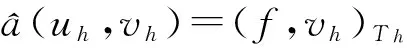
(12)

1.2内罚间断有限元方法解的适定性


引理2[11]14(迹不等式)存在一个正常数C>0,使得
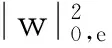
(13)


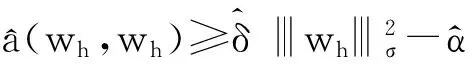
成立.
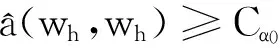
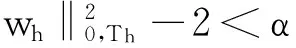

(14)
由式(4)和Cauchy-Schwarz不等式,有
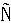

(15)
另外, 根据利用式(5)、Cauchy-Schwarz不等式、局部逆估计(13)及网格的形状正则性, 有
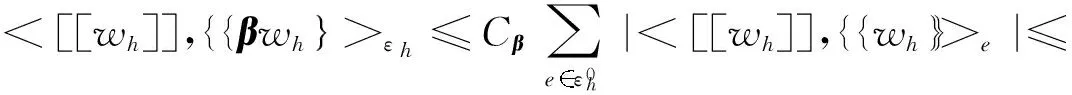
(16)
因此, 综合式(15)、(16)和均值不等式可知
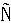
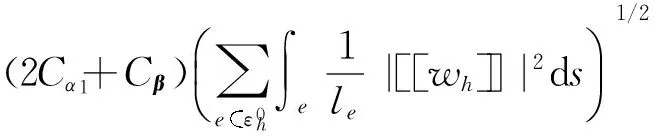
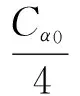
(17)
其中σ1=σ1(Cβ,Cα1,Cα0).
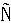
(18)
将式(17)、(18)代入式(14),直接计算
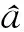
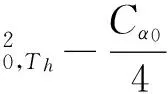
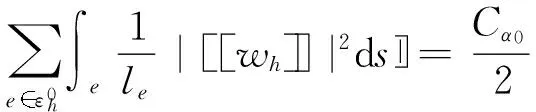
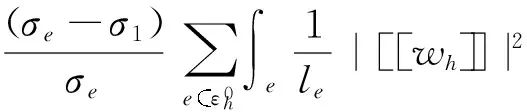
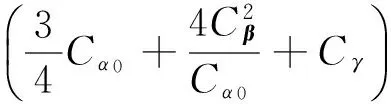
(19)
令
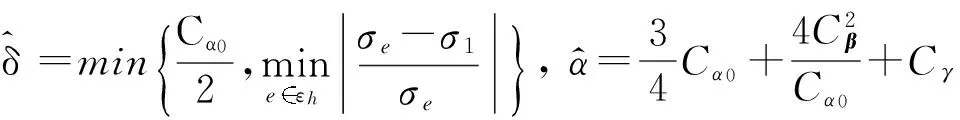


(20)
类似文献[12]157中式(3.8)、(3.9)的证明, 利用迹定理及引理4,得到如下逼近性质.
‖w-χ‖0,T h^Hs‖w‖s,T h,
(21)
且
w-χ1,σ^hs-1‖w‖s,T h,
(22)
其中C依赖于σL.
接下来, 给出标准的对偶论证.

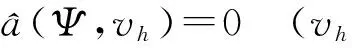
(23)
的解,则存在正常数C,使得
‖Ψ‖0,T h^hΨ1,σ.
(24)
证明考虑如下辅助问题:




hΨ1,σ‖Ψ‖0,T h,
(25)
式(25)两边消去‖Ψ‖0,T h,即证得式(24).
下面给出离散变分问题(12)解的适定性证明. 其证明思想类似于文献[13]的定理证明, 证明过程需要用到引理3和引理6.

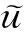
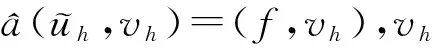
(26)

(27)

(28)
1.3内罚间断有限元方法的先验估计
下面的定理将给出IPDG法的最优误差估计,它将用于下一节两网格法的收敛性分析.

uh-u1,σ^hs-1‖u‖s,T h,2≤s≤r+1,
(29)
‖uh-u‖0,T h^huh-u1,σ.
(30)

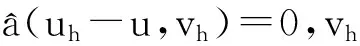
(31)
由引理6得到‖uh-u‖0,T h^huh-u1,σ.
其次证明式(29). 由引理6和三角不等式,有
‖uh-u‖0,T h^uh-u1,σh^
(32)
其中χ由引理5给出.
利用三角不等式及式(32), 有
‖uh- χ‖0,T h^‖uh-u‖0,T h+‖u- χ‖0,T h^
huh- χ1,σ+(h+1)‖u- χ‖1,T h.

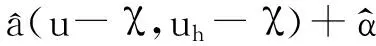
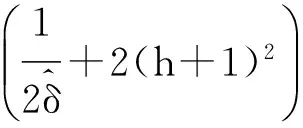
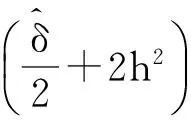
(33)
当h充分小时可得到
uh-χσ^u-χ1,σ.
(34)
故利用三角不等式、引理1、式(34)及式(22),有
2 两网格方法及其收敛性分析
2.1两网格方法
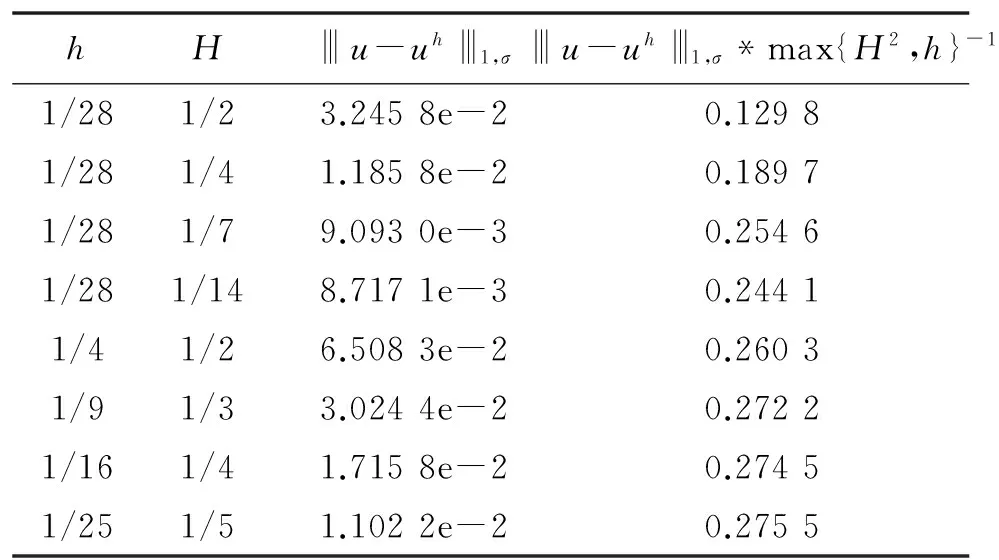
XU[4-5]就椭圆问题的两网格算法做了详细的论述. 两网格算法的基本思想是给出Ω的2个满足形状规则的嵌套网格剖分, 不妨记作TH和Th, 这里H和h是2个不同的网格尺寸, 且满足h< (35)及 (36) (37) (38) 注3求解非对称正定问题在第2步的时候已经化为求解一个对称问题. 2.2误差分析 a(vh,vh)vh21,σ, (39) 其中σ2=σ2(Cα1,Cα0).同时有 a(uh,uh)^uh1,σvh1,σ,∀vhVh; (40) 式(39)、(40)的常数依赖于σL,Cα1,Cβ,Cγ. N(uh,vh)^‖uh‖0,T h‖vh‖σ, (41) 式中正常数依赖于Cβ,Cγ,σL. 证明由N(uh,vh)的定义可知 (uh,vh)T h-<[[uh]],{{βvh}}>εh. (42) 接下来估计N(uh,vh)中的每一项. (43) 从而有 (44) 以下估计式(44)中最后2项. 先看右边第1项,由三角不等式、Cauchy-Schwarz不等式、引理2及如下不等式[1]1689 可知 (45) ‖vh‖1,T h‖uh‖0,T h. (46) 最后, 估计式(42)右边其余2项. 同样由Cauchy-Schwarz不等式可知 (γuh,vh)T h-(uh,vh)T h^‖uh‖0,T h‖vh‖0,T h. (47) ‖uh‖0,T h‖vh‖1,T h^‖uh‖0,T hvhσ. 至此, 证明完毕. uh-uh1,σ^Hr+1‖u‖r+1,T h, (48) u-uh1,σ^(hr+Hr+1)‖u‖r+1,T H. (49) 证明首先证明式(48). 利用式(36)、(38)和引理8, 可以得到 a(uh-uh,vh)=a(uh,vh)-a(uh,vh)= (f,vh)-N(uh,vh)-[(f,vh)-N(uH,vh)]= N(uH-uh,vh)=N(uH-u,vh)+N(u-uh,vh)^ (‖u-uH‖0,T h+‖u-uh‖0,T h)vh1,σ. (50) 特别地, 令式(50)中vh=uh-uh, 再利用引理7及引理8, 可知 (‖u-uH‖0,T h+‖u-uh‖0,T h)uh-uh1,σ. (51) uh-uh1,σ^ ‖u-uH‖0,T h+‖u-uh‖0,T h. 因为uH、uh是问题(12)在2种网格尺寸剖分下的解, 利用定理2易知 Hr+1‖u‖r+1,T H+hr+1‖u‖r+1,T h≤ Hr+1(‖u‖r+1,T H+‖u‖r+1,T h)^ Hr+1‖u‖r+1,T h. 其次, 证明式(49), 利用定理2及式(48), 有 hr‖u‖r+1,T h+Hr+1‖u‖r+1,T H^ (hr+Hr+1)‖u‖r+1,T h. 综上所述, 定理3证毕. 本节将针对问题(1)、(2)给出一些数值实验来验证定理3的理论结果, 从而验证两网格算法的高效性. 在所有实验中, 取计算区域为Ω=(0,1)2, 网格剖分Th由Ω通过一致加密得到. 在方程(1)、(2)中取α=1, β=(0,0)T,γ=10,此时方程(1)、(2)变为如下形式: 表1验证了式(48), 即固定细网格尺寸h, 取不同的粗网格尺寸H时, 可以观察到uh-uh1,σ*H-2趋于某一常数. 表1两网格解与有限元解的逼近误差 Table 1Approximation error between two-grid method and finite element solution hHuh-uh1,σuh-uh1,σ*H-21/321/23.1142e-20.12471/321/47.8870e-30.12621/321/81.8790e-30.12031/321/163.7761e-40.09671/641/47.9761e-30.12761/641/81.9587e-30.12541/641/164.5483e-40.11641/641/327.2877e-50.0746 表2验证了式(49),此时固定细网格尺寸h, 取不同的粗网格尺寸H, 或令粗网格尺寸H与细网格尺寸h满足平方关系, 都有u-uh1,σ*max{H2,h}-1也趋于某一常数. 表2两网格解与有限元解的逼近误差 Table 2Approximation error between two-grid method and finite element solution hHu-uh1,σu-uh1,σ*max{H2,h}-11/281/23.2458e-20.12981/281/41.1858e-20.18971/281/79.0930e-30.25461/281/148.7171e-30.24411/41/26.5083e-20.26031/91/33.0244e-20.27221/161/41.7158e-20.27451/251/51.1022e-20.2755 [1]CASTILLO P,COCKBURN B,PERUGIA I,et al. An a priori error analysis of the local discontinuous Galerkin method for elliptic problems[J]. Siam Journal on Numerical Analysis,2001,38(5):1676-1706. [2]COCKBURN B,KANSCHAT G,PERUGIA I,et al. Superconvergence of the local discontinuous Galerkin method for elliptic problems on Cartesian grids[J]. Siam Journal on Numerical Analysis,2002,39(1):264-285. [3]COCKBURN B,KARNIADAKIS G E,SHU C W.Discontinuous Galerkin methods: theory, computation and app-lications[M]. Berlin: Springer, 2000:3-50. [4]XU J. A novel two-grid method for semilinear elliptic equations[J]. Siam Journal on Scientific Computing,1994,15(1):231-237. [5]XU J. Two-grid discretization techniques for linear and nonlinear PDEs[J]. Siam Journal on Numerical Analysis, 1996,33(5):1759-1777. [6]XU J,ZHOU A. A two-grid discretization scheme for eigenvalue problems[J]. Mathematics of Computation,2001,70:17-25. [7]CHIEN C,JENG B. A two-grid discretization scheme for semilinear elliptic eigenvalue problems[J]. Siam Journal on Scientific Computing,2006,27(4):1287-1304. [8]BI C,GINTING V.Two-grid discontinuous Galerkin method for quasi-linear elliptic problems[J].Journal of Scientific Computing,2011,49(3):311-331. [9]ZHONG L,SHU S,WANG J,et al. Two-grid methods for time-harmonic Maxwell equations[J]. Numerical Linear Algebra with Applications,2013,20(1):93-111. [10]CONGREVE S,HOUSTON P,WIHLER T P. Two-grid hp-version discontinuous Galerkin finite element methods for secondorder quasilinear elliptic PDEs[J]. Journal of Scientific Computing,2013,55(2):471-497. [11]张铁.间断有限元理论与方法[M].北京:科学出版社,2012. [12]WHEELER M F. An elliptic collocation-finite element method with interior penalties[J]. Siam Journal on Numerical Analysis,1978,15(1). [13]SCHATZ A H. An observation concerning Ritz-Galerkin methods with indefinite bilinear forms[J]. Mathematics of Computation,1974,28:961. 【中文责编:庄晓琼英文责编:肖菁】 Two-Grid IPDG Method for Non-Symmetric Indefinite Elliptic Equations ZHONG Liuqiang1*, LI Ying1, LIU Chunmei2 (1.School of Mathematical Sciences, South China Normal University, Guangzhou 510631, China; 2.College of Science, Hunan University of Science and Engineering, Yongzhou 425199, China) A two-grid interior penalty discontious Galkerkin (IPDG) method for non-symmetric indefinite elliptic equations is proposed. Firstly, the well-posedness of IPDG method and the optimal error estimates in bothL2norm and discontinuousH1norm are proved. Then, the corresponding two-grid method is designed and the error estimate of the algorithm is provided. At last, the efficiency of the algorithm is validated by numerical experiments. non-symmetric indefinite elliptic equation; interior penalty discontious Galkerkin method; two-grid method; error estimates 2016-02-26《华南师范大学学报(自然科学版)》网址:http://journal.scnu.edu.cn/n 国家自然科学基金项目(11201159);全国博士学位论文作者专项资金项目(201212);广东省高等学校优秀青年教师培养计划专项(Yq2013054);湖南省自然科学基金项目(14JJ3135);广州市珠江科技新星项目(2013J2200063) 钟柳强, 教授,Email:zhong@scnu.edu.cn. O A

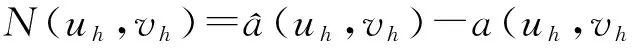

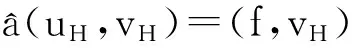




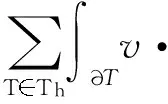

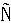
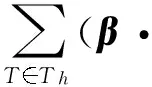
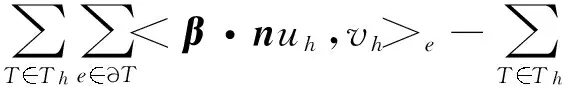
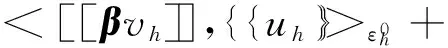


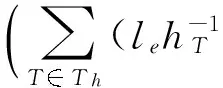
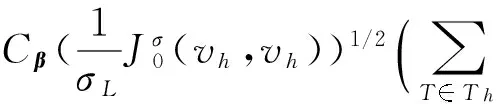
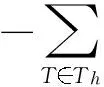
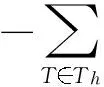

3 数值例子