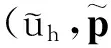非线性双曲型方程的混合有限元两层网格算法
2016-11-05陈艳萍王克彦
陈艳萍, 王克彦
(华南师范大学数学科学学院,广州 510631)
非线性双曲型方程的混合有限元两层网格算法
陈艳萍*, 王克彦
(华南师范大学数学科学学院,广州 510631)
针对一类非线性双曲型方程, 利用混合有限元法,构造了1种混合有限元两层网格算法, 给出了两网格方法的误差分析. 结果表明, 当两层网格算法所选取的粗网格和细网格步长满足H=O(h1/2)时,能获得渐近最优的离散逼近解. 并用数值例子验证了该混合有限元两层网格算法的有效性.
非线性双曲型方程; 混合有限元; 两层网格算法; 误差分析
考虑下述非线性双曲型方程的混合问题:
(1)
(A1)κ=K-1是一致对称正定的矩阵, 即存在常数K*,K*>0, 使得
K*|y|2≤yTκ(x,t)y≤K*|y|2.
(2)
(A2)f=f(u)为已知的有界光滑函数, 且存在常数K1, 使得
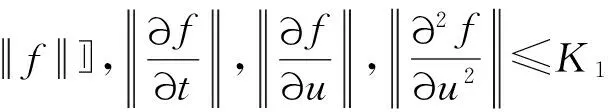
(3)
(A3)对于r>0, 假设满足式(1)的解函数u有下列正则性



(4)
双曲型方程描述声波、光波、多孔介质波传播问题和流体力学等众多物理现象,对许多实际问题具有重要的理论价值及现实意义.目前, 许多数值求解方法被应用到双曲问题, 如有限差分法[1-2]、有限元法[3-4]和有限体积元法[5-6]等等.
混合有限元方法是在有限元方法的基础上发展起来的一个分支, 已成为偏微分方程数值求解的一种重要方法. 20世纪70年代, BABUSKA[7]和BREEZZI[8]基于B-B相容性条件获得了混合有限元方法的一般理论. FALK和OSBORN[9]改进了该方法,推广了混合有限元方法的适应性. RAVIART和THOMAS[10]针对二阶椭圆问题, 提出了R-T混合有限元的构造方法,通过引入中间变量将高阶微分方程降阶, 从而降低了对有限元空间的光滑性要求, 与标准有限元只能通过后处理对微分算子进行计算相比, 其数值解的精度往往会提高. 在过去的几十年里, 混合有限元方法得到了广泛的应用[11-13].
两层网格算法是一类求解非线性偏微分方程的高效算法, 它的基本思想是: 通过构造2种不同尺度(粗网格和细网格)的有限元空间, 首先在粗网格上求解原来的非线性问题, 然后利用粗网格上的数值解将原问题用合适的方式进行线性化, 再在细网格上求解相应的线性化问题. 该方法最先由XU[14-15]提出和讨论, 他将两层网格思想与非线性Galerkin方法相结合,成功运用于求解半线性和非线性椭圆型问题. 随着对这种高效的有限元两层网格算法研究的深入,许多学者已经将它应用于各类不同的、具有实际应用背景非线性的偏微分方程问题. DAWSON等[16]研究了非线性问题的有限差分两层网格方法; WU和ALLEN[17]使用了扩展混合有限元两层网格方法研究了半线性反应扩散方程; HOLST等[18]分析了半线性界面问题的两层网格算法; ZHOU等[19]研究了Maxwell特征值问题两层网格算法; CHEN等[6,20]分别使用两网格有限元和两网格有限体积元法研究了双曲型方程; 最近, CHEN等[21-23]研究了针对抛物型方程问题的混合有限元两网格方法.
本文针对非线性双曲型方程构造了混合有限元两层网格算法, 通过将非线性问题的求解转化为1个节点数较少的粗网格上的非线性问题和1个细网格上的线性问题, 使问题在一定程度上得到了线性化, 从而加快了非线性问题的求解速度.同时给出了两层网格法的误差分析, 根据误差估计和数值算例可知两层网格算法在不降低解的精度的情况下提高了计算效率.
1 主要符号及投影算子的逼近性质


‖υ‖H(div;Ω)≡(‖υ‖2+‖▽·υ‖2)1/2.

设Qh为L2投影算子,则有



‖Qhφ‖0,q≤C‖φ‖0,q(2≤q<∞),
‖φ-Qhφ‖0,q≤C‖φ‖r,qhr(0≤r≤k+1).
(5)
同时利用标准混合有限元空间的Fortin投影算子Πh:(H1(Ω))2Vh, 使得对任意的qH(div,Ω),有


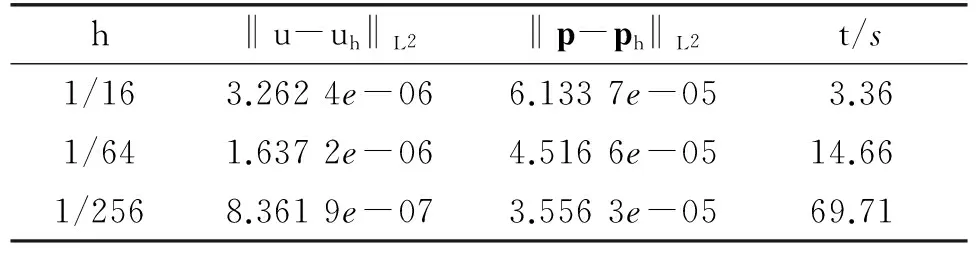
‖q-Πhq‖0,q≤C‖q‖r,qhr(1/q (6) ‖▽·(q-Πhq)‖0,q≤C‖▽·q‖r,qhr(0≤r≤k+1). 对于空间Wh和Vh, 具有逆估计 ‖w‖0,∞≤Ch-1‖w‖,‖υ‖0,∞≤Ch-1‖υ‖ (7) (8) 对方程(8)离散化, 可得 (9) (10) (11) (12) 由方程(8)和方程(12), 得到误差方程 (13) 为了后面的理论分析,给出以下引理. ‖p-Rhp‖0,q≤C‖p‖k+1,qhk+1, ‖▽·(p-Rhp)‖0,q≤C‖▽·p‖k+1,qhk+1. ‖u-Rhu‖0,q+‖(u-Rhu)t‖0,q≤C‖u‖r,qhr, ‖Qhu-Rhu‖0,q+‖(Qhu-Rhu)t‖0,q≤C‖u‖r+1,qhr+1. ‖utt-Rhutt‖≤C(‖utt‖r+1+‖ut‖r+2+‖u‖r+2)hr, ‖utt-Rhutt‖0,∞≤C(‖utt‖r,∞+‖utt‖r+1+‖ut‖r+2+‖u‖r+2)hr, ‖Qhutt-Rhutt‖≤C(‖utt‖r+1+‖ut‖r+2+‖u‖r+2)hr+1. 下面将得到全离散混合有限元解和椭圆混合法投影之间的超收敛现象. 为了分析方便, 记αn=un-Rhun,γn=pn-Rhpn,δn=Qhun-Rhun. C(hk+2+Δt2). (14) 证明方程(13)可写为: (15) (κ(pn+1-Rhpn+1),υh)-(▽·υh,un+1-Rhun+1)=0 (16) 由方程(8)可得 (17) (18) (19) (20) (21) (T1,∂tξn)+(T2,∂tξn)+(T3,∂tξn). (22) 式(22)两端同乘以2Δt并对t从1到l-1(1 接下来利用文献[12]185-187中引理6的证明方法, 可获得方程的全离散解和椭圆混合法投影之间的超收敛结果(式(14)). 进一步, 利用三角不等式、引理1~引理3及引理5可获得混合有限元的误差估计. C(hk+1+Δt2). 本节构造了非线性双曲型方程(1)的全离散两网格混合有限元格式.对区域Ω进行2个拟一致三角形网格剖分TH和Th,得到有限维空间WH×VH(⊂Wh×Vh).此算法可以分为2步进行: 首先在粗网格TH上解1个非线性问题(即原问题); 然后在细网格Th上解1个线性问题(即原问题线性化). 算法如下: (23) (24) (25) (26) (27) (28) (29) 证明利用三角不等式、 逼近性质(5)、引理2、引理5及逆估计(7), 易得到式(29). (30) 那么存在与h和Δt无关的C,使得 C(hk+1+H2k+2+Δt2). (31) (32) (κωn+1,υh)-(▽·υh,μn+1)=-(κn+1,υh), (33) (34) (F1,∂tμn)-(κ∂t). (35) 式(35)两边同乘以2Δt, 对t从1到l-1(1 (κ∂t}. (36) (37) (38) 下面估计方程(36)的右端,有 (39) 对于F1中的每一项, 利用逼近性质(5)、引理4和引理6, 可以得到 (40) (41) (42) 由式(40)~(42), 得到F1的估计如下: (43) (44) (45) 在式(45)两边同时加上‖μl‖, 并使用不等式 利用离散的Gronwall引理可得 C{Δt4+h2k+2+H4k+4}. 最后, 由逼近性质(5)、式(6)以及三角不等式,式(31)成立. 考虑非线性双曲型方程问题 (46) 由表1和表2可知, 两网格法得到的数值解与直接法求得的结果几乎一致, 同时通过比较计算时间t(利用MATLAB软件的运行时间)可知, 两网格法提高了计算效率, 当计算规模较大的时候, 更能体现两网格法的优势. 这些结果和理论分析的结果一致.该方法简单有效, 我们可以知道当粗网格十分粗时, 即粗网格的网格数比细网格的网格数小得多, 不会影响细网格上有限元方法解的精度, 这样可以将大规模的计算问题转化成小规模问题进行求解. 表1 混合有限元法计算误差及时间 表2 两层网格法计算误差及时间 [1]WIRZHJ,SCHUTTERFD,TURIA.Animplicit,compact,finitedifferencemethodtosolvehyperbolicequations[J].MathematicsandComputersinSimulation,1977,19:241-261. [2]KABANIKHINSI.Afinite-differencemethodoffindingthecoefficientsofahyperbolicequation[J].USSRComputationalMathematicsandMathematicalPhysics,1979,19:150-159. [3]DUPONTT. L2estimatesforGalerkinmethodsforsecondorderhyperbolicequations[J].SiamJournalonNumericalAnalysis, 1973,10(5):880-889. [4]BAKERGA.Errorestimatesforfiniteelementmethodsforsecondorderhyperbolicequations[J].SiamJournalonNumericalAnalysis,1976,13(4):564-576. [5]KUMARS,NATARAJN,PANIAK.Finitevolumeelementmethodforsecondorderhyperbolicequations[J].InternationalJournalofNumericalAnalysis&Modeling,2008,5(1):132-151. [6]CHENCJ,LIUW.Atwo-gridmethodforfinitevolumeelementapproximationsofsecond-ordernonlinearhyperbolicequations[J].JournalofComputationalandAppliedMathematics, 2010,233(11):2975-2984. [7]BABUSKAI.Errorboundsforfiniteelementmethod[J].NumerischeMathematik,1971,16:322-333. [8]BREZZIF.Ontheexistence,uniquenessandapproximationofsaddle-pointproblemsarisingfromLagrangianmultipliers[J].SiamJournalonNumericalAnalysis, 1974,8:129-151. [9]FALKRS,OSBORNJE.Errorestimationsformixedmethods[J].RAIROAnalyseNumerique,1980,14:249-277. [10]RAVIARTPA,THOMASTM.Amixedfiniteelementmethodforsecondorderellipticproblems[M]∥GALLI-GAMI,MAGENESE.MathematicalaspectsofFEM.Berlin:Springer, 1977,606:292-315. [11]COWSARL,DUPONTT,WHEELERMF.Aprioriestimatesformixedfiniteelementmethodsforthewareequation[J].ComputerMethodsinAppliedMechanicsEngineering,1990,82(1/2/3):205-222. [12]CHENYP,SHENZH,HUANGYQ.Errorestimatesforthefull-discretemixedFEMfornonlinearhyperbolicproblems[J].NumericalMathematics,2000,9(2):181-192. [13]CHENYP,HUANGYQ.Improvederrorestimatesformixedfiniteelementfornonlinearhyperbolicequations:thecontinuous-timecase[J].JournalofComputationalMathematics, 2001,19(4):385-392. [14]XUJ.Anoveltwo-gridmethodforsemilinearequations[J].SiamJournalonScientificComputing,1994,15(1):231-237.[15]XUJ.Two-griddiscretizationtechniquesforlinearandnon-linearPDEs[J].SiamJournalonNumericalAnalysis,1996,33(5):1759-1777.[16]DAWSONCN,WHEELERMF,WOODWARDCS.Atwo-gridfinitedifferenceschemefornonlinearparabolicequations[J].SiamJournalonNumericalAnalysis,1998,35(2):435-452. [17]WUL,ALLENMB.Atwo-gridmethodformixedfinite-elementsolutionofreaction-diffusionequations[J].NumericalMethodsforPartialDifferentialEquations,1999,15(3):317-332. [18]HOLSTM,SZYPOWSKIR,ZHUYR.Two-gridmethodsforsemilinearinterfaceproblems[J].NumericalMethodsforPartialDifferentialEquations,2013,29(5):1729-1748. [19]ZHOUJ,HUX,ZHONGL,etal.Two-gridmethodsforMaxwelleigenvalueproblems[J].SiamJournalonNumeri-calAnalysis,2014,52(4):2027-2047.[20]CHENCJ,LIUW,ZHAOX.Atwo-gridfiniteelementmethodforasecond-ordernonlinearhyperbolicequation[J].AbstractandAppliedAnalysis, 2014:Art803615,6pp.[21]CHENYP,HUANGYQ,YUDH.Atwo-gridmethodforexpandedmixedfinite-elementsolutionofsemilinearreaction-diffusionequations[J].InternationalJournalforNumericalMethodsinEngineering, 2003,57(2):193-209. [22]CHENYP,LIUHW,LIUS.Analysisoftwo-gridmethodsforreaction-diffusionequationsbyexpandedmixedfiniteelementmehtods[J].InternationalJournalforNumeri-calMethodsinEngineering, 2007,69(2):408-422.[23]CHENYP,LIL. Lperrorestimatesoftwo-gridschemesofexpandedmixedfiniteelementmethods[J].AppliedMathematicsandComputation, 2009,209(2):197-205. [24]GARCIAMF.Improvederrorestimatesformixedfinite-elementapproximationsfornonlinearparabolicequations:thecontinuous-timecase[J].NumericalMethodsforPartialDifferentialEquations,1994,10:139. 【中文责编:庄晓琼英文责编:肖菁】 Two-Grid Scheme for the Mixed Finite Element Approximations of Nonlinear Hyperbolic Equations CHEN Yanping*, WANG Keyan (School of Mathematical Science, South China Normal University, Guangzhou 510631,China) A combination method of mixed finite element method and two-grid scheme is constructed for solving numerically the two-dimensional nonlinear hyperbolic equations. Error estimate are derived in detail. It is shown that two grid algorithm achieve asymptotically optimal approximation of discrete solution as long as the mesh sizes satisfyH=O(h1/2). Numerical example is presented to verify the efficiency and accuracy of the proposed numerical algorithm. nonlinear hyperbolic equations; mixed finite element method; two-grid algorithm; error estimate 2016-04-03《华南师范大学学报(自然科学版)》网址:http://journal.scnu.edu.cn/n 国家自然科学基金项目(91430104, 11271145);广东省自然科学基金项目(2015A030313643);华南师范大学研究生创新基金项目(2015lkxm03) 陈艳萍,教授,珠江学者,Email:yanpingchen@scnu.edu.cn. O241.1 A 1000-5463(2016)03-0001-06
2 混合有限元法及其误差估计


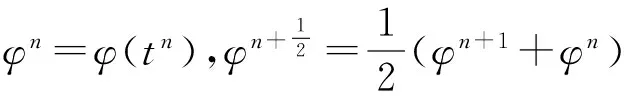
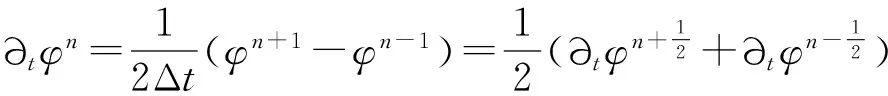
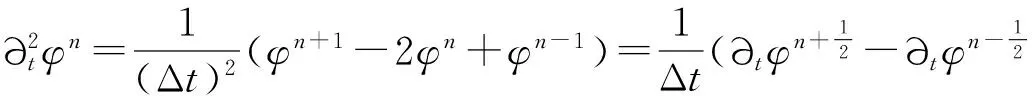









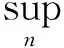
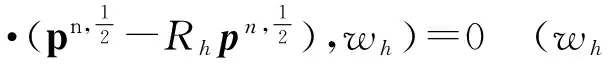

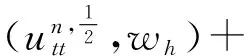


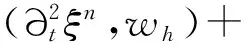

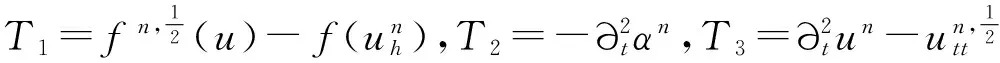

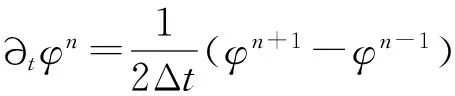

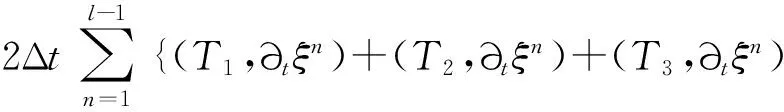
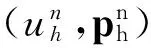
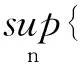
3 两层网格算法及其误差分析


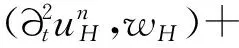


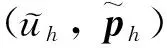
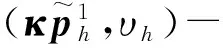
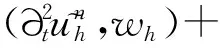

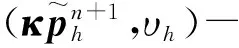


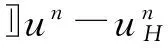


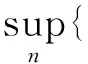





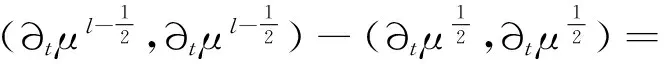
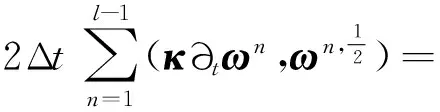

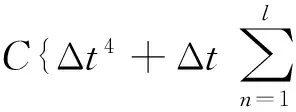
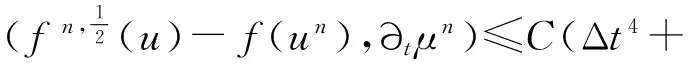
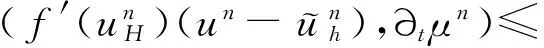
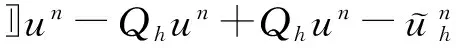


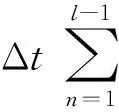



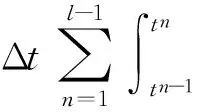

4 数值例子