Disturbed Constitutive Approach to Heat Transfer of Non-Newtonian Nanofluid Flow

HAN Shifang, WU Yueqing, XIAO Fan

(Chengdu Institute of Computer Application, Chinese Academy of Sciences, Chengdu 610041, China)



Disturbed Constitutive Approach to Heat Transfer of Non-Newtonian Nanofluid Flow

HAN Shifang, WU Yueqing, XIAO Fan

(Chengdu Institute of Computer Application, Chinese Academy of Sciences, Chengdu 610041, China)

The non-Newtonian fluid flow theory is applied to study nanofluid motion which is considered as a new concept non-Newtonian fluid. Due to gliding motion of nano particles with respect to basic flow and thermal diffusion disturbed flow caused by random motion of nano-particles, the new concept non-Newtonian fluid is considered as a nearly basic flow, which is generalized by a slightly rotation of basic flow of one phase fluid with respect to the 1,2,3 axes of the Cartesian coordinate system. As an important application of the developed disturbed constitutive theory, the two dimensional thermal flow of nanofluid between two infinite planes is studied. The flow between two infinite planes is treaded as a flow with dominating extension. The developed disturbed constitutive theory can be used for the thermal nanofluid flow.

thermal nanofluid flow; new concept non-Newtonian fluid; disturbed constitutive equation; flow with dominating extension ; computational symbolic manipulation

INTRODUCTION

Presented investigation is a new attempt to apply non-Newtonian fluid flow theory to study nanofluid motion which is considered as a new concept non-Newtonian fluid[1-3].In the present paper non-Newtonian thermal nanofluid flow is studied by disturbed constitutive approach. The disturbed constitutive equation theory for non-Newtonian fluid flow stability is generalized to study thermal nanofluid motion.The attempt is presented to extend principles in research on non-Newtonian fluid flow and rheology[4-5]to study nanofluid motion. In research on energy transfer theory of nanofluid two main approaches were reported[1]:one phase fluid approach and perturbation model for nanofluid. As first approximation the nanofluid can be considered as one phase fluid of uniform mixing. The one phase approach has been well used now by few authors for investigation on nanofluid heat transfer[6-9].Under assumptions that there exit no slip motion between the basic fluid and the dispersed fine particles,also thermal equilibrium between nanoparticles and the fluid is not important,the nanofluid can be treaded as one phase fluid. In general case Brownian force, friction force between fluid and particles, Brownian diffusion, sedimentation, dispersion may coexist in the basic flow of nanofluid.A gliding velocity between fluid and particles may not be zero. Due to the gliding motion of nanoparticles with respect to basic fluid and thermal diffusion the disturbances in velocity and temperature are caused by random motion of nanoparticles. Otherwise the suspended solid particles increase the thermal conductivity of the two phase mixture. Perturbation approach for nanofluid is developed on the base of one phase fluid with correction due small disturbance of nano-particles in nanofluid[1,10].

In non-Newtonian fluid investigation a concept of nearly extensional flow was proposed by Huilgol[11].Han and Becker have extended the concept to study disturbed constitutive theory and stability of the fluid flow[4-5,12-19]. According to disturbed constitutive theory of Han and Becker the disturbed extensional flow can be considered as a nearly extensional flow, or nearly basic flow, which is generalized by a slightly rotation of basic flow with respect to the 1,2,3 axes of the Cartesian coordinate system. The theoretical approach will be now extended to study nanofluid motion. A new concept of nearly basic nanofluid flow is introduced and an original approach - disturbed constitutive approach is developed to study the nanofluid flow. A disturbed flow caused by random motion of nano-particles can be considered as nearly basic flow or nearly one phase fluid flow, which is generalized by a slightly rotation of basic flow of one phase fluid with respect to the 1,2,3 axes of the Cartesian coordinate system. An important application of the developed disturbed constitutive theory two dimensional thermal flow between two infinite planes will be studied. Following the investigation of Zahorski[20-21], the flow between two infinite planes will be considered as a flow with dominating extension, the developed disturbed constitutive theory can be available for the two dimensional nanofluid thermal flow.

1　Disturbed Constitutive theory For Nanofluid Flow

In research on suspension theory Betchelor has developed an ensemble average approach to study the stress system in a suspension of force free particles, Based on the theory for the viscosity of dilute suspension of rigid spheres a constitutive equation can be viewed as a single phase

(1)

wher φ-volume fraction of solid particles in nanofluid. The improved Einstein model is given as

where：ηeff-effective viscosity of two phase fluid, ηf-apparent viscosity of fluid. This is the Einstein result for the viscosity of a suspension of dilute rigid spheres.

Brinkman model is used in research on nanofluid flow[6-9], which is given as

(2)

On the basis of above results the non-Newtonian simple fluid in sense of Noll and Coleman is generalized for nanofluid, the constitutive equation of which is given as

(3)

where Π- generalized stress tensor for simple nanofluid, S-stress tensor for basic simple fluid, Ψ(φ)-nano-constitutive function.

A series of experimental results showed[1]that the viscosity and thermal conductivity of nanofluid are mainly functions of volume fraction of solid particles φ in it, meanwhile for the viscosity of a dilute suspension of rigid spheres the Einstein, improved and Brickman functions are used for one phase fluid model on the basis of which a nano-constitutive function ψ(φ) is introduced in constitutive equation (3) to characterize the special property of two phase nature of nanofluid:

ψ(φ)→1, when φ→0

The nano-constitutive function ψ(φ) is more complex one which depends not only mainly on volume fraction of solid particles φ, but also on particle's diameter, shape, temperature and so on. The present paper is limited to study influence of the main factor -volume fraction of solid particles φ.

The equation (3) is generalized simple fluid for nanofluid. For a sufficiently small disturbance , the disturbance stress is a linear functional of the disturbance part of the right Cauchy strain tensor. Hence, the functional in (3) has an integral representation

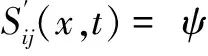
(4)

where k1、k2、k3-kinematic parameters of flow. The concept of short memory is generalized for the magnetic nanofluid too, this means that the kernel functions in above integral expansion are of Maxwell character, the first term of right Cauchy tensor can be expressed by

(5)

(6)

where

(7)

The disturbed constitutive equation (6) can be reduced to

(8)

where

The disturbed constitutive equation theory will be developed to study nanofluid motion. Due to gliding motion of nano particles with respect to basic flow and thermal diffusion a disturbed flow caused by random motion of nano-particles is considered as a nearly basic flow, which is generalized by a slightly rotation of basic flow of one phase fluid with respect to the 1,2,3 axes of the Cartesian coordinate system. The rotation matrix is denoted by δQ

(9)

where the δα1, δα2, δα3are small rotation angles. The nearly basic flow can be considered a small disturbance of the basic flow.

For the perturbation nanofluid fluid the disturbed Rivlin Ericksen tensor and extra stress tensor are assumed to be of

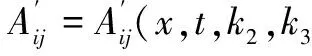
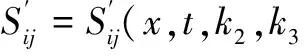
(10)

The disturbance flow is created by the following two factors:

(1) Slightly rotation of basic flow of one phase nanofluid with respect to the 1,2,3 axes of the Cartesian coordinate system;

(2) Variation in kinematic parameters k1, k2, k3of nanofluid flow .

The disturbance Rivlin Ericksen tensor and extra stress tensor are determined by following equations:

(11)

The extensional flow of nanofluid is studied, velocity field of which is given as

v1=k1x1,v2=k2x3,v3=k3x3

(12)

where k1, k2, k3are constant elongation rates in 1,2,3 axes. When the incompressible fluid is considered the relationship of incompressibility is satisfied. But for more general case the condition of incompressibility does not satisfy, the nano-fluid should be compressible one which will be studied

k1+k2+k3≠0

For basic flow the first Rivlin-Ericksen tensor and the stress tensor are given by

(13)

The disturbance Rivlin Ericksen tensor and extra stress tensor are determined by equation (11). Inserting the obtained expressions into equation (8) and taking account of the fact that the δk1, δk2, δk3, δa1, δk2, δk3, can be varied independently, a sufficient number of linear eqns. are obtained which uniquely determine the 36 coefficients kisin equation (8). The result is given.

For the simple incompressible nano-fluid the disturbed stress tensor is reduced to

δk1,δk2,δk3,δα1,δα2,δα3can be varied

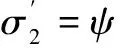
(14)

As an application of the developed disturbed constitutive equation the motion of a stretching sheet of nanofluid will be considered.

2　Thermal flow of nanofluid

An important application of the developed disturbed constitutive theory the Poiseuille thermal flow will be studied. The thermal nanofluid flow is a flow between two infinite planes with distance of 2h. Following the investigation of Zahorski, the flow between two infinite planes will be considered as an evolution of some stretching motion, i.e. as a flow with dominating extension, thereby the above developed disturbed constitutive theory can be available for the two dimensional thermal flow. The velocity field is given. Neglecting inertia in governing equations and taking account of the velocity field the motion equation and energy equation are simplified.

For the nanofluid the Maxwell fluid can be considered as a carrier liquid, the total velocity of the nanofluid is split into two parts; basic Maxwell fluid and nano-disturbed flow. For upper-convected Maxwell fluid the disturbance stress component is given by the disturbed constitutive theory.The following dimensionless variables are introduced

(15)

(16)

where Tm-average temperature of nanofluid flow, Tw-wall temperature at the boundary. For steady process the energy equation is finally reduced to

(17)

The improved Kantorovich variational approach is used to solve equation (17). A series of shape functions is proposed which is given as

(18)

The following operator is defined

(19)

The approximate solution is assumed to be of

T(ξ,η)=(1-η4)φ1(ξ)+(1-η4)η2φ2(ξ)…

(20)

Using the improved Kantorovich approach[4-5] the following integral relationship is satisfied

∫L(Tk)(1-η4)η2(k-1)dηδφkdξ=0

k=1,2…

(21)

The expression of the temperature of 2nd approximation will be following

(22)

In general case the average temperature Tmis calculated by a special form which is a constant for definite ξ

(23)

When the ξ is enough great the temperature field is fully developed Tm. The average temperature can be considered as a constant with respect to ξ. The Nusselt number can be simplified as following

(24)

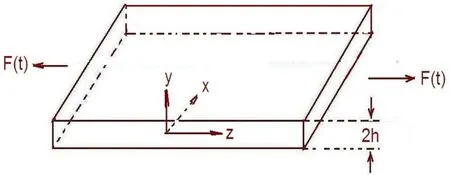
Figure 1flow between two infinite planes

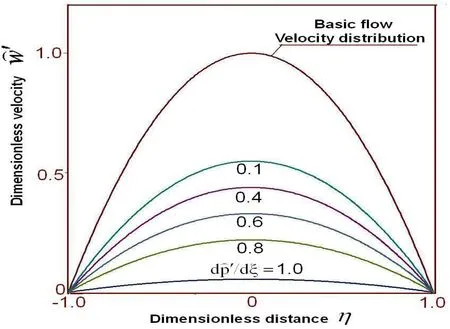
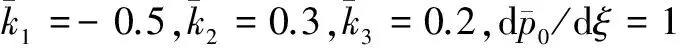
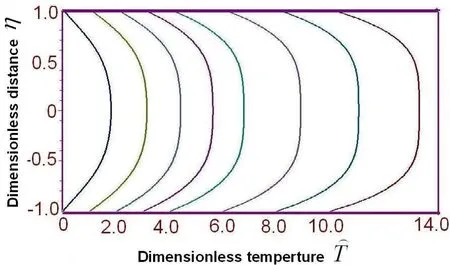
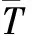
Figure 4Change of Nusselt number Nu with dimensionless distance ξ for second approximation of heat transfer theory Br=100,A0=0.4,Pr=1.0,λ1=2.51713091

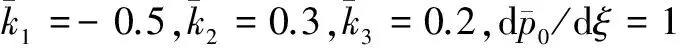
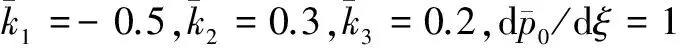
Results and Conclusions

As an important application of the developed disturbed constitutive theory the two dimensional thermal nanofluid flow between two infinite planes is investigated. The flow between two infinite planes is simulated as a flow with dominating extension, the disturbed constitutive theory has been utilized for the thermal nanofluid flow. Using the improved variational Kantorovich method and the computer software Maple 16 artificial analytical solution of the thermal nanofluid flow is obtained.

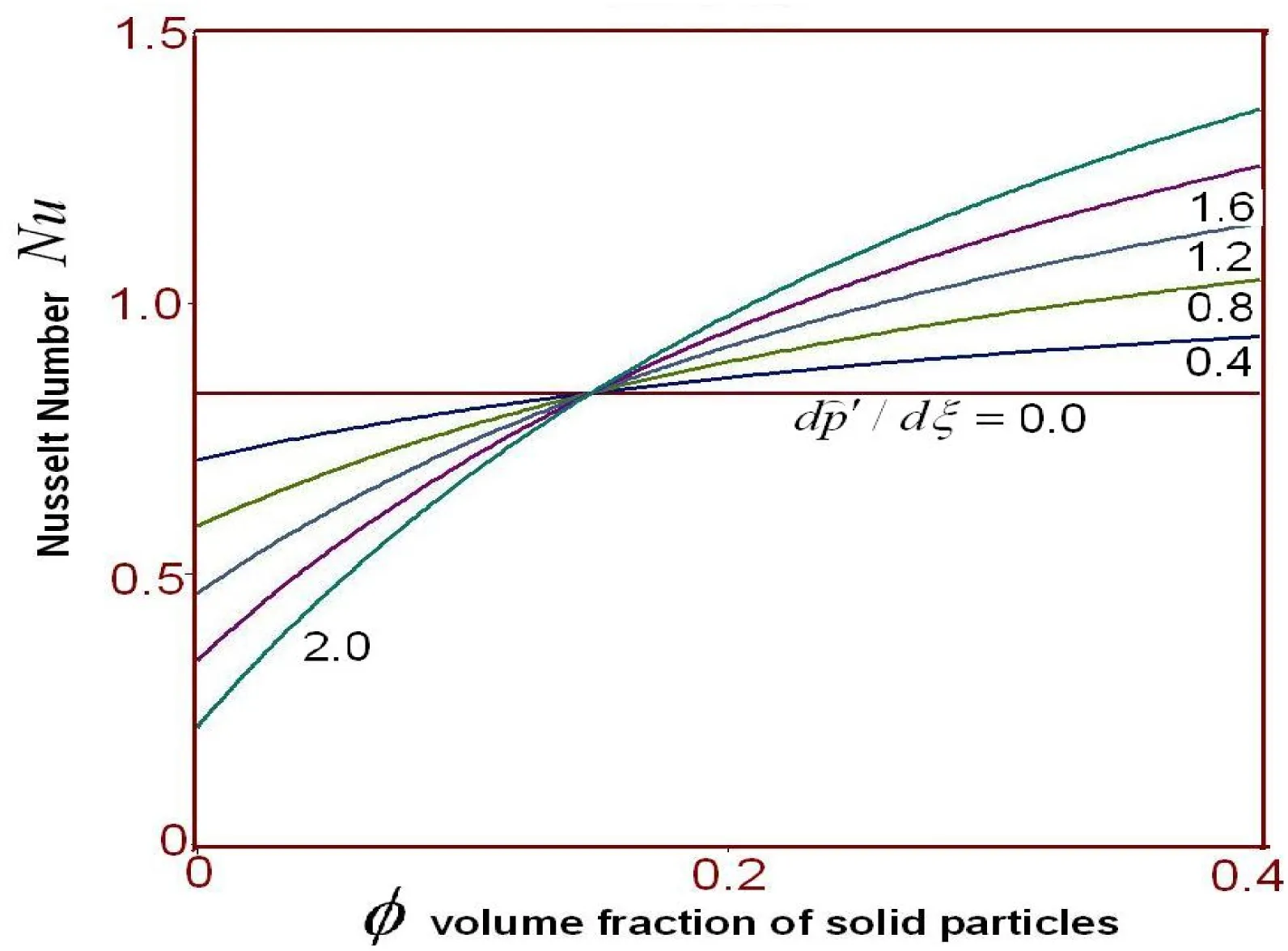
Base on the disturbed constitutive theory and using the improved Kantorovich variational approach the results of nanofluid thermal flow between two infinite planes are shown by Figs. Figure 4 shows change of Nusselt number Nu with dimensionless distance ξ for second approximation. The changes of Nusselt number Nu with volume fraction of solid particles for nanofluid flow are shown by Figs. 5 to 6 for nano-constitutive functions: Einstein model, and improved Einstein model respectively. As the experiments showed that the tendency of function Ψ(φ) is in agreement with the one phase fluid functions thereby in calculation one phase fluid models such as the Einstein , improved Einstein functions were used. It can be seen from the Figures , that The changes of Nusselt number Nu increase with the volume fraction of solid particles for nanofluid flow, it means that the suspended fine particles considerably increase the thermal conductivity of the mixture and improve the thermal capability of energy exchange equipment. The New concept non-Newtonian fluid theory, i.e. the disturbed constitutive equation theory has been successfully extended to study thermal nanofluid motion.

[1] XUAN Yimin,LI Qiang.Energy transfer theory of nano-fluid and application[M].Beijing:Science Press,2010.(in Chinese).

[2] LEE S P,CHOU S,LI S,et al.Measuring thermal conductivity of fluids containing oxide nanoparticles[J].Journal of Heat Transfer,1999,121(2):280-289.

[3] XUAN Y,LI Q.Heat transfer enhancement of nanofluids[J]. International Journal of Heat Fluid Flow 2000,21(1):158-164.

[4] HAN Shifang.Constitutive equation and computational analytical theory of Non-Newtonian Fluids[M].Beijing:Science Press,2000.(in Chinese)

[5] HAN Shifang.Continuum mechanics of anisotropic non-Newtonian fluids - Rheology of liquid crystalline polymer[M].Beijing:Science Press,2008.(in Chinese)

[6] XUAN Y,ROETZEL W.Conception for heat transfer correlation of nanofluids[J].International Journal of heat and mass transfer,2000,43(19):3701-3707.

[7] HAMAD M A A,Fenlows M.Similarity solutions to viscous flow and heat transfer of nanofluid over nonlinearly stretching sheet[J].Applied Mathematics and Mechanics,2012,33(7):868-876.

[8] AMINOSSADATI S M,CHASEMI B.Natural convection cooling of a localised heat source at the bottom of a nanofluid-filled enclosure[J].European Journal of Mechanics-B/fluids,2009,28(5):630-640.

[9] HAMAD M A A.Analytical solution of natural convection flow of a nanofluid over a linearly stretching sheet in the presence of magnetic field[J].International communications in heat and mass transfer,2011,38(4):487-492.

[10] KAVIANY M.Principle of Heat Transfer in Porous Media[M].Berlin:Springer,1995.

[11] HUILGOL R R.Nearly extensional flows[J].Journal of Non-Newtonian Fluid Mechanics,1979,5:219-231.

[12] BECKER E.Bemerkugen zur Instabilitaet der Stroemung nicht-newtonscher Fluessigkeiten[J].Zamm Journal of Applied Mathematics & Mechanics Zeitschrift Fur Angewandte Mathematik Und Mechanik,1983,63:43-48.

[13] HAN S F,BECKER E.Hydrodynamic instability of extensional flow[J].Rheologica Acta,1983,22(22):521-527.

[14] HAN Shifang.Stability of extensional flow and extending viscoelastic fluid sheets[J].Journal of Non-Newtonian Fluid Mechanics,1984,15(2):181-197.

[15] HAN Shifang.On the stability of extensional flow[J].Chemical Engineering Communications,1985,32(1):307-329.

[16] HAN Shifang.Instability of extensional flow of non-Newtonian fluid flow[J].Zeitschrift fur Angewandte Mathematik und Mechanik,1985,65(4):199-202.

[17] HAN Shifang.2008,Stability of shear-extensional flow in film extrusion of liquid crystalline polymer-anisotropic viscoelastic fluid[C]//Proc.of XVth International Congress on Rheology,California,August 3-8,2008:126-128.

[18] HAN Shifang.A stability of multiaxial extensional flow of non-Newtonian fluid sheets[C]//Proc.Ot 10th Intern. Congress on Rheology,Sydney,1988:380-382.

[19] HAN Shifang.Disturbed constitutive equation and instability of extensional flow of viscoelastic fluids[J].Acta Mechanica Sinica,1993,9(2):213-217.(in Chinese)

[20] ZAHORSKI S.Flows in converging slits and pipes as flows with dominating extensions[J].Engineering Transactions,1988,36(3)563-574.

[21] ZAHORSKI S.Axially symmetric squeezed films as viscoelastic flows with dominating extensions[J].Engineering Transactions,1986,34(1-2):181-196.

2016-03-31

国家自然科学基金资助项目(10772177;19832050 (重点))

韩式方(1935-),男，教授,湖南湘潭人,主要从事流体力学、流变学等方面的研究,(E-mail)sfh5578@sina.com

1673-1549(2016)03-0027-06

TB115

A

扰动本构方法研究非牛顿纳米流体传热流动

韩式方, 伍岳庆, 肖帆

(中国科学院成都计算机应用研究所, 成都610041)

将非牛顿流体力学理论及其方法推广应用于建立纳米流体-新概念非牛顿流体扰动本构方程，并研究其传热流动。韩式方发展了有特色的非牛顿流体扰动本构理论，并成功地应用于研究非牛顿流动稳定性,可以应用于非牛顿流动研究。将非牛顿流体扰动本构理论推广至建立新的纳米流体微扰动模型,对单相流体模型进行微扰动修正。纳米流体强化热交换机制：悬浮粒子增加二相混合体的热传导率;极细粒子随机运动，热耗散加速流体中能量转换过程。在新的纳米流体扰动本构方程基础上。研究了纳米流体传热流动，其结果表明，Nusselt 数随纳米粒子的体积分数的增加而增加，其趋势与实验结果一致，表明本理论方法是合理的，可以推广于应用一系列纳米流体流动问题。

热流体流; 新概念非牛顿流体; 扰动本构方程; 扩展流动; 计算符号处理

10.11863/j.suse.2016.03.07