焊缝不平顺对车辆-无砟轨道-路基系统振动特性的影响

裴承杰, 宋小林, 穆　玲

(1.西南交通大学牵引动力国家重点实验室, 成都　610031;2.四川川油工程技术勘察设计有限公司, 成都　610031)



焊缝不平顺对车辆-无砟轨道-路基系统振动特性的影响

裴承杰1, 宋小林1, 穆玲2

(1.西南交通大学牵引动力国家重点实验室, 成都610031;2.四川川油工程技术勘察设计有限公司, 成都610031)

基于车辆-轨道耦合动力学理论，应用有限元方法建立车辆-CRTSIII型板式无砟轨道-路基系统垂向耦合动力学模型，对高速车辆通过钢轨焊缝不平顺的动力学响应进行了仿真分析，并对比了不同形式钢轨焊缝不平顺对系统的影响。有限元计算结果表明：高速行车条件下，钢轨焊缝不平顺会引起车辆、轨道、路基系统动力学性能不同程度的变化，引起轮轨力响应增大，对与不平顺直接接触的轮对和钢轨振动产生较大影响，对行车舒适性影响有限。不同形式的焊缝不平顺对系统影响程度各有不同，凹、凸型焊缝不平顺对动力特性的影响相对接近，凹型焊缝不平顺叠加一短波不平顺后，对轮对和轨道结构振动加速度影响明显，轨道结构应力增大，受力状态恶化。在高速铁路日常运营维护中，应重视钢轨叠加焊缝不平顺引起的冲击振动作用。

车辆-轨道耦合动力学；焊缝不平顺；动力特性；有限元；CRTSIII型无砟轨道

引　言

随着我国高速铁路快速发展，高铁运营对轨道结构的平顺性提出了更高的要求。目前，我国高速铁路基本都采用无缝线路，由于焊接工艺的限制和养护维修的影响，焊接接头是无缝线路最薄弱的环节，在车辆载荷反复作用下，部分钢轨焊接接头会出现不同程度的伤损，导致钢轨磨耗不均匀，从而形成钢轨顶面焊缝不平顺。研究发现，钢轨焊缝不平顺对行车安全性和轨道结构寿命均有重要影响：一方面，焊缝不平顺会导致较大的轮轨冲击效应，引发车辆和轨道结构损伤，直接影响行车安全性；另一方面，焊缝不平顺会引起轨下基础结构振动加剧，造成基础结构累积变形，进一步降低轨道结构平顺性，增加线路的维修工作量。

针对钢轨焊缝不平顺对轮轨系统动力特性的影响，国内外学者开展了广泛的研究。Steenbergen[1]建立车轮-轨道动力学集总参数模型，研究了谐波不平顺及实测不平顺激扰下的轮轨动力响应，结果表明钢轨焊缝不平顺坡度会影响最大轮轨动态接触力。文献[2-3]通过建立车辆-轨道耦合动力学模型和钢轨焊接接头有限元模型，研究了焊缝不平顺对钢轨接头处残余应力和塑性变形的影响。杨新文[4]运用车辆-轨道耦合动力学理论、随机振动理论和声辐射理论建立了轮轨噪声预测模型，计算分析了高速列车通过钢轨焊接接头时的轮轨噪声。翟婉明[5]建立了地铁车辆-整体道床轨道垂向耦合模型，以实际测得钢轨焊接接头不平顺作为激扰输入，分析了接头不平顺引起的轮轨动力响应特征，比较了行车速度、不平顺波长和波深、轨下胶垫刚度以及轨道结构形式等对系统动力响应的影响。王慎[6]以现场实测焊缝不平顺和相应理论模型作为轮轨系统激励，对不同轴重货车的轮轨动力响应进行对比，并分析了不平顺波长和波深对不同轴重货车作用下的系统动力性能影响规律，得出波深和波长的安全阈值。目前的研究主要以单一形式的实测或理论不平顺模型为基础分析焊缝不平顺对轮轨系统的动力响应的影响，而实测线路上钢轨焊缝不平顺形式较多，有必要针对不同形式的焊缝不平顺造成的车辆-轨道-路基系统动力响应特征开展研究。鉴于CRTSIII型无砟轨道正成为我国高速铁路中主要轨道结构[7]，本文基于车辆-轨道耦合动力学理论，应用有限元方法建立车辆-CRTSIII型板式无砟轨道-路基系统垂向耦合动力学模型，对高速车辆通过钢轨焊缝不平顺的动力学响应进行了仿真分析，并对比不同钢轨焊缝不平顺形式作用下车辆轨道路基系统响应特征，为高速铁路钢轨焊缝不平顺的养护维修管理提供理论参考。

1　车辆-CRTSIII型无砟轨道-路基系统耦合动力学模型

本文借助Ansys/LS-Dyna有限元软件的前处理功能，建立了车辆-CRTSIII板式无砟轨道-路基系统模型。该模型可分为车辆系统多刚体动力学模型和无砟轨道有限元动力分析模型两个子系统，两者通过轮轨接触实现系统耦合。

1.1车辆模型

在多刚体动力学模型中，高速车辆的车体、构架、轮对等结构均按刚体考虑。高速车辆模型如图1所示，在模型中，车辆系统主要视为由1个车体、2个构架、4个轮对以及一二系悬挂系统组成的多刚体系统。车体和构架具有沉浮、点头2个自由度，轮对具有沉浮自由度。车体、构架、轮对使用Ansys/LS-Dyna中代表刚体的20号材料，悬挂系统采用离散梁单元(BEAM161)模拟。计算中车辆采用高速铁路典型动车CRH2车型，车辆运行速度为300 km/h。

图1高速车辆模型

1.2CRTSIII型板式无砟轨道-路基系统有限元模型

在有限元模型中， CRTSIII型板式无砟轨道路基系统包括钢轨、扣件、轨道板、自密实层、底座板、路基，轨道结构有限元模型如图2所示，其计算参数见表1。在对各结构进行离散时，轨道结构及路基均采用实体单元(SOLID164)模拟，钢轨、扣件系统采用梁单元(BEAM161)模拟。轨道和路基结构使用代表线弹性本构模型的1号材料，扣件所使用的材料是Ansys/LS-Dyna中具有三向刚度和阻尼的66号材料。

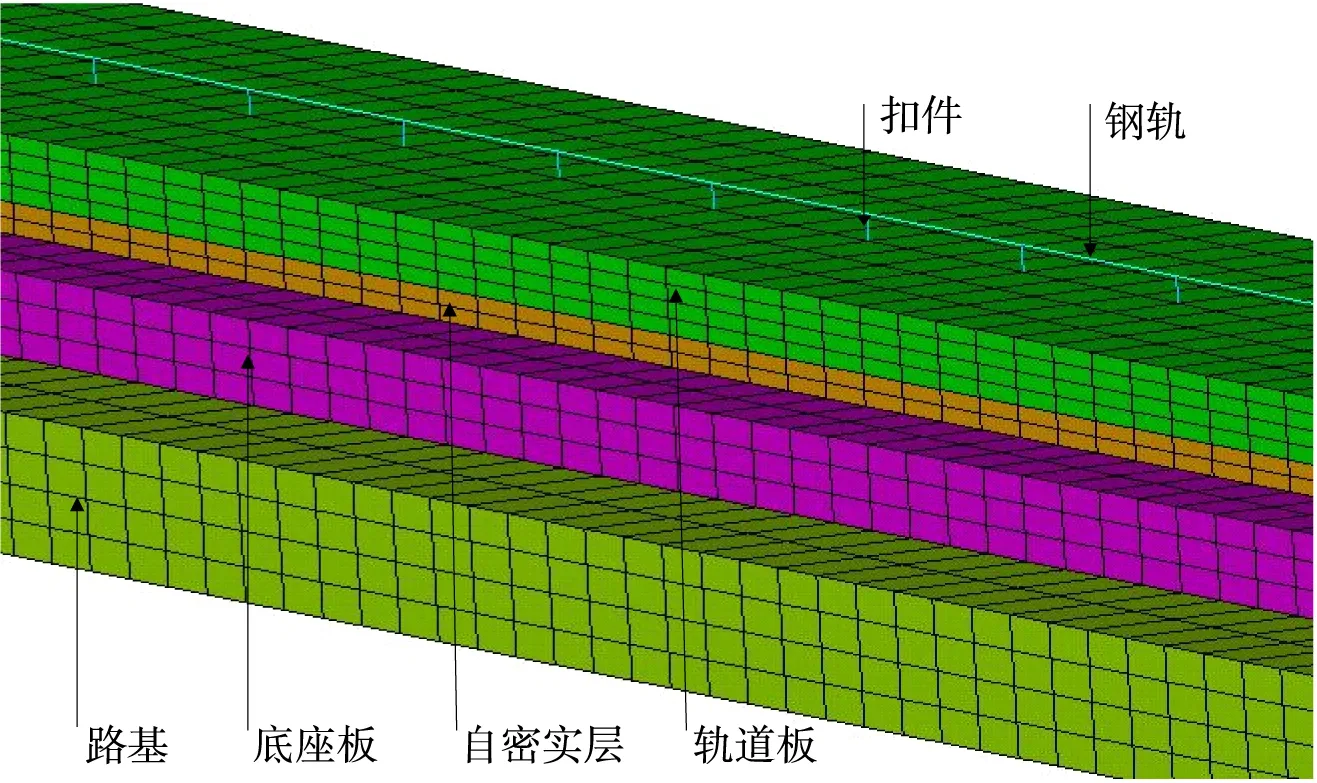
图2CRTSIII型板式无砟轨道-路基系统有限元模型

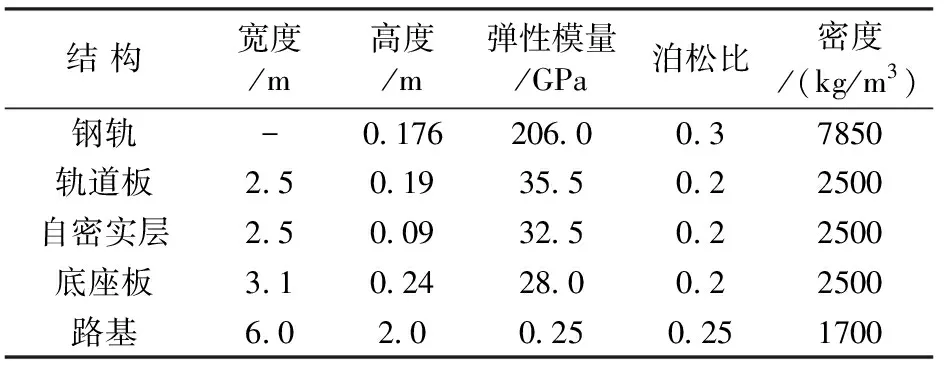
表1　轨道和路基结构计算参数

由于只考虑垂向动力特性，而且整个系统关于轨道中心线对称，因此只建立一半的车辆-轨道-路基模型，整个有限元模型共划分115 516个单元，130 868个节点。同时，不考虑轨道板、自密实层、底座板各层之间的接触面相对滑动摩擦，通过节点自由度耦合实现无砟轨道结构整体联结，底座板和路基间建立接触。

1.3轮轨关系

车辆与轨道之间的耦合作用是通过轮对与钢轨之间的耦合接触来实现的，轮轨接触力包括法向力和切向力，由于本文只考虑轮轨垂向接触，轮对与钢轨的接触可视为两弹性体之间的接触，轮轨接触力只考虑垂向力。参考国内外的轮轨接触研究资料，应用Hertz非线性弹性接触理论[8]，可确定轮轨之间的垂向接触力：

式中，G为轮轨接触常数(m/N2/3)；δZ(t)为t时刻轮轨间的弹性压缩量(m)。

1.4焊缝不平顺

钢轨焊缝不平顺是高速铁路运营过程中常见轨道不平顺激扰形式之一。目前对于焊缝不平顺一般描述为单一余弦形谐波不平顺和叠加短波不平顺[8]，余弦谐波又可分为凹、凸型两种。由于我国铁路规程对焊缝不平顺打磨的要求按焊接区长度1 m考虑，所以凹型谐波和凸型谐波数学函数均可用波长为1 m的单一余弦表示，只是不平顺方向相反。叠加短波不平顺则为1 m的凹型余弦谐波上叠加一更短谐波不平顺，如图3所示。不考虑凸型叠加短波不平顺是因为在实际的铺设和养护过程中波长较短的局部凸起一般被打磨消除了。上述三种不平顺的数学函数表达式为：

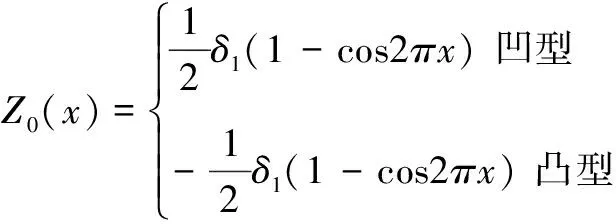
式中：Z0表示轨面不平顺幅值(mm)；x表示不平顺位置(m)；δ1、δ2分别表示长波和短波波幅(mm)；λ表示短波波长(m)。

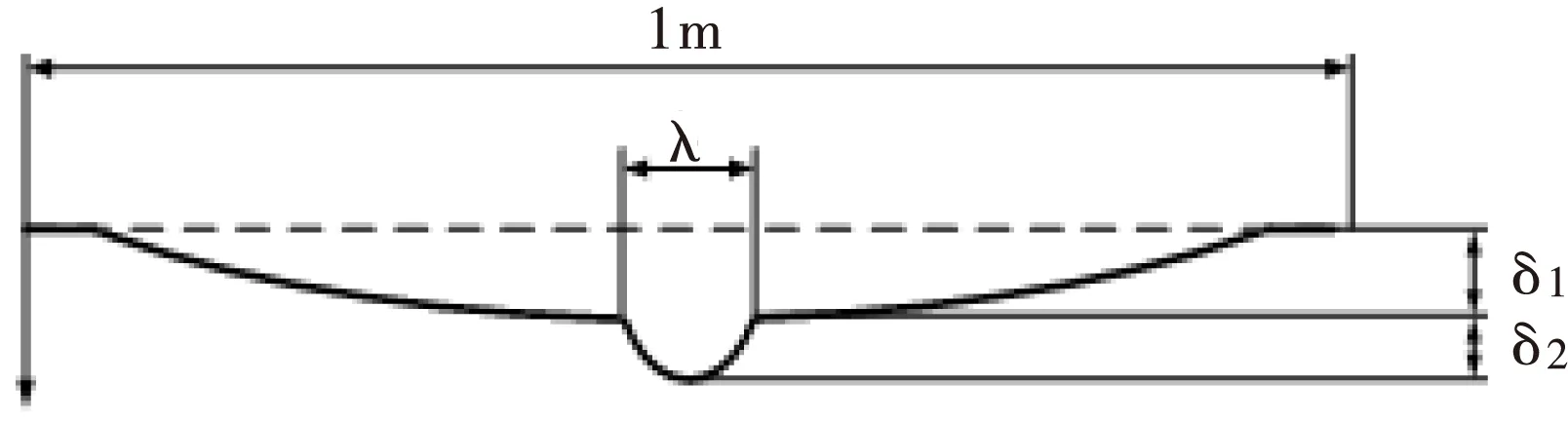
图3钢轨叠加短波焊缝不平顺

1.5模型验证

根据上节中钢轨焊缝不平顺激励模型，为了验证该模型的正确性，基于车辆-轨道耦合动力学理论[8]，运用Matlab软件编制动力学程序并对通过同一焊缝不平顺时系统的动力特性进行计算。当取叠加焊缝不平顺参数δ1=0.3 mm、δ2=0.05 mm时，两种方法计算得到的轮轨力、钢轨加速度、车体加速度时程曲线比较如图4～图6所示。

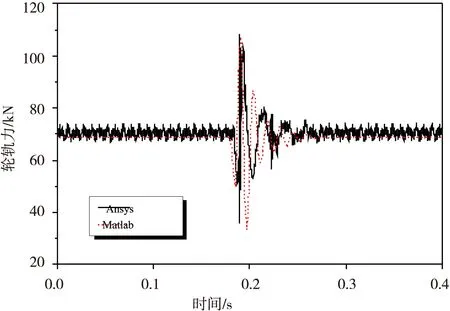
图4轮轨力时程曲线比较

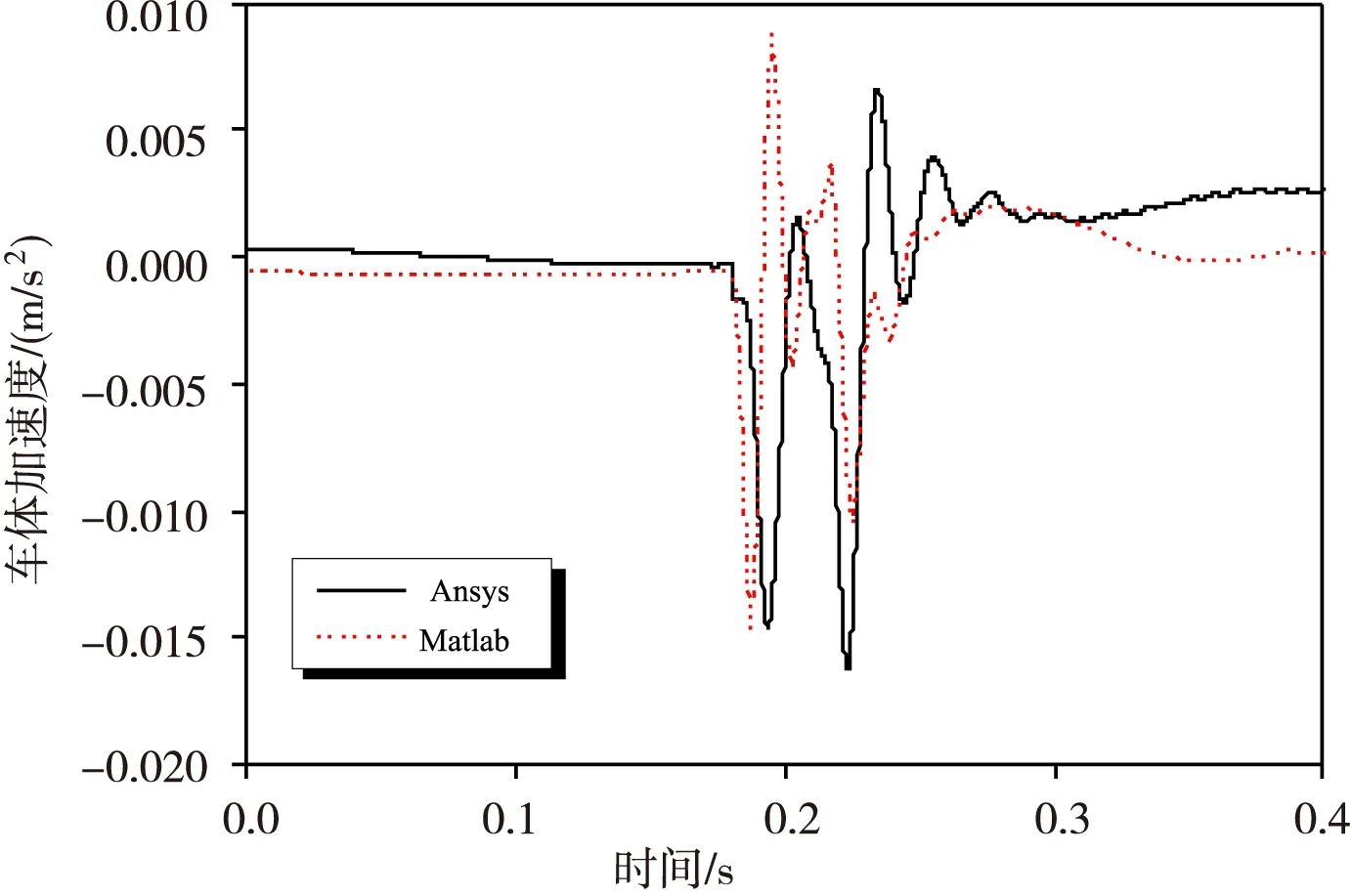
图5车体加速度时程曲线比较

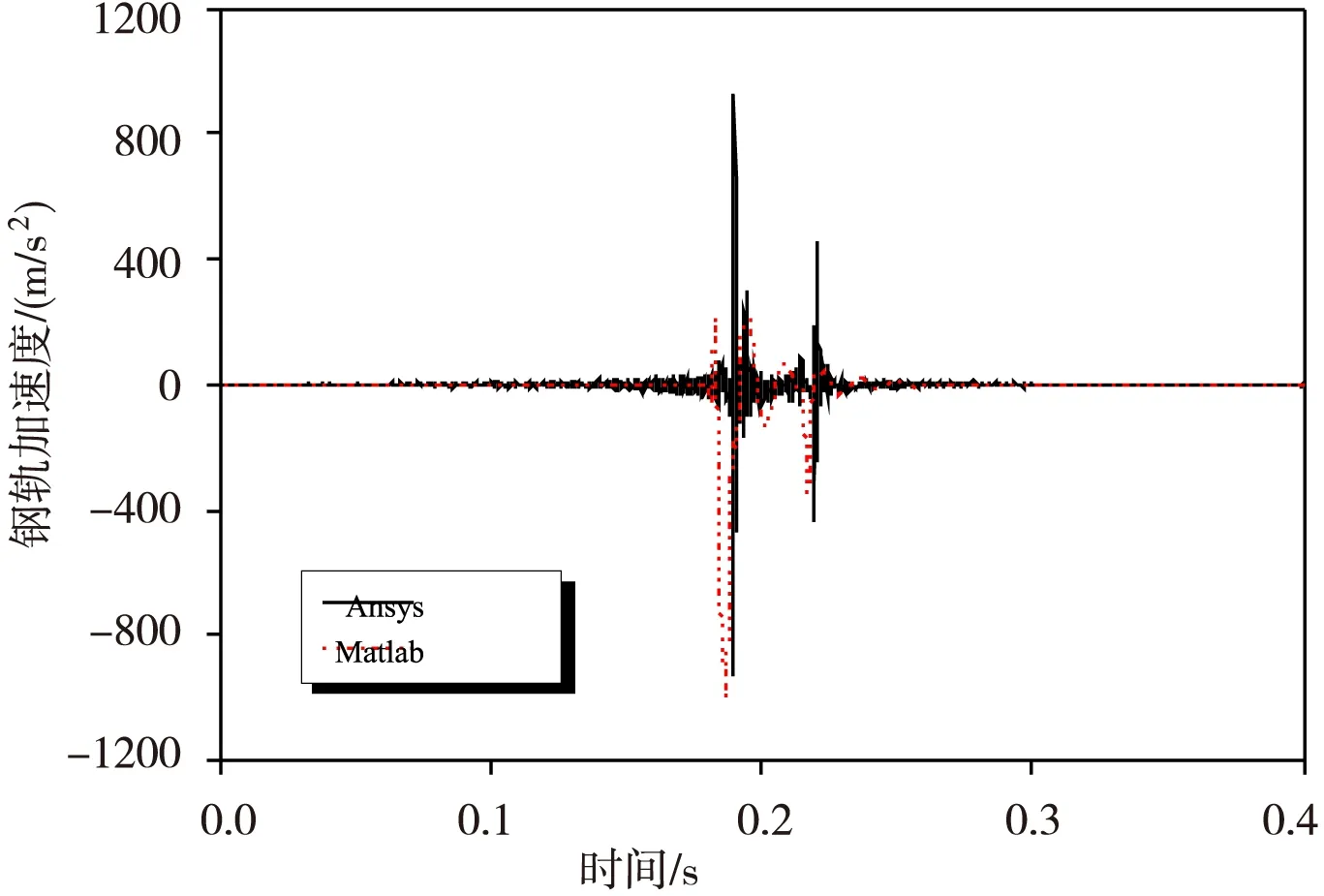
图6钢轨加速度时程曲线比较

轮轨作用力是反映系统整体动力学性能的重要指标，图4是两种方法得到的轮轨力时程曲线比较，通过Ansys和Matlab两种方法得到的轮轨力峰值分别为108.5 kN、107.3 kN，而且在整个时间范围内，两种方法得到的轮轨力时程曲线波形均取得了较好的一致性。图5和图6中车体加速度和钢轨加速度的波形也反映了加速度的主要变化规律，并且其峰值比较接近，可认为二者比较吻合。由于篇幅限制，其它一致性较好的波形不再一一列出。总体来说，有限元软件与Matlab计算结果接近，可以认为有限元模型是可靠的。

2　车辆-轨道-路基系统动力特性

2.1计算工况

本文为了分析不同形式焊缝不平顺对系统动力特性的影响，设置了4种工况：①无不平顺即理想平顺状态；②L=1 m，δ1=0.3 mm的凹型不平顺；③L=1 m，δ1=0.3 mm的凸型不平顺；④λ=1 m，δ1=0.3 mm，δ2=0.05 mm的叠加短波不平顺，具体参数及示意图见表2。

表2　焊缝类型及不平顺参数

2.2结果分析

图7是高速车辆以300 km/h速度通过理想平顺和三种不同焊缝不平顺的钢轨焊接接头时引起的轮轨垂向力时程曲线。表3是系统各结构垂向振动响应峰值统计结果，需要说明的是，该表选取的测点均为焊缝不平顺最大值所在断面。

从图7可以看出，当无不平顺时，轮轨力在静轮载(68.6 kN)附近波动；当车辆进入凹型焊缝不平顺时，由于钢轨顶面下凹，轮轨力很短时间内会产生一定的轮重减载，工况四中轮重减载率最大达到了0.49。短暂的轮重减载之后，轮对与钢轨再次冲击，轮轨力瞬间增大，通过凸型焊缝时轮轨力增至88.7 kN，凹型焊缝增幅次之，通过叠加短波焊缝增幅最大，轮轨力峰值达到了108.5 kN，该数值接近静轮载2倍。与凹型焊缝不同的是，当车辆通过凸型焊缝不平顺时，轮轨力出现先增载再减载的过程，结合表3可以看出，相比相同状态的凹型焊缝不平顺，凸型焊缝不平顺引起的轮重减载率相对较大，引起的轮轨力最大值相对较小。总的来说，通过焊缝不平顺时，轮轨力响应峰值的增大很不利于钢轨的受力，易引起钢轨接头应力增大，轨腰和轨底连接处是应力集中的区域，此处易形成材料疲劳，造成钢轨裂缝甚至导致钢轨断裂[9]。仿真计算还发现，当工况四中短波不平顺波深继续增大时，动力作用将显著增大，并可出现轮轨脱离现象(瞬时轮轨力为0)，严重影响到行车安全性。

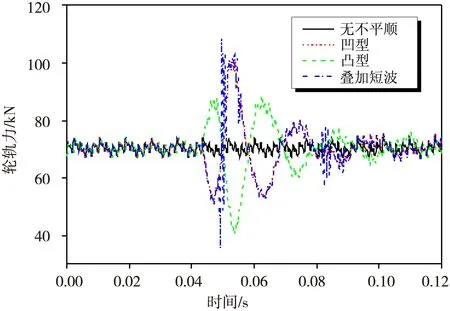
图7不同工况轮轨垂向力时程曲线对比

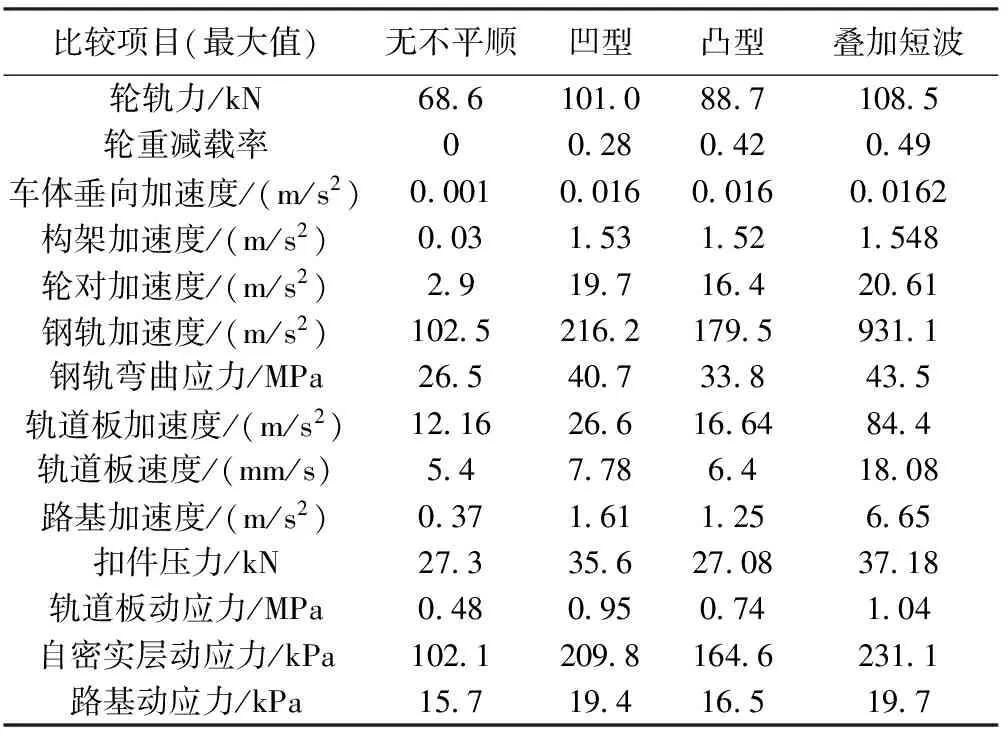
表3　不同焊缝类型计算结果对比

由表3可以看出，由于钢轨焊缝不平顺的存在，车体、构架、轮对加速度有着不同程度的反应。当车辆通过工况二焊缝区域时，车体、构架、轮对最大振动加速度分别为0.016 m/s2、1.53 m/s2、17.1 m/s2，由于车体不是与钢轨直接接触，经过转向架-二系悬挂系统良好的减振作用之后，车体和构架振动明显减弱，车体的最大加速度远低于舒适性指标0.13 g[10]，实际上，长波不平顺波深即δ1主要影响行车舒适性，而短波不平顺波深即δ2对车体的影响较小[11]。从表3还可以看出，无不平顺时轮对振动加速度在2.9 m/s2附近振荡；当车轮经过焊缝不平顺时振动非常强烈，而叠加短波不平顺对轮对的影响最大，加速度幅值达到平顺状态下的7倍，叠加一短波后，工况四相比工况二轮对加速度响应也增幅20.5%，轮轨瞬态冲击增大，这将加速轮对的损伤。

对轨道-路基系统而言，由于焊缝不平顺的存在，特别是δ2的存在，与工况二相比，工况四钢轨的振动加速度达到931.1 m/s2，增大了3倍之多，这将造成较大的轮轨噪声。轨道板和底座板加速度也有明显的增大，轨道板加速度由26.6 m/s2增大到84.4 m/s2，路基加速度由1.61 m/s2增大到6.65 m/s2，响应增幅也相当明显。

从表3可以发现，轨道结构各层受力也相应增大。当车辆荷载经过时，钢轨会发生弯曲变形，最大拉应力在轨底，无焊缝不平顺时，钢轨弯曲应力为26.5 MPa，当车辆经过凸型焊缝时，钢轨最大弯曲应力为33.8 MPa，经过凹型焊缝时，钢轨最大弯曲应力为40.7 MPa，经过叠加短波时，钢轨应力达到43.5 MPa，可见应力增幅非常明显，钢轨在这种周期性应力状态下容易产生疲劳裂纹导致钢轨断裂。另外，轨道板、自密实层、路基动应力幅值也相应增大，无不平顺时轨道板动应力为0.48 MPa，叠加短波不平顺时轨道板动应力为1.04 MPa，受力状态的恶化将影响各层结构的联结，使轨道板与自密实层产生分离，给以后的养护维修带来很大的工作量。

综合以上计算分析可知，三种不同形式钢轨焊缝不平顺的存在对轮轨冲击效应十分明显，对车辆行车舒适性的影响极小，主要影响轮对、轨道和路基结构的振动，相同幅值的凹、凸焊缝不平顺(工况二、三)对轮轨冲击的影响比较接近，凸型焊缝不平顺对系统影响相对凹型焊缝不平顺较小，凹形焊缝不平顺上叠加一短波不平顺时，轮轨冲击效应显著增大，导致与不平顺直接接触的轮对和钢轨振动明显增强，其主要原因是单一谐波不平顺幅度变化比叠加短波不平顺更平缓。叠加短波不平顺可引发轮重瞬时增、减载，过大的冲击会引起较大的环境噪声，加速轨道结构的疲劳损伤，在高速行车条件下会造成很严重的脱轨现象，影响行车安全。因此加强高速铁路钢轨的日常维护和打磨，严格限制焊缝不平顺的大小特别是防止叠加短波不平顺的存在，以降低轮轨之间的作用力是很有必要的。

3　结　论

本文在国内外研究成果的基础上，建立了车辆-CRTSIII型板式无砟轨道-路基系统垂向耦合动力学模型，并用建立的模型，对不同类型的焊缝不平顺对系统动力特性的影响进行了对比研究，结果表明：

(1) 钢轨焊缝不平顺会引起车辆、轨道、路基系统动力学性能不同程度的变化，变化比较强烈的主要是与不平顺直接接触的车辆和轨道部件，如轮对、钢轨等。

(2) 不同形式的焊缝不平顺对系统影响程度各有不同，凹、凸型焊缝不平顺对动力特性的影响相对接近，凹型焊缝不平顺叠加一短波不平顺后，系统动力特性显著增大，特别是反映整体系统动力学性能的轮轨力在进入不平顺后变化很大，轨道路基各结构部件振动剧烈，极易引起较大的轮轨噪声，轨道结构受力状态恶化，造成结构损伤。

(3) 在高速铁路日常运营维护中，应重视钢轨短波叠加焊缝不平顺引起的冲击振动作用。

[1] STEENBERGEN M J M M,ESVELD C.Relation between the geometry of rail welds and the dynamic wheel-rail response:numerical simulations for measured welds[J].Proceedings of the Institution of Mechanical Engineers,Part F:Journal of Rail and Rapid Transit,2006,220(4):409-423.

[2] WEN Zefeng,XIAO Guangwen,XIAO Xinbiao,et al.Dynamic vehicle-track interaction and plastic deformation of rail at rail welds[J].Engineering Failure Analysis,2009,16(4):1221-1237.

[3] LI Wei,XIAO Guangwen,WEN Zefeng,et al.Plastic deformation of curved rail at rail weld caused by train-track dynamic interaction[J].Wear,2011,271(1):311-318.

[4] 杨新文,翟婉明,和振兴.高速列车通过钢轨焊接接头时引起的轮轨冲击噪声的研究[J].振动与冲击,2011,30(7):143-147.

[5] 翟婉明,涂贵军,高建敏.地铁线路钢轨焊接区轮轨动力学问题[J].振动、测试与诊断,2012,32(5):701-708.

[6] 王慎.重载铁路钢轨焊缝不平顺区域的轮轨动力作用及其安全阈值分析[D].成都:西南交通大学,2014.

[7] 李阳春.武汉至咸宁城际铁路CRTSIII型板式无砟轨道技术[J].铁道工程学报,2013(4):51-55.

[8] 翟婉明.车辆-轨道耦合动力学[M].北京:科学出版社,2015.

[9] 许玉德,周宇.钢轨焊接接头最危险应力确定[J].同济大学学报:自然科学版,2003,31(2):170-173.

[10] TB10621-2014,高速铁路设计规范[S].北京:中国铁道出版社,2015.

[11] 高建敏,翟婉明.高速铁路钢轨焊接区不平顺的动力效应及其安全限值研究[J].中国科学:技术科学,2014,44(7):697-706.

Influence of Weld Irregularity on Dynamic Responses of Vehicle-track on Subgrade Vibration System

PEIChengjie1,SONGXiaolin1,MULing2

(1.State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China;2.Sichuan Chuanyou Engineering Survey and Design Co.，Ltd. , Chengdu 610031, China)

Based on vehicle-track coupled dynamics theory, a finite element model of vehicle-slab track on subgrade was developed to explore the influence of rail weld joints on dynamic responses, the dynamic response of high speed vehicle through rail welding seam was simulated and analyzed and compared the dynamic responses of different kinds of rail weld irregularity on the system, the results showed that under high speed conditions, the rail weld made the dynamic performances of the vehicle-track and subgrade system changed in different degrees and the wheel/rail force increased, great influence on the wheel and rail vibration was caused because they directly contacted with the irregularity, but the weld irregularity made little difference on comfort. Different forms of weld irregularities had different influence on the system, The influence of the concave and convex weld irregularities on the dynamic characteristics was relatively close. After concave weld uneven stacked a short wave irregularity, the influence of vibration acceleration of wheelset and track structure was more obvious, track and subgrade structure stress were all increased, and the stress state of the track structure was deteriorated. In the maintenance of high speed railway in daily operation, it was important to pay attention to impact vibration effect caused by the rail overlapping shape weld irregularity.

vehicle-track coupled dynamics; weld irregularity; dynamic characteristics; finite element; CRTS III type slab track

2016-03-31

国家重点基础研究发展计划(2013CB036200);国家自然科学基金项目(51478397；51008254);牵引动力国家重点实验室自主研究项目(2016TPL-T07)

裴承杰(1990-)，男，湖北荆州人，硕士，主要从事高速铁路技术方面的研究，(E-mail)pcj2009@vip.qq.com;

宋小林(1979-)，男，河南南阳人，副研究员，博士，主要从事高速铁路路基工程和岩石工程方面的研究，(E-mail)sxlin_2000@163.com

1673-1549(2016)03-0050-05

10.11863/j.suse.2016.03.11

TB115

A