从近几年江苏高考试题谈解析几何复习策略

周春元

(江苏省高邮市临泽中学，225621)



○高考复习研究○

从近几年江苏高考试题谈解析几何复习策略

周春元

(江苏省高邮市临泽中学，225621)

江苏近几年高考数学解析几何题一般分为两部分:一是直线与圆的方程，二是圆锥曲线．分析近几年江苏高考数学试题,将直线、圆、圆锥曲线融合在一道题中,侧重于考查学生的综合能力的试题多，主要包括求曲线(直线、圆、椭圆)方程问题及根据直线、圆、圆锥曲线求值(离心率、斜率、点到直线距离及参数取值等)．

一、高考试题题型及特点

1.考小题,重在基础

有关解析几何的小题,考查的重点在于基础知识，其中,直线与圆、圆锥曲线等内容的试题都突出了对解析几何基础知识的考查.如求直线方程,圆的方程,圆锥曲线的方程及其离心率等基础知识.

2.考大题,注重综合

平面解析几何的大题中,一般是考查直线与圆的位置关系,圆锥曲线的问题.重点考查椭圆的相关内容,考查直线与圆锥曲线之间的关系,难度属中等偏上.主要考查学生对基本知识,基本方法,基本技能的理解、掌握和应用情况，对计算能力要求较高．纵观江苏省近三年的高考试卷中解析几何题．从题型位置和分值来看，2013、2014年都是17题,分值14分;2015年18题,分值16分；从知识的考查层面看，2013年考查的是直线与圆的问题，2014、2015年考查了直线与椭圆的问题；从题量上看，三年都是两问,第一问都是基础题，第二问是中档题．

二、高考试题考查内容和方法

1.内容

(1)直线的方程；

(2)圆的方程；

(3)圆锥曲线的几何性质；

(4)直线与圆的位置关系；

(5)直线与圆锥曲线的交点.

2.方法

(1)等价转化；

(2)待定系数法.

三、解析几何复习策略教学设计

俗话说高考数学试卷解析几何是“分水岭”．解析几何做得好坏,基本就决定了高考数学的成败．因此,鉴于近几年江苏高考数学解析几何的特点．在高考解析几何复习过程中要从以下几个方面来进行复习．

1.精心研究考试说明,把握高考复习指南

如果说《数学课程标准》是数学课堂教学的基本准则,那么《考试说明》即是高三复习课的指南针．《考试说明》明确了考试内容,考试的难度，近几年的考试说明再次强调了要重视基础知识、基本技能和基本思想方法的考查．因此,高三数学教师首先应认真研读考试说明，明确命题指导思想以及分析历年来的命题方向和趋势,认真研读高考中的新动向．对出现的各种新题型有清晰的认识,并在此基础上制定详细的复习计划,针对学生的实际情况,有计划、有步骤地进行复习,做到有的放矢,这样才能提高复习的斜率．

2.分析历年高考试题，明确复习要求

解析几何是高考的重点,也是学生的难点．解析几何共有11个考点,其中3个A级考点,6个B级考点,2个C级考点．从高考看,复习中除了要注意基础知识的复习,还要搞清高考怎么考．纵观江苏省近三年及全国新课标地区试卷,一般有一个比较难的解析几何答题(一般是第二问),且所考查的内容是求轨迹问题,直线与圆锥曲线的位置关系,关于圆锥曲线的最值和定点定值问题等．其中，最重要的仍是直线与圆锥曲线的位置关系．纵观历年高考试题可以帮助教师直观地感受高考的题型,出题方式,考查知识的重点,难度要求以及在高考试卷中的位置等．

知识点要求直线的斜率与倾斜角B直线方程C直线的平行关系与垂直关系B两条直线的交点B两点间的距离,点到直线的距离B圆的标准方程与一般方程C直线与圆、圆与圆的位置关系B空间直角坐标系A中心在坐标原点的椭圆标准方程与几何性质B中心在坐标原点的双曲线标准方程与几何性质A顶点在坐标原点的抛物线标准方程与几何性质A

3.注重基本方法：基本运算能力的培养

从这三年的江苏高考解析几何试题来看，命题组在命制解析几何题目时有降低试题难度的趋势,注重通法的考查,加强运算能力考查．从2015年的解析几何可以看出高考解析几何的考查往往回归到基本方法、基本能力、基本运算的考查．所以，在复习过程中就要有的放矢，针对基本技能、基本运算能力进行训练．平时在教学过程中舍得给学生时间，要有耐心,要敢于让学生去运算，要培养学生的运算策略和运算技巧，要结合学生在训练过程中出现的问题有目的地纠错．那么，教师复习过程中要把方法选择、运算还给学生，让学生经历、体验、比较；帮助学生掌握解题的基本策略与方法.

下面介绍几种题型和基本的解决方法.

(1)求椭圆C的焦距;

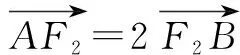
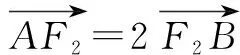
设点要反映解析几何的本质特征.

方法联立方程组

消去y,得x2+3[k(x-1)+1]2-4=0,

即x2-1+3k2(x-1)2+6k(x-1)=0.

并通过直接因式分解解此方程．

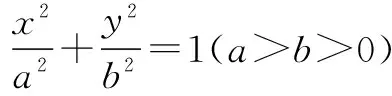
(1)求椭圆的方程;

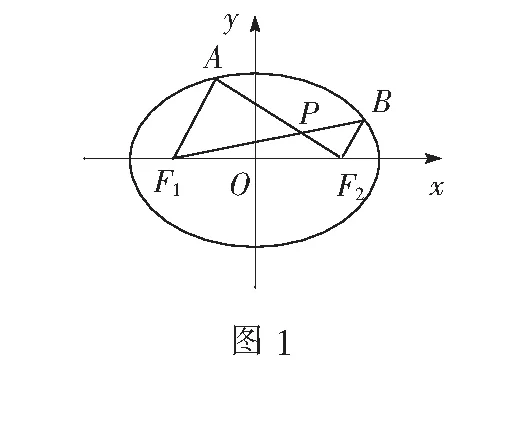
例4在平面直角坐标系xOy中,M,P是圆x2+y2=1上两个动点,点M关于x轴的对称点为N,若直线MP和直线NP与x轴分别交于点(m,0)和(n,0),问mn是否为定值?说明理由.

方法设M(x1,y1),P(x2,y2),则N(-x1,y1),且x12+y12=1,x22+y22=1.然后利用两个三点共线求出m,n，相乘即得．

4.关注学生的认知水平,找准教学着力点

“适合自己才是最好的”．教师在备课时,必须充分考虑学情,找准教学的受力点．在高三复习过程中,一定要关注学生的认知水平,特别是解析几何基础薄弱的学生,找准教学的着力点，让学生找到解决解析几何问题的信心．

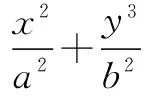
(2)若F1C⊥AB,求椭圆离心率e的值.

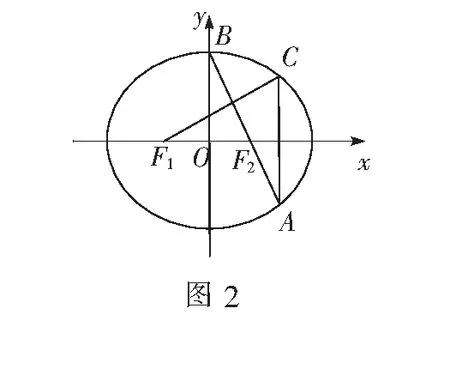
解析本题是2014年江苏高考题.主要考查学生对椭圆的标准方程与几何性质、直线与直线的位置关系等基础知识的理解与掌握,考查分析问题及运算求解能力，属中档题.

∵BF22=b2+c2=a2,

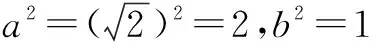
(2)设焦点F2(-c,0),F2(c,0),C(x,y).

∵点A，C关于x轴对称，∴A(x,-y)，

又B，F2,A三点共线，

①

∵F1C⊥AB,

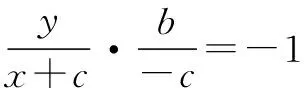
即xc-by+c2=0.

②

∵C在椭圆上，

化简得5c2=a2,

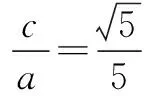
解析几何是高中数学的重点内容，对它的研究我们要关注学生的学习起点和生长点，不要好高骛远，要脚踏实地，抓住学生的实际情况，注重学生的学情，舍得花时间给学生，让学生参与到方法与运算过程中去，这样才能获得理想的复习效果.