如何提高高中数学学困生的解题能力
2016-11-04徐春花
徐春花
(江苏省吴江中学,215200)
如何提高高中数学学困生的解题能力
徐春花
(江苏省吴江中学,215200)
在数学教学中,由于学生个体学习能力的差异性,会出现一些学习困难的学生.对一个班级来说,学困生的存在不仅仅是简单的“拖后腿”,而是关系到这些学生今后的发展.对于教师来说,怎样能够有效地处理好班级学困生的关系,并使之跟得上班级整体学习的步伐,已成为教育上的社会性问题.本文就高中数学学困生学习能力提高问题,提出自己的认识与实践.
高中阶段的数学,虽然是一门基础课程,但在知识点的设置和深度上,都有了明显的提升,也就是说高中数学更注重学生思维能力的培养和训练.高中学生对数学的学习往往表现出显而易见的两极分化,喜欢的会愈发感受到数学的趣味,反之则感到数学枯燥无味,避之不及.对于数学学困生现象,教师不能放任自流,而是应该作为一项教学任务,想方设法地去帮扶这部分学生,使之数学成绩得以提高.
一、高中数学学困生形成的原因
任何年级和班级都或多或少地存在学困生问题,针对高中数学的学习来说,学困生表现出明显的消极情绪.笔者认为,学困生对数学学习的倦怠心理和缺乏自信是导致学习困难的主要原因.笔者通过长时间的分析和调查,归纳总结出导致高中数学学困生学习障碍的三大因素.
首先,缺乏数学学习的动力.不可否认的是,有的学生自小就喜欢数学,这部分学生往往逻辑思维能力较强.而对于另一部分学生来说,数学则是一门比较无趣的学科,但是由于必须要学,虽然对数学没有学习热情,但尚能跟得上学习的步伐.剩下来的一小部分学生即是本文要讨论的学困生,并不是天生就不喜欢数学,而是有经过了努力想学好却学不好的“伤心经历”,所以没有了学习数学的动力,无奈放弃.对学习数学的不自信和厌学心理,使得这部分学生对数学只能望“洋”兴叹.
其次,学困生问题表征能力弱.问题表征能力是阻碍学生学习能力提高的主要因素.问题表征能力与理解力和知识基础有关,大多数学困生都具有读题能力不足和基础知识不巩固的问题.比如,笔者发现,有的学困生会花掉很多时间来审题,却收效很差.其根源还是相关数学知识的不牢固,不具备融会贯通的能力.那些在解题中冥思苦想不得其解,而在老师的引导下才恍然大悟的学生,往往是表征能力和知识衔接遇到困难.
再次,元认知能力不强.元认知能力即是对认知的认知能力,具体来说,即是学生个体认知过程的知识以及对这些知识调用的能力.它包括元认知知识、元认知体验和元认知调节三个方面.元认知能力在数学解题中的潜在作用是通过选择有效的认知策略,达到监控认知活动具体实施的过程,并且在认知过程中,不断获取和分析反馈信息,从而正确地判断出认知策略的可行性和有效性,并在问题的解决方法和方式上进行相应的转换和改变.
当然,以上三大因素并非独立存在,学困生成绩不理想是多方面因素综合导致.就这三个因素来说,学习动力跟不上,则会导致问题表征能力薄弱,从而使元认知能力出现障碍,所以这三者是相互转化相互影响的,对学生是一个恶性循环的过程.
二、提升高中数学学困生解题能力的措施
1.留出充足的时间,培养学困生观察审题能力
在前文中已提到,学困生审题能力薄弱是导致其解题障碍的主要成因之一.基于这一点,笔者认为应首先给予学困生充分的读题时间,在教师的引导下,完成独立的审题过程.俗话说“心急吃不了热豆腐”,学困生的形成并非一朝一夕之事,所以,教师在提升学困生解题能力的教学中,亦要懂得把握“火候”.
例如,在学习勾股定理时,可借助于课本上的问题来进入讲课情境,让学生观察一枚1955年希腊发行的邮票.这枚邮票上的图案是根据著名的数学理论设计而成,教师可设计三个问题:①三个正方形面积之间有什么关系?②三个正方形的边长围成一个直角三角形,则三个正方形的面积关系怎样用边长来表示?③怎样用语言完整全面地表述问题②?
教师设计的课堂观察问题,在难度上要考虑到学困生的程度.较简单的问题可由学困生回答,并且教师要时刻注意他们在观察过程中的学习情况,作出有效的教学方案评估.注意避免直面的批评,要适当地给予引导和鼓励,只有学习数学的自信心增强了,才能有效地提升解题能力.
2.引导学生发现问题,培养其探究问题能力
长期的教育实践证明,最具有价值的学习方式是学习个体自我发现自我成长的过程.就高中数学来说,学困生对数学学习的困境集中表现就是学习方式上的困境.这部分学生往往是课堂上机械地听课,大脑思维并未随着教师的步伐而转动,没有走进数学的大门,又何谈发现数学的奥秘呢?所以培养学困生发现问题、探究问题的能力尤为重要.
仍以上文中的邮票图案解析为例,在初步审题“完美收工”后,教师指导学生运用“数学方格计算”的方式来归纳直角三角形三边关系,并实践猜想.具体步骤如下:
(1)给出的方格纸上已经画有类似于邮票图案的三组图形,通过计算小方格的个数,来算出每组图形中正方形的面积,并比较之间关系以及由三个正方形组成的直角三角形的三边关系.
(2)有的学困生提出用直尺量出三边长度,再进行面积计算,教师应给予鼓励让其动手实践.
(3)当有的学生想出割补法计算面积时,教师应给予赞赏.
不同的探究方式会得出相同的答案,教师要注意观察学困生在探究过程中的思维表现,并聆听他们的解题方法,给予指导和鼓励.
3.让学生动手操作,培养学困生手脑运用能力
数学是一门思维性很强的学科,探索发现是数学学习的动力源泉,而学困生欠缺的便是数学学习的动力.作为数学教师,要改善学困生学习数学的倦怠心理,笔者认为,可以从培养学习兴趣,鼓励探索发现多样化解题思路入手,引领学困生打开数学学习的大门.任何知识的掌握都不能仅凭死记硬背,数学更是如此.数学学习虽不是“手工活”,但在课堂上进行手工操作,亦不乏成功的教学案例.
如,在学习“边角边全等”知识点时,已知两个三角形若有两边及其中一边的对角对应相等时,那么这两个三角形是否全等?教师在讲课时,可以先让学生凭直觉判断这两个三角形是否全等,然后指导学生画出与题意相符的三角形图形,并用剪刀剪下来,对比看两个三角形是否会重合.通过实践操作得出结论,两边和它一边的对角对应相等的两个三角形不一定全等.在操作中,教师要放手给出时间,注意观察适度指导,培养学困生动手动脑能力,增强他们学习数学的自信心.
学困生问题不仅仅需要教学上的指导和改进,现实的社会现状告诉广大的教育者,对学困生心理上的疏导亦十分重要.长期的教学实践证明,造成学习成绩不能提高的主要因素便是学生的心理问题.本文主要探讨的是提升学困生学习能力所进行的教学措施,但笔者认为,教师对学困生的心理疏导应占首要,只有在学生对数学学习没有心理障碍的情况下,才能更有效地开展教学活动.
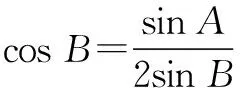
即sinA=2sinBcosB=sin 2B,
∴A=2B或A+2B=180°(舍去),
