n维球体体积公式的推导方法综述

英起志

（江苏商贸职业学院，江苏南通226011）

n维球体体积公式的推导方法综述

英起志

（江苏商贸职业学院，江苏南通226011）

该文总结和归纳了n维球体体积公式的不同推导方法，并对它们进行了分析比较。

n维；球体；体积公式；综述

引言

n维球体是n维欧式空间中一种基本的几何体，体积是它的一个基本属性。文章通过分析国内外关于n维球体体积公式的相关文献，归纳了n维球体体积公式的不同推导方法，并进行了分析和总结。

一、n维球体体积公式的推导方法

关于n维欧式空间中的球体体积的推导有不少文献，其中的推导方法不尽相同，有直接积分法、递归公式法、待定系数法、用n维球体的表面积求其体积等方法。

（一）由n维超球面的表面积求n维球的体积公式

文献［1］和［2］通过求解n维超球面的表面积公式得到n维球体的体积公式。

这一推导过程的关键在于求Sn。

（二）球面坐标下的直接积分法

文献［7］、［8］、［9］采用计算重积分的方法求n维球体的体积。广义球面坐标系包含径坐标r和角坐标φ1，φ2，…，φn-1，其中φi∈［0，π］，1≤i≤n-2，φn-1∈［0，2π］。

广义球面坐标变换公式为

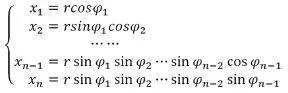
文献［5］中给出了beta函数与Gamma函数的关系：

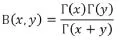
因此

（三）递归公式法

利用n维球体体积的1维和2维递归公式可以推导出n维球体的体积公式。

1.2维递归公式

文献［3］中通过n维球体体积的2维递归公式推导出体积公式，通过计算

得到

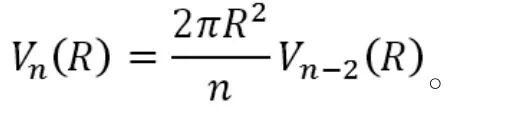
上式即为2维的递归公式。借助递归公式，结合Γ（1）=1，等事实，可以推导出n维球体的体积公式。

2.1维递归公式

推导方法与2维递归公式类似。

（四）待定系数法文献［9］、［11］中采用待定系数法推导n维球体的体积公式，其基本步骤是：先设半径为R的n维球体的体积为V（R）=aRn，其中a为常数。通过积分计算，求出a的值：

Different derivations for volume formula of N-sphere were summarized，analyzed and compared in this paper.

N-sphere；ball；volume formula；summary

O186.5

A

2096-000X（2016）21-0259-02

英起志（1983-），男，江苏连云港人，江苏商贸职业学院，数学教研室主任，讲师，硕士，研究方向为高职数学教学。