附加质量模型在拱坝自振特性分析中的应用
2016-11-03赵丽华陈丽刚杨振琨
赵丽华 陈丽刚 杨振琨
(黄河勘测规划设计有限公司,河南 郑州 450003)
·水利工程·
附加质量模型在拱坝自振特性分析中的应用
赵丽华陈丽刚杨振琨
(黄河勘测规划设计有限公司,河南 郑州450003)
基于附加质量模型的缺陷,提出了附加质量折半模型,采用该模型分析了拱坝的自振特性,并与原计算模型试验结果作了对比分析,结果表明:相对于附加质量模型,附加质量折半模型计算所得的坝体自振频率更符合实际,但偏差仍相对较大。
附加质量模型,自振特性,拱坝,模态分析
拱坝的自振特性可以通过现场原型激振试验获取,为以后的数值模拟校正材料参数,尽量减少计算中的不确定因素,对工程的安全评价具有重要的工程意义。拱坝的自振频率与水位密切相关[1],库水对坝体的作用常采用简单而实用的附加质量模型处理。以往的研究表明,附加质量模型求得的附加质量偏大,导致坝体自振频率偏低[2,3]。本文通过将附加质量折半进行坝体自振特性分析,希望获得更符合实际的坝体自振频率。
1 附加质量模型
附加质量法是一种考虑库水对坝体作用的简化计算模型,它将库水的动水压力等效成质量附加在坝体上以考虑坝体的动力响应。附加质量法并没有考虑坝体—库水动力相互作用的影响。
1933年,Westergaard在研究库水的动水压力问题时,选取垂直刚性坝面,施加水平简谐地面运动的外荷载,将库水的动水压力近似为沿水深方向呈抛物线形式分布,同时根据实测的动水压力作用在坝踵的弯矩与模拟的动水压力分布作用在坝踵的弯矩相等的条件,得出水深h处坝面的动水压力的近似公式[4]:
(1)
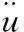
与惯性力的原理相似,用附着于结构面上的一定质量水体的惯性力代替库水的动水压力作用,由此得到Westergaard附加质量公式:
(2)
其中,Mp(h)为水深h处的库水附加质量;ρ为库水密度;h为计算点库水的水深。
Westergaard附加质量公式计算简单方便,但其适用于垂直刚性面的假设条件。1982年,Clough教授对Westergaard附加质量公式进行了修正,其能适用于任意形状的坝面,并可以考虑任意方向的地震加速度:
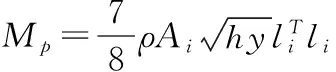
其中,li为结构面上某点i的法线矢量;Ai为该点在结构面上的控制面积。
2 拱坝自振特性分析的数值模拟
拱坝本身具有无限自由度,而自振特性的求解需要有限的自由度。有限元理论就是将具有无限自由度的空间结构体系离散成一个具有有限自由度的空间结构系统的一种近似数值算法。这样坝体就具有了有限个固有频率和振幅[5]。
不考虑阻尼和外力,n个自由度系统振动微分方程为:
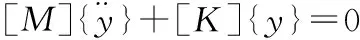
(3)

当研究库水附加质量模型对拱坝自振特性的影响时,可以忽略阻尼作用,其坝体的自由振动方程最后简化为:
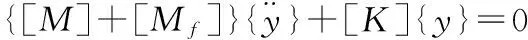
其中,[M],[Mf],[K]分别为结构的质量矩阵,附加质量矩阵和刚度矩阵。
根据微分方程组和模态分析理论,可得第k阶频率公式:
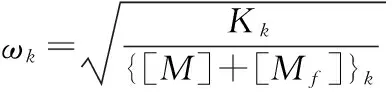
3 算例分析
3.1工程概况
某拱坝为三心圆单曲碾压混凝土拱坝,拱坝中心线与河流流向基本平行。为合理利用地形条件,改善拱坝坝体应力,在河床底部设置垫座,垫座高15 m,宽44 m。坝顶高程1 867.5 m,最低基建面高程1 735.50 m,最大坝高132.0 m,最大中心角48.90°,最小中心角16.45°,顶拱中心线弧长250.25 m,弧高比为1.90,拱冠梁顶部厚9.5 m,底部厚28 m,厚高比约0.238。
3.2计算模型
模态分析假定结构都是线性的,分析中假定混凝土、基础岩石体均为各向同性线弹性材料。计算中坝体混凝土的弹性模量取为2.51×104MPa,泊松比为0.167,密度为2 400 kg/m3。本文采用无质量地基模型模拟坝基,坝基范围取1.5倍坝高,向上下游和两侧取1.5倍坝高。基岩材料的弹性模量取为1.75×104MPa,泊松比取为0.23。库水密度取为1 000 kg/m3,未考虑水体压缩性。整个坝体离散为3 540个8节点三维等参单元,坝基离散为20 635个8节点三维等参单元,假定地基单元以外的基岩为刚性,基础全部边界节点施加法向约束。坐标原点高程1 750.0 m,位于拱坝中段圆心处。Y坐标轴为顺河流向,向上游为正方向,X坐标轴为横河向,左岸为正方向,Z坐标轴为竖直向,向上为正方向。坝体、坝基离散网格模型见图1。
3.3自振特性分析
为了与原型实验[6]结果比较,选取试验工况时的蓄水位计算。由于受试验精度等因素的影响,识别工作有时比较困难,本次仅选取前3阶自振频率进行对比。表1列举了空库、附加质量模型、附加质量折半模型和原型试验的坝体前3阶自振频率。

表1 坝体各模型下的自振频率比较表(试验水位)
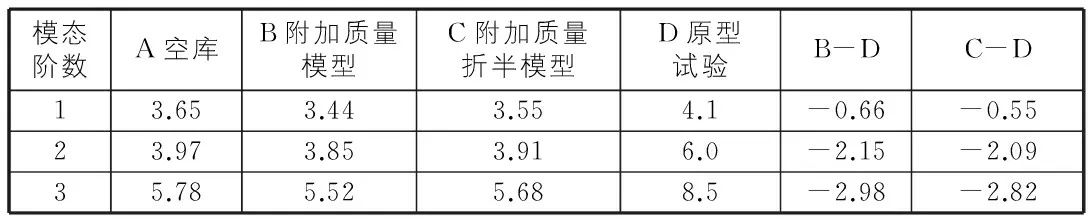
模态阶数A空库B附加质量模型C附加质量折半模型D原型试验B-DC-D13.653.443.554.1-0.66-0.5523.973.853.916.0-2.15-2.0935.785.525.688.5-2.98-2.82
通过分析可得:相对于空库情况,附加质量模型降低了坝体的自振频率,这主要是由于坝体受库水动水压力的影响。与原型试验结果相比,附加质量模型和附加质量折半模型坝体的1阶自振频率分别降低了16.1%,13.4%。相比附加质量模型,附加质量折半模型降低值相对较小,更接近原型试验结果。随着模态阶数的增加,附加质量模型和附加质量折半模型与原型试验的差值进一步扩大。由于试验是在略高于大坝运行低水位(死水位)的情况时进行的,库水附加质量模型对坝体自振频率的影响相对较小。为进一步分析附加质量模型对坝体自振频率的影响,选取正常蓄水位工况进行计算,结果见表2。

表2 坝体各模型下的自振频率比较表(正常蓄水位)
通过对比表1,表2分析可得:相对于试验时水位,正常蓄水位对坝体自振频率的影响更大。与空库计算结果相比,附加质量模型和附加质量折半模型坝体的1阶自振频率分别降低了34.5%,22.5%。可以看出,随着水库水位的增加,附加质量折半模型对拱坝自振频率的修正相对附加质量模型效果更好。
4 结语
本文提出了对库水附加质量模型进行修正的折半计算方法,与原计算模型相比,计算结果与实测结果更接近。这与文献[2]的试验结论是一致的。但结果偏差仍相对较大,如何选取更合理的修正模型需要进一步研究。
[1]寇立夯.基于性能的高坝抗震设计若干关键问题研究[D].北京:清华大学博士学位论文,2009.
[2]陈厚群,侯顺载,杨大伟.地震条件下拱坝库水相互作用的试验研究[J].水利学报,1989(7):29-39.
[3]杜成伟,柴军瑞,白峰,等.附加质量模型和坝库系统流固藕合模型的比较分析——现代水利水电工程抗震防灾研究与进展[M].北京:中国水利水电出版社,2009:338-343.
[4]Westergaard.Water pressures on dams during earthquakes[J].Trans.ASCE,1933(98):418-472.
[5]冯涛,李庆亮,孙大为.基于ANSYS的拱坝模态分析[J].河南科学,2011,29(9):1081-1084.
[6]胡晓.沙牌拱坝抗震性能计算分析报告沙牌拱坝现场试验研究报告[R].北京:中国水利水电科学研究院,2009.
Application of added mass model in the analysis of arch dam natural vibration characteristics
Zhao LihuaChen LigangYang Zhenkun
(YellowRiverEngineeringConsultingCo.,Ltd.(YREC),Zhengzhou450003,China)
Based on defects of additional quality model, the paper puts forward additional quality binary model, analyzes the arch dam self-vibration properties by applying the additional quality binary model, and makes a comparison with original calculation model. Results show that: comparing to additional quality model, the dam self-vibration frequency calculated with additional quality binary model better meets practice. However, it has larger deviation.
additional quality model, self-vibration property, arch dam, modal analysis
1009-6825(2016)19-0207-03
2016-04-28
赵丽华(1987- ),女,工程师;陈丽刚(1984- ),男,工程师;杨振琨(1986- ),男,硕士,工程师
TV311
A
