井下断层地质破碎带巷道垮落体力学特性

郝传波，　于会军，　张国华，　蒲文龙

(1.黑龙江科技大学， 哈尔滨 150022； 2.黑龙江科技大学 矿业工程学院， 哈尔滨 150022；3.黑龙江科技大学 安全工程学院， 哈尔滨 150022)



井下断层地质破碎带巷道垮落体力学特性

郝传波1，于会军2，张国华2，蒲文龙3

(1.黑龙江科技大学， 哈尔滨 150022； 2.黑龙江科技大学 矿业工程学院， 哈尔滨 150022；3.黑龙江科技大学 安全工程学院， 哈尔滨 150022)

针对断层地质破碎带巷道垮塌问题，分析了冒落堆积体边界力学特征，给出堆积体能否充满冒落空间的条件，分析充满空间和不能充满空间两种情况，推导冒落堆积体的高度边界水平抗力堆积体中任意一点的横向和纵向作用力计算公式，给出堆积体边界上的水平抗力分布曲线，堆积体中任意横向和纵向剖面上纵向作用力分布曲线。该研究可以为实施救援前预判巷道垮落体力学特性、救援时效、制定相应救援方案提供理论和技术支持。

巷道； 断层破碎带； 垮落堆积体； 力学特性

0　引　言

据煤矿事故统计和救援经验，在井下重大灾害中，第一现场瞬间死亡人员比例不到10%，其余绝大部分是因气体中毒、逃生路线阻断、氧气逐步耗尽、救援通道受阻等，使被困人员长时间得不到补给和及时救治所致[1-2]。大量井下灾后应急救援表明，如何能够安全、快速到达待援人员驻留区成为灾后能否实现有效救援的关键。

目前，从生产矿井的井下在用巷道来看，最容易导致灾后巷道垮塌并堵塞通道的地段，当属地质破碎带。如何通过在冒落堆积体中开掘救援通道，安全快速的前提是首先要弄清楚以下几个问题：一是冒落堆积体的高度如何，怎样进行确定；二是冒落堆积体与外围自行稳定岩体之间的作用力呈现何种特点，如何计算；三是冒落堆积体内块体间在横向和纵向两个方向上的作用力如何确定，存在怎样的规律。基于此，笔者研究了井下断层地质破碎带巷道垮落体的力学特性,着重从理论上进行探讨分析。

1　堆积体边界力学特征

断层破碎带内冒落岩块虽然大小不一，但是棱角并不分明，各个方向尺寸相当，下落堆积过程中呈自组织嵌合状态[3-5]。从巷道周围冒落失稳情况看，巷道顶部破碎块体冒落、两侧滑移失稳、底部松动[6-9]，最终形成椭圆形稳定迹线。在椭圆形迹线周边任何一点切向压应力大小相等，使外围围岩处于自行稳定状态，对椭圆形内部堆积体起挡护作用[10-12]。因此，地质破碎带巷道堆积体不受原岩应力场和次生应力场的影响。

由此可见，冒落堆积体属于有侧向挡护限制情况下形成的，堆积体内部的作用力源于岩块自重，在其作用下，块体在自组织嵌合堆积过程中产生相互作用。椭圆形稳定迹线外围围岩对内部堆积体的侧向作用力处于水平状态，且属于被动抗力，如图1所示。

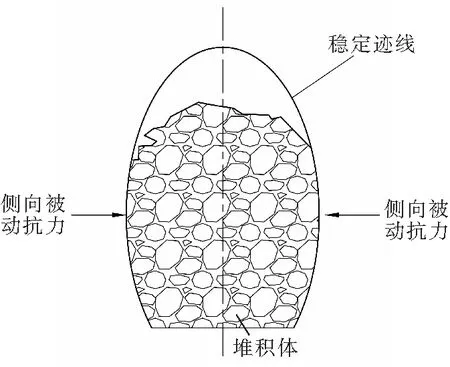
图1　冒落堆积体空间状态

2　冒落堆积体高度

冒落堆积体高度计算见图2。图2a椭圆中E1DE2G区域的面积S1为

(1)

式中：a0——巷道半宽；

a——椭圆横向半轴长度，其值为

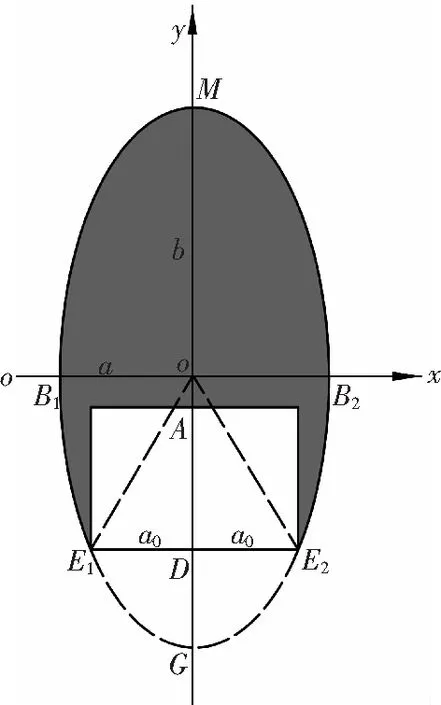
a

b

b——椭圆纵向半轴长度，其值为

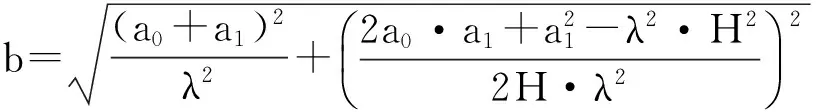
式(1)中，OD表示O点至D点的距离，其值为

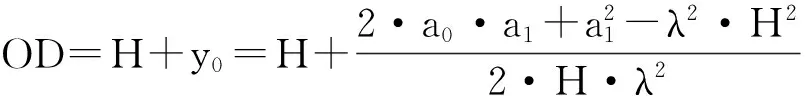
(2)

式中：λ——巷道所在断面方向上的侧向应力系数；

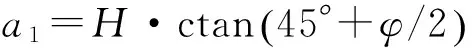
φ——块体似内摩擦角；

H——巷道的高度。

椭圆形面积St为；

St=π·a·b。

(3)

巷道断面面积Sh为：

Sh=2a0·H。

(4)

故冒落区域(阴影部分)面积Sm为：

Sm=St-Sh-S1。

(5)

断层破碎带冒落堆积体高度讨论如下：

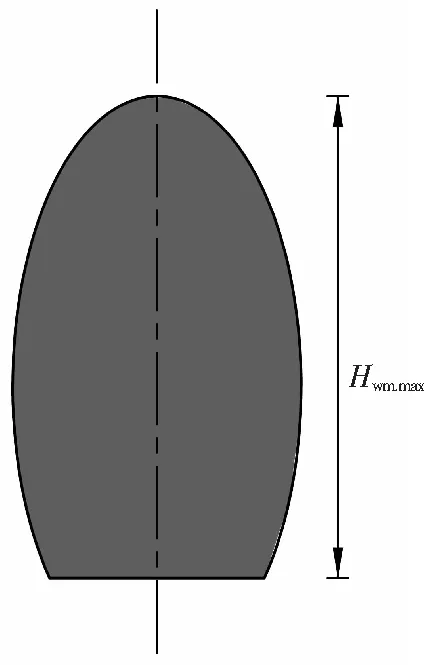
若冒落堆积体能够充满整个空间，堆积体高度：

Hwmmax=H+

(6)

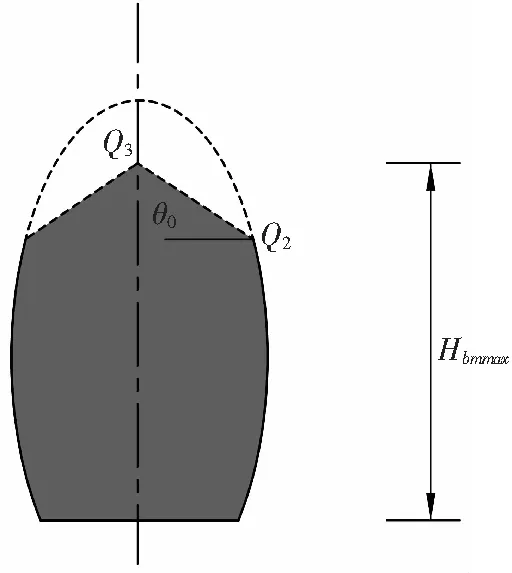
若冒落堆积体不能将整个空间充满，断层破碎带冒落堆积体两侧高度HbmQ1Q2为：

HbmQQQ2=yQ2+H+y0，即

(7)

而堆积体中部的最高高度HbmQ3为：

HbmQ3=yQ2+H+y0+x·tanθ0

式中：θ0——堆积体自然堆积角。

3　被动抗力

当冒落堆积体充满整个空间，如图3a所示，由对称性可取右半部分抗力计算，见图3b。

Q2点横向抗力R2x是MQ3Q2阴影部分堆积体沿Q3Q2迹线下滑而被动产生。将原坐标原点O向上平移到O1点，则原椭圆在新坐标系方程为

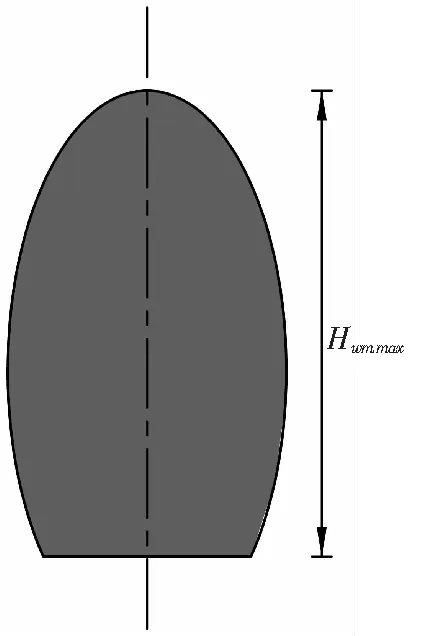
a

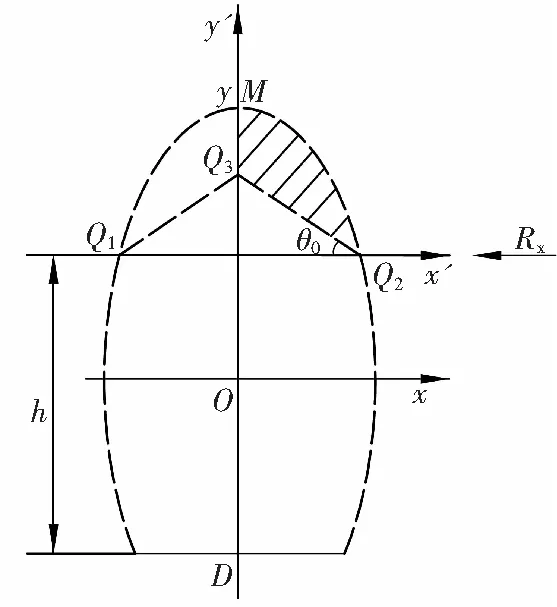
b

Fig. 3Calculationofresistancewhenaccumulationbodyfilledwithfallingspace

即在新坐标系中，椭圆满足方程：

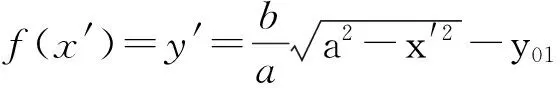
(8)

同时在新坐标系中，Q3Q2直线方程为：

f(x′)=-tanθ0·(x′-x01)。

(9)

MQ3Q2阴影部分堆积体质量为

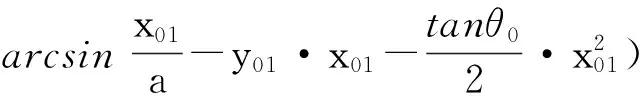
(10)

图3b阴影部分沿自然堆积角迹线Q3Q2下滑可简化为图4。

由于抗力Rx是沿Q3Q2迹线下滑堆积而被动产生，而自然堆积角θ0是在堆积下滑之后所表现出来的，故简化图中块体与斜面Q3Q2之间摩擦力为零。故有下列等式成立：

f(FMQ3Q2)=f(h，γ，a，b，θ0，a0，a1，H，λ)。

据此，抗力Rx为

f(Rx)=f(h，γ，a，b，θ0，a0，a1，H，λ)。

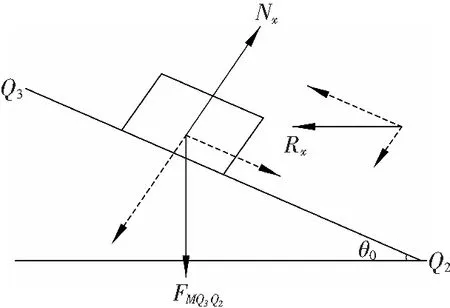
图4　堆积体充满空间抗力计算

由此可获得堆积体边界位置处抗力分布，如图5a所示，转换至直角坐标系抗力分布,如图5b所示。

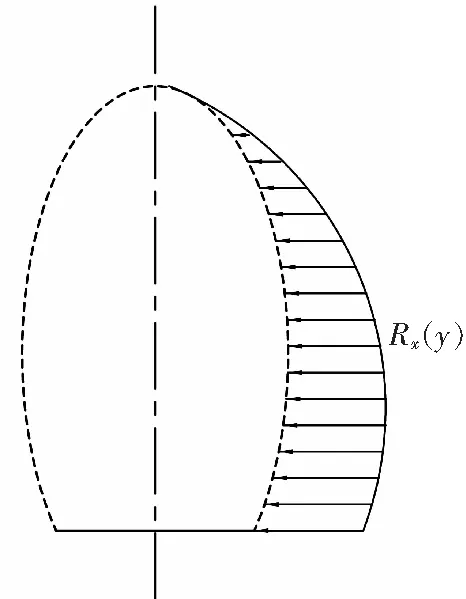
a

b

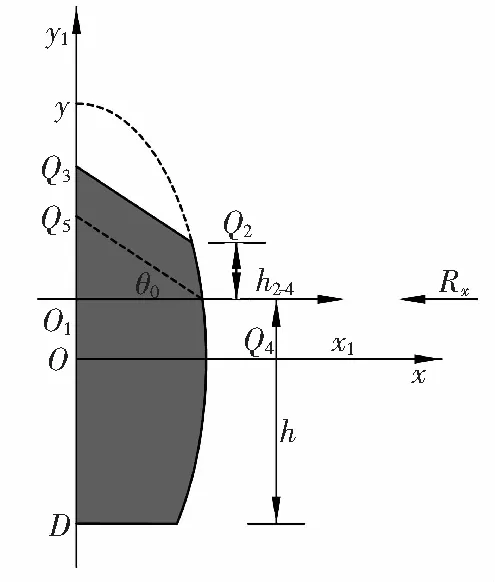
当冒落后堆积体不能充满整个空间时,见图6a，由于对称性，可取右半部分抗力计算，见图6b。

Q3Q2直线方程为

yQ3-Q2=-tanθ0·x+xQ2·tanθ0+yQ2，

Q4Q5直线方程为

yQ5-Q4=-tanθ0·x+xQ4·tanθ0+yQ4，

a

b

而Q2Q4椭圆弧段满足曲线方程：

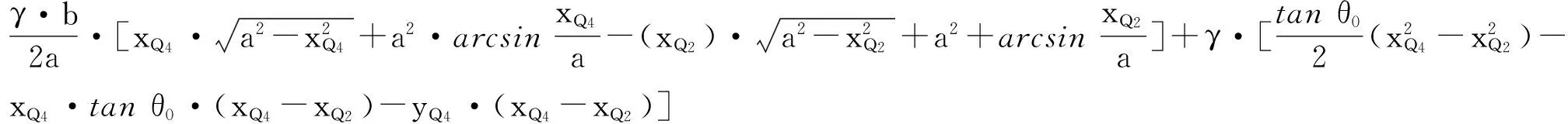
(11)

于是，图6bQ3Q2Q4Q5部分沿自然堆积角迹线Q5Q4的下滑可简化为图7。

图7　堆积体不能充满空间抗力计算

由于抗力Rx是沿Q5Q4迹线下滑堆积而被动产生的，而自然堆积角θ0是在堆积下滑之后所表现出来的，故简化图中的块体与斜面Q5Q4之间的摩擦力为零。故有下列等式成立：

Rx=FQ3Q2Q4Q5·tanθ0。

(12)

同样可获得堆积体不能充满整个空间时，在边界位置处抗力分布，如图8a所示。转换至直角坐标系抗力分布，如图8b所示。

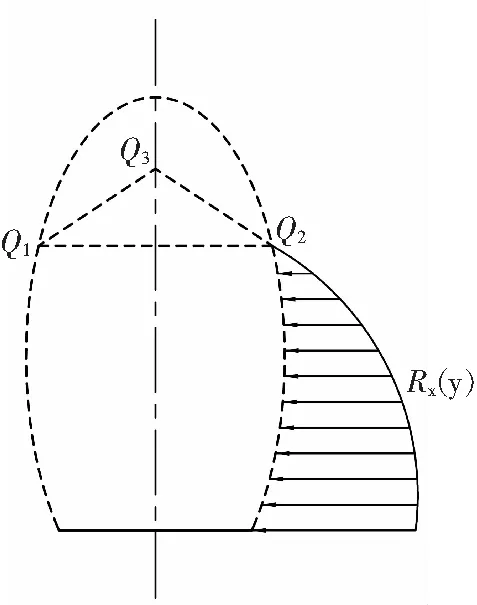
a

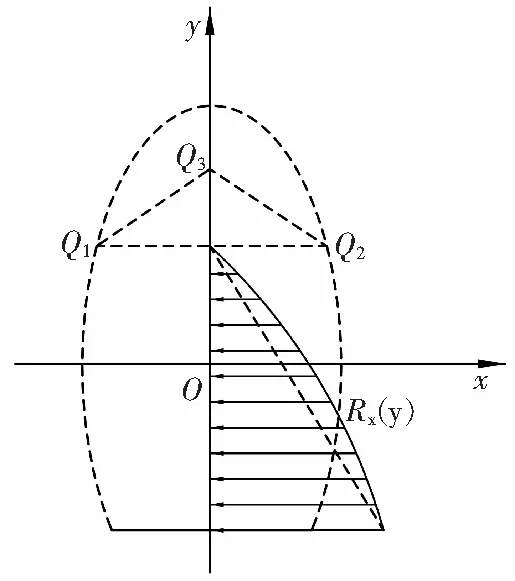
b

4　堆积体作用力

4.1横向水平作用力

通过以上分析可知，堆积体在椭圆形稳定迹线的边界位置处将受到外围围岩的抗力作用，这种抗力源于堆积体在边界位置处，沿着自然堆积角所在迹线的堆积下滑。对于堆积体内部块体之间的横向水平作用力，见图9。相应沿纵坐标方向上，不同位置处的块体间的相互作用力分布，如图10所示。

当冒落堆积体能充满整个空间时,见图3，其距离巷道底部h位置的块体作用力为：

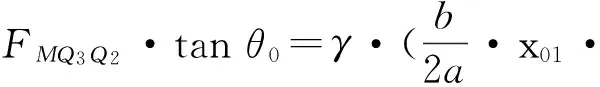
(13)式中:

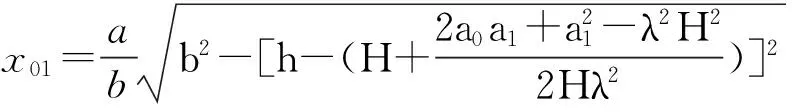
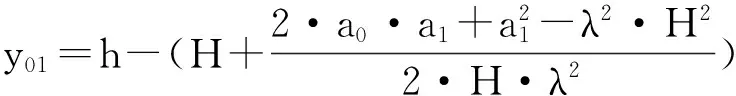
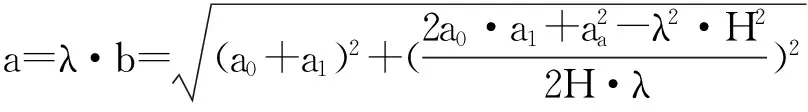
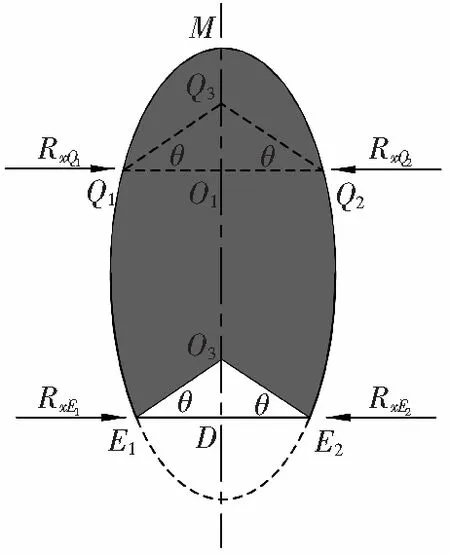
图9　堆积体内部水平作用力推算

Fig. 9Calculationofinternalhorizontalforceofaccumulationbody

图10　堆积体内块体间水平作用力分布

Fig. 10Horizontal force distribution diagram of accumulation body in vivo

当冒落堆积体不能充满整个空间时，见图6，其距离巷道底部h位置的块体作用力为：

Rx=FQ3Q2Q4Q5·tanθ0，

(14)

式中：

FQ3Q2Q4Q5=λ·xQ2·[(xQ2-xQ4)·tanθ0+

xQ4·tanθ0·(xQ4-xQ2)-yQ4·(xQ4-

xQ2)]；

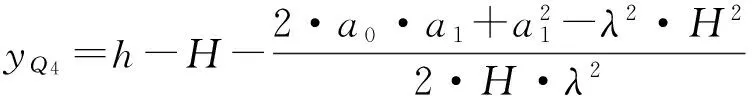
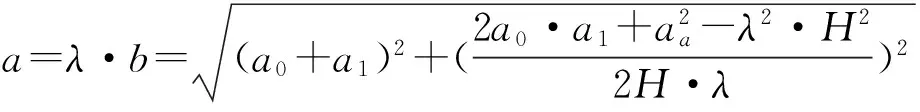
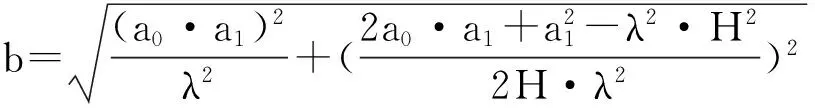
相应沿纵坐标方向上，不同位置处的块体间的相互作用力分布，如图11所示。由图11可见，在Q1Q2Q3区域因没有侧向限制，故块体间没有相互水平作用力。

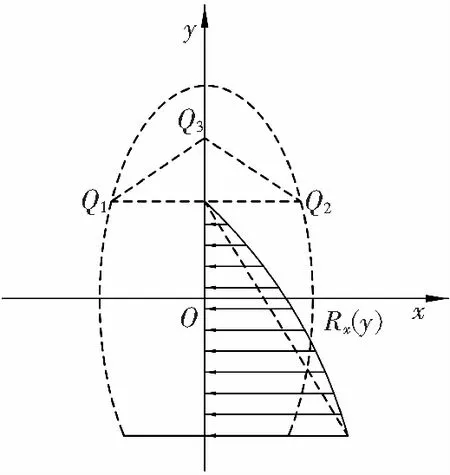
图11　堆积体内块体间水平作用力分布

Fig. 11Horizontalforcedistributiondiagramofaccumulationbodyinvivo

4.2块体纵向作用力

当冒落堆积体能充满整个空间时,如图12a。设堆积体内任意一点P，其坐标为(xP，yP)，则堆积体中P点位置处的块体间纵向应力FP为

(15)

当冒落堆积体不能充满整个空间时，如图12 b 。设堆积体内任意一点P，其坐标为(xP，yP)，则堆积体中P点位置处块体间的纵向应力FP为

FP=γ·(yP1-yP)=γ·(-tanθ0·xp+xQ2·

tanθ0+yQ2-yP)。

(16)

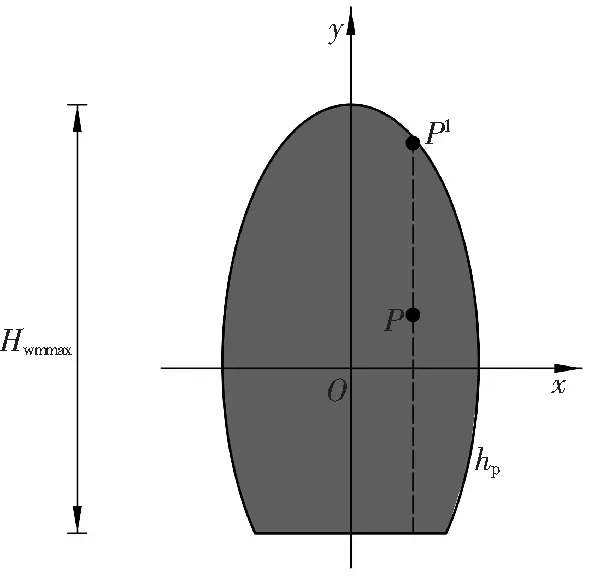
a

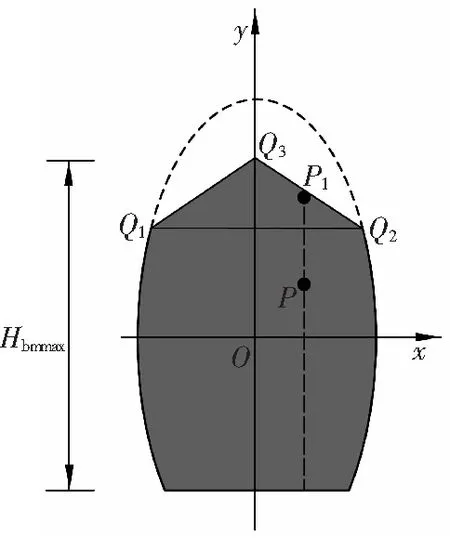
b

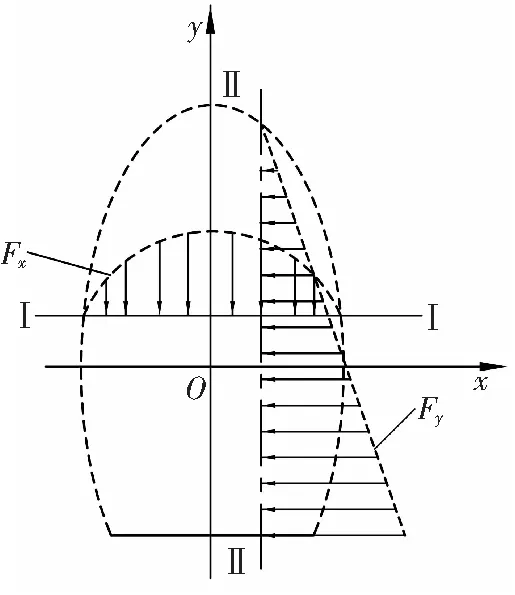
a

b

分析可知，沿纵向(图13Ⅱ—Ⅱ剖线)块体压力Fy与其所处埋深成正比关系，而在同一水平面横向(Ⅰ—Ⅰ剖线)方向上，其各点纵向压力Fx与其到堆积体上边缘的铅垂距离成正比关系。由此，可获得堆积体能充满整个空间和不能充满两种情况下，其块体纵向之间作用力分布，分别如图13a和13b所示。

5　结束语

冒落堆积体是在有侧向挡护限制的情况下形成的，堆积体内部的作用力源于岩石块体本身自重，在其作用下，才使得块体在自组织嵌合堆积过程中产生相互作用。而椭圆形稳定迹线外围围岩对内部堆积体的侧向作用力处于水平状态，且属于被动抗力。冒落堆积体是否能够将空间充填满的条件。研究中将冒落堆积体分成能够将空间充填满和不能够将空间充填满两种情况下，分别推导出了冒落堆积体的高度、边界水平抗力、堆积体中任意一点位置处的横向和纵向作用力计算公式，并给出了堆积体边界上的水平抗力分布曲线，以及堆积体中任意横向和纵向剖面上纵向作用力的分布曲线。

研究断层地质破碎带巷道堆积体力学特性，其意义在于，救援人员进驻现场实施救援前，初步判断巷道堆积堵塞巷道状态及对救援的影响，根据冒落堆积体边界特征、冒落堆积体的高度、边界水平抗力等参数，为应急救援指挥决策提供相应依据，并预判是否存在救援线路中断的可能性，为制定快速通过巷道垮塌区、判断救援时效等救援方案提供理论与技术支持。

[1]郝传波, 张国华. 顶板节理裂隙发育条件下回采巷道垮塌形态研究[J].黑龙江科技学院学报, 2013, 23(1): 28-33.

[2]郝传波, 张国华. 煤矿井下灾后救援中垮塌巷道研究的展望[J].黑龙江科技学院学报, 2012, 22(6): 549-552.

[3]徐安权, 徐卫亚, 石崇, 等. 基于数字图像的大型堆积体细观力学特性及力学参数研究[J].岩土工程学报, 2012, 34(1): 58-64.

[4]马占国, 兰天, 潘银光, 等. 饱和破碎泥岩蠕变过程中孔隙变化规律的试验研究[J].岩石力学与工程学报, 2009, 28(7): 1447-1454.

[5]马占国, 郭广礼, 陈荣华, 等. 饱和破碎岩石压实变形特性的试验研究[J].岩石力学与工程学报, 2005, 24(7): 1139-1144.[6]刘玉, 陈占清, 李顺才, 等. 饱和岩石散体蠕变行为对其力学性能影响的试验研究[J].矿业研究与开发, 2011, 31(6): 51-52.

[7]李顺才, 缪协兴, 陈占清, 等. 承压破碎岩石非Darcy渗流的渗透特性试验研究[J].工程力学, 2008, 25(4): 85-92.

[8]卜万奎. 断层内破碎岩石渗透性的实验研究[J]. 实验力学, 2012, 27(4): 469-473.

[9]苏承东, 顾明, 唐旭, 等. 煤层顶板破碎岩石压实特征的试验研究[J].岩石力学与工程学报, 2012, 31(1): 18-26.

[10]樊秀娟, 茅献彪. 破碎砂岩承压变形时间相关性试验[J]. 采矿与安全工程学报, 2007, 24(4): 486-489.

[11]孙国亮, 张丙印, 张其光, 等. 不同环境条件下堆石料变形特性的试验研究[J]. 岩土力学, 2010, 31(5): 1413-1419.

[12]李利平, 李术才, 赵勇, 等. 超大断面隧道软弱破碎围岩渐进破坏过程三维地质力学模型试验研究[J].岩石力学与工程学报, 2012, 31(3): 550-560.

(编辑徐岩)

Underground geological fault fracture zone of roadway collapse mechanical properties fall

HAOChuanbo1，YUHuijun2，ZHANGGuohua2，PUWenlong3

(1.Heilongjiang University of Science & Technology, Harbin 150022， China；2.School of Mining Engineering, Heilongjiang University of Science & Technology, Harbin 150022， China；3.School of Safety Engineering, Heilongjiang University of Science & Technology, Harbin 150022， China)

This paper is an attempt to address the geological fault fracture zone of roadway collapse problems. The research consists of analyzing the mechanical characteristics; determining the condition in which deposit caving fills up caving space, analyzing the two kinds of space namely one that can be filled up and other that cannot be filled up, inducing the horizontal and vertical force calculation formula in any point of deposit caving in height boundary horizontal resistance the of the caving deposit; giving the boundary of the deposit and the level of force distribution curve in the deposit, and the longitudinal force distribution on arbitrary transverse and longitudinal profile curve. The study may provide a theoretical and technical support to predicting the mechanical characteristics of tunnel collapse before the implementation of the rescue, rescue time, and formulating corresponding rescue plans.

roadway; fault fracture zone; deposit caving; mechanical property

2016-06-02

国家自然科学基金项目(51374097)

郝传波(1962-)，男，黑龙江省宁安人，教授，博士，研究方向：煤矿应急救援与影响控制、矿山安全与管理，E-mail：haochuanbo@126.com。

10.3969/j.issn.2095-7262.2016.04.001

TD322.4

2095-7262(2016)04-0351-07

A