基于改进ESN的时间序列数据预测及误差分析

王　悦，　付娉娉，2

(1．黑龙江科技大学 管理学院， 哈尔滨 150022； 2．哈尔滨工业大学 经济管理学院， 哈尔滨 150080)



基于改进ESN的时间序列数据预测及误差分析

王悦1，付娉娉1，2

(1．黑龙江科技大学 管理学院， 哈尔滨 150022； 2．哈尔滨工业大学 经济管理学院， 哈尔滨 150080)

为了解决时间序列数据的预测问题，传统ESN预测方法对关键参数的设置采取经验法和测试法，不能达到全局最优，因此，提出一种改进的ESN预测方法。该方法映射了关键参数的谱半径，设置优化目标，采用随机梯度下降法进行优化计算。实验结果表明，改进ESN方法的预测误差小，可以实现预测值对真实值的理想逼近。

ESN； 时间序列数据； 预测； 误差分析

0　引　言

在工业和经济领域中，不同问题间是否存在关联性和因果关系，很难直接从表面现象中获得发现。借助不同问题所对应的表征变量，分析其时间序列数据上的关联性和因果关系，往往成为最终结论的有力佐证。目前，时间序列数据的分析和预测，已经成为解决工业技术和经济管理问题的重要方法[1-2]。

时间序列数据的分析与预测，是用统计的方法将待研究问题抽象出一组时间维度上的表征数据，进而构建一个适用于这种时间序列排布的分析模型，这个模型可以用于对历史数据的分析，也可以用于对未来数据的预测[3]。在实际应用中，时间序列数据的分析与预测，也可以采用曲线拟合法加以实现。根据研究对象的历史数据拟合出一条随时间变化的曲线，可以更加直观地分析其变化规律，继而在未来时间段上进行曲线延伸，就形成了对未来数据的预测。近年来，各种时间序列数据的预测方法被提取出来，根据规划模型的不同,可以分为基于支持向量机的预测方法，基于自组织特征映射的预测方法，基于扩展卡尔曼滤波的预测方法，基于人工神经网络的预测方法[4-7]。

无论是工业技术问题还是经济管理问题，大都存在一定程度的非线性。人工神经网络的优秀性能在于，即便是非线性很严重的系统，也能找到合适的神经网络对其进行逼近。Echo State Network(状态回声网络，简称ESN)，是一种新型结构的神经网络。相比于BP等经典神经网络，ESN的迭代过程具有更好的稳定性，ESN的逼近效果更加接近最优。尤其是，ESN不会像经典神经网络方法那样陷入局部极小值[8]。此外，ESN训练过程简便快捷，更容易在复杂关系的求解上使用。

ESN方法自出现以后，在很多领域中得到了应用，但是它也存在一些问题。ESN在实际应用中，其性能优劣主要取决关键参数的配置。从现有的情况，ESN的参数配置主要依靠经验法和测试法，不仅存在效率问题还很难达到最优。为此，笔者提出改进方法，提升ESN在时间序列数据预测中的适用效果。

1　改进ESN预测方法

1.1ESN预测模型结构

从结构上看，ESN和经典神经网络一样，也包含输入层、输出层和隐含层,如图1所示。三个层次的神经元向量表达为

(1)式(1)中，I(k)代表输入层，共含有l个神经元；O(k)代表输出层，共含有m个神经元；C(k)代表隐含层，共含有n个神经元；k代表网络训练过程的迭代步进。

ESN中，输入层和隐含层之间的关系用权值矩阵Φic表示；隐含层和输出层之间的关系用权值矩阵Φco表示；输出层和隐含层之间的反馈关系用权值矩阵Φoc表示；隐含层内部各神经元之间的关系用权值矩阵Φcc来表示。ESN和经典神经网络的最大不同之处，就在于其隐含层的配置。ESN的隐含层含有规模庞大的神经元，并且这些神经元以稀疏的方式连接在一起。这使得ESN对输入-输出之间的各种复杂关系具有更强的逼近能力，并且有极大的灵活性和短时记忆功能。

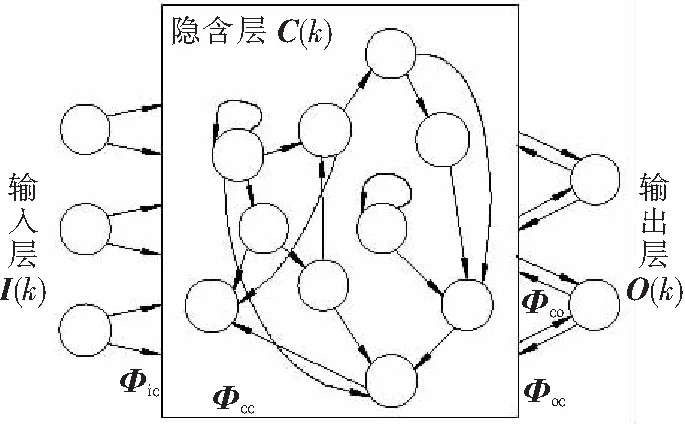
图1　ESN的网络结构

1.2ESN预测流程

设定训练ESN的过程中可以使用M个样本，包括M个输入数据样本I(k)、M个输出数据样本O(k)，那么，训练ESN的过程：

第一步，对整个ESN网络进行初始化。这一初始化工作包括对隐含层神经元向量初始化，形成C(0)；还包括对各连接矩阵进行初始化，形成Φic(0)、Φoc(0)、Φcc(0)。需要指出的是，Φco(0)最后通过计算得出，不必进行初始化。

第二步，更新迭代操作。借助输入数据样本I(k)和输出数据样本O(k)，不断迭代更新隐含层的状态C(k)，更新迭代操作如式(2)所示：

C(k+1)=f(ΦicI(k+1)+ΦccC(k)+ΦocO(K)),

(2)

式(2)中，f(·)代表了一个非线性函数，它使得ESN具有对非线性的强逼近能力。

第三步，向量数据整理。等待ESN进入平稳状态后，整理隐含层神经元向量和输入层神经元向量，从而形成状态矩阵：

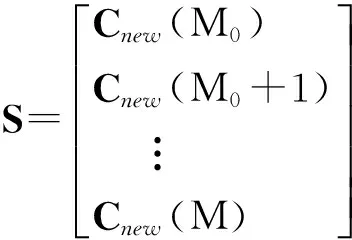
(3)式(3)中，Cnew(M)=[C(M)；I(M)]T表达了输入层神经元向量和隐含层神经元向量构成的向量对；M0代表ESN进入平稳状态后的某一个迭代步进。

同理，整理输出矩阵为

这里，T=M-M0+1。

第四步，计算连接矩阵Φco。采用矩阵的伪逆求法，计算公式为

(Φco)T=(STS)-1STD。

第五步，利用ESN完成预测。经过训练确定ESN的各个参数、连接权值矩阵之后，就可以根据输入数据对输出进行预测：

C(k)=f(ΦicI(1)+ΦccC(k-1)+ΦocO(K-1))，

O′(k)=Φco[C(k)；I(k)]，

(4)

式(4)中，O′(k)是预测结果，可以通过和实际结果O(k)的比较来计算出预测误差，进而通过误差分析来判断ESN预测效果的优劣。

1.3改进方法

根据上述流程可知，ESN预测结果的好坏与Φic、Φoc、Φcc、Φco这四个矩阵密切相关。Φic、Φoc、Φcc是先初始化再执行ESN训练得到的，而Φco是在确定Φic、Φoc、Φcc之后计算出来的。这其中，Φic、Φoc、Φcc的初始化，往往依赖于经验法和测试法。如果这些初始化的值选择的不好，会导致执行训练效率降低，同时训练出的结果很难达到最优。针对这种情况，提出两点改进措施。

1.3.1Φic、Φcc、Φoc的优化

C(k+1)=f(sicΦ′icI(k+1)+ρΦ′ccC(k)+

socΦ′ocO(k)),

Φic、Φcc、Φoc的谱半径都是1，通过sic、ρ、soc的调节，就可以形成满足谱半径要求的Φic、Φcc、Φoc。这样，Φic、Φcc、Φoc的优化问题，就转变成了对sic、ρ、soc的优化。

三个矩阵的最优配置效果，就是使得预测结果和实际结果的误差尽可能的小。为此，设定如下两个优化目标判别式：

ε(k)=O(k)-O′(k),

E(k)=‖ε(k)‖2/2。

接下来，采用随机梯度下降法来对sic、ρ、soc这三个参数进行优化，它们可以使用一个统一的公式：

p(k+1)=p(k)+η∂E(k)/∂p，

(5)

式(5)中，p可以取sic、ρ、soc这三个参数中的任意一个，η则代表更新速度。

这样，通过样本训练最终确定的Φic、Φcc、Φoc，是符合预期要求的最优结果。

1.3.2Φco的计算

Φco的最终确定，仍然采用随机梯度下降法进行计算，其迭代更新策略为

Φco(k+1)=Φco(k)+λ∂E(k)/∂Φco,

(6)

式(6)中，λ表示更新速度。因为∂E(k)/∂Φco=-ε(k)[C(k)；I(k)]T，所以式(6)可以改写为

Φco(k+1)=Φco(k)-λε(k)[C(k)；I(k)]T,

至此，Φic、Φcc、Φoc、Φco就全部确定了。相比于传统的经验法或测试法，这种改进措施确定的四个矩阵参数具有最优特性，并且对于不同的样本数据都具有较强的适应性。

2　改进ESN预测结果与误差分析

2.1实验数据

为了验证提出的改进ESN预测方法的有效性，选取两组时间序列变量数据的关系作为研究对象。一组是2005—2014年的通货膨胀率CPI月度数据，作为改进ESN方法的输入；另一组是2005—2014年的广义货币量M2月度数据，作为改进ESN方法的输出。两组数据的绝对值表达存在较大的幅度差异，因此，取两组数据的对数表达作为实验数据，如表1所示。

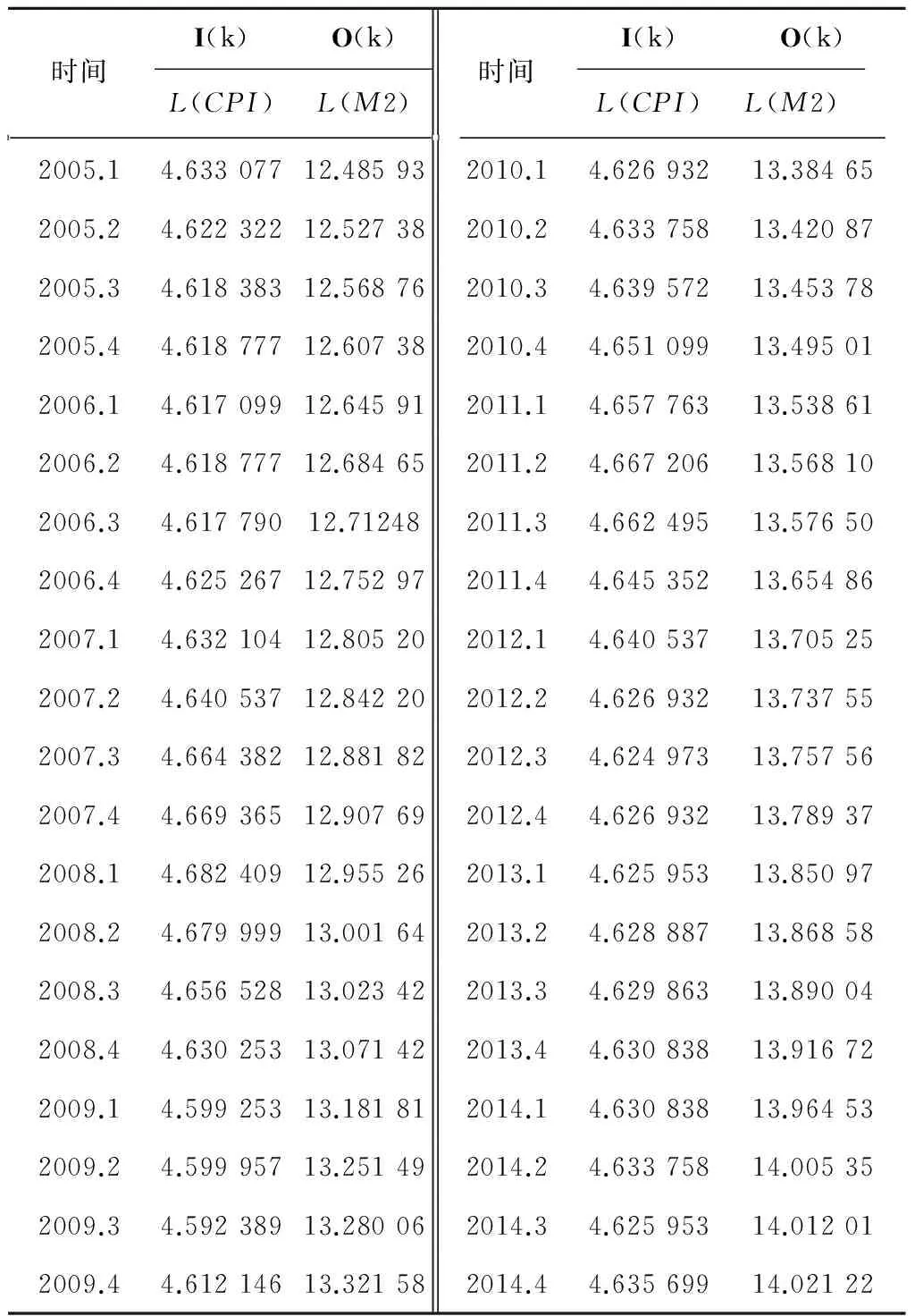
表1　实验数据

2.2预测结果

从表1的40组数据中，首先，选取20组数据对ESN进行训练，按照改进ESN方法获得ESN的各个关键矩阵参数，从而可以确定出针对此两组实验数据的最佳ESN结构。然后，将40个L(CPI)数据作为输入代入ESN，可以根据ESN获得40个L(M2)的预测值。将L(M2)的预测值和L(M2)的真实值绘制成曲线，形成的对比结果，如图2所示。

图2　L(M2)的预测值与真实值对比曲线

Fig. 2Comparison curves of L(M2) prediction values and real values

从图2中的结果可以看出，L(M2)的预测值在开始与L(M2)的真实值有很大偏差，但在ESN的逼近能力下，迅速调整到和L(M2)的真实值比较吻合的状态，并一直保持非常好的逼近效果。在40个数据以后，ESN进一步预测出未来时间范围内的20个数据，这个延伸的预测结果可以对输入和输出的未来关系问题提供统计学上的判据。图2中的结果，直观地证实了文中提出的改进ESN方法，对于时间序列数据预测的有效性。

2.3误差分析

为了形成所提出的方法和传统ESN方法的横向对比，进一步执行预测误差分析。时间序列数据的预测领域，一般通过四类误差指标来评价预测效果，即均方根误差指标、平均绝对误差指标、平均绝对百分比误差指标、标准均方根误差指标。

均方根误差指标的数学形式：

(7)

平均绝对误差指标的数学形式为

平均绝对百分比误差指标的数学形式：

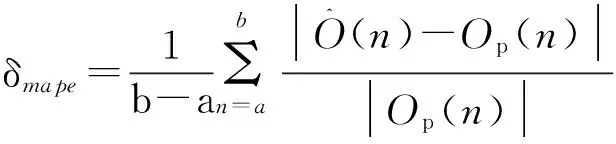
标准均方根误差指标的数学形式为

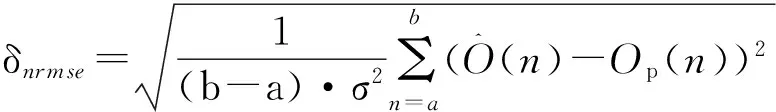
这里，σ2表示时间序列数据的方差。

根据2.1节的实验对象，分别执行传统ESN预测和提出的改进ESN预测，两种方法的预测误差比较结果如表2所示。

表2　两种方法的预测误差比较Table 2　Comparison of prediction error between two methods

从表2中的结果可以看出，改进ESN方法的预测效果要大大优于传统ESN方法，四项预测误差的评价指标都远远低于传统ESN方法。

3　结束语

改进的ESN预测方法能够获得高精度的预测结果。该方法针对时间序列数据预测问题，在传统ESN预测的基础上，对ESN的关键参数进行了优化。优化过程重新映射了关键参数的谱半径，在优化目标的引导下，采用随机梯度下降法完成优化计算。改进ESN方法避免了关键参数的经验给定和多组测试，使得ESN具有最优的逼近特性。针对时间序列数据展开实验研究，实验结果直观地证实了改进ESN方法可以获得高精度的预测结果，预测值曲线和真实值曲线的吻合程度非常高。

[1]NAND R， CHANDRA R. Reverse neuron level decomposition for cooperative neuro-evolution of feedforward networks for time series prediction[C]//Australasian Conference on Artificial Life and Computational Intelligence, Canberra, ACT, Australia: ACALCI, 2016, 9592: 171-182.

[2]刘凤朝, 孙玉涛. 我国科技政策向创新政策演变的过程、趋势与建议——基于我国289项创新城则的实证分析[J]. 中国软科学, 2007, 5: 34-42.

[3]SALEEM A, HIGUCHI K. Globalization and ICT innovation policy: absorption capacity in developing countries[C]// International Conference on Advanced Communication Technology, Pyeongchang, Korea(South): ICACT, 2014: 409-417.

[4]MINA A, BASCAVUSOGLU E, HUGHES A. Open service innovation and the firms search for external knowledge[J]. Research Policy, 2014, 43(5): 853-866.

[5]吴莎. Volterra 核函数在齿轮裂纹故障识别上的应用[J]. 河北科技大学学报, 2010, 31(6): 112-114.

[6]王永生. 基于最小二乘支持向量回归的混沌时间序列预测研究[J]. 海军航空工程学院学报, 2009,(3): 88-92.

[7]赵岚. 微分进化算法在单桩极限承载力灰色优化预测中的应用[D]. 合肥: 合肥工业大学, 2009.

[8]GUNE S, GUNDUZ O, CATATEPE Z. Link prediction using time series of neighborhood-based node similarity scores[J]. Data Mining and Knowledge Discovery, 2016, 30(1): 147-180.

(编辑徐岩)

Prediction and error analysis of time series data based on improved ESN

WANGYue1,FUPingping1，2

(1.School of Management, Heilongjiang University of Science & Technology, Harbin 150022, China;2.School of Management, Harbin Institute of Technology, Harbin 150080, China)

This paper seeks to find a solution to the forecasting of time series data and proposes an improved ESN prediction method as an alternative to the conventional ESN prediction method incapable of the global optimum due to adopting the experience method and the test method for the setting of the key parameters. This novel method mapping the spectral radius of the key parameters works by optimizing the calculation by setting the optimization goal and using the stochastic gradient descent method. The results show that the improved ESN method working with a smaller prediction error is capable of ideal approximation of prediction value to the true value.

ESN; time series data; prediction; error analysis

2016-06-01

王悦(1977-)，女，黑龙江省哈尔滨人，讲师，硕士，研究方向：管理科技术与方法、公共政策，E-mail：82265694@qq.com。

10.3969/j.issn.2095-7262.2016.04.021

TP183

2095-7262(2016)04-0458-05

A