中心支板钝化对RBCC进气道性能的影响

武乐乐，何国强，秦　飞，石　磊，张正泽

(西北工业大学 燃烧、热结构与内流场重点实验室，西安　710072)



中心支板钝化对RBCC进气道性能的影响

武乐乐，何国强，秦飞，石磊，张正泽

(西北工业大学 燃烧、热结构与内流场重点实验室，西安710072)

为了研究RBCC发动机内置中心支板钝化对进气道性能的影响，针对一变几何侧压式进气道进行了中心支板不同钝化半径下的三维数值模拟。获得了钝化半径对进气道典型工况下性能、支板抗烧蚀能力和起动特性的影响规律。数值结果表明，压升和阻力随支板钝化半径的增大而增大，出口马赫数和总压恢复系数随钝化半径的增大而减小，且来流马赫数越高，变化幅度越大；出口流场均匀度随钝化半径基本不变。钝化半径增大，进气道起动马赫数增加，中心支板抗烧蚀能力增强。

进气道；RBCC发动机；钝化；数值模拟

0　引言

火箭基组合循环(RBCC)[1-2]发动机将火箭发动机和吸气式发动机有机结合在一个流道中，有效利用火箭发动机高推重比和冲压发动机高比冲的优势，大大拓宽了飞行器的高度-速度包线。Strutjet[3]是典型的RBCC发动机之一，火箭中置是其主要特点，中心支板的作用尤为突出。支板作为进气道的一部分，可实现对来流进一步压缩，减小前体扭转角度，进而降低发动机阻力[4]，同时也有利于掺混和组织燃烧，进气道/燃烧室隔离。

在初步设计时，气动问题导致设计者将飞行器前缘、进气道唇缘和支板前缘设计得非常尖锐。从防热和工艺角度考虑，各类前缘必须钝化设计。从飞行器设计和气动力/热性能评估需求出发，国内外对压缩楔/锥前缘钝化和唇缘钝化影响的研究已有很多。国外Lewis和 Travis等对乘波体前缘钝化进行了试验[5]和数值模拟研究[6]，获得的升阻比和阻力系数与试验结果吻合较好。结果显示，气动性能随前缘钝化变化较大。Volf Borovoy[7]针对侧压进气道，研究了前体前缘、侧板前缘和唇缘钝化对进气道性能和参数分布的影响。国内周中平[8]针对不同飞行器前缘钝化半径下的高超声速二元进气道，进行了二维数值模拟，分析研究了钝化及钝化半径对高超声速进气道流动特征的影响。夏强等[9]研究了唇缘钝化半径对超声速混压式进气道稳定工作范围和工作于最大超临界状态时进气道总压恢复系数的影响。王金光等[10]研究了来流马赫数为6时前缘非对称钝化对进气道性能的影响。进气道钝化研究主要集中于飞行器前缘和进气道唇缘，而对RBCC进气道中心支板前缘的钝化研究少有涉及。

本文设计了一工作马赫数区间为1.5～7的RBCC变几何中心支板式侧压进气道，将中心支板移至隔离段内，降低进气道低马赫阻力的同时，减弱肩部分离，针对该进气道，开展了中心支板钝化半径对进气道性能影响的研究。

1　数值模拟方法

1.1物理模型和钝化方法

本文研究对象为三维侧压中心支板式RBCC进气道，图1为进气道结构示意图。该进气道设计参数为捕获面积0.04 m2；设计马赫数6.0；流量3.2 kg/s；起动马赫数低于2.5。入口宽高比为1.23，主支板占空比为0.3，总收缩比为6.35，顶压方向收缩比为4.28，侧向收缩比为1.48。为了减小进气道长度，中心支板半顶角较大，取为5.7°。该进气道为满足宽工作范围适用性要求，采用了前后移动唇口的变几何方式。构型I工作范围为Ma=1.5～2.8，唇口在位置1处；构型Ⅱ工作范围为Ma=2.8～3.5，唇口前移至位置2处；构型Ⅲ工作范围为Ma=3.5～7，唇口继续前移至位置3处。喉部宽高比为3.57，主要是为了兼顾低马赫数起动性能，隔离段宽高比越大，起动性能越好。为了提高进气道流量系数，唇口形状如图1俯视图所示，呈“V”型，主要原因是中心对称面处顶侧压激波干扰较弱，靠近侧板处，顶侧压激波干扰较强，通过将一部分压差溢流窗挡住，来提高进气道流量系数。

图1　进气道结构示意图

采用Takashima等[11]提出的作内切圆的钝化方法，如图2(a)所示，保证进气道的物理喉道面积不变。钝化前后隔离段面积变化规律如图2(b)所示，整个隔离段横截面积设计为近似等截面。其中，B表示进气道宽度，H表示喉道高度，θ1表示中心主支板半楔角，θ2表示隔离段单边扩张角，x表示距中心支板尖端的距离。

1.2计算模型和数值模拟方法验证

采用商用软件FLUENT中的有限体积方法，对进气道内外流场开展数值模拟研究。数值计算采用基于密度的隐式求解器，对流项选用Roe格式，湍流模型选用RNGk-ε模型，近壁区采用标准壁面函数法处理。计算中，使用理想气体模型，比热采用FLUENT自带的分段多项式计算模型，粘性计算采用Sutherland粘性模型。在不考虑侧滑角的情况下，进气道的几何形状和流动状态具有对称性。因此，选取进气道的1/2作为计算区域。计算中，采用了压力远场、对称面、压力出口和无滑移绝热壁面边界条件，边界条件设置如图3所示。肩部开有吸除槽，通过切换该处边界条件为壁面或压力出口，实现吸除槽的开闭。钝化支板处采用C型网格，不同钝化半径下网格数量在77.3×104～79.5×104变化，靠近壁面处网格进行加密，第一层网格距离壁面0.1 mm。

(a)钝化方法

(b)隔离段面积变化规律

以文献[12-13]中α1×α2=7°×11°模型(图4)在来流马赫数为3.95时的实验数据作为对象，对本文采用的数值方法进行校验。图5给出了壁面测压点处压强的实验测量结果和数值模拟结果。从图5可看出，沿通道底面中心线，本文的数值模拟结果与实验结果吻合很好，只是在通道后部出现较大误差。分析其原因，可能是通道后部激波/激波、激波/附面层的相互干扰给数值模拟带来一定的误差，但本文数值方法能捕捉到流场压力变化的基本趋势，整体上优于Knight的计算结果。

图3　边界条件设置及支板处网格划分

图4　α1×α2=7°×11°的模型结构[12]

图5　模型下壁面中心线静压分布

2　计算结果分析

采用上文提到的钝化方法，针对该变几何进气道，进行了中心支板前缘钝化半径为2、5、10 mm的数值模拟计算。从典型工况下性能、起动特性和中心支板抗烧蚀能力，研究钝化半径对进气道性能的影响规律。

2.1典型工况下钝化半径影响

选取了马赫数3、4、5、6、7开展了数值模拟计算，图6为典型点下进气道性能参数随来流马赫数和钝化半径的变化规律。

从图6 (a)可看出，进气道压升随钝化半径的增大而增大，且来流马赫数越高，增大幅度越大。来流马赫数为3，钝化半径10 mm时，压升仅增加了8.77%，而相同钝化半径下，来流马赫数为7时，压升增加了47.4%。从图6 (b)可看出，进气道出口马赫数随来流马赫数的增大而增大，随钝化半径的增大而减小，且来流马赫数越大，减小的幅度越大。钝化半径为10 mm，来流马赫数为3时，出口马赫数减小了0.08，来流马赫数为6时，出口马赫数减小了0.6。从图6 (c)可看出，进气道总压恢复系数随来流马赫数的增大而减小，且来流马赫数越大，减小幅度越大。来流马赫数为7，钝化半径为10 mm时，总压恢复系数仅为0.17。

(a)压升

(b)出口马赫数

(c)总压恢复系数

此时，燃烧室入口总压非常低。一般来说，进气道总压损失1%，推力大致损失1.25%，燃料消耗率提高0.3%～0.5%[14]。所以，主支板前缘应在热防护可接受范围内，选取较小的钝化半径，避免支板前缘弓形激波太强，造成太大的总压损失，降低发动机性能。

宽范围工作进气道设计难点在于高低马赫数下进气道对来流压缩程度需求不同，目前变几何进气道主要选取高马赫数为设计点，低马赫数时，通过溢流或增大喉部来实现流量匹配。选用合适的钝化半径，对高低马赫数下进气道压缩程度的提升不同，从而可缓解同一收缩比下进气道难以兼顾高低马赫数不同压缩程度需求的矛盾。进气道初步设计时，可选取较小的收缩比，采取一定的钝化半径，提高高马赫的压缩性，同时减小了低马赫阻力。在钝化方案中，R=2 mm和R=5 mm时，Ma=6进气道总压恢复系数在0.36以上；Ma=7进气道总压恢复系数在0.23以上。总压恢复系数在燃烧室可接受范围内，2种钝化方案均可采用。

图7为流场均匀度随钝化半径和来流马赫数的变化规律。流场均匀度Q计算式为Q=p/[π(λ)·σ]。其中，p、λ和σ均为出口质量流量平均值。随来流马赫数增加，进气道出口参数分布越扭曲、变化范围越来越大，Q的总体变化趋势是不断降低的。Q随钝化半径的变化基本保持不变，主要原因是虽然支板前缘弓形激波随钝化半径的增大而增强，但同时也使得隔离段内马赫数降低，抵消了弓形激波后的熵层对流场均匀度造成的影响。

图7　钝化对流场均匀度的影响

2.2钝化半径对中心支板抗烧蚀能力影响

借鉴文献[15]中数值计算过程对壁面温度的处理方法，计算钝化半径对中心支板抗烧蚀能力影响时，初始时壁面条件选用绝热壁面，计算到流场稳定。而后考虑到发动机内部许用温度为1 400 K，计算时，将壁温改为1 400 K，提取飞行马赫数为7、飞行高度为35 km时，不同钝化半径下壁面换热系数见图8。壁面换热系数h=q/(Tw-Tf)，其中q为单位面积热流量，Tw为壁面温度，Tf为流体温度。纵坐标用钝化半径为2 mm时最大壁面换热系数1 580 W/(m2·K)无量纲化。

可看出，随着钝化半径的增大，最大壁面换热系数减小。R=5 mm时，最大壁面换热系数减小了5%；R=10 mm时，最大壁面换热系数减小了17.2%；支板前缘处均为受热最严重的地方。分析其原因，支板前缘距侧压板前缘距离较远，该处流场比较均匀，不会出现横向的侧压反射激波和弓形激波的相互干扰。

图8　支板前缘壁面换热系数

假设选取中心支板材料如表1所示，取初始时刻温度为300 K，许用壁温为1 400 K，进行传热计算。图9给出了最终时刻不同钝化半径下支板温度分布。

表1　材料性能参数

R=2 mm时，3.6 s支板前缘即达到了许用温度，R=5 mm时，许用工作时间增加到8.1 s，R=10 mm时，许用工作时间增加到15.8 s。说明从热防护的角度考虑，支板前缘钝化半径应尽可能大，但钝化半径过大，会导致进气道性能的严重恶化。

具体钝化半径应从发动机工作时间要求来考虑，但钝化半径不宜超过5 mm，针对工作时间较长的发动机，应考虑主动热防护。图10给出了支板前缘温升曲线。初始时刻，温度上升速率较快，随着时间的推移，温度变化逐渐趋于平缓。

2.3钝化半径对进气道起动性能影响

针对构型I研究了中心支板钝化半径对进气道起动性能的影响，支板没有钝化时，进气道自起动马赫数为2.0，钝化半径为2、5、10 mm，对应的进气道自起动马赫数分别为2.0、2.2、2.6。

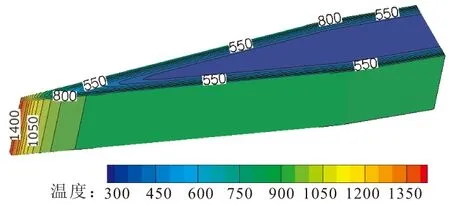
(a)R=2 mm，t=3.6 s

(b)R=5 mm，t=8.1 s

(c)R=10 mm，t=15.8 s

图10　中心支板前缘温升曲线

隔离段半高处马赫数等值线如图11所示。第2道顶压激波与侧压激波相互干扰，激波弯曲。唇口形状呈“V”型，使得内压段出现了“X”型激波的相交和反射，随着钝化半径的增大，“X”型激波和支板弓形激波干扰越严重，弓形激波引起的逆压梯度沿侧壁亚声速附面层前传，造成分离。来流马赫数为2.0，中心支板无钝化和钝化半径为2 mm时，整个隔离段通道为超声速流动，进气道起动。随着钝化半径继续增大至5 mm时，隔离段内流动阻塞，出现了亚声速流动，进气道不起动，直至来流马赫数增加至2.2时，隔离段通道出现明显的斜激波反射结构，主流保持为超声速流动，进气道起动。通过对比Ma=2.0时，R=5 mm和R=10 mm的马赫数等值线可发现，尽管进气道都处于不起动状态，但流场结构完全不同，R=5 mm时，亚声速流动出现在支板后的隔离段内，R=10 mm时，支板前端出现了亚声速流动，主要原因是钝化半径越大，弓形激波强度越大，其与跗面层的相互干扰导致气动喉道的前移，直到来流马赫数增加至2.6时，此进气道起动，主流区保持为超声速流动。

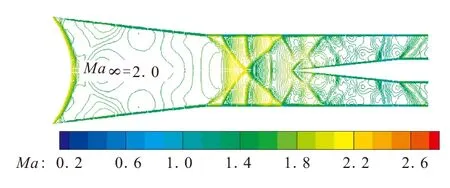
(a)无钝化

(b)R=2 mm

(c)R=5 mm

(d)R=10 mm

3　结论

(1)进气道压升和阻力均随钝化半径的增大而增大，出口马赫数和总压恢复系数随钝化半径的增大而减小。同一钝化半径下，来流马赫数越高，进气道压升增加的幅度越大，总压损失也越大。采取合适的钝化半径，对高低马赫数下进气道压缩程度的提升不同，从而可缓解同一收缩比下进气道难以兼顾高低马赫数不同压缩程度需求的矛盾。

(2)随来流马赫数增加，进气道出口参数分布越扭曲、变化范围越来越大，流场均匀度Q的总体变化趋势是不断降低的，随钝化半径的变化基本保持不变。

(3)随钝化半径增大，支板前缘壁面换热系数减小，抗烧蚀能力增加，发动机许用工作时间变长。

(4)钝化半径越大，进气道起动马赫数越高，支板前缘分离越严重。

[1]Mel Bulman,Adam Siebenhaar.The strutjet engine:exploding the myths surrounding high speed airbreathing propulsion[R].AIAA 95-2475.

[2]黄生洪,何洪庆,何国强,等.火箭基组合循环(RBCC)推进系统概念设计模型[J].推进技术，2003,24(1):1-5.

[3]Siebenhaar A,Bulman M.The strutjet engine: the overlooked option for space launch[R].AIAA 95-3124.

[4]刘晓伟.火箭基组合循环(RBCC)动力宽适用性进气道研究[D].西安：西北工业大学,2010.

[5]Gillum M J,Lewis M J.Analysis of experimental results on a mach 14 waverider with blunt leading edges[R].AIAA 96-0812.

[6]Takashima N,Lewis M J.Navier-stokes computation of a viscous optimized waverider[R].AIAA 92-0305.

[7]Volf Borovoy,Vladimir Mosharov,Vladimir Radchenko.Gas flow in a generic inlet with blunted leading edges[R].AIAA 2015-1061.

[8]周中平.钝化对高超声速进气道性能的影响[D].南京: 南京航空航天大学,2007.

[9]夏强,武晓松,孙波.钝化唇缘对超声速混压式进气道性能的影响[J].固体火箭技术,2009,32(5):514-518.

[10]王金光,张堃元.前缘非对称钝化对高超声速进气道起动性能的影响[C]//第四届高超声速科技学术会议,2011.

[11]龚鹏,岳连捷.带中心支板侧压进气道流场特性研究[J].实验流体力学，2008,22(1): 31-35.

[12]Knight D,Garrison T,Settles G,et al.Asymmetric crossing shock wave/ turbulent boundary layer interaction[R].AIAA 95-0231.

[13]Zha G,Knight D.Computation of 3D asymmetric crossing shock wave/turbulent boundary layer interaction using a full Reynolds stress equation[R].AIAA 96-0040.

[14]廉筱纯,吴虎.航空发动机原理[M].西安：西北工业大学出版社,2005.

[15]袁双,李强,秦飞,等.RBCC发动机亚燃模态热环境分析[J].科学技术与工程,2012,12(5):1085-1089.

(编辑：崔贤彬)

Influence of blunted central strut on performance of RBCC inlet

WU Le-le,HE Guo-qiang,QIN Fei,SHI Lei,ZHANG Zheng-ze

(Science and Technology on Combustion,Internal Flow and Thermal-Structure Laboratory, Northwestern Polytechnical University，Xi'an710072，China)

In order to investigate the influence of blunted central strut on the performance of RBCC inlet,numerical simulation was carried out based on a variable-geometry sidewall compression inlet.The influence of different blunt radius of central strut on the performance parameters was studied. The results show that,with the blunt ratio increasing,pressure ratio and drag coefficient increase, the Mach number at the exit of the inlet and pressure recovery decrease.The higher free stream Mach number, the greater the change.Bluntness radius has little influence on the uniformity of the flow field at the exit of the inlet. Along with the increase of bluntness radius,the starting Mach number increases and central strut erosion capacity enhances.

inlet;RBCC engine;bluntness;numerical simulation

2015-06-24；

2015-08-04。

武乐乐(1992—)，女，硕士生，研究方向为航空宇航推进理论与工程。E-mail：wulele@mail.nwpu.edu.cn

V211.48

A

1006-2793(2016)05-0606-06

10.7673/j.issn.1006-2793.2016.05.002