数学助破凶案的奥秘之二

陆继宗?隽武

陆继宗

上海师范大学物理系教授（已退休）。曾任物理系系主任，上海物理学会副理事长。

美国曾拍了一部别出心裁的侦破系列剧，名为《Numbers》，直译意思为“一些数字”，中文意译为《数字追凶》。剧中有两个主要人物，一为联邦调查局特工丹·埃普斯，一为他的弟弟——数学家查利。每一集都围绕查利如何用他掌握的数学知识和数学工具来帮助哥哥破获刑事凶案，使数学成为协助破案的利器。《数字追凶》第一季第五集《首要嫌疑人》讲述的是一起有关编码解码的数学理论的绑架案。

绑架小女孩疑案

在这集电视剧中，一对父母为他们五岁大的女儿庆祝生日时，小女孩被绑架了。正当丹和他的同事们到女孩家了解情况时，她的父亲接了一个电话后，突然表示不希望丹和他的联邦调查局团队介入这个绑架案。

小女孩被绑架

丹感到事有蹊跷，而且又发现这个女孩的父亲依桑是一名数学家，于是他就请求查利帮助调查。到女孩家中，查利看到一块白板上有一些数学式，是依桑随手写下的。查利知道这是数学上著名的黎曼猜想的式子，这说明依桑正在研究黎曼猜想。

黎曼猜想是一个世界著名数学难题，150多年来一直未被破解，以致在2000年被列为千禧年问题之一。所谓千禧年问题，是时值世纪之交的2000年，由国际著名数学家组成的一个专家小组列出的7个尚未解决的数学问题，并且悬赏100万美元征求解法。任何人只要破解其中的一题，就能得此巨额奖金。其实，破解黎曼猜想不仅可以声名大振并获得巨额奖金，更为重要的是还能得到一个破解加密系统密码的方法。

当丹从种种蛛丝马迹中确定了绑架者之一的身份，并了解到绑架者并非索要赎金，他们的计划是“破解世界上最大的金融秘密”，绑架依桑女儿的目的就很清楚了——绑架者就是想得到依桑解决黎曼难题的方法，利用它去入侵美国联邦储备委员会的计算机网站，获取诸如何时加息等极其重要的核心机密，从而能获得几百万美元甚至更高的收益。丹决定让依桑向这帮家伙提供他的研究结论，从而让他们能够进入美联储网站（其实是丹他们伪造的），以便丹的团队同时进行电子跟踪，抓住这些窃贼。查利发现在依桑的解决方案中有一个重要错误，其实依桑并未真正解决黎曼难题。于是，丹设计了一个具体的方案，即一个愚弄绑架者的方法：一方面设置一个假的美联储网站，另一方面让依桑提供一个窃贼们所要求的互联网解密的假密钥，由此追踪到他们的所在位置以解救依桑女儿。

查利看到一块白板上有一些数学式

为了破案的需要，查利给联邦调查局的特工们讲解了互联网的加密原理。现在主要的加密方法是利用大数分解成素数的难度（这在后面会作简单介绍）。众所周知，由两个已知的素数得到它们的乘积（合数）是很容易的，不论这两个素数有多大，把它们相乘就可以得到乘积。但是反过来——即把此乘积分解为两个素数——却异常困难。现在的加密系统就是利用这个特性进行加密的。解密过程就是从一个乘积寻找出两个素数因子。在这个故事中，查利和依桑一起将依桑的解法转变成了一个算法，并把这个算法提供给了绑架者，让他们利用这个算法得到密钥。查利断定绑架者们不会拥有超级计算机，他们只能将许多台PC机连起来，构成一台超级计算机来运算此算法，才能得到破解网站的密钥。由于多台PC机同时运转会散发大量热量，窃贼们就需要买多台空调机散热，而且至少需要运行好几个小时。这样一来，不但使得丹的团队有了侦查的目标——多台空调机，还为他们争取了时间。最后，按照这个方案，联邦调查局果然引诱窃贼上钩，将他们一网打尽，顺利地解救了被掳去作为人质的小女孩。

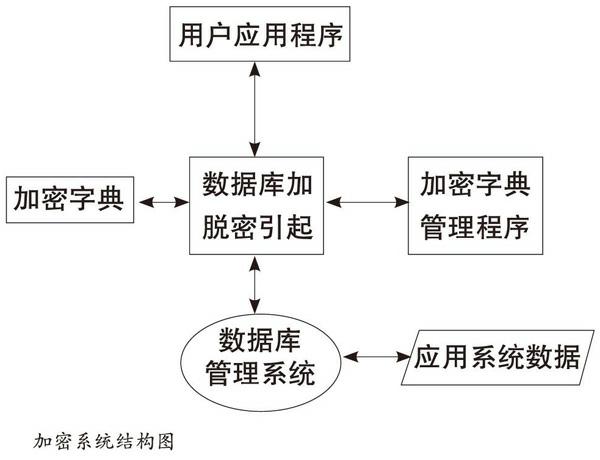
如何遏制网络犯罪？

像通常那样，《数字追凶》剧中的陈述都是在数学上有意义的，也有真实背景的故事。本集的基本前提是：黎曼问题的一个解，非常可能会导致现在所用的保持互联网秘密的方法崩溃。

现在偷钱并不需要枪和刀，一台廉价的PC机和互联网的一个连接就能偷走大量的钱。这叫做网络犯罪，是一种新的犯罪方式，不仅案例多，而且还在日益增长。它包括范围广泛的非法活动：诸如软件盗版、音乐盗版、（多种形式的）信用卡诈骗、身份诈骗、股票操纵、公司间谍以及“钓鱼网站”（假冒从一个金融机构给计算机用户发送电子邮件，目的是使收件人泄露他们的银行信息和其他个人资料）等。我们中国屡屡发生的金融诈骗事件，从广义上说也是网络犯罪。

关于网络犯罪的猖獗程度，尚无可靠的数据，因为许多银行和互联网商务公司对这样的信息往往三缄其口，以避免造成你的金钱或信用卡号码在他们手中不安全的印象。已有估计认为，网络犯罪一年的收益在1，000亿美元以上。如果这是真实的，它将超过世界上非法毒品销售的收益。不管实际的数字如何，网络犯罪足以称得上是一个重大问题，美国司法部和联邦调查局两个部门都有整套班子盯着这类犯罪活动。

把注意力集中在网络犯罪上的执法人员，大多在工作中使用各种数学工具。他们在这一领域，天才般地使用一些深奥的数学知识，已经取得了重大的进展，这些成果为互联网通讯的安全提供非常可靠的保障。但是道高一尺，魔高一丈，犯罪分子也在利用种种手段与执法人员较量。

从古到今的加密方法

当你使用自动取款机从银行账户上取钱，或向网络商家发送你的信用卡卡号和密码时，你当然会认为，只有认定的接受人才能获得你所输出的详情，不允许未授权的第三方“窃取”你发送的这些电子信息。然而，互联网是一个开放系统，这意味着组成网络的千百万台计算机之间的连接是公开的。互联网信息交流通道的安全保障只能借助于加密——即“改变”此信息，使得未经授权的第三方即使窃取到了所发射的信号，也搞不清它的含义。

加密的概念并不是什么新鲜事。使用秘密代码来保护秘密信息内容的想法，至少可以追溯到古罗马时代。当时罗马统帅尤利乌斯·凯撒就使用密码以确保高卢战争期间他送给将军们的命令的安全。现在把这种密码叫做凯撒码，在凯撒码中，原始信息中一个词中的每一字母都按某种固定规则由另一字母代替，例如，让字母表中的每一个字母由它后面的第三个字母代替，即A用D来代替，G用J来代替，Y用B来代替。这样一来，“mathematics”这个词就变成了“pdwkhpdwlfv”。

古罗马统帅尤利乌斯·凯撒

一个信息经过凯撒码加密后被传递出去，如果不知道所用的规则，表面上看它杂乱无章，完全无法辨认。但实际并非如此，因为英语只有26个字母，所以只有25套这样的“移位”密码，对你所用密码有怀疑的敌人只需依次一个个地来试，就能找到破解密码的“钥匙”。

另一种更好一些的方法是使用不像字母替代那样明显的其他规则。不幸的是，任何此类替代密码，即简单地用一个字母替代另一个，对于简单的模式分析来说都是不堪一击的。例如，出现在英语（或任何其他语言）中的字母都有非常确定的出现频率，通过计算你的编码文本每一个字母的出现率，敌人就可以简单地推导出你的替代规则。现在，计算机的使用，可以大大加速破解

过程。

除了简单的替代法外，当然你还能进行其他尝试。但是不管你如何选择，类似的危险还是会出现。只要你的编码文本包含任何一类可识别模式，一个老练的统计分析人员就能不太困难地破解此密码。

所以，第二次世界大战结束以来，所有的密码体系都依赖于数学，都使用计算机，而且不得不这样做。因为完全可以假设，敌人也有强有力的计算机用来分析你的加密信息，你的系统必须足够复杂，才能阻止计算机的破解分析。于是人们花了大量的时间和努力，设计和建立安全加密系统。

现代加密系统都包含两个组元：加密步骤和“密钥”。加密步骤一般是一个计算机程序或可能是一台专门设计的计算机。为了加密信息，这个系统不仅需要处理信息，还需要选定的密钥，它通常是个秘密的数字。加密程序以一种与所选密钥有关的方式来对信息编码，只有知道了密钥才能将加密文本解密。因为安全依赖于密钥，只要敌方得不到密钥，同样的加密程序可以被多人在一个较长的时期内使用而不致泄密。

有一个明显的类似密匙的例子，那就是保险箱或锁具的制造商，他们靠设计一种锁具销售给数以百计的用户来维持生意，这些用户凭借他们钥匙（实物钥匙、数字组合或两者的组合）的唯一性而确保安全。就像敌人尽管知道你的锁具是如何设计的，但没有实物钥匙或不知道该数字组合，还是不能打开你的保险箱那样;敌人知道你正在使用的加密体系的情况下，如果得不到密钥，他仍然不能破解你编码的信息。

在某些以密钥为基础的加密系统中，信息发送者和接受者事先约定好用某种密钥，然后用它来传送彼此的信息。只要保持了这个“钥匙”的秘密，这个体系（如果它是很好地设计的）则是安全的。1976年美国制订的数据加密标准（DES）曾使用多年，DES的密钥是一个56位的二进位数（换句话说，是56个0或者1组成的一串数字）。为什么要用这么长的密钥？因为DES设计的所有细节都曾被公布出来，这意味着敌人只要一个接一个地简单试用每一个可能的密钥，就可以破解你的编码信息。但是DES共有256个可能的密钥需要试用，这是个天文数字，所以在最初使用此系统的时，是几乎不可能被破解的。当然它现在已经老了，已经经不起新型的、比最初开发它时所用的快得多的计算机对它的

攻击。

同时，诸如DES这样的加密系统有一个明显的弊端，即传输信息前，发送方和接受方必须商定他们将要使用的密钥。很明显，在任何通信通道上发送密钥是不安全的，所以他们必须见面以转交密钥，或者找一个可靠的传递人转交密钥。这种加密系统，对于你与银行打交道是很合适的，因为你可以很方便地到银行的地区分支机构去建立一个供你个人使用的密钥。但是，这种方法特别不适用于网络商务，因为我们无法安全地把密钥交给世界某个地方的一个我们从未见过面的人。

公开密钥的加密算法

1976年，美国斯坦福大学两名青年研究人员怀特菲尔德·迪菲和马丁·赫尔曼发表了一篇里程碑式的论文，题目为“密码学的新方向”。在这篇论文中，他们提出了一种新类型的加密算法。在他们设计的密钥系统中，加密需要不是一个而是两个密钥——一个供加密用，另一个供解密用。这就像一具锁，需要用一把钥匙上锁，用另一把钥匙开锁。他们的建议可以用下面的假设例子通俗地解释。

一个人，让我们称她为艾丽斯，希望使用这个加密系统来传递保密信息，而购买了由某个通讯网络所有成员使用的标准程序（或特殊计算机）。然后，艾丽斯制作了两个密钥。其中一个是解密密钥，她把它秘密收藏好。另一个密钥由她在此网络用户的指南上公布，供此网络上的任何人要发送编码信息给她时使用。

如果网络中的另一用户叫鲍勃，希望送一条加密信息给艾丽斯，他查到艾丽斯的公开编码密钥，用此密钥将信息加密，然后将此信息传送给艾丽斯。要将信息解密，就需要收件人艾丽斯事先秘密收藏的解码密钥。而且这样的系统有一个特征：即当鲍勃用公开的密钥对信息加密后，连他自己也不能将它解密。所以如果他想以后查看它，最好的办法是保存原始信息，即未经加密的版本。

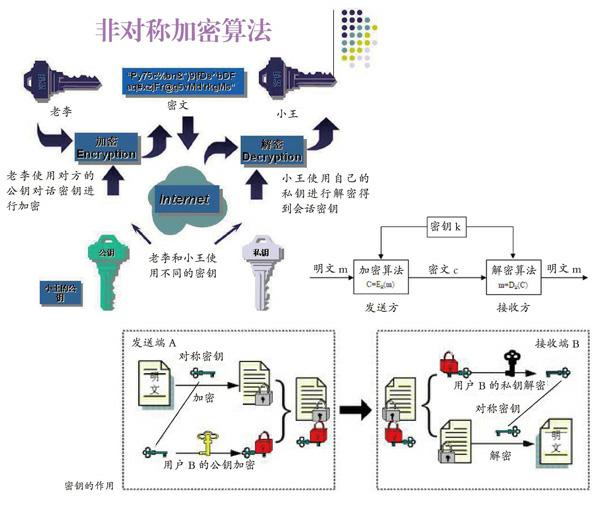
RSA系统加密法

然而，迪菲和赫尔曼虽然提出了这个了不起的方案，却没有能提出如何构造这样一个系统的具体方法。不久之后，美国麻省理工学院的三个研究人员罗纳尔·里夫斯特、阿里·沙米尔和伦纳德·阿德尔曼发现了如何去做这项加密工作的方法。这时就要用到“数学”这门高大上的学问了。

这种加密方法的基础是关于素数的数学知识。其实我们在小学数学中就学过，素数，又称为质数，即除了1和它本身以外不能再被其他的除数整除的数，比如2、3、5、7，可以参见下方图中的素数表。不少数学家已经证明，素数的个数是无穷多的。围绕素数数目的计算和素数分布的规律等问题，数学家们进行了大量研究，其中也有一些天才的猜想有待解决，包括我国数学家陈景润部分解决的哥德巴赫猜想以及上面提到的黎曼猜想等。

再回到如何应用素数的知识和规律来加密的问题。我们知道，编写寻找一个大素数（例如长达150位的素数）的计算机程序是相对容易的，将这样两个大素数相乘得到一个300位（或更多）的数（合数）也很容易。但是，反过来，要将这么大的合数分解为它的素因子，那就不是一件容易的事，事实上，几乎根本是不可能的。更正确地讲，用最快的计算机来寻找这样的素因子要化几十年，甚至几个世纪。基于这样概念的公开密钥系统叫做RSA系统，这是上面那三位发明人姓的首字母缩写。这个方法的成功导致成立了一个专门从事数据安全工作的商业公司—美国RSA数据安全公司。

具体来说，RSA方法中使用的解码密钥主要是由用户挑选的两个大素数组成。这里应当由计算机挑选，不要从任何公开的素数表中挑出，因为那是潜在的敌人很容易发现的。公开的编码密钥是这两个素数的乘积。因为不存在有已知的分解大数快速分解方法，要从公开的编码密钥揭露出解码密钥，即这两个素因子，事实上是不可能的。

我们需要指出，编码实际上并不是将两个素数相乘得到，解码也不是由分解因子来进行，而是指密钥是如何产生的，具体方法因为很复杂，就不详细介绍了。概括地说，要加密的信息首先被转换成数字形式，用相当简单地用数字进行算术运算，就构成了编码和解码

过程。

很清楚，RSA系统的安全性（这是许多国际数据网络使用它的原因）是建筑在数学家不可能发现大数因子化的有效方法的基础上的。

正如你能期待的那样，赌注是如此之高，RSA系统的广泛使用大大地刺激了对寻找素数和将大数因子化的方法的研究。所以上述电视剧中提到伊桑解决了黎曼难题，实际上就是将大数因子化的一种方法。

顺便讲一句，原则上讲RSA系统（以及任何其他系统）加的密，无一例外都是可以破解的，只不过是时间长一些罢了，要花上几十年、甚至几个世纪。惟一从本质上讲无法解密的加密系统，只有一个，即目前还处于开发阶段的“量子密钥”。量子体系有一个奇特的性质：一个状态下，只要对它进行“测量”，它就会变掉。要破解量子密钥，就要对它“测量”，但一经“测量”它就变掉了，所以量子密钥是永远无法破解的。量子密钥是量子信息理论中的一个部分。我国在量子信息的研究方面，处于国际领先地位。

（本文材料主要取自《数学缉凶》一书，上海科技教育出版社2011年第1版）