复合函数单调性的求解策略

安徽省太和中学　岳峻

复合函数单调性的求解策略

安徽省太和中学岳峻

我们知道，在复合函数y=f［g（x）］中，若内层函数u=g（x）在区间（a，b）上具有单调性，当x∈（a，b）时，u∈（m，n），且外层函数y=f（u）在区间（m，n）上也具有单调性，则复合函数y= f［g（x）］在区间（a，b）上一定是单调函数。单调性的判断规律可总结为：对于内层函数和外层函数，同增同减复合增，增减相异复合减，简而言之：同为增，异为减。

函数的单调性是高考的重点和热点内容之一，其中复合函数的单调性是高中数学的一个难点。如何求解复合函数的单调性呢？

一、外层函数与内层函数的单调性均为一种

例1函数f（x）=loga（4-ax）（a＞0，a≠1）在［0，1］上单调递减，则a的取值范围是（）。

A.（1，4］B.（1，4）

C.（4，+∞） D.［4，+∞）

解析（1）函数的定义域须满足：4-ax＞0。

（2）还原复合函数的复合过程：此函数由函数y=logau，u（x）=4-ax复合而成。

（3）内层函数的单调区间：因a＞0，函数u（x）=4-ax在［0，1］上单调递减，且u∈［4-a，4］。

（4）外层函数的单调区间：当0＜a＜1时，函数y=logau在u∈［4-a，4］上单调递减；当a＞1时，函数y=logau在u∈［4-a，4］上单调递增。

（5）因为函数f（x）=loga（4-ax）在［0，1］上单调递减，而函数u（x）=4-ax在［0，1］上单调递减，根据复合函数的单调性规律，可知：a＞1，且4-a＞0。

故答案为B。

评注研究函数的单调区间必须遵循“定义域优先”的原则，不能忽视4-ax＞0在［0，1］上恒成立这一条件。

变式1函数f（x）=loga（4-ax）（a＞0，a≠1）在［6，8］上单调递增，则a的取值范围是（）。

二、外层函数的单调性只有一种，内层函数有多种单调性

例2求函数的单调区间。

解析（1）函数的定义域：（-∞，1）∪（3，+∞）。

（3）内层函数的单调区间：函数u（x）=x2-4x+3在（-∞，2］上单调递减，在［2，+∞）上单调递增。

评注探求此类复合函数单调性的五步骤：（1）确定定义域，函数的单调区间必须是函数定义域的子区间。（2）还原复合函数的复合过程。（3）确定内层函数的单调区间。（4）确定外层函数的单调区间。（5）根据复合函数的单调性规律，确定复合函数的单调区间。对于函数的单调区间，包不包括端点都可以，但是，若单调区间端点在定义域之中，最好用闭区间。

解析（1）函数的定义域：（-∞，1）∪（1，5）∪（5，+∞）。

（2）还原复合函数的复合过程：此函数由函数y=logsin3u，u（x）=|x2-6x+5|复合而成。

（3）内层函数的单调区间：函数u（x）=|x2-6x+5|在（-∞，1）上单调递减，在（1，3）上单调递增，在［3，5）上单调递减，在（5，+∞）上单调递增。

（4）外层函数的单调区间：函数y=logsin3u在（0，+∞）上单调递减。

（5）根据复合函数的单调性规律，函数y=logsin3|x2-6x+5|在（-∞，1）上单调递增，在（1，3）上单调递减，在［3，5）上单调递增，在（5，+∞）上单调递减。

三、外层函数的单调性有多种，内层函数只有一种单调性

解析（1）函数的定义域：（0，+∞）。

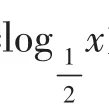
（3）内层函数的单调区间：函数u（x）=在（0，+∞）上单调递减。

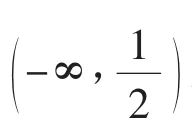
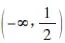
变式3函数f（x）=9x-2×3x+1+2的单调递减区间是____，单调递减区间是____。

四、外层函数与内层函数的单调性都有多种

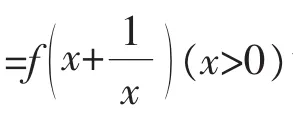
解析（1）函数的定义域：（0，+∞）。

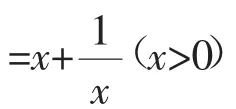
（4）外层函数的单调区间：y=f（u）=u2-8u+2在（-∞，4）上单调递减，在（4，+∞）单调递增。

变式训练答案：

变式3（-∞，1）（1，+∞）提示：函数f（x）=（3x）2-6×（3x）+2，外层函数y=u2-6u+2，内层函数u=3x。因为内层函数u=3x在R上单调递增，外层函数y=u2-6u+2在u∈（-∞，3）［⇔x∈（-∞，1）］上单调递减，在u∈［3，+∞）［⇔x∈［3，+∞）］单调递增，所以f（x）=9x-2×3x++2在（-∞，1）上单调递减，在［1，+∞）上单调递增。