创意平板折叠桌的优化设计

王二耀，陈培军，王欣洁，卫慧慧

（太原科技大学应用科学学院，太原　030024）

创意平板折叠桌的优化设计

王二耀，陈培军，王欣洁，卫慧慧

（太原科技大学应用科学学院，太原030024）

创意平板折叠桌方便、简单并且极大地节约了空间，越来越受到消费者喜爱，因此对折叠桌的研究具有现实意义。文章利用相对位置不变的性质描述了钢筋质点运动轨迹，将三维转二维平面分析得到开槽长度，在此基础上求出平板折叠桌的桌腿在伸展前后旋转的角度。其次对桌腿和钢筋质点进行受力分析，最终以桌腿开槽长度最小，木板取材最少，折叠桌稳固性最好为目标函数约束优化设计并用Matlab编程求解。

质点；相对位置；稳定性；优化；Matlab

0　引 言

如今，伸展与折叠已经成为家具设计行业一个最佳创意理念。折叠桌因其空间占用面积小、并且便于操作而深受消费者的热捧与喜爱。因此对于既能满足基本生活需求又能节约空间的家居产品的探究就具有着现实性的重大意义。本文主要针对2014年全国大学生数学建模B题中平板折叠桌进行了最优化设计的研究处理分析。折叠桌的桌腿由若干长木条组成，对称分为2组，各用钢筋固定，并且沿桌腿有开槽以保证桌腿滑动的自由度。通过对开槽长度以及桌角边缘线的动态变化进行研究，在此基础上考虑折叠桌稳定性来约束优化。本研究旨在为折叠桌的优化设计提供更为周全的优化思路，在简单的考虑取材少的优化基础上，要同时保证折叠桌的稳定性和实用性。

1　模型准备

1.1符号说明

在此，给出研究中需要用到的符号说明，具体如表1所示。

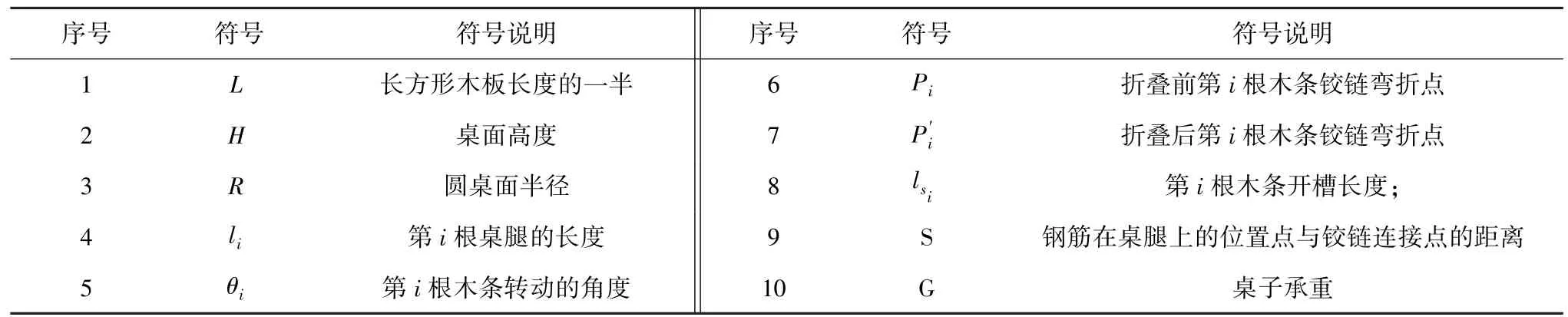
表1　符号说明Tab.1 Symbol description

1）假设钢筋为理想的不可发生形变的刚体，同时忽略钢筋的直径大小及重力；

2）假设所有木条紧密排列，没有间隙并且是光滑的；

3）折叠桌高度对称且只考虑等分的木条数为偶数的情形；

4）假设折叠桌未变形前钢筋位于凹槽的一端，展开后位于凹槽的另一端以保证桌子成型后的最佳稳固性。

2　模型建立

2.1研究思路

对于折叠桌的最优化设计，首先需要确定圆形折叠桌弯折处的木条铰链的位置情况。如图1所示，为了保证折叠后桌面呈现圆形，必须使铰链弯折点分布在桌面圆周上，这样就需要确定最外侧的木条铰链弯折点。找到那些相对位置不变的点的关系以及关键节点之间的相对运动轨迹，从而描述折叠桌的动态变化过程。该动态变化过程可如图2所示。通过钢筋质点相对桌面弯折点的运动轨迹、每根木条与钢筋相交位置的运动轨迹、每根木条在折叠过程中转动的角度等方面的分析，建立折叠桌的动态变化模型，进而求出开槽长度，以及做出对桌脚边缘线的数学描述。关键在于对折叠桌的稳定性进行受力分析，并以此为基础求出受力表达式。折叠获得最优化在于木条长度最短，开槽长度最小，承受力最大，因此将这3部分组合即可得到最优化设计的目标方程。

图1　折叠桌成品展示Fig.1 Folding table display

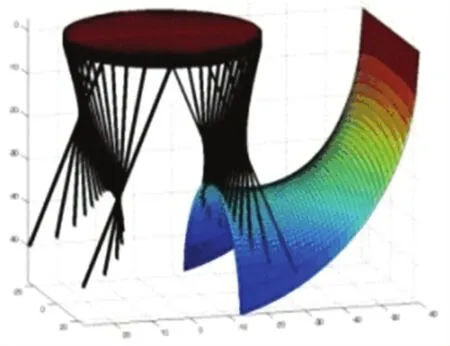
图2　折叠桌脚边缘线动态变化Fig.2 Dynamic changes of folding table base edge lines

2.2折叠桌的开槽长度

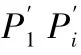
在模型运用中，选取调节系数z=2，本文视土地综合承载力和区域经济发展同等重要，给待定权重赋值为ξ=ζ=0.5。因此，根据式(2)～式(3)分别测算北京、天津、河北、京津冀城市群土地综合承载力与区域经济发展的协调度、整体效应、耦合协调发展度(见表6)。

转动过程的与钢筋质点G的相对位置示意如图3所示。

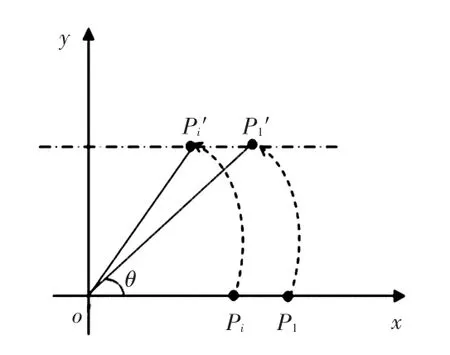
图3　相对位置示意图Fig.3 A schematic view of the relative position

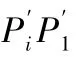
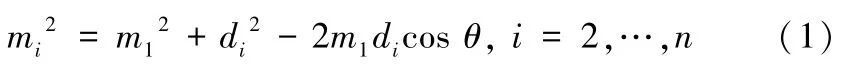
由此可得第i根木条相对于钢筋的运动轨迹即为开槽的长度，记为lSi， 则

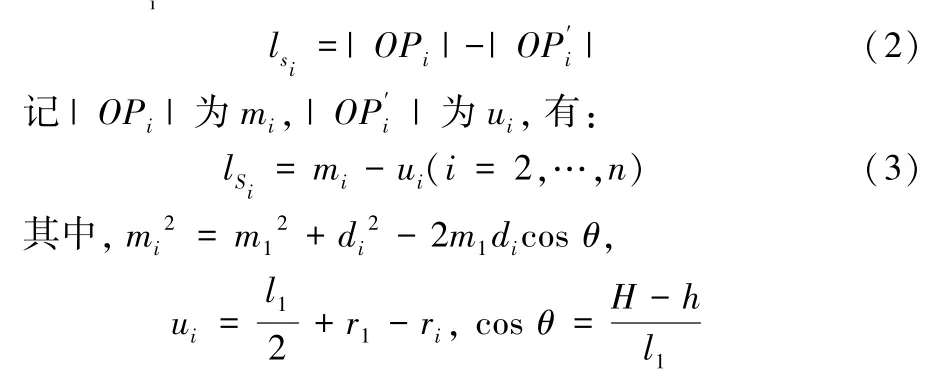
将第i根木条转动的角度记为θi，由图3可得：

而在△OP1Pi中利用余弦定理

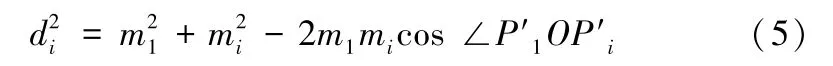
即可求出∠PiOP1，故可得：

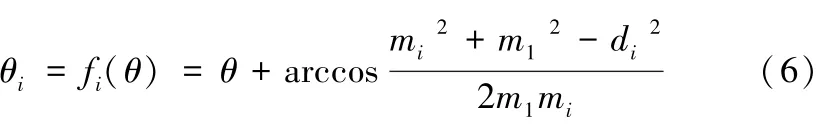
2.3折叠桌取材长度

折叠桌的构成材料主要是长木板，长木板在折叠桌成型后取材最小表示为折叠桌的桌腿长度最短。

在折叠桌的最优化设计分析中，因为折叠桌的高度对称，在此仅以长木条的一半以及平板的四分之一去研究问题，即：

其中，ri表示构成桌面的第i根木条的一半；li表示第i根桌腿的长度。

2.4折叠桌稳定性分析

结构的稳定性是指结构在载荷作用下维持其平衡形式的能力。要使得折叠桌具有良好稳定性，就必须分析折叠桌桌腿以及钢筋质点的受力关系。折叠桌折叠后，就可以直观看到在所有的桌腿中处于最外侧的4根桌腿承受着来自桌子和桌子上所放物品的重力之和G，而除此之外的桌腿承担着沿桌腿方向的拉力并且通过力的传递最后还是由最外侧的桌腿来承担所有的重力。受力分析如图4所示。

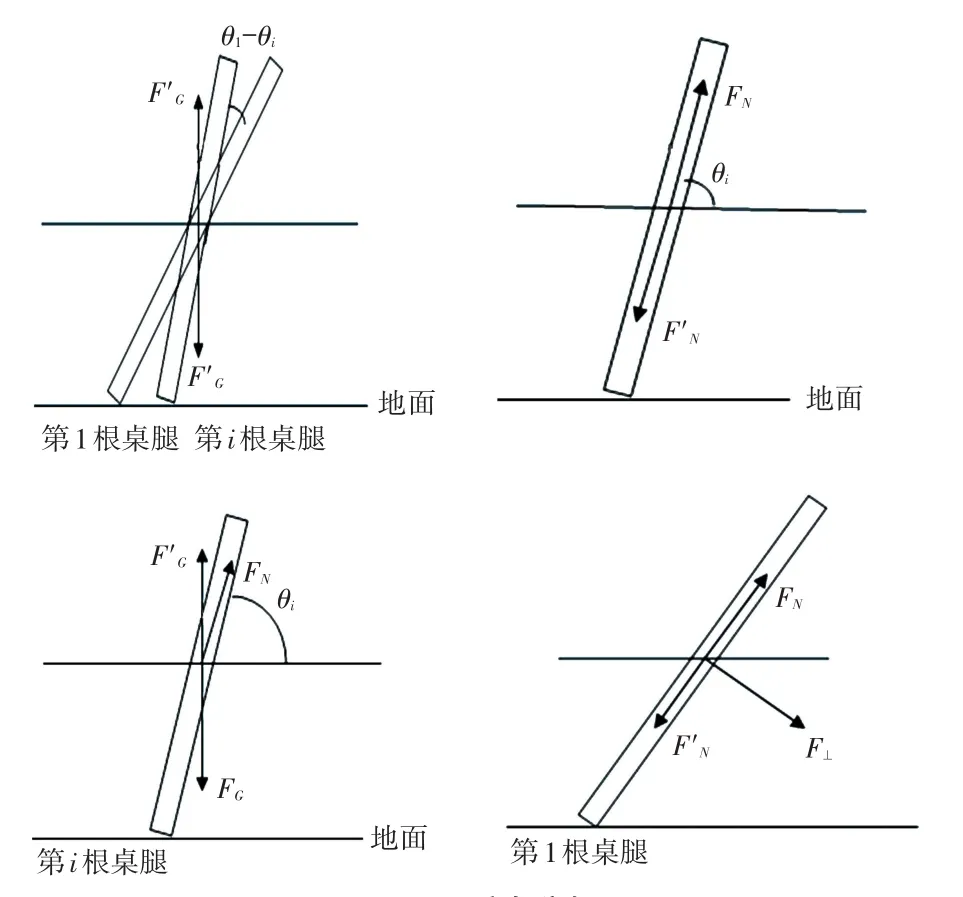
图4　受力分析Fig.4 Mechanical analysis

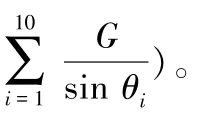
2.5建立目标函数

折叠桌的最优化设计要使得长方形材料的取材长度最小、木条的开槽长度最小和桌子的稳定性最好，即桌腿能够承受的压力最大，在此简化为第1根桌腿承受的来自桌子及重物的压力。综合以上约束条件可以得到：

目标函数：

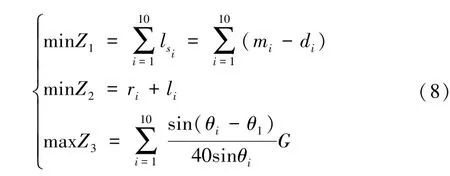
约束条件：

3　模型求解

编写Matlab程序，设置值L=70，h=3，W=2.5，R= 40，r1=5，求出对于桌高70 cm，规格直径80 cm的情形，确定最优设计加工参数平板长度至少为162 cm，即尺寸为162 cm、80 cm、3 cm的平板通过切割可以折叠成所需尺寸的圆桌。具体设计参数如下：以平板左下角长度方向为x轴，宽度方向为y轴建立坐标系，则桌腿上4个钢筋固定点的坐标为（38，0），（38，80），（124，0），（124，80），每根桌脚长度、木条的开槽长度、桌腿旋转角度如表2～表4所示。由于对称性，这里只显示一半的加工参数，其他值由此推算。

表2　桌腿的长度（单位：厘米）Tab.2 Length of legs（Units：cm）

表3　木条的开槽长度（单位：厘米）Tab.3 Slot length of wood（Units：cm）

4　结束语

本文在折叠桌最优化设计的目标函数中加入开槽长度以及稳定性的分析，使得折叠桌的设计更趋于合理化，这一设计理论与实际相结合，通过MATLAB将该方案部署实施编程，后期只需要输入已知参数智能程序就可以得到相应设计参数。在家具设计行业将这一方案运用实际，那么所设计的折叠桌就不仅仅满足客户任意设定的折叠桌高度和桌面形状，而且仍可以具有优质的承重能力，也更加符合桌子该有的实用性。

［1］韩佳成，EMBRICQS R V.平板折叠边桌［J］.设计，2012（8）：24.

［2］苏金明，阮沈勇.MATLAB实用教程［M］.北京：电子工业出版社，2005.

［3］刘金春.结构力学［M］.武汉：华中科技大学出版社，2008.

［4］王沫然.MATLAB与科学计算［M］.北京：电子工业出版社，2003.

［5］侍冰雪，朱家明，朱韶东，等.创意平板折叠桌优化设计方案［J］.浙江科技学院学报，2014，26（6）：429-435.

The optimization design of flat pembroke table of innovative idea

WANG Eryao，CHEN Peijun，WANG Xinjie，WEI Huihui
（College of Applied Science，Taiyuan University Of Science and Technology，Taiyuan 030024，China）

Flat pembroke table of innovative idea is simple and has saved space immensely，and it becomes more and more popular，therefore it has practical significance to the pembroke table research.The article makes use of the invariant character of relative location to describe the trajectory of reinforced bar particle.Revolution of 3-D to two-dimensional flat surface gets the slotting length，asking table angle border to count space coordinate out and then getting the table angle border line on the basis of equation changes.And table leg and reinforced bar particle are analysed by the force.Therefore，the paper proposes target function constraint optimization design in which centering on result stability，the length is minimal，and materials are drawn with slotting to be short most.Furthermore，the paper gives out the solution with Matlab.

particle；relative location；stability；maiorization；Matlab

TP312

A

2095-2163（2016）03-0068-04

2016-04-23

国家级UIT项目（G2015269）。

王二耀（1994-），女，本科生，主要研究方向：数学与应用数学；陈培军（1978-），男，博士，副教授，主要研究方向：图像处理、组合优化、智能计算；王欣洁（1981-），女，硕士，讲师，主要研究方向：数值计算、最优化方法；卫慧慧（1994-），女，本科生，主要研究方向：信息与计算。