基于曲面拟合的三维面形拼接算法

吴家亨，蔡志岗

（中山大学物理学院，广州广东 510275）

基于曲面拟合的三维面形拼接算法

吴家亨，蔡志岗

（中山大学物理学院，广州广东 510275）

针对大尺寸物体的三维面形测量，提出了一种曲线函数形式的图像镶嵌算法.将测量到的两个或两个以上的面形通过重叠区域的数据融合实现面形测量，较好地实现了整个拼接区域的平滑过渡.仿真实验结果表明，该方法运算量小，速度快，可操作性强.

三维测量；曲面拟合；信息光学；数据融合

0　引言

光栅投影三维面形测量具有非接触性、测量精度高、速度快、易于自动化等优点，在制造业、产品检测、文物保护、生物医学等领域有着广泛的应用［1-6］.对大尺寸物体面形的测量，其高精度方面难以单纯依靠CCD相机性能的提高来实现，一方面是系统成本太高，另一方面是可以通过拼接实现同样的精度.子区域进行拼接时，相邻两个子区域会有相互重叠的部分，通过拼接区域内部线性加权平均实现拼接是最常用的方法.通常是将拼接边界到中心的距离作为权重，实现拼接区域内高度数据的拼接，但是传统方法在拼接过程中会出现间断点，影响数据拼接的平滑性［7］.本文提出一种基于曲线拟合的拼接算法，引入一种曲线函数形式的融合算法实现三维数据的拼接.

1　测量原理

由投影一正弦光栅产生的光场到三维漫反射物体表面时，由成像系统得到的变形条纹图可表示为

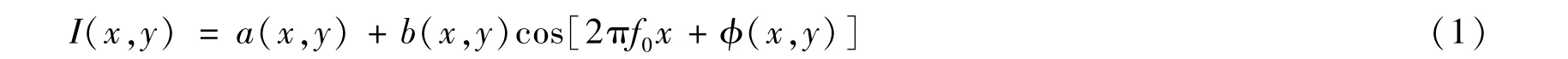
式中，a（x，y）是背景强度，b（x，y）表示条纹对比度率，f0是光栅像的基频，φ（x，y）是物体高度分布h（x，y）引起的位相调制.

对式（1）作傅里叶变换，对其滤波取出基频，再对其进行逆傅里叶变换得到

同理，对投影到参考面上的条纹作傅里叶变换、滤波、傅里叶逆变换等操作可得

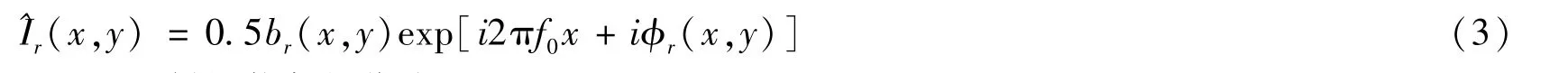
所以由高度h（x，y）调制的截断相位为

式中，Im｛｝表示取复数的虚部，*表示共轭运算.

由式（4）得到的相位受反三角函数主值范围的限制，因此展开的相位分布必须连续，才可以恢复出变形条纹的相位分布.最后依据相位与高度的映射关系恢复出物体的三维面形h（x，y）.

2　数据融合

采集到图像的重叠区域可以通过调制度信息的相关性来确定.如果简单的将测量数据拼接，由于测量误差的存在，效果不好，必须进行有效的数据融合.传统方法是迭代和最小二乘方法［1，2，8］进行数据融合，其涉及到的计算量很大，若利用线性插值或曲面拟合的方式，在一定程度上可以降低计算量.假设两次测量重叠区域的面形分别为h1（x，y）、h2（x，y），进行有效的拼接后三维面形重叠区域的面形为h（x，y），则有

式中k作为渐变系数，由0渐变到1.最简单的方法就是令k=xi/d，d是重叠区域的宽度.利用这种拼接边界突变的算法，在很大程度上影响了数据的平滑，因此拼接的图像中有明显的拼接痕迹.

下面通过k值分析两三维面形的重叠区域的拼接情况.在拼接区域内任意一行，重叠区域边界两点不妨设为x1、x2，通过式（5），拼接后的图像如图1所示.

从图1可以看出，拼接区域的x1、x2处出现了间断点，在拼接图像中会导致明显的拼接痕迹.

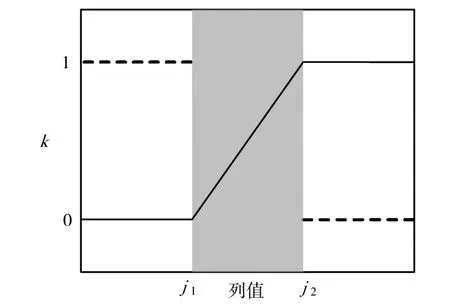
图1　传统方法k值曲线图

图2　改进方法k值曲线图

为实现在拼接区域内无间断点，同时实现三维数据的融合，在重叠区域内任意一行用曲线达到平滑的目的，则其充要条件为在［x1，x2］内连续且可导.为此，对k进行必要的改进，引入曲线函数，令

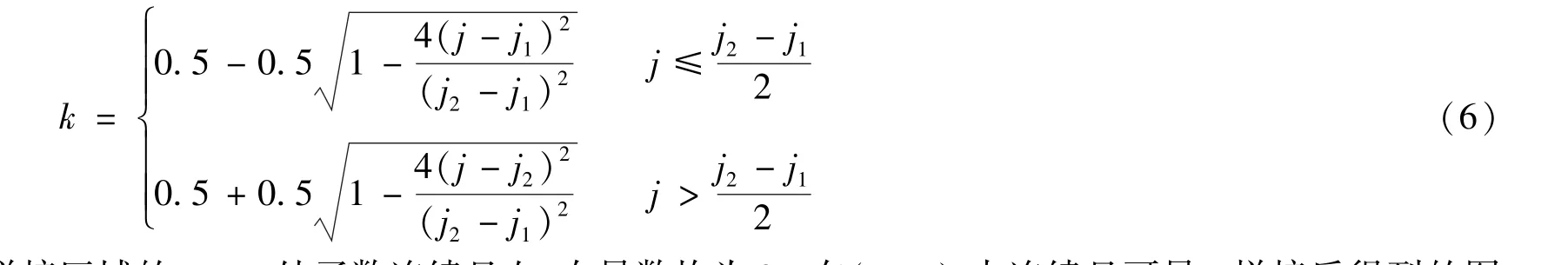
变化曲线拼接区域的x1、x2处函数连续且左、右导数均为0，在（j1，j2）内连续且可导，拼接后得到的图像在拼接区域内无间断点，使得数据高效融合.对渐变系数k进行改进后得到的k值曲线如图2所示.

3　仿真实验

改进算法后对其进行了计算机仿真，模拟物体为一个半椭圆球体，如图3所示.投影到参考面的

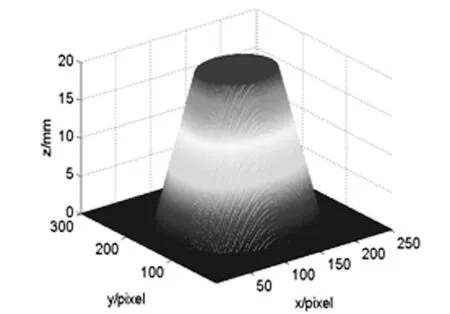
图3　模拟物体

图4　恢复的物体面形1

变形光栅像大小为301×251 pixels，T=32 poxels，图4表示投影系统光轴与成像系统光轴夹角为200时，测量获得的面形分布图.图5表示从另一个方向投影、成像获得物体的三维面形.采用本文提出的算法，对从不同角度获得的三维面形图4和图5进行拼接，拼接的结果如图6所示.由图6可以看出，利用本文提出的算法，较好地恢复出物体的面形分布.

图5　恢复的物体面形2

图6　面形1和面形2拼接结果

4　结论

针对面形恢复时所得数据不够精确可能会导致误差较大的问题，提出利用曲面函数进行数据融合实现拼接的方法.有效的解决了以往传统线性拼接中由于边界断点导致拼接精度不够高的问题，相对提高了测量精度.仿真结果也显示，利用改进的方法使得数据融合的精度相对较高，无断点，满足正常的面形测量需求.

［1］ Guo H W，Chen M Y.Multiview connection technique for 360-deg three-dimensional measurement［J］.Optical Engineering，2003，42（4）：900-905.

［2］ 张蓉竹，杨春林，石琦凯，等.子孔径拼接干涉检测及其精度分析［J］.光学学报，2003，23（10）：1241-1244.

［3］ 边心田，陈文静，孙娟，等.自动搜索匹配区域消除阴影影响的拼接算法［J］.光电工程，2007，34（10）：55-58.

［4］ 边心田，陈文静.FTP中采用双帧条纹消除阴影影响的高度拼接讨论［J］.激光杂志，2007，28（2）：44-45.

［5］ 陈文静，陈锋，苏显渝，等.CCD抽样过程对傅里叶变换轮廓术测量的影响［J］.光电子激光，2005，16（9）：1074-1079.

［6］ Guo H W，He H D，Yu Y J，et al.Least-squares calibration method for fringe projection profilometry［J］.Opt Eng，2005，44（3）：033603.

［7］ 罗文斐，李岩，王小铭.基于平滑渐进图像镶嵌的新算法研究［J］.计算机工程与应用，2004（36）：50-53.

［8］ 李勇，苏显渝，吴庆阳.双摄像机相位测量轮廓术系统标定与数据融合［J］.光学学报，2006，26（4）：551-556.

Height Mosaic Based on Surface Fitting Method

WU Jia-hen，CAI Zhi-gang
（School of Physics，Sun Yat-sen University，Guangzhou Guangdong 510275，China）

A new method is proposed based on curve function mosaic algorithm in the 3D shape measurement of large size object.Two or more object may be measured through the overlap region of the data fusion to achieve 3D shape measurement.This method is good to achieve the smooth transition of the entire region.The results show the operation amount of this method is small，speed is fast and maneuverability is strong.

3D measurement；surface fitting；information optics；data fusion

TP391.41

A

1671-6876（2016）03-0211-03

［责任编辑：蒋海龙］

2016-06-15

蔡志岗（1962-），男，福建厦门人，教授，博士，主要从事激光与光电测量技术研究.E-mail：lasers@netease.com