高速列车非定常气动力及其波动特性的雷诺数效应*

牛纪强　梁习锋　周丹　刘峰

(中南大学 交通运输工程学院∥轨道交通安全教育部重点实验室， 湖南 长沙 410075)



高速列车非定常气动力及其波动特性的雷诺数效应*

牛纪强梁习锋周丹刘峰

(中南大学 交通运输工程学院∥轨道交通安全教育部重点实验室， 湖南 长沙 410075)

基于Realizableκ-ε湍流模型的延迟分离涡模拟(DDES)方法，求解不同缩比尺度和来流速度下列车周围非定常流场.通过改变模型缩比尺度和来流速度来研究列车非定常气动特性的雷诺数效应和尺度效应.研究结果表明：随雷诺数增加，各节车气动阻力系数均方根基本呈现减小趋势，且波动明显；随雷诺数增大，列车各节车气动阻力系数和升力系数标准差均先减小后增大，且波动明显；气动力系数功率谱密度随雷诺数增大而变小；雷诺数对气动力系数主频有影响，但无明显规律；列车气动力的尺度效应显著，随雷诺数增大，列车气动力的尺度效应减弱，且列车升力的尺度效应相对显著；列车非定常气动阻力和升力振动的尺度效应随雷诺数增大而减弱，且列车非定常升力振动的尺度效应更加显著；尺度效应不改变列车气动力以低频为主的振动特性和列车气动力功率谱密度的分布规律，对气动力振动主频及其功率谱密度有显著影响.

高速列车；非定常气动力；雷诺数效应；尺度效应；功率谱密度

随着列车速度的不断提高，列车气动特性日益凸显[1].列车周围的强湍流会引起列车的振动，长期的气动振动会引起列车结构、材料等产生疲劳损坏，缩短车辆使用寿命，影响列车安全运行，甚至可能威胁到旅客的生命财产安全.

国内外学者采用数值模拟、实车试验等方法对列车振动特性进行了大量研究[2- 6].任尊松等[7]通过分析实车试验列车振动特性，得到了高速动车组振动传递及频率分布规律.宁迎智等[8]采用小波分析研究了轨道不平顺和车体振动响应.国内外研究单纯由气动效应引起的列车振动特性的文献也较多.刘加利等[9- 10]采用大涡模拟的方法对横风下列车的非定常气动载荷特性进行了研究，确定高速列车非定常气动载荷的主要峰值频率集中在0～5 Hz.杨志刚等[11]采用大涡模拟的方法研究了横风下高速列车的非定常气动力特性，发现在高速列车所受非定常空气动力的频域特性方面，其峰值频率集中在0.5～2.0 Hz.马静等[12]研究了横风下高速列车的非定常空气动力特性，发现非定常气动力的特征频率出现在11 Hz以下，并且主要峰值集中在0～3 Hz.郭迪龙等[13]采用分离涡方法研究了受电弓的非定常气动振动特性，受电弓脱体涡的强度、脱落频率对受电弓气动升力系数影响很大.郗艳红等[14]采用分离涡方法模拟研究了横风作用下转向架非定常气动力特性，发现各个转向架的空气动力的功率谱密度存在明显峰值.

风洞试验一般采用缩比模型，为满足壁面y+的要求，数值计算中也常常采用缩比模型.然而，缩比模型的雷诺数有时与全尺寸模型的雷诺数差1至2个数量级.文献[15]指出，雷诺数效应会导致缩比模型的气动力、压力等结果在外推到全尺寸模型时产生较大误差.国内外学者采用数值计算和风洞试验手段对列车这种长大近地面且受地面强剪切流影响的物体的气动性能雷诺数效应研究相对较多，对列车气动振动特性的雷诺数效应的研究则鲜有涉及[16- 18].

文中采用延迟分离涡模拟方法对不同来流风速和缩比尺度下列车周围的非定常流场进行模拟，并对列车非定常气动力振动特性进行对比分析.

1　数学模型

文中主要研究的是列车气动振动的雷诺数效应，首先要保证模拟的列车气动振动数据的精度.采用直接模拟(DNS)，对流场的模拟和湍流脉动的捕捉是最精细的，但是该方法对空间和时间分辨率要求过高，对于模拟高雷诺数、多尺度特征长度的长大、近地面运行的列车周围流场，目前的计算条件难以满足.按照湍流的涡旋学说，湍流的脉动与混合主要是由大尺度涡造成的，小尺度涡主要用于能量耗散[19].由此，可以将涡旋尺度分为含能区、惯性副区和耗散区.流体内部多尺度涡旋的随机运动造成流场中物理量的脉动，从而引起列车上气动力的振动.引起列车气动力振动的储能区和惯性副区内尺度的涡需要主要关注，而对于处于耗散区的涡可以近似模拟.

大涡模拟(LES)的主要思想是对各向异性大尺度涡采用直接数值模拟，而对滤去的各向同性小尺度涡采用亚格子模型进行求解.这种基于网格滤波的方法关键在于找到适宜的滤波尺度，这直接关系到模拟计算的准确性.根据湍流能谱分布，理论上适宜的滤波网格尺度应位于惯性副区内[20].基于湍流统计理论[21- 22]和湍流Kolmogorov理论[23]中“-5/3”惯性副区能谱分布公式可推导出LES中适宜滤波的网格尺度计算公式为

文中采用基于Realizableκ-ε的延迟分离涡模型.该模型确保在整个边界层内都使用时均的Reali-zableκ-ε模型，边界层以外区域使用LES模型.其中，时均的Realizableκ-ε耗散项被修改为

Yκ=ρκ1.5/ldes

(1)

式中:ldes=min(lrke,lDES)，lrke=κ1.5/ε，lDES=CDESΔ;CDES为DES湍流模型的常数项，取0.61.

将列车视为静止物体，采用在列车运行方向吹风的相对运动的方法来模拟列车明线运行[25- 26].来流风速60 m/s，马赫数小于0.3，即可忽略空气压缩性.本次数值计算中，将模型列车高度H(车顶距轨面高)视为列车特征长度，此时列车周围流场雷诺数一般大于105，即列车周围流场处于强湍流状态.由于Realizableκ-ε湍流模型在预测列车阻力方面具有优势[27- 28]，而且文献[29]中采用基于Realizableκ-ε湍流模型的DES方法模拟高速列车流场，获得的结果与风洞试验数据具有很好的吻合度.因此，本次模拟采用粘性、不可压缩N-S方程及Realizableκ-ε湍流模型求解定常状态的流场，采用基于Realizableκ-ε湍流模型的延时分离涡模拟DDES方法求解非定常流场，并获得列车非定常气动力及压力的时程曲线.

2　计算模型、区域及边界条件

2.1计算模型

本次计算采用头车(6.9H)+中间车(6.6H)+尾车(6.9H)3车编组的高速列车作为计算模型，总长20.8H，其中H为车高(轨道至车顶距离)，如图1所示.文中通过改变列车缩比尺度和来流速度来调整列车周围流场的雷诺数，其中还涉及到尺度效应，通过改变缩比尺度和流速，对比分析了同一雷诺数下的列车尺度效应影响.

图1　高速列车模型

列车外形复杂，转向架、受电弓等部件与车体的特征长度相差一个数量级以上，即列车是一个多尺度的物体,而文中研究的内容包含振动特性和雷诺数效应，为得到准确的模拟结果，在处理车体表面及空间网格上难度很大，容易造成模拟结果的失真.因此，在节约计算资源和保证精度的前提下，对列车模型表面做了必要且合理的简化，省略了车体表面的扶手、转向架和受电弓等部件.由于需要准确模拟车体附面层,捕捉涡结构的形成、发展以及脱落，车体壁面第一层网格初始厚度小于1 mm，并且保证附面层网格长细比小于10∶1，且对车体附近流场区域网格进行局部加密处理.为节约计算资源，考虑到远离列车区域对列车气动力和列车周围流场结构影响有限，故空间体网格设置相对较为稀疏，共计4×107左右.列车局部网格如图2所示.

2.2计算区域

为保证流场充分发展，避免边界对列车周围流场结构的影响，计算域X方向长度为70H，Y方向宽度为20H，Z方向高度为20H;为避免入口边界的影响，列车头部鼻尖点距入口边界18H;为避免出口边界条件对列车流场及尾涡变化的影响，尾涡区域长为31.2H.以上设置完全满足欧标中对数值模拟中计算域上游大于8倍特征长度、下游大于16倍特征长度的要求.列车计算区域如图3所示.

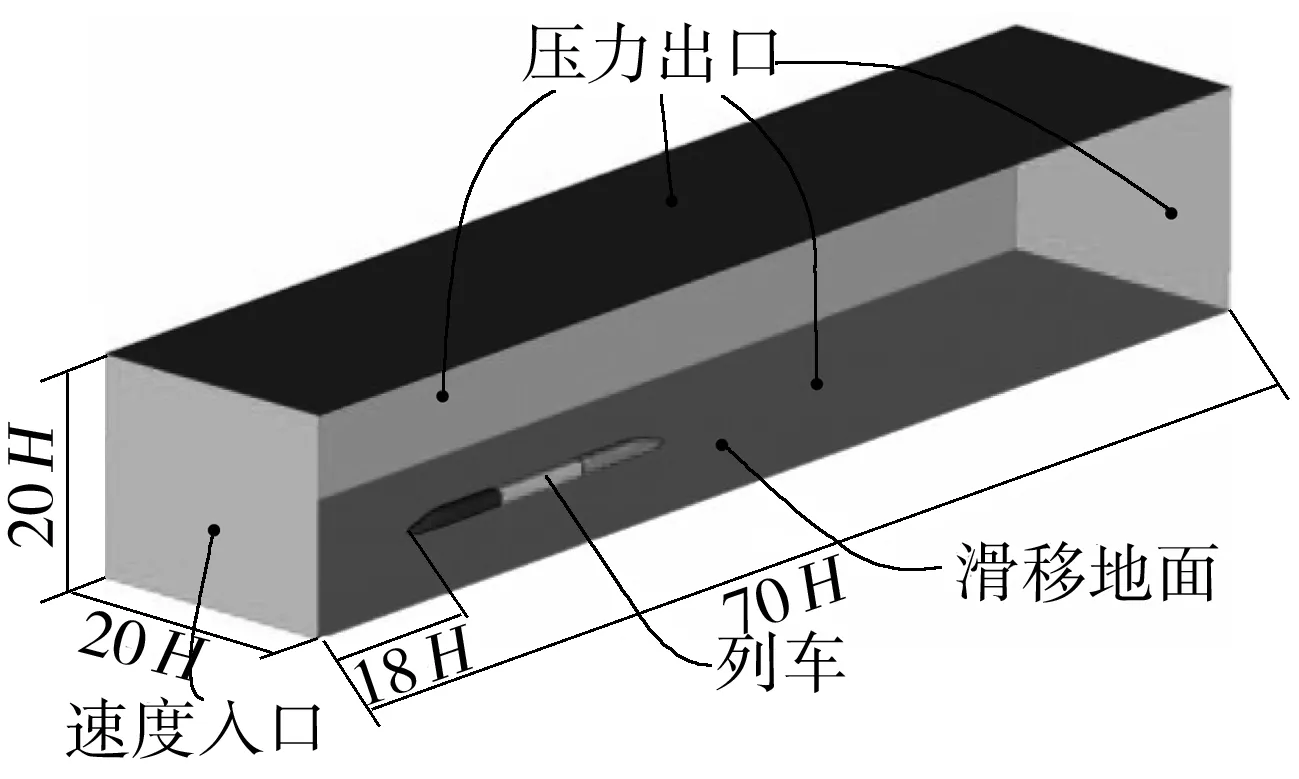
图3　计算区域示意图

2.3边界条件

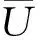
(2)

I=0.16Re-0.125

(3)

(4)

(5)

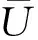
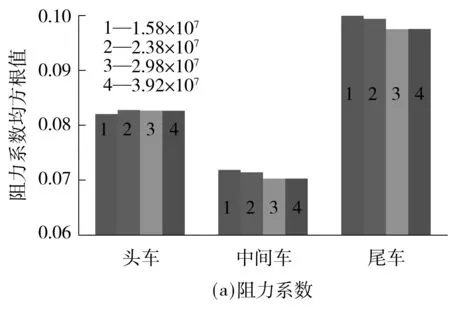
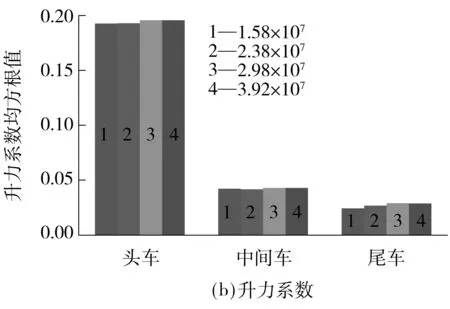
图4　不同网格数量下的车辆气动力系数均方根值

2.4网格无关性验证

从图4中可知:对于列车阻力系数而言，随着网格数量增加，头车呈增长趋势，均方根值增幅不超过0.9%；中间车和尾车均呈减小趋势，均方根值降幅均分别不超过0.9%、2.3%和4.0%；对于列车升力系数而言，随着网格数量的增加，头车、中间车和尾车均呈增长趋势，均方根值增幅分别不超过1.5%、2.8%和15.3%.网格数量分别为2.98×107和3.92×107时的列车气动力系数的均方根值间的差异均不超过0.5%.

从图5中可知，随着网格数量增加，列车阻力系数和升力系数的标准差均呈增长趋势，且当网格数量在3.0×107以上时，其气动力系数标准差随网格数量变化率减缓，网格数量分别为2.98×107和3.92×107时的列车气动力系数的均方根值间的差异均不超过5%.因此，文中网格规模在4.0×107以上时，满足本次模拟计算要求.

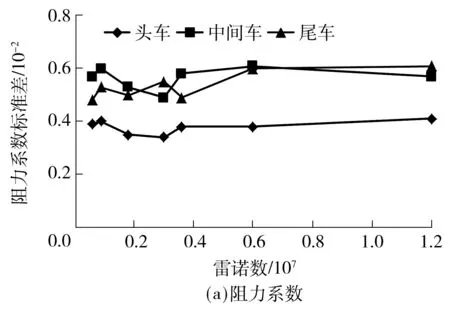
图5　不同网格数量下的车辆气动力系数标准差值

Fig.5SD of unsteady train’ aerodynamic coefficients for diffe-rent grid numbers

2.5气动力系数定义

为便于分析，对气动力进行无量纲化，定义各气动力系数如下：

(6)

(7)

式中，ρ=1.225 kg/m3，S为参考面积，此处为模型列车中部横截面，取S=11.2/(3.7/H)2m2.D为阻力，L为升力，CD为阻力系数，CL为升力系数.

3　计算结果及分析

采用Openfoam开源软件对流场进行网格划分，基于商业软件ANSYS 15中的Fluent模块进行流场求解.为保证计算过程稳定，满足结果准确的要求，定常计算中速度压力耦合采用SIMPLEC算法，对流项采用具有二阶迎风格式离散，扩散项采用具有二阶精度的中心差分格式离散；非定常计算中采用SIMPLE算法求解质量守恒方程，对流项采用二阶迎风格式离散，扩散项采用中心差分格式离散，采用二阶隐式进行时间推进.模拟计算在国家超算广州中心的天河2号超级计算机上进行，单个工况采用5×24个CPU，计算步长Δt=0.5×10-4s，每个步长取一次数据，非定常时程长5.0 s左右，单个工况计算时长800 h左右.

3.1气动力振动特性的雷诺数效应

图6为不同雷诺数下车辆气动阻力系数和升力系数的时程曲线.从图中可知：列车非定常气动力系数振动显著，具有强非定常性；不同雷诺数下，列车气动力系数存在明显差异.

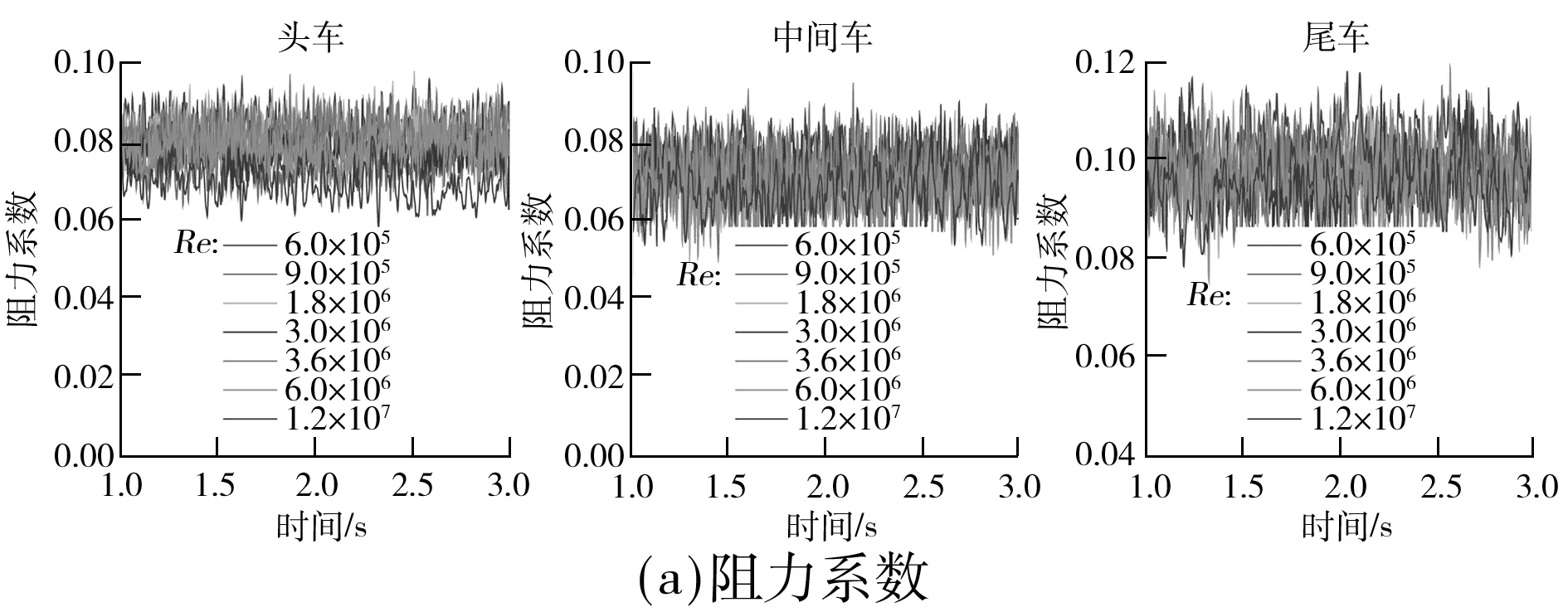
图6　列车非定常气动力系数时程曲线

Fig.6History curves of unsteady aerodynamic force coefficients of train

为便于比较不同雷诺数下列车气动力系数，采用非定常气动力系数的均方根值来对比分析列车非定常气动力的雷诺数效应.

图7为列车阻力系数和升力系数均方根值随雷诺数的变化曲线.从图中可知：随雷诺数增大，列车各节车气动阻力系数呈减小趋势，且波动明显；气动升力系数存在明显波动，随雷诺数增大其基本呈现减小趋势.

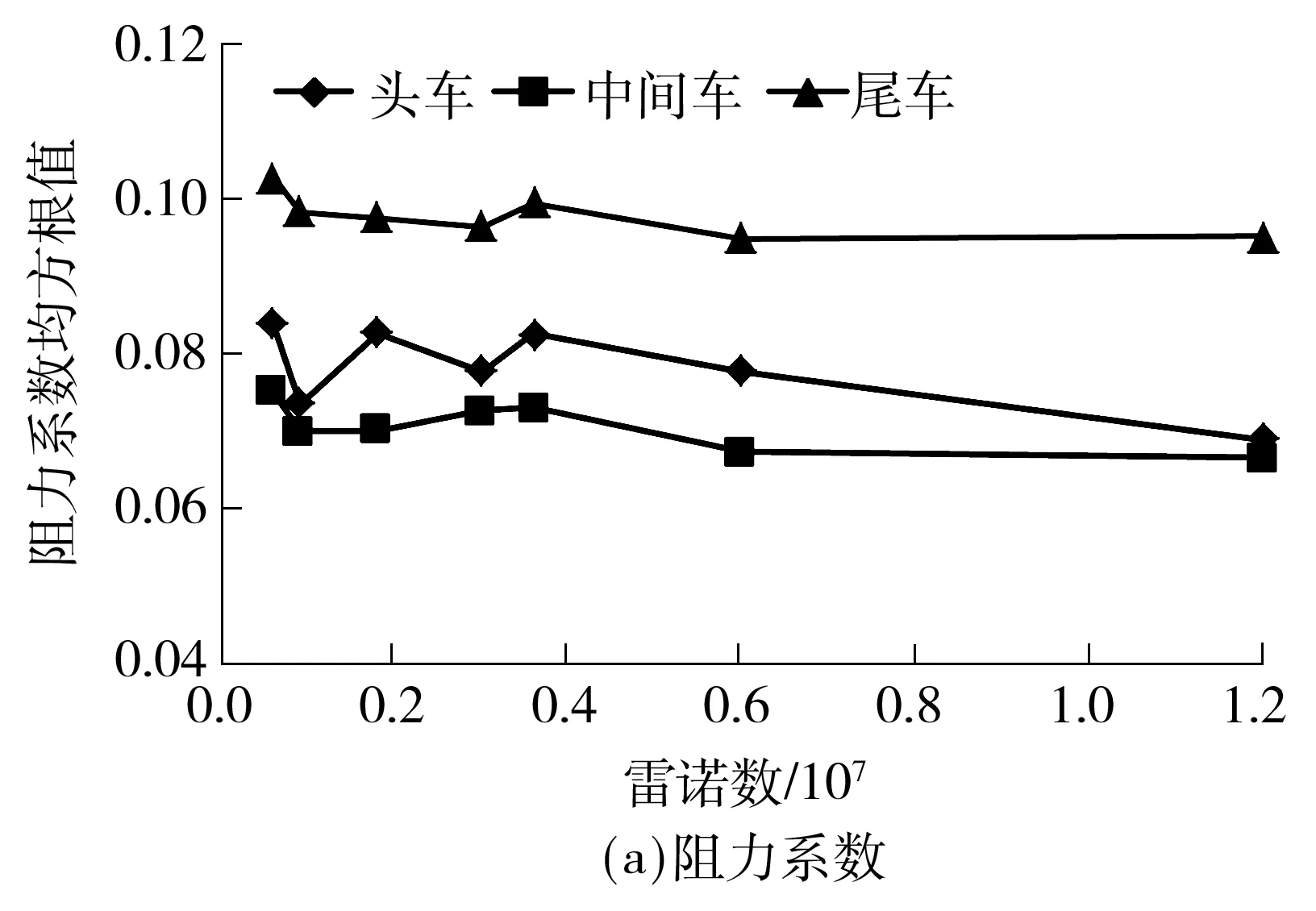
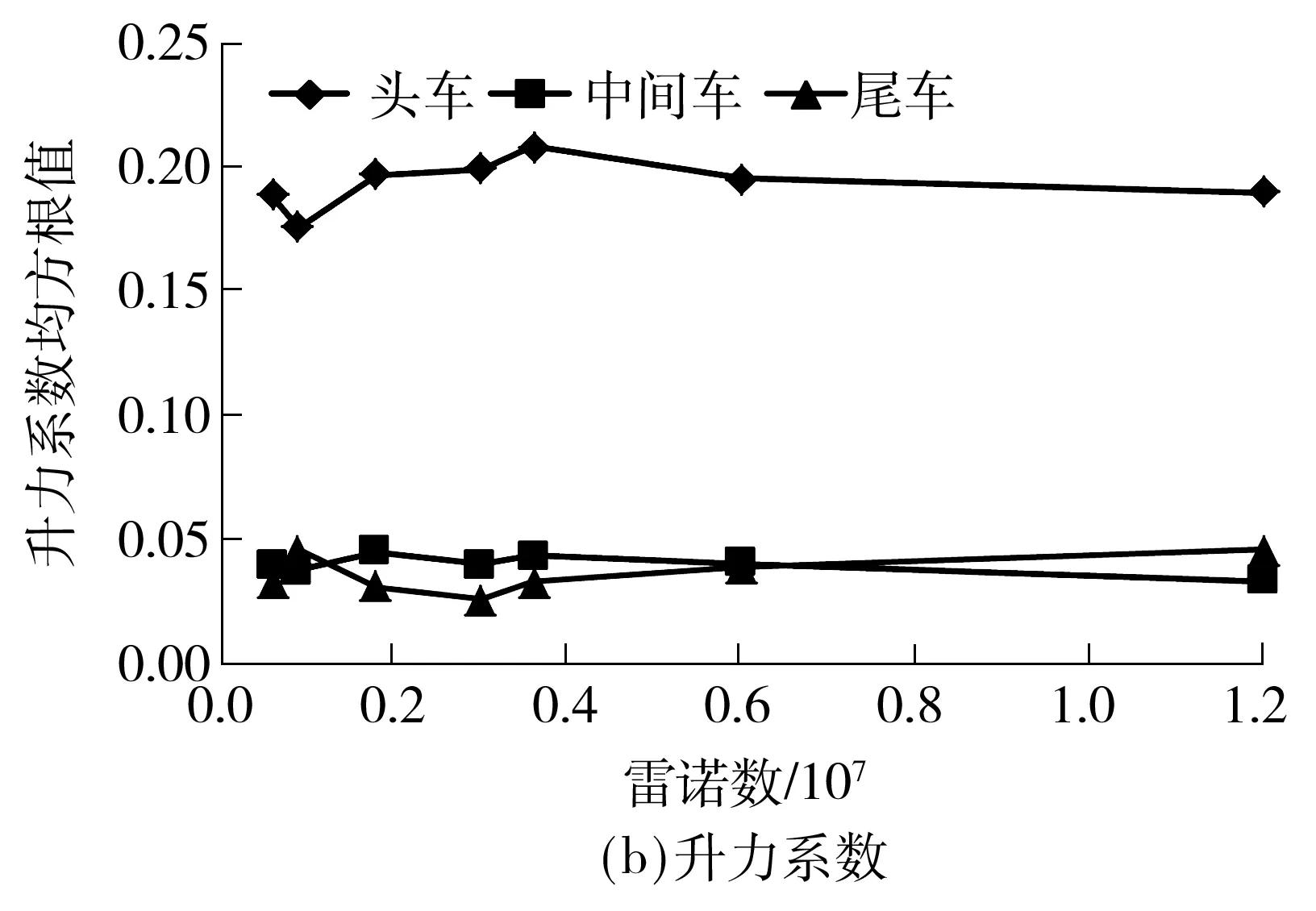
图7　列车气动力系数均方根随雷诺数的变化

Fig.7RSM of train’ unsteady aerodynamic force coefficient changing with Reynolds number

为便于分析不同雷诺数下列车的非定常气动力振动程度，采用非定常气动力系数的标准差值来对比分析列车非定常气动力的雷诺数效应.

图8为列车阻力系数和升力系数标准差值随雷诺数的变化曲线.从图中可知，随雷诺数增大，列车各节车气动阻力系数和升力系数基本呈现减小趋势，且波动明显.列车气动力变化是受涡脱和周围流场中湍流共同作用所致，由于尾涡包含的能量较大，且对尾车影响最大，导致尾车气动力的标准差值相对较大；头车和中间车主要受小涡脱落和湍流的影

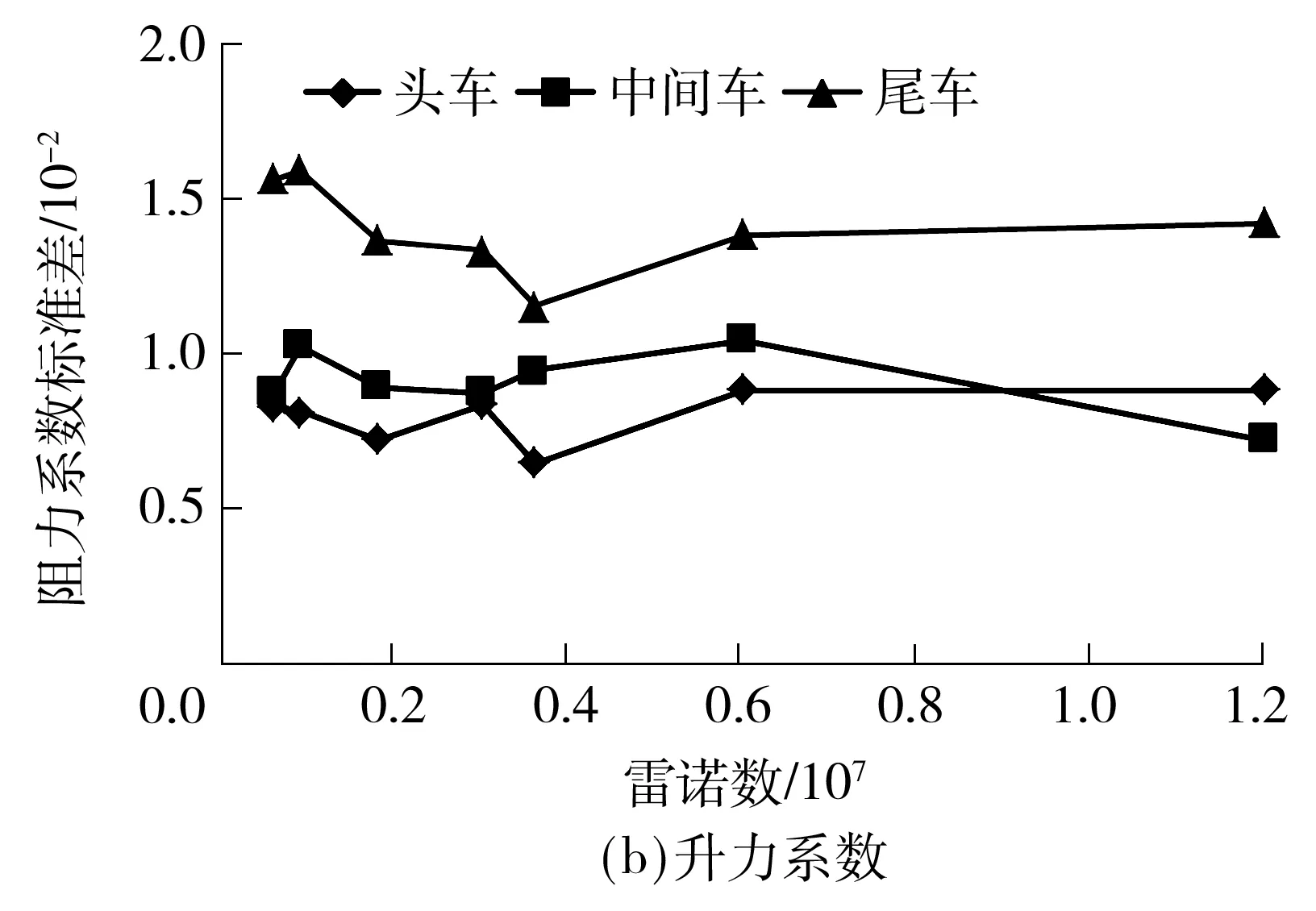
图8　列车气动力系数标准差随雷诺数变化

Fig.8SD of aerodynamic force coefficient changing with Reynolds number

响，呈现出的气动力标准差值较小.

图9为不同雷诺数下列车各节车阻力系数和升力系数的功率谱密度.从图中可知：不同雷诺数下，列车各节车气动阻力系数和升力系数均存在显著差异，雷诺数越大，气动力系数功率谱密度越小；不同雷诺数下气动力系数主频差距明显，但无明显规律.

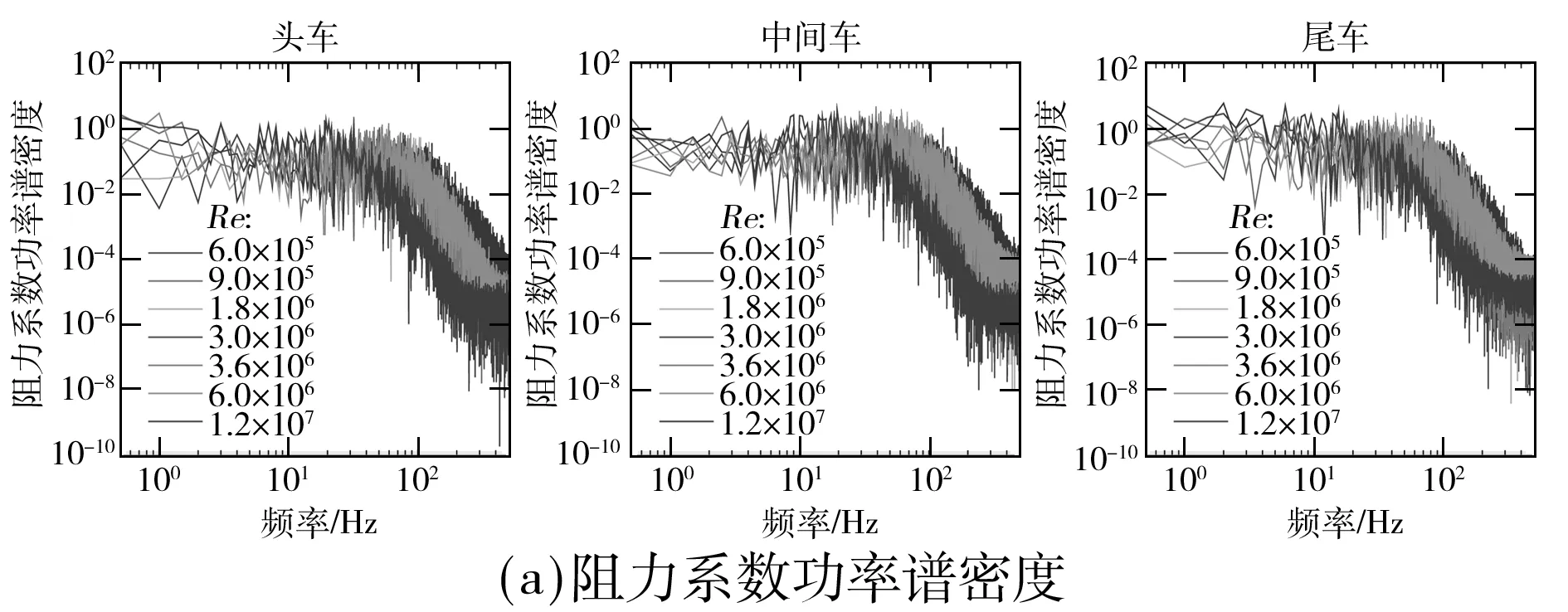
图9　列车气动力系数功率谱密度

3.2气动力振动特性的尺度效应

表1为雷诺数为0.9×106和1.8×106下，不同缩比尺度和来流速度时的列车气动阻力系数均方根值.不同缩比尺度下，通过改变来流速度来达到相同雷诺数.从表1中数据可知：雷诺数为0.9×106时，两种缩比尺度下，头车气动阻力系数接近，不超过1%；中间车和尾车气动阻力系数差距较大，在10%左右.雷诺数为1.8×106时，两种缩比尺度下，头车和中间车气动阻力系数均相差较大，在6%以上，尾车相差不超过4%.对比表1中数据可知，随雷诺数增大，列车气动阻力系数均方根值差距呈现减小趋势，即列车尺度效应减弱.

表2为雷诺数为0.9×106和1.8×106下，不同缩比尺度和来流速度时的列车气动升力系数均方根值.从表2中数据可知：雷诺数为0.9×106时，两种缩比尺度下，头车气动阻力系数接近，不超过3%；中间车相差22%左右；尾车差距较大，在67%左右.雷诺数为1.8×106时，两种缩比尺度下，头车气动阻力系数相差不超过2.3%；中间车相差不超过26%；尾车相差不超过16%.对比表2中数据可知：随雷诺数增大，列车气动升力尺度效应减弱；与气动阻力相比，列车气动升力尺度效应更加显著.

表3为雷诺数为0.9×106和1.8×106下，不同缩比尺度和来流速度时的列车气动阻力系数标准差.从表3中数据可知：雷诺数0.9×106时，两种缩比尺度下，列车气动阻力系数波动显著，头车和尾车的气动阻力系数标准差相差28%左右，中间车相差42%左右；雷诺数为1.8×106时，两种缩比尺度下，头车气动阻力系数标准差相差不超过3%，中间车和尾车相差不超过8%.对比表3中数据可知，列车尺度效应对列车的非定常气动阻力波动影响明显，随雷诺数增大，列车气动阻力波动程度减小，即尺度效应减弱.

表1　列车气动阻力系数均方根

表2　列车气动升力系数均方根

表3　列车气动阻力系数标准差

表4为雷诺数为0.9×106和1.8×106下，不同缩比尺度和来流速度时的列车气动升力系数标准差.从表4中数据可知：雷诺数为0.9×106时，两种缩比尺度下，列车气动阻力系数波动显著，头车和中间车的气动升力系数标准差相差50%～60%，尾车相差20%左右；雷诺数1.8×106时，两种缩比尺度下，头车气动阻力系数标准差相差1%左右，中间车相差不超过5%，尾车相差不超过9%.综合以上可知：相比非定常阻力而言，列车非定常气动升力的尺度效应更加显著；随雷诺数增大，列车气动升力尺度效应减弱.

图10为Re=0.9×106时列车阻力系数和升

表4　列车气动升力系数标准差

力系数的功率谱密度.列车各节车气动力振动主要以低频为主，在低频范围内，1∶10缩比模型的气动力振动功率谱密度相对1∶20缩比模型的要大，而在高频范围内，1∶20缩比模型的气动力振动功率谱密度要比1∶10缩比模型的大.列车模型的尺度效应不改变列车气动力以低频为主的振动特性，但是对气动力振动主频及其功率谱密度有显著影响.

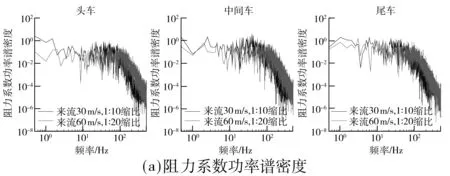
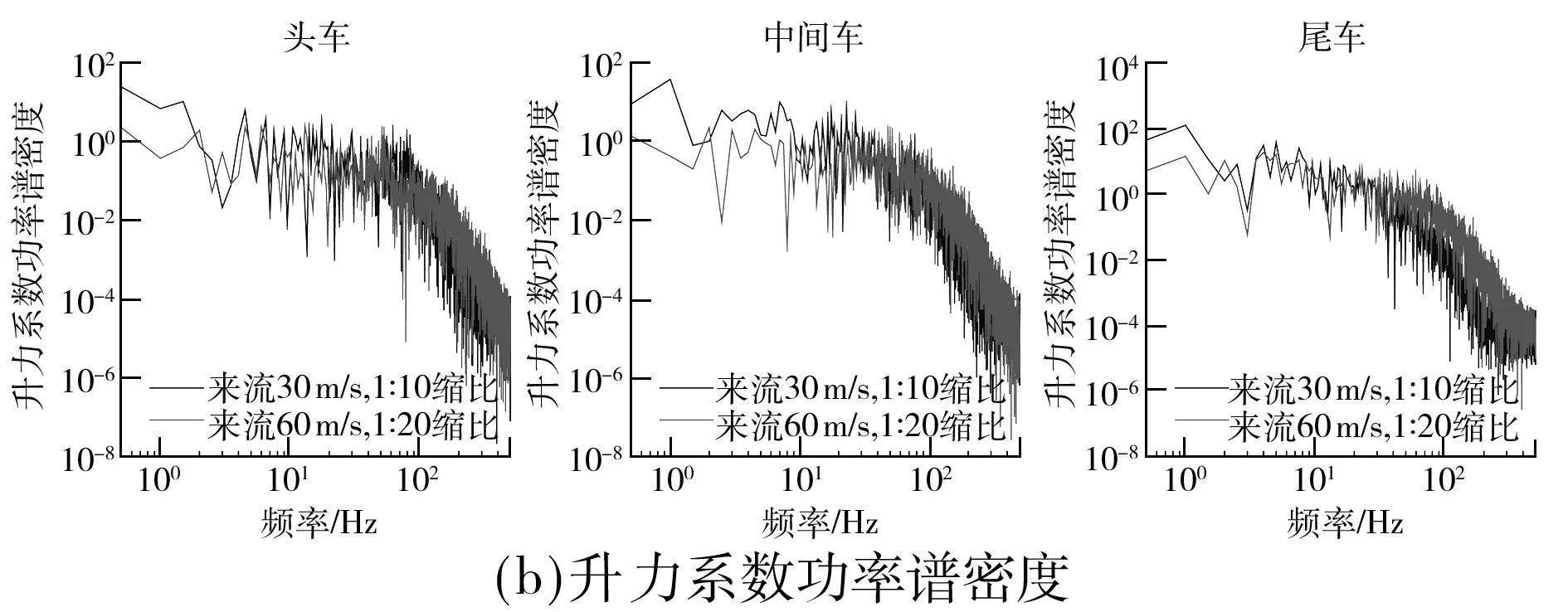
图10　列车气动力系数功率谱密度(Re=0.9×106)Fig.10　PSD of train’s aerodynamic force coefficient(Re=0.9×106)

图11为Re=1.8×106时列车阻力系数和升力系数的功率谱密度.与Re=0.9×106时的列车气动力振动特性相比，Re=1.8×106时的列车气动力振动特性的尺度效应同样明显，且分布规律基本一致.

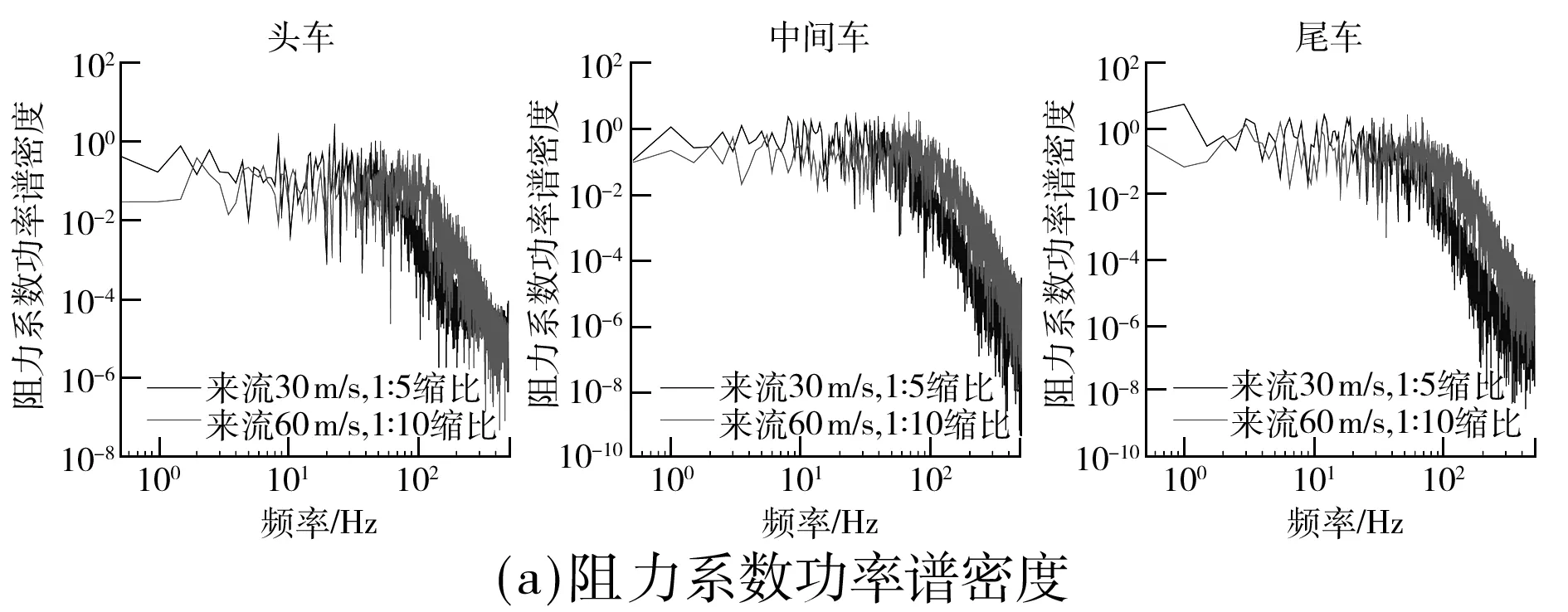
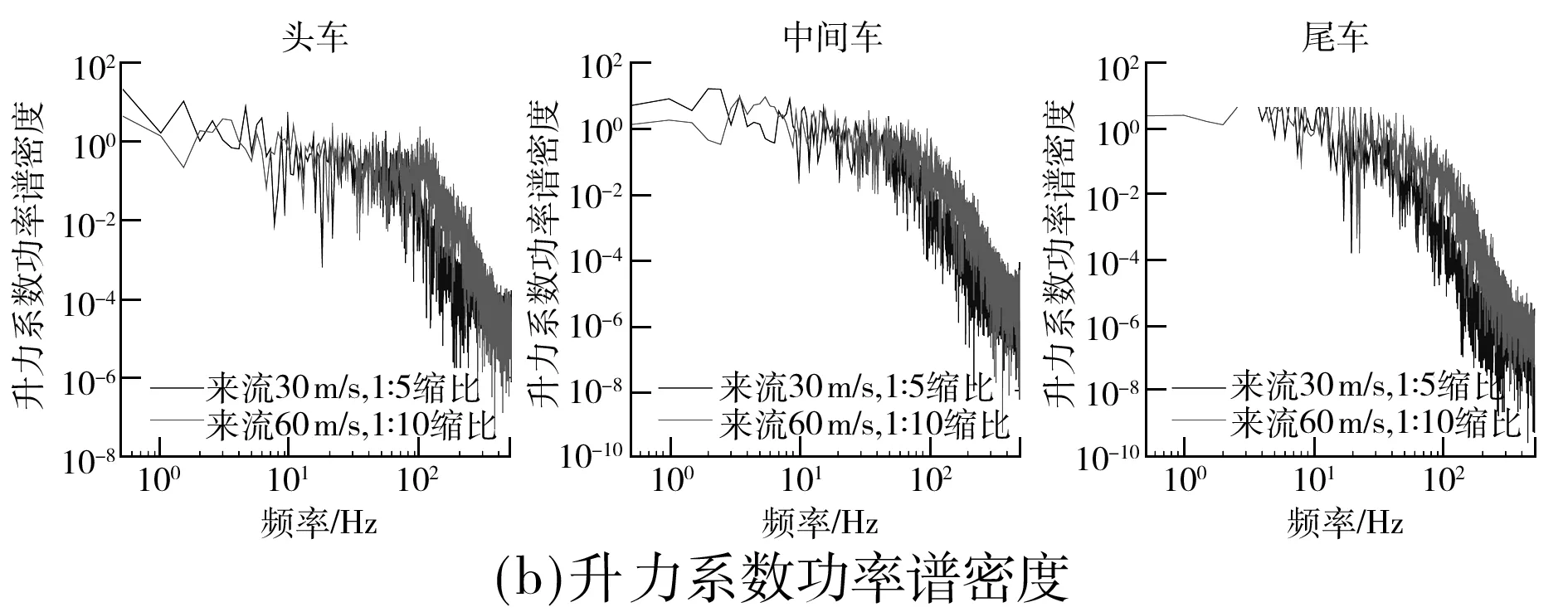
图11　列车气动力系数功率谱密度(Re=1.8×106)Fig.11　PSD of train’s aerodynamic force coefficient(Re=1.8×106)

4　结论

文中通过改变改变模型缩比尺度和来流速度来研究列车非定常气动特性的雷诺数效应和尺度效应，得到以下结论：列车气动力振动明显；随雷诺数增加，各节车气动阻力系数和升力系数的均方根值均基本呈现减小趋势，但波动明显.随雷诺数增大，列车各节车气动阻力系数和升力系数标准差均先减小后增大，且波动明显.不同雷诺数下，列车各节车气动阻力系数和升力系数均存在显著差异，雷诺数越大，气动力系数功率谱密度越小；不同雷诺数下气动力系数主频差距明显，但无明显规律.列车气动力尺度效应显著，随雷诺数增大，列车气动力尺度效应减弱；相比列车气动阻力，列车气动升力尺度效应更加显著.列车尺度效应对列车非定常气动阻力波动影响明显，随雷诺数增大，列车气动阻力波动程度减小，即尺度效应减弱.相比非定常阻力而言，列车非定常气动升力的尺度效应更加显著；随雷诺数增大，列车气动升力尺度效应减弱.尺度效应不改变列车气动力以低频为主的振动特性，但是对气动力振动主频及其功率谱密度有显著影响.尺度效应不改变列车气动力功率谱密度的分布规律.

[1]田红旗.中国列车空气动力学研究进展 [J].交通运输工程学报,2006,6(1)：1- 9.

TIAN Hong-qi.Study evolvement of train aerodynamics in China [J].Journal of Traffic and Transportation Engineering,2006,6(1)：1- 9.

[2]田红旗.中国恶劣风环境下铁路安全行车研究进展 [J].中南大学学报(自然科学版),2010,41(6)：2435- 2443.

TIAN Hong-qi.Research progress in railway safety under strong wind condition in China [J].Journal of Central South University(Science and Technology),2010,41(6):2435- 2443.

[3]BACKER C.The flow around high speed trains [J].Journal of Wind Engineering & Industrial Aerodynamics,2010,98(6/7)：277- 298.

[4]BELL J R,BURTON D,THOMPSON M C,et al.Wind tunnel analysis of the slipstream and wake of a high-speed train [J].Journal of Wind Engineering & Industrial Aerodynamics,2014(134)：122- 138.

[5]BELL J R,BURTON D,THOMPSON M C,et al.Moving model analysis of the slipstream and wake of a high-speed train [J].Journal of Wind Engineering & Industrial Aerodynamics,2015(136)：127- 137.

[6]FLYNN D,HEMIDA H,SOPER D,et al.Detached-eddy simulation of the slipstream of an operational freight train [J].Journal of Wind Engineering & Industrial Aerodynamics,2014(132):1- 12.

[7]任尊松,刘志明.高速动车组振动传递及频率分布规律 [J].机械工程学报,2013,49(16):1- 7.

REN Zun-song LIU Zhi-ming.Vibration and frequency domain characteristics of high speed EMU [J].Journal of Mechanical Engineering,2013,49(16):1- 7.

[8]宁迎智,周小林,徐庆元,等.基于小波的轨道不平顺和车体振动响应分析 [J].铁道科学与工程学报,2013,10(3)：28- 32.

NING Ying-zhi，ZHOU Xiao-lin，XU Qing-yuan，et al.Analysis of track irregularity and car-body vibration response based on wavelet transform [J].Journal of Railway Science and Engineering,2013,10(3)：28- 32.

[9]刘加利,于梦阁,张继业,等.基于大涡模拟的高速列车横风运行安全性研究 [J].铁道学报,2011,33(4)：13- 21.

LIU Jia-li,YU Meng-ge,ZHANG Ji-ye,et al.Study on running safety of high-speed train under crosswind by large eddy simulation [J].Journal of the China Railway Society,2011,33(4)：13- 21.

[10]刘加利,张继业,张卫华.基于大涡模拟的横风下高速列车非定常气动载荷特性 [J].铁道学报,2013,35(6)：13- 21.

LIU Jia-li,ZHANG Ji-ye,ZHANG Wei-hua.Study on characteristics of unsteady aerodynamic loads of a high-speed train under crosswinds by large eddy simulation [J].Journal of the China Railway Society,2013,35(6)：13- 21.

[11]杨志刚,马静,陈羽,等.横风中不同行驶工况下高速列车非定常空气动力特性 [J].铁道学报,2010,32(2)：18- 23.

YANG Zhi-gang,MA Jing,CHEN Yu,et al.The unsteady aerodynamic characteristics of a high-speed train in different operating conditions under cross wind [J].Journal of the China Railway Society,2010,32(2)：18- 23.

[12]马静,张杰,杨志刚.横风下高速列车非定常空气动力特性研究 [J].铁道学报,2008,30(6)：109- 114.

MA Jing,ZHANG Jie,YANG Zhi-gang.Study on the unsteady aerodynamic characteristics of a high-speed train under cross wind [J].Journal of the China Railway Society,2008,30(6)：109- 114.

[13]郭迪龙,姚拴宝,刘晨辉,等.高速列车受电弓非定常气动特性研究 [J].铁道学报,2012,34(11)：16- 21.

GUO Di-long,YAO Shuan-bao,LIU Chen-hui,et al.Unsteady aerodynamic characteristics of high-speed pantograph [J].Journal of the China Railway Society,2012,34(11)：16- 21.

[14]郗艳红,毛军,高亮,等.横风作用下高速列车转向架非定常空气动力特性 [J].中南大学学报(自然科学版),2014,45(5)：1705- 1714.

XI Yan-hong,MAO Jun,GAO Liang,et al.Aerodynamic force/moment for high-speed train bogie in crosswind field [J].Journal of Central South University(Science and Technology),2014,45(5)：1705- 1714.

[15]BAKER C J,BROCKIE N J.Wind tunnel tests to obtain train aerodynamic drag coefficients：Reynolds number and ground simulation effects [J].Journal of Wind Enginee-ring & Industrial Aerodynamics,1991,38(1)：23- 28.

[16]CHELI F,GIAPPINO S,ROSA L,et al.Experimental study on the aerodynamic forces on railway vehicles in presence of turbulence [J].Journal of Wind Enginee-ring & Industrial Aerodynamics,2013,123(6)：311- 316.

[17]BOCCIOLONE Marco,CHELI F,CORRADI Roberto,et al.Crosswind action on rail vehicles：wind tunnel experimental analyses [J].Journal of Wind Engineering & Industrial Aerodynamics,2008,96(5)：584- 610.

[18]CHELI F,CORADI R,SABBIONI E,et al.Wind tunnel tests on heavy road vehicles：cross wind induced loads—Part 1 [J].Journal of Wind Engineering & Industrial Aerodynamics,2011,99(10)：1000- 1010.

[19]陶文铨.数值传热学 [M].第2版.西安:西安交通大学出版社,2001.

[20]SAGAUT P.Large eddy simulation for incompressible flows an introduction [J].Scientific Computation,2001,12(12)：1745- 1746.

[21]BERSELLI L C,ILIESCU C,LAYTON W J，et al.Mathematics of large eddy simulation of turbulent flows [M].Berlin:Springer Press,2005.

[22]ZHANG Bin,WANG Tong,GU Chuan-gang,et al.An adaptive control strategy for proper mesh distribution in large eddy simulation [J].Journal of Hydrodynamics,2010,22(6)：865- 871.

[23]FRISCH U.Turbulence,the legacy of A N kolmogorov [M].Cambridge:Cambridge University Press,1995.

[24]KOLMOGOROV A N.The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers [J].Proceedings：Mathematical and Physical Sciences,1991,434(1890)：9- 13.

[25]高广军,田红旗,张健.横风对双层集装箱平车运行稳定性的影响 [J].交通运输工程学报2004,4(2):45- 48.

GAO Guang-jun,TIAN Hong-qi,ZHANG Jian.Crosswind affection on double container train [J].Journal of Traffic and Transportation Engineering,2004,4(2)：45- 48.

[26]RAGHUNATHAN R S,KIM H D,SETOGUCHI T.Aerodynamics of high-speed railway train [J].Progress in Aerospace Sciences,2002,38(6/7)：469- 514.

[27]夏超,单希壮,杨志刚,等.不同湍流模型在列车外流场计算中的比较 [J].同济大学学报(自然科学版),2014,42(11):1687- 1693.

XIA Chao,SHAN Xi-zhuang,YANG Zhi-gang,et al.A comparative study of different turbulence models in computation of flow around simplified train [J].Journal of Tongji University(Science and Technology),2014,42(11)：1687- 1693.

[28]梁建永,梁军,范士杰,等.轿车外流场CFD分析中常用k-ε湍流模型的对比 [J].汽车工程,2008,30(10)：846- 852.

LIANG Jian-yong,LIANG Jun,FAN Shi-jie,et al.Comparison amongk-εturbulence models in CFD analysis on flow field around a car [J].Automotive Engineering,2008,30(10)：846- 852.

[29]Zhang J,Li J,Tian H,et al.Impact of ground and wheel boundary conditions on numerical simulation of the high-speed train aerodynamic performance [J].Journal of Fluids & Structures,2016,61(4)：249- 261.

s: Supported by the National Natural Science Foundation of China(U1134203，U1334205) and the Natural Science Foundation of Hunan Province(14JJ3028)

Reynolds Number Effect of Unsteady Aerodynamic Force and Spectrum Characteristics of High-Speed Train

NIUJi-qiangLIANGXi-fengZHOUDanLIUFeng

(School of Traffic and Transportation Engineering∥Key Laboratory of Traffic Safety on Track of the Ministry of Education,Central South University, Changsha 410075, Hunan, China)

In the investigation, the unsteady flow fields around the train at different model scales and different flow velocities are solved by means of the delayed detached eddy simulation (DDES) method of the realizableκ-εturbulence model. Then, the Reynolds number effect and scale effect of the unsteady aerodynamic characteristics of the train are discussed by changing the model scale and the flow velocity. The results show that (1) with the increase of the Reynolds number, the RMS (Root Mean Square) of the aerodynamic drag coefficient of the train decreases but fluctuates obviously; (2) as the Reynolds number increases, the SD (Standard Deviation) of the aerodynamic drag coefficient and lift coefficient of the train first decrease and then increase, and also fluctuate obviously; (3) the PSD (Power Spectrum Density) of aerodynamic coefficients decreases with the increase of the Reynolds number; (4) the Reynolds number can affect the basic frequency of aerodynamic coefficients, but without obvious rules; (5) the aerodynamic force of trains brings about a significant scale effect; (6) with the increase of the Reynolds number, the scale effect of the aerodynamic force decreases, and the scale effect of the lift force becomes relatively significant; (7) the vibration scale effect of the unsteady drag and lift decreases with the increase of the Reynolds number, and the vibration scale effect of the unsteady lift force is more obvious than that of the unsteady drag; and (8) the scale effect has no effect on the vibration characteristics based on low frequencies and the PSD distribution of the aerodynamic force, but greatly affects the vibration frequency of the aerodynamic force and its PSD.

high-speed train; unsteady aerodynamic force;reynolds number effect; scale effect; power spectrum density

2015- 08- 24

高铁联合基金资助项目(U1134203,U1334205);湖南省自然科学基金资助项目(14JJ3028);湖南省研究生科研创新计划资助项目(CX2015B046)

牛纪强(1988-),男,博士生,主要从事列车空气动力学研究.E-mail:jiqiang_niu@163.com

1000- 565X(2016)08- 0082- 09

U 27;V 211

10.3969/j.issn.1000-565X.2016.08.013