基于压缩感知的条带SAR缺失数据恢复成像方法

段化军，朱岱寅，李　勇，吴　迪

（南京航空航天大学电子信息工程学院雷达成像与微波光子技术

教育部重点实验室，江苏　南京 210016）

基于压缩感知的条带SAR缺失数据恢复成像方法

段化军，朱岱寅，李勇，吴迪

（南京航空航天大学电子信息工程学院雷达成像与微波光子技术

教育部重点实验室，江苏南京 210016）

针对条带模式合成孔径雷达回波缺失数据，提出了一种利用压缩感知恢复缺失数据并成像的方法。将条带数据分块为多个子孔径数据，对子孔径利用压缩感知恢复缺失数据并拼接得到条带数据，缩短了整个数据的恢复时间，推导了压缩感知处理的基矩阵和测量矩阵。运用最大似然估计的特征向量方法（eigenvector method for maximum likelihood estimation，EMMLE）实现了子孔径缺失数据的自聚焦，满足了压缩感知对图像的稀疏要求。利用压缩感知恢复完整的相位误差信号，解决了子孔径补偿相位误差数据的拼接问题。最后通过对恢复的雷达回波数据成像并自聚焦校正了距离徙动，得到了聚焦良好的完整图像，提高了缺失数据的成像质量。

合成孔径雷达；压缩感知；最大似然估计的特征向量方法；数据恢复

网址：www.sys-ele.com

0　引　言

合成孔径雷达（synthetic aperture radar，SAR）能够全天候和全天时地获取高分辨地面图像，在军事和民用领域都获得了广泛应用，越来越受到人们的重视。在实际工作中，雷达所发射和接收的电磁波很容易受到外界的干扰，造成雷达回波脉冲的损坏或缺失。将损坏或缺失的脉冲数据置零，采用传统的雷达成像方法成像，会造成图像质量一定程度的下降［1 2］。对机载雷达而言，提高缺失数据的成像质量具有重要的研究和应用价值［3-4］。

对于缺失数据恢复方法，第1类是插值方法，可以利用缺失数据两侧完整的数据通过插值恢复中间缺失的数据［5］，但是当数据的频谱存在混叠或者连续缺失数据较多时，该方法对缺失数据恢复的效果不理想；第2类是线性预测和递推的方法［6-8］，该方法通过预测和递推利用完整数据实现缺失数据的恢复，但该类算法对预测模型和信杂比比较敏感，当缺失数据较多时，其对缺失数据的恢复会成指数级衰减，导致恢复效果不理想；第3类是谱估计方法，比较典型的是缺失数据幅度相位估计（gapped-data amplitude and phase estimation，GAPES）方法［1-2，9-10］和丢失数据的迭代自适应 恢复方 法（missing data iterative adaptive approach，MIAA）［11］方法等，该类方法是一种基于谱估计非参数化的缺失数据恢复方法，由于其具有鲁棒性高，不受模型参数的影响等优点，对于一维信号或者小场景数据具有较强的恢复能力，但该方法在信号恢复时，需要进行大量的矩阵求逆运算且需要多次迭代，对于SAR数据来说，其运算量超出了目前硬件的运算能力，不适合两维大数据量的SAR成像恢复算法。

压缩感知（compressed sensing，CS）［12-15］是一种新兴的信号重构恢复算法，只要信号满足在某一个域稀疏的条件，就能以远低于奈奎斯特采样定律的采样频率对时域信号进行采样。通过近似重构算法，能够以极高的概率或者完全重构恢复原始信号。CS理论提出以后，很多学者研究了CS在雷达距离向稀疏频率［16-18］和方位向脉冲稀疏采样数据［19-21］的成像方法。文献［22］是两维稀疏采样，采用对场景距离向分块处理，降低了稀疏矩阵的复杂度，减轻了运算负担，得到场景的距离向分块图像后再进行图像拼接得到完整的图像。以上都是基于CS聚束模式成像方法的研究，聚束模式数据量少，目前的硬件条件可以承受重构过程的运算量。文献［23］是针对条带模式稀疏孔径SAR压缩感知处理方法的研究，但其基本成像方法是基于距离多普勒（range-Doppler，R-D）算法，只校正了距离走动，而没有校正距离弯曲，且没有考虑相位误差补偿的问题，影响了图像的分辨率。

目前，对于条带随机缺失数据，其处理难度主要包括：一是条带模式数据量大，图像重构时计算量超过了目前硬件运算能力；二是条带模式SAR由于孔径长度长，处理过程中需要考虑距离徙动校正的问题，否则会影响最后的成像分辨率；三是相位误差的校正问题，由于缺失数据的脉冲间隔时间非均匀，不能变换到频域处理，所以传统自聚焦方法的聚焦效果受到了一定的限制；四是SAR信号属于两维线性调频信号，如果直接对原始信号在频域重构恢复缺失数据，线性调频信号在频谱上占据的频带较宽，不满足CS的稀疏要求。

针对以上问题，本文提出了利用CS恢复缺失数据的方法，一是通过将原始缺失条带数据分成多个子孔径，对每个子孔径分别进行恢复然后进行拼接得到条带数据，可以降低数据的计算量，提高计算效率；二是对每个子孔径通过预处理将数据变换到图像域利用CS重构成像，然后对重构后的图像恢复原始数据；三是子孔径在CS重构图像之前，对缺失数据进行自聚焦处理，使图像满足稀疏要求；四是利用CS对补偿的相位误差信号进行恢复，保证自聚焦之后恢复数据的子孔径拼接不会出现重影；五是对恢复的数据利用传统的chirp-scaling算法［24］和自聚焦处理［25］，解决了缺失数据距离徙动校正和图像的自聚焦问题，提高了缺失数据的图像质量。通过直升机实测数据证明了本文所述方法的有效性和实用性。

1　基于CS的数据恢复方法

1.1子孔径划分

由于条带数据的脉冲数远远超过了CS的数据恢复处理能力，所以首先把条带数据分块为多个互不重叠的子孔径数据。根据条带和聚束模式的数据特点，将原始的数据分块为聚束算法可以处理的多个子孔径数据［26］。其分块的数据形式如图1所示。

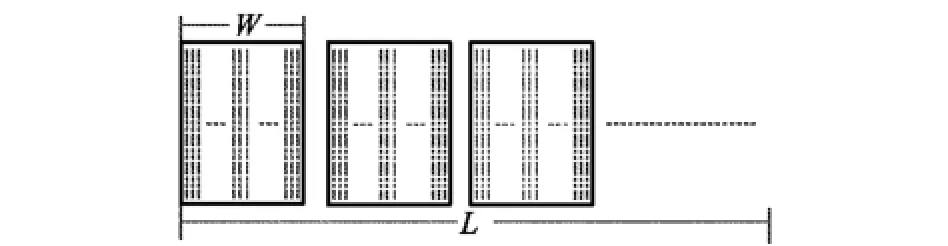
图1　原始数据分块子孔径示意图

图1中，W代表子孔径的长度，L为整个条带数据的长度，子孔径的数目为J=L/W。

1.2子孔径预处理

每个子孔径不能直接利用CS进行缺失数据的恢复，需对每个子孔径预处理，将数据变换到图像域重构成像恢复，其过程如下。

雷达发射线性调频（linear frequency modulated，LFM）信号，目标反射后的二维回波信号为

式中，rect（·）表示矩形窗函数；t为方位慢时间；Ta为子孔径方位孔径时间；τ为距离快时间；c为电波传播速度；Tr为脉冲持续时间；k为调频斜率；fc为载频；Ra为目标点与天线相位中心的距离。

对式（1）距离向做傅里叶变换得到

对子孔径回波信号进行匹配滤波和运动补偿，使子孔径场景中心点的回波相位为零，即式（2）乘以式（3）参考函数。

式中，R0为子孔径成像区域中心与天线相位中心的距离，得到的信号形式为［2-28］

式中，B=K Tr为发射信号带宽。

式（4）距离向逆傅里叶变换得到

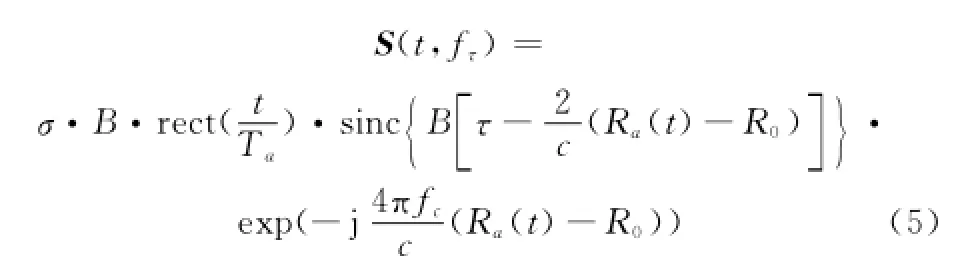
此时，子孔径距离向脉压完成，方位向利用CS重构成像。

1.3子孔径CS重构成像

1.3.1CS原理

假设复信号S∈CN，可以用正交基矩阵Φ=｛φ1，φ2，…，φN｝稀疏表示S=Φθ，θ为稀疏向量。

观测矩阵A∈CM×N（M＜N），可以得到测量信号r= AS。若Ψ=AΦ满足有限等距性质（restricted isometry property，RIP）准则，则可以通过求最优解的方法精确或者近似精确的恢复原始信号［29］，表示为

式中，ε为噪声容限；θ′为稀疏向量估值。

1.3.2子孔径缺失数据恢复

如果场景中某些区域的雷达回波反射强度明显强于场景中其他区域或者场景区域在整个成像区域内占据很少的一部分，则可认为场景稀疏［30 31］。由于场景在方位向频域成像且其频域满足稀疏要求，本文利用傅里叶基作为基矩阵。

假设子孔径数据的方位向脉冲总数为N，可利用的脉冲数为M（M＜N），则缺失的脉冲数为N-M。首先构造方位向基矩阵φ=｛φ0，φ1，…，φN-1｝N×N，式中

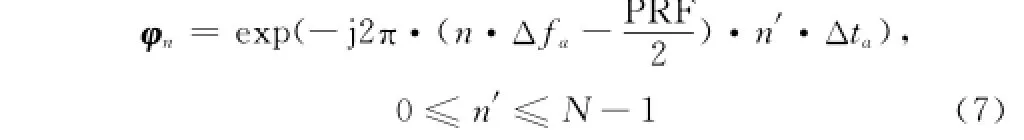
式中，φn为列向量；PRF为脉冲重复频率；为方位向频率间隔；脉冲重复间隔。

方位向测量矩阵A是从N×N维单位矩阵抽取M行构成的M×N维矩阵，其中M行的位置与回波数据中可利用脉冲数据的位置对应。因此每一距离单元上方位向的观测向量Sa可以表示为

式中，θa为方位向的稀疏向量，即每一距离单元上的方位向在频域的重构图像，CS重构可以代替式（5）的方位向傅里叶变换过程。

循环完成对每一个距离单元的重构过程，可以得到各个子孔径的重构图像。

对CS重构的图像方位向做逆傅里叶变换，可以得到距离压缩之后的数据，此时的数据已经将缺失的脉冲数据恢复，方位向数据变成了完整数据。再将所得的结果在距离向做傅里叶变换，并乘式（9）信号。

对所得结果在距离向做逆傅里叶变换，就可以得到各个完整子孔径的数据。

1.3.3子孔径拼接

由于原始的数据在进行子孔径分块时，子孔径之间没有重叠，将各个子孔径数据按照子孔径划分的顺序直接进行拼接得到全孔径条带数据。

2　子孔径自聚焦

在载机的实际工作中，往往存在运动误差，这将造成较大的相位误差。如果不补偿相位误差，图像会在方位向的散焦，即使目标场景是稀疏的，重构图像也并不满足CS理论对于稀疏度的要求，CS重构图像也就无从谈起，所以在子孔径CS重构图像之前，需对子孔径数据进行自聚焦处理。

目前，应用比较多的自聚焦算法主要是相位梯度自聚焦（phase gradient autofocus，PGA）算法［32］。由于其不受信号模型的影响、鲁棒性比较高而得到了研究人员的重视。但是对于方位向缺失数据来说，数据方位向是稀疏的，不能直接变换到频域。如果对缺失数据补零然后变换到频域，这时得到的图像会明显发散，PGA算法聚焦效果会不理想。

本文采用了最大似然估计的特征向量方法（eigenvector method for maximum likelihood estimation，EMMLE）［33 34］估计子孔径的相位误差，该方法利用了所有脉冲数据估计相位误差，不需要加窗就能得到良好的聚焦效果。对于缺损数据的EMMLE自聚焦算法需要做一些改进，其过程如下：

步骤1对方位向缺失的数据补零，做傅里叶变换，成一个初像。

步骤2将每一个距离门内的强散射点移动到多普勒零点，对移位后的数据进行逆傅里叶变换，将图像变换回数据域，将补零位置的数据去除。

步骤4提取特征向量的相位部分并将缺失数据中的误差相位补偿掉。

步骤5重复步骤1～步骤4，直到达到终止迭代的条件。

通过以上步骤可以补偿数据中的相位误差，使重构图像的稀疏性只和场景的稀疏有关，而不受相位误差的影响，保证了CS重构图像结果的准确性。

3　相位误差信号的恢复

各个子孔径在做自聚焦时，子孔径间存在未知的线性相位，如果对自聚焦之后恢复的子孔径数据直接进行拼接，会造成条带数据图像的重影［25］，所以在子孔径数据拼接之前，每个子孔径数据要将自聚焦补偿的相位误差信号恢复，才能保证拼接数据的正确和完整。

对于原始缺失数据，其相位误差信号是非连续的。通过压缩感知已将缺失的数据恢复完整，所以不能直接将非连续的相位误差信号补偿回恢复的连续数据中，需要利用非连续的相位误差信号恢复连续的相位误差信号，本文提出了利用压缩感知恢复相位误差信号的方法，其过程如下：

取子孔径EMMLE聚焦前后同一个距离波门上的信号进行傅里叶变换并共轭相乘，得到缺失数据的相位误差信号为

式中，S1和S2分别表示同一距离波门聚焦前后对应的信号；FFT（·）表示对括号里的内容作傅里叶变换；conj（·）表示对括号里的内容求共轭。

Θ在频域仍然是稀疏信号，如图2所示。

图2　相位误差的频域信号

通过第1.3.2节所介绍的基矩阵φ和测量矩阵A，可以对Θ在频域稀疏重构。相位误差信号Θ可以表示为

式中，φ为Θ的频域稀疏向量。对φ稀疏重构后，对φ做逆傅里叶变换，可得到子孔径完整的相位误差信号。

图3和图4分别是缺失数据和CS恢复的相位误差信号。从图3可以得到，由于原始数据中缺失脉冲位置的数据不连续，所以图3中的相位误差是非连续的。

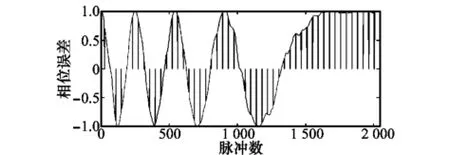
图3　缺失数据的相位误差信号

图4　CS恢复的相位误差信号

通过比较图3和图4可以看出，通过CS恢复的相位误差信号由不连续的相位误差信号变为连续的相位误差信号。

4　算法流程

本文所述对缺失数据利用CS恢复并成像方法的处理流程如图5所示。

图5本文所述方法的数据处理流程图

5　实测数据处理结果及分析

5.1实测处理结果

本文以国内某型号直升机机载SAR实测数据为例，对本文所述方法的处理结果进行分析。雷达主要参数如下：雷达载频fc=10 GHz，信号带宽B=1 GHz，距离向采样率fs= 1.2 GHz，脉冲宽度τ=15μs，脉冲重复频率PRF=2 000 Hz。整个孔径的长度为16 384，分块子孔径长度为2 048。由于该型号直升机雷达位于直升机旋翼的顶端，受旋翼遮挡效应的影响，接收到的回波受到干扰，造成回波数据的缺失。

直升机机载SAR原始的缺失雷达回波数据，如图6所示。

图6原始的缺失回波数据

由图6可以看出，原始回波数据中的暗色条纹就是受干扰的脉冲数据。每个脉冲各距离波门上数据的功率求和，其结果如图7所示。

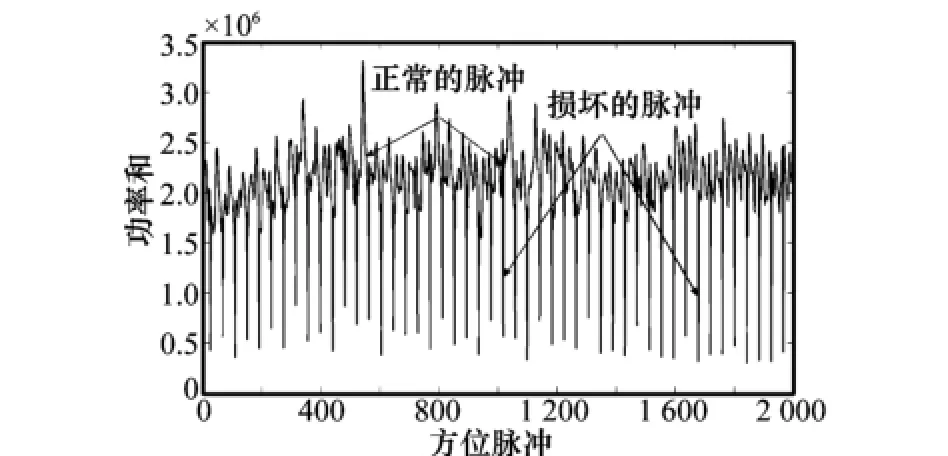
图7　原始回波数据各脉冲回波的功率和

通过图7可以看出，受干扰的脉冲功率明显弱于正常脉冲，将受干扰的脉冲数据置零。

对条带缺失数据进行子孔径分块，利用CS重构的子孔径图像如图8所示。

图8　压缩感知重构的子孔径图像

利用子孔径重构图像恢复的子孔径数据如图9所示。

图9 CS恢复的子孔径数据

通过图9可以看到，子孔径数据中没有损坏的脉冲数据，全部数据得到了恢复。经子孔径数据拼接得到的条带数据如图10所示。

图10　恢复的完整的全孔径数据

通过对比图10和图6可知，原始的缺失数据得到了完整恢复，图6中受干扰数据的暗色条纹在图10中完全消失。

原始缺失数据、插值恢复数据、GAPES恢复数据及本文所述算法恢复数据利用chirp-scaling［24］算法及自聚焦［25］成像结果如图11所示。

图11（a）为原始条带缺失数据的成像结果；图11（b）为通过sinc插值对缺失脉冲数据插值恢复的成像结果；图11（c）为利用缺失数据两侧100个脉冲通过GAPES算法恢复缺失脉冲数据的成像结果；图11（d）为本文所述算法恢复缺失脉冲数据的成像结果；图12通过局部放大图，对4种结果进行对比。

图11条带数据成像结果

图12　条带数据成像结果局部放大图

通过对比图11和图12的4幅图像可以得到，原始回波数据由于脉冲数据的缺失，在成像时其图像质量降低，图像的重影非常明显。插值方法虽然对结果有一定的改善，但还是有重影，图像质量仍达不到要求；GAPES恢复方法由于只采用了缺失脉冲数据两侧100个脉冲对缺失数据进行恢复，其计算量可以承受，但是100脉冲的频谱宽度远远小于点目标整个孔径频谱的宽度，所以GAPES恢复的数据并没有包含缺失数据的全部频谱信息，其成像结果虽然得到了改善，但仍然存在重影，成像质量仍比较低；本文所述方法的图像克服了原始缺失数据的重影问题，图像质量得到了改善，得到聚焦良好的图像。

5.2性能分析

5.2.1图像质量分析比较

下面通过图像熵值定量地评估4幅图像的图像质量，以便更好地评价本文所述算法的性能。二维SAR图像的熵定义为

式中，Na为图像方位向点数；Nr为图像距离向点数；P（i，j）为图像的散射强度密度，其定义为

式中，Q（S）为图像的总能量，其定义为

式中，S（i，j）为图像中每一点的反射强度。对于同样数据的成像结果，图像清晰，其对应的熵值较小，图像模糊，对应的熵值较大。分别计算4幅图像的熵值，结果如表1所示。

表1　图像熵值

通过表1可以看出，本文所提算法处理得到的SAR图像的熵值明显小于其他3幅图像的熵值，证明本文所述算法相比于其他算法对于提高条带缺失数据的成像质量具有更大的效果。

5.2.2运算效率分析比较

下面通过对本文所述算法和GAPES算法运算复杂度的比较，证明本文所述算法的计算效率优于GAPES算法。

本文所述算法的运算复杂度主要取决于压缩感知的重构过程。本文压缩感知重构算法采用的正交匹配追踪（orthogonal matching pursuit，OMP）算法，该算法的运算复杂度为O（p Md）［22，29］，其中p 代表稀疏度并且p≪N，M表示子孔径可利用的脉冲数（M＜N），d表示重构数据的维数，一般与子孔径方位向脉冲总数N相同。子孔径数目为J，距离向采样点数为K，则整个恢复处理的总运算复杂度为JK·O（p Md）。GAPES算法的运算复杂度为m· O（2k N2+k N+N3）［6，35］，其中N表示子孔径方位向脉冲总数，k表示频域点数，为了保证恢复的质量，一般取k≻N，m表示迭代次数。同样考虑子孔径数目J和距离向采样点数K，则整个恢复处理的总运算复杂度为J·K·m·O（2k N2+ k N+N3）。通过比较两种算法的运算复杂度，可以看出本文所述算法的运算效率明显优于GAPES算法，而运算时间则远远小于GAPES算法的运算时间。

6　结　论

本文提出了一种利用压缩感知恢复条带模式SAR缺失数据的方法。首先将条带数据分块成子孔径数据，通过CS恢复无缺失的子孔径数据并进行拼接，得到条带全孔径数据，使条带缺失数据恢复的计算量满足目前的硬件要求。通过稀疏EMMLE算法对子孔径进行自聚焦，保证了子孔径重构图像的稀疏度要求。利用CS对缺失相位误差信号进行恢复，保证了子孔径拼接的正确性。通过传统条带模式成像算法成像并自聚焦可以校正距离徙动，并补偿相位误差，保证了图像的成像质量。实测数据处理结果表明了本文方法的正确性，解决了缺失数据的重影问题。本文所述方法的图像熵值明显低于其他成像结果，证明本文所述方法提高了缺失数据的成像质量，说明本文提出的方法是可行且有效的。

［1］Larsson E G，Liu GQ，Stoica P，et al.High-resolution SAR imaging with angular diversity［J］.IEEE Trans.on Aerospace and Electronic Systems，2001，37（4）：1359-1372.

［2］Glentis G O，Zhao K X，Jakobsson A，et al.Non-parametric high-resolution SAR imaging［J］.IEEE Trans.on Signal Processing，2013，61（7）：1614-1624.

［3］Du X Y，Duan C W，Hu W D.Sparse representation based autofocusing technique for ISAR images［J］.IEEE Trans.on Geoscience and Remote Sensing，2013，51（3）：1826-1835.

［4］Bai X R，Zhou F，Xing MD，et al，High-resolution radar imaging of air targets from sparse azimuth data［J］.IEEE Trans.on Aerospace and Electronic Systems，2012，48（2）：1643-1654.

［5］Alan V O.Signals and system［M］.2nd ed.Beijing：Publishing House of Elecronincs Industry，2010：263-274.

［6］Gupta I J，High resolution radar imaging using 2D linear prediction［J］.IEEE Trans.on Antennas Propagation，1994，42（1）：31-37.

［7］Gupta I J，Beals M J，Moghaddar A，et al.Data extrapolation for high-resolution radar imaging［J］.IEEE Trans.on Antennas and Propagation，1994，42（11）：1540-1545.

［8］Erer I.A new data extrapolation algorithm for high resolution ISAR imaging［J］.International Journal of Electronics and Communications，2006（60）：316-319.

［9］Stoica P，Larsson E G，Li J.Adaptive filterbank approach to restoration and spectral analysis of gapped data［J］.The Astronommical Journal，2000（120）：2163-2173.

［10］Larsson E G，Stoica P，Li J.Amplitude spectrum estimation for two-dimensional gapped data［J］.IEEE Trans.on Signal Processing，2002，50（6）：1343-1354.

［11］Stoica P，Li J，Ling J.Missing data revovery via a nonparametric iterative adaptive approach［J］.IEEE Signal ProcessingLetters，2009，16（4）：241-244.

［12］Baraniuk R G.Compressive sensing［J］.IEEE Signal Processing Magazine，2007，118：118-124.

［13］Wang C Y，Xu J.Improved optimization algorithm for measurement matrix in compressed sensing［J］，Systems Engineering and Electronics，2015，37（4）：752-756.（王彩云，徐静.改进的压缩感知测量矩阵优化方法［J］.系统工程与电子技术，2015，37（4）：752-756.）

［14］Dong X，Zhang Y H.A novel compressive sensing algorithm for SAR imaging［J］.IEEE Journal of Selected Topics in Applied Earth Obserυations and Remote Sensing，2014，7（2）：708-720.

［15］Fang J，Xu Z B，Zhang B C，et al，Fast compressed sensing SAR imaging based on approximated observation［J］.IEEE Journal of Selected Topics in Applied Earth Obserυations and Remote Sensing，2014，7（1）：352-363.

［16］Liu J H，Xu S K，Gao X Z，et al.Novel imaging methods of stepped frequency radar based on compressed sensing［J］.Journal of System Engineering and Electronics，2012，23（1）：47-56.

［17］Yang J G，Thompson J，Huang X T，et al.Random-frequency SAR imaging based on compressed sensing［J］.IEEE Trans.on Geoscience Remote Sensing，2013，51（2）：983-994.

［18］Yang J G，Huang X T，Jin T，et al.Synthetic aperture radar imaging using stepped frequency waveform［J］.IEEE Trans. on Geoscience Remote Sensing，2012，50（5）：2026-2036.

［19］Potter L C.Ertin E，Parker J T，et al.Sparsity and compressed sensing in radar imaging［J］.Proceedings of the IEEE，2010，98（6）：1006-1020.

［20］Alonso M T，Lopez-Dekker P，Mallorqui JJ.A novel strategy for radar imaging based on compressive sensing［J］.IEEE Trans.on Geoscience and Remote Sensing，2010，48（12）：4285-4295.

［21］Patel VM，Easley G R，Healy DM，et al，Compressed synthetic aperture Radar［J］.IEEE Journal of Selected Topics in Signal Processing，2010，4（2）：244-254.

［22］Yang J G，John T，Huang X T，et al，Segmented reconstruction for compressed sensing SAR imaging［J］.IEEE Trans.on Geoscience and Remote Sensing，2013，51（7）：4214-4225.

［23］Wang WW，Liao G S，Zhang L，et al，An imaging method based on compressed sensing for sparse aperture of SAR［J］. Acta Electronica Sinica，2012，40（12）：2487-2494.（王伟伟，廖桂生，张磊，等.一种基于压缩感知的稀疏孔径SAR成像方法［J］.电子学报，2015，40（12）：2487-2494.）

［24］Cumming I G，Wong F H.Digital processing of synthetic aperture radar data：algorithm and implementation［M］.Beijing：Publishing House of Electronics Industry，2012：192-215.（Cumming I G，Wong FH.合成孔径雷达成像—算法与实现［M］.北京：电子工业出版社，2012：192-215.

［25］Jiang R，Zhu D Y，Zhu Z D.A novel approach to strip-map SAR autofucos［J］.Acta Aeronautica et Astronautica Sinica，2012，40（6）：1251-1256.（蒋锐，朱岱寅，朱兆达.一种用于条带模式SAR成像的自聚焦算法［J］.航空学报，2010，12（31）：2385-2392.）

［26］Sun J P，HongW，Liu C K，et al.Spotlight processing of stripmap SAR data［J］.Acta Aeronautica et Astronautica Sinica，2001，22（S1）：80-83.（孙进平，洪文，柳成堪，等.条带模式合成孔径雷达回波数据的聚束成像算法处理［J］.航空学报，2001，22（S1）：80-83.）

［27］Garrana W G，Goodman R E，Majewski R M.Spotlight synthetic aperture radar signal processing algorithms［M］.Boston：Artech House，1995：81-107.

［28］Aushermen D A，Kozma A，Walker J L，et al，Developments in radar imaging［J］.IEEE Trans.on Aerospace and Electronic Systems，1984，20（4）：363-400.

［29］Tropp J A，Gilbert A C.Signal recovery from randommeasurements via orthogonal matching pursuit［J］.IEEE Trans.on Information Theory，2007，53（12）：4655-4666.

［30］Potter L C，Ertin E，Parker J T，et al.Sparsity and compressed sensing in radar imaging［J］.Proceedingsof the IEEE，2010，98（6）：1006-1020.

［31］Baraniuk R，Steeghs P.Compressive radar imaging［J］.Proceedings of the IEEE Radar Conference，2007，17（20）：128-133.

［32］Wahl D E，Eichel H P，Ghiglia D C，et al.Phase gradient autofocus-a robust tool for high resolution SAR phase correction［J］. IEEE Trans.on Aerospace and Electronic Systems，1994，30（3）：827-835.

［33］Charles V J，Daniel EW.Eigenvector method for maximumlikelihood estimation of phase errors in synthetic aperture Radar imagery［J］.Journal of the Optical Society of America，1993，10（12）：2539-2546.

［34］Yu X，Zhu D Y.A motion compensation algorithm for 2dimensional compressed ISAR imaging［J］，Acta Electronica Sinica，2012，40（9）：1783-1789.（俞翔，朱岱寅.一种ISAR二维压缩感知成像的运动补偿方法［J］.电子学报，2012，40（9）：1783 1789.）

［35］Glentis G，Gilbert A.Efficient implementation of iterative adaptive approach spectral estimation techniques［J］.IEEE Trans.on Signal Processing，2011，52（9）：4154-4167.

Recovery and imaging method for missing data of the strip-map SAR based on compressive sensing

DUAN Hua-jun，ZHU Dai-yin，LI Yong，WU Di
（Key Laboratory of Radar Imaging&Microwaυe Photonics of Ministry of Education，College of Electronic& Information Engineering，Nanjing Uniυersity of Aeronautics&Astronautics，Nanjing 210016，China）

A recovery and imaging method for missing data of the strip-map mode synthetic aperture radar（SAR）based on compressive sensing（CS）is introduced.The strip-map data is segmented into several sub-apertures，which results in reducing the recovery time significantly.The sub-aperture missing data can be restored by CSand be stitched to the strip-map data.The basis matrix and the measurement matrix for CSare proposed. The sub-aperture data are autofocused by the eigenvector method for maximum-likelihood estimation to meet the sparse requirement of the reconstructed image and the intact phase error data is restored by CSin order to stitch the sub-aperture.A high quality image of the restored data can be obtained by the conventional imaging method and autofocus which corrects the range migration.

synthetic aperture radar（SAR）；compressive sensing（CS）；eigenvector method for maximumlikelihood estimation（EMMLE）；recovery data

TN 958

A

10.3969/j.issn.1001-506X.2016.05.09

1001-506X（2016）05-1025-07

2015-07-27；

2015-10-21；网络优先出版日期：2016-01-07。

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160107.1127.006.html

国家自然科学基金（61301212）；航空科学基金（20132052030，20142052020）；中央高校基本科研业务费专项资金（NP2015504）；中国博士后科学基金（2012M511750）；国防基础科研计划（B2520110008）；江苏省研究生培养创新工程（SJLX_0131）；江苏高校优势学科建设工程资助课题

段化军（1976-），男，工程师，博士研究生，主要研究方向为雷达信号处理与稀疏SAR成像。

E-mail：dhj5816@sina.com

朱岱寅（1974-），男，教授，博士，主要研究方向为雷达信号处理及雷达成像技术研究。

E-mail：zhudy@nuaa.edu.cn.

李勇（1977-），男，副教授，博士，主要研究方向为雷达信号处理。

E-mail：limack@nuaa.edu.cn

吴迪（1982-），男，副教授，博士，主要研究方向为机载雷达地面动目标检测。

E-mail：wudi82@nuaa.edu.cn