基于矩阵束的多波段雷达信号高精度融合成像算法

邹永强，高勋章，黎　湘

（国防科学技术大学电子科学与工程学院，湖南　长沙 410073）

基于矩阵束的多波段雷达信号高精度融合成像算法

邹永强，高勋章，黎湘

（国防科学技术大学电子科学与工程学院，湖南长沙 410073）

多波段信号融合技术在信号层将多个不同子带融合成一个大带宽信号，因而能够有效提高雷达图像距离分辨率。目前，基于全极点模型的融合技术主要采用root-MUSIC（multiple signal classification）及其改进算法实现极点的估计，在较弱的噪声条件下这种方法得到了不错的融合效果。然而在低信噪比条件下root-M USIC算法容易受到噪声干扰而难以实现正确极点获取，进而极大影响到最终信号融合效果。为减小噪声影响，提出用矩阵束算法实现多波段信号极点估计，在此基础上通过不同子带对应极点间的相位关系估计出相干参数，同时对融合结果以信号差的2范数最小为准则进行迭代，以减小融合信号的误差。最后采用加权寻优的方式进一步提高了信号的融合精度。仿真实验结果表明，提出的方法有效提高了低信噪比条件下的多波段信号融合效果。

多波段信号；全极点模型；矩阵束；迭代算法；加权寻优

网址：www.sys-ele.com

0　引　言

多波段雷达融合成像技术是现有条件下获得高分辨逆合成孔径雷达（inverse synthetic aperture radar，ISAR）像的有效途径［1-4］。在硬件上它仅需对几部工作在不同频段的宽带雷达加装必须的同步设备，这大大降低了获取大带宽雷达信号的难度，但也给目前的雷达成像算法带来一些挑战［5-9］，其中两个重要的问题是多子带信号相参补偿［10-11］和宽带信号衰减指数和模型的高精度参数估计［12］。

之所以要对不同子带信号进行相参补偿是由于参与带宽合成的多子带目标回波数据来自不同的雷达，即使采用高精度的时空频同步技术［13-14］，硬件差异以及设备工作过程中的不稳定性依然会使信号间相参性变差，而雷达成像对信号相参性要求较为苛刻，如果不补偿，在各子带相参性差别不大的情况下会使融合雷达像散焦和模糊，严重情况下将不能成像。很多学者已经对这个问题开展研究，最早也是最详细论述这一问题的是林肯实验室的Cuomo［12］。他通过对多波段雷达的分析，总结得出各种因素导致的不相参最终表现为在信号上引入了一个线性相移和一个固定相移。基于此结论他提出用root-MUSIC（multiple signalclassification）和最小二乘法建立每个波段的全极点模型，而后依据该模型进行数据外推，以其中一个波段的数据为基准通过最优化的方法得到线性相移和固定相移的估计，最后进行校正。信号的高维度特点以及要同时对多个参数进行优化导致这种方法的计算量较大，同时数据外推也会带来一定的误差。文献［15］提出利用目标一维像相关直接求取线性相移，并结合一个代价函数求取固定相移的方法，该方法效率较高，但受限于信号采样数，其参数估计往往达不到理想的精度。文献［10-11］直接根据不同子带对应极点的表达式推导出相干参数的计算公式，该方法不需要进行外推，计算也较为简单，但推导过程中忽略了不同子带之间的频带间隔对相位的影响，同时使用root-MUSIC算法估计极点也会影响到该算法在低信噪比下的性能。

对于衰减指数和模型参数的估计，现在大多数研究将其转化为一个全极点模型，采用模型定阶方法确定极点个数k，用root-MUSIC和最小二乘法得到极点估计值，其中极点选取的是离单位圆最近的k个极点。由衰减指数和模型与全极点模型的关系可知，这些极点由于引入了衰减项导致它们会不同程度地偏离单位圆，因此root-M USIC的这种极点选择方法本身并不是稳健的。在噪声影响非常小的情况下能够达到较为理想的效果，但是当噪声较强时，一些本来偏离单位圆较远的干扰极点可能会比真正的极点更靠近单位圆，从而导致极点选取错误。这个错误对信号融合后续所有步骤及最终结果都会产生极大影响，因此必须努力提高较强噪声环境下极点估计的准确性。

为解决上述几个问题，本文首先提出用矩阵束来估计极点，该方法在较低信噪比下依然能实现极点的有效估计。然后从理论上分析了相参失配信号的极点差异，既而提出不依赖于数据外推和信号采样数的相参补偿方法。之后为了提高融合信号的精度，本文先提出了一个以信号差的2范数最小为准则的多波段信号迭代融合流程，之后又提出基于各子带和融合信号模型参数的加权寻优方法。最后用仿真数据试验验证了上述方法的有效性。

1　多波段雷达信号相参补偿

基于前面的分析，本文针对文献［10］方法的不足进行改进，有效提高较强噪声条件下相干参数的估计精度。设两部邻近配置（同视角观测）的雷达独立工作，其起始频率分别为f1，f2，频率步进数分别为N1，N2，二者跳频间隔均为Δf，且f2=f1+ΔB，ΔB＞Δf·N1，ΔB 为两部雷达起始频率间隔。对于由M个散射点构成的静止目标，两部雷达的基带回波分别为

式（1）和式（2）分别是s1和s2的几何绕射理论（geometrical theory of diffraction，GTD）模型表示，其中模型参数｛Am，rm，αm｝Mm=1表征了这M个散射中心的特性，Am是散射中心的幅度系数，rm为散射中心相对于参考点的距离，αm是0.5的整数倍，表征散射中心的几何类型。fk=f1+k·Δf，fk′= f2+k′·Δf，c为电磁波在空气中的传播速度，这里近似为光速。η和θ分别为导致s1和s2不相参的固定相移和线性相移，即要估计的相干参数。

式（1）和式（2）较精确地描述了信号基带回波，但由于频率依赖项的存在导致其计算困难，本文采用与文献［16］类似的方法将幂函数用指数函数近似，这样以上两式就转换为式（3）、式（4）的衰减指数和模型。为便于求解还可进一步等效为全极点模型，即

式中，用βfm代替了fαm项［16］；pm，qm分别为s1，s2的极点；bm，dm分别为s1，s2的极点对应的幅度系数。

全极点模型本质上是谐波的叠加，可用谐波分解算法求解，其中矩阵束算法是性能较优的方法。它由文献［17］最早提出，是经典旋转不变技术（estimation of signal parameters via rotational invariance technique，ESPRIT）的一种变形，其思路是利用指数和信号的性质，通过求解矩阵束的广义特征值一次性地估计出指数和模型的极点［18］。文献［16，18-19］对MUSIC、root-MUSIC、ESPRIT、矩阵束等几种方法进行对比，从而可知矩阵束方法相对于其他几种方法在低信噪比下有更好的性能。为此本文将用矩阵束方法对式（3）和式（4）的参数进行估计。

以信号s1为例，首先要构造如下Hankel矩阵，即N1-。模型阶数的估计值由最小描述长度法（minimum description length，MDL）或者Akaike信息量准则法（Akaike information criterion，AIC）确定。然后对Hankel矩阵X0和X1进行奇异值分解，得

式中，Δ、Σ分别是由X0，X1的个主奇异值构成的对角矩阵，它们以及与其对应的U0、V0、U1、V1包含信号信息和少量噪声信息；ΔM0-、ΣM0-分别是X0，X1的M0-个非主奇异值构成的对角矩阵，它们以及与其对应的U′0、V′0、U′1、V′1只包含噪声信息。为减少噪声，令

求出矩阵束X1s-λX0s的个广义特征值即可得到极点的估计。

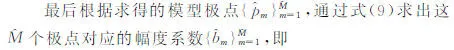
Vandermonde矩阵。

通过上述矩阵束方法求得的s1、s2的极点分别为

由式（10）可知，s1和s2同阶极点的相角只相差一个线性相位θ。因此，θ可由式（11）估计得到

相应的，用矩阵束方法得到的同阶极点的幅度估计值为

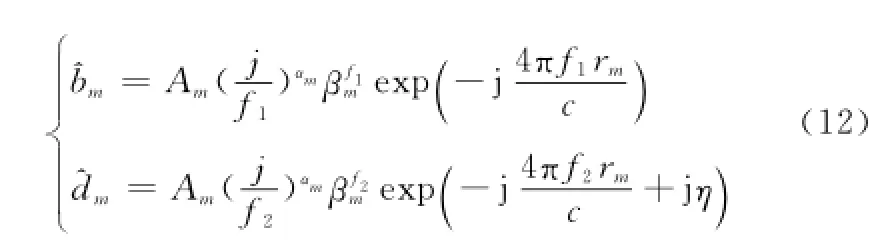
与估计线性相位的情况不同，这两个信号同阶极点的幅度所对应的相角不仅仅相差一个固定相移η，它还与频率、相对距离rm以及散射中心类型参数αm有关，即

上面的参数估计中没有对αm进行估计，所以这里无法知道的数值，但是仔细分析后可知

又f2=f1+ΔB，所以由式（15）可以得到固定相移的估计，即

本方法从两个方面保证了较高的相干参数估计精度：一是采用抗噪性能好的矩阵束方法估计全极点模型参数，这使得参数的估计受到噪声的干扰减小，估计结果也更稳健。二是本方法不需要对数据进行外推，从而减少了数据外推可能带来的误差。另外由于没有用到多个参数的最优化方法，本算法的计算量也较小。

2　多波段雷达信号融合成像

文献［10-11］用缺失数据幅度相位估计（gapped-data amplitude and phase estimation，GAPES）算法填充缺失数据，然后对全频段数据用root-MUSIC算法估计模型参数来实现数据的预测，仿真实验得到了较为清晰的融合图像。但是该算法没有将融合结果反馈到参数估计中，而且其中的GAPES拟合数据本身存在较大误差，这些都会影响融合效果。为此本文在上一节算法基础上提出基于矩阵束的多波段信号高精度融合算法，该算法用矩阵束算法估计全频带的全极点模型参数（本文中的全频段是指子带与通过融合方法得到的频段的总和），继而实现空缺频带的数据预测。同时本算法对数据预测结果进行评判，根据结果进行迭代，然后又引入基于子带和融合信号参数的加权寻优，进一步提高信号融合精度。以频带间隔ΔB的两个子带信号s1、s2（二者数据长度分别为N1、N2，全频段数据总长度为N）融合为例，该算法详细步骤如下：

步骤1用上一小节的相参补偿算法对两个子带进行相参补偿，得到相参的子带信号s1和，为方便表述，令s2=，即用s2代表已经和s1相参的子带信号。

步骤2基于相参子带数据估计全频段全极点模型参数。

设全频段全极点模型为

依然用矩阵束方法对式（18）进行估计，但与前面不同的是信号由频带上相差ΔB的两段信号组成，为了能够应用矩阵束算法，令

之后的步骤可参照上一节进行。

步骤3得到各阶极点及其幅度的估计后可按照式（21）得到全频段数据的估计。

为减小估计误差应尽量使用原始的测量数据，那么全频段的融合信号为

步骤4算法中引入迭代以提高信号融合质量。

各子带的估计信号与原始测量信号的差能反映出全极点模型与测量数据的近似程度，但这个差是复向量的形式，为便于比较本文取其2范数作为衡量融合效果的标准。

步骤5加权寻优。

由于全频段融合数据的极点和幅度仅由不重叠的两段数据预测而来，缺少中间空缺频段的数据，所以就会产生因信息不全导致的误差。这个误差通过上面的迭代方法还不能完全消除，这里我们通过加权寻优的方式来进一步减小这个误差。

设加权后的全频段极点的幅度和相角分别为

式中，r为相似系数，其定义为

那么，L=｛λ（k）|k∈K｝就是能够提高融合精度的λ值的集合。由于L中的值可能不止一个，而且rk1，rk2往往不能同时达到最大值，所以为了均衡起见，本文选择λ（kopt）作为最佳的加权值，其中kopt由式得到。

将λ（kopt）代入到式（25）和式（26）中，就可以得到最佳的极点和幅度估计，继而获得最佳全频段融合信号。

总结以上步骤并考虑到实际信号的情况，本文多频段信号融合算法主要流程如图1所示。在相参补偿之前还加入了一些步骤主要是因为目前大多数宽带雷达发射的都是线性调频信号，目标回波要经过dechirp处理才得到类似式（1）的基带信号。同时，为了满足融合成像的需要，还必须对信号进行平动补偿和初相校正。

图1　基于矩阵束的多频段信号融合流程

对最后得到的全频段融合信号进行脉冲压缩就可以得到全频段的一维像，二维像只需在一维像的基础上进行横向压缩即可。

3　仿真实验与分析

为检验算法性能，首先用本文提出方法（简称算法1）、文献［12］的方法（简称算法2）和文献［10］的方法（简称算法3）对基于GTD模型的仿真数据进行相参补偿和信号融合实验。之后进一步测试算法，在弹头模型的CST2012电磁计算数据中加入不同信噪比高斯白噪声，用上述3种算法对含噪信号融合成像。

3.1多波段雷达信号相参补偿及融合实验

本实验中雷达的起始频率为f0=8 GHz，跳频间隔Δf= 10 M Hz，频率步进数N=300，总的带宽B=3 GHz，则理论距离分辨率为0.05 m。目标由3个离散的散射中心组成，参考距离Rref=15 km，各点的其他参数如表1所示。

表1　各散射点参数设置

那么目标的含噪回波为

式中，k∈N+，fk=f0+kΔf，e（k）是零均值高斯白噪声。令

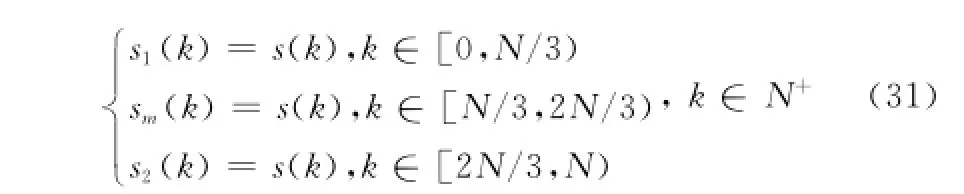
在s2中加入固定相移η=π/8和线性相移θ=π/9以模拟信号间不相参，因此得到s′2（k）=s2（k）exp（jη+j kθ）。在信噪比为1～20 dB条件下，分别用上述3种算法估计固定相移和线性相移。图2给出了经100次蒙特卡罗仿真后，非相参量估计值的均方根误差（root mean square error，RMSE）随信噪比的变化曲线。从中可以看出3种算法的RMSE都随着信噪比的降低而不同程度的变大，其中本文方法的估计精度最高，而且误差的波动相对于其他两种算法比较平缓，这一方面是由于本文算法没有带宽外推从而减少了这一因素可能带来的误差，另一方面是矩阵束算法本身具有较好的抗噪能力。可见本文方法确实提高了非相干参数的估计精度。

图2　非相干参数估计误差分析

在信噪比为15 d B的条件下，用相参补偿后的s1、s2作为低、高频带，用3种算法来估计sm，进而实现频带融合。图3是3种算法得到的sm估计值与原始信号的对比，其中图3（a）、图3（d）分别是算法1的初始估计结果和迭代后的最终结果。从图3中可知，这3种算法得到的缺失频带信号与原始信号大部分频段都可以拟合，但是有些频段拟合的效果较差。总体来看，在信噪比为15 dB的条件下算法1的初始估计结果优于其他算法，但与原始信号相比仍有较大误差，而通过迭代和加权寻优后估计误差明显减小。这说明算法1采用的矩阵束算法参数估计精度较高，同时迭代和加权寻优的引入确实提高了数据的估计精度。

将算法1最终估计到的空缺频带信号按式（31）的形式与s1、s2组成全频带融合信号，它与原始测量数据s的波型及一维像如图4所示。

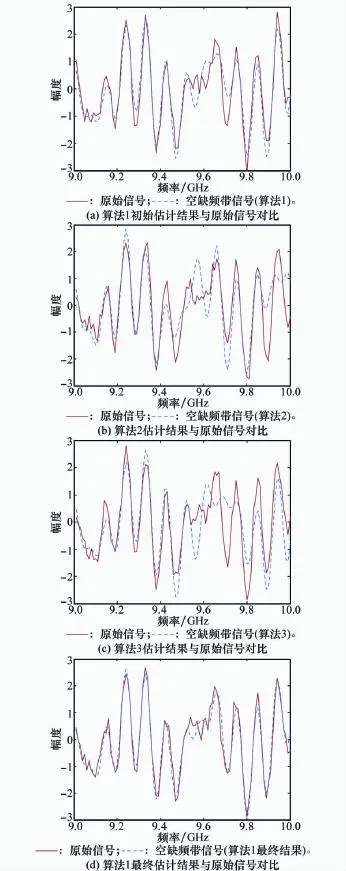
图3　空缺频带估计结果

可见融合信号与原始信号实现了较好的拟合，而且由于带宽的增加，全频带融合信号的一维像将3个点全部分开（上面的各子带信号由于带宽只有1 GHz，导致了第1、第2散射中心无法分开），达到了提高分辨率的预期效果。

3.2多频段融合的二维ISAR像

图4　本文算法最终融合效果

本文用电磁计算软件CST2012建模并计算模型不同方位角下的扫频数据。该模型是由一个半球和两个圆台组成的简易弹头（见图5（a）），其各部分的参数如表2所示。实验中弹头的方位角规定如下，弹头顶端正对雷达时其方位角为0°，逆时针旋转为正，顺时针旋转为负。计算开始前参数设置为：方位角0°～10°，角度间隔0.1°，频率10～14 GHz，频率间隔20 M Hz。记所得到的信号矩阵为X，则其任意元素xi，j的角标应满足i∈［1，201］，j∈［1，101］。用距离-多普勒算法成像即可得到如图5（b）所示结果。

表2　弹头模型参数

为模拟两部雷达的回波X1和X2，本文对X的数据进行分配

图5　弹头模型及其二维ISAR像

由式（32）可知，模拟的两部雷达频带范围分别为10～11 GHz和13～14 GHz。它们所成的二维ISAR像如图6所示。由于带宽较窄，图6的两幅图像的距离向分辨率均不高，确定强散射点的精确位置比较困难。

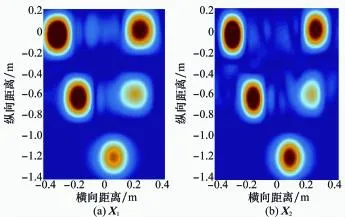
图6　低、高频段二维ISAR像

为检验算法整体性能，在X2中加入固定相移η=π/8和线性相移θ=π/9，然后在X中分别加入信噪比为15 d B和10 dB的高斯白噪声，用前面的3种算法进行多波段融合处理，最后用距离多普勒（range-Doppler，R-D）算法成像，所得结果如图7和图8所示。

图7　信噪比为15 dB时融合结果对比

信噪比为15 dB条件下，与图6相比图7（b）～图7（d）中的融合图像分辨率明显提高，大多数散射点的位置能够较为精确的给出。与图7（a）相比，各融合图像散射点出现了不同程度的散焦，导致一些散射点模糊。其中图7（d）有一个散射点十分模糊，已经不能分辨。图7（c）的各个散射点虽然都可以分辨，可是散射点周围有较强的虚影。图7（b）与图7（c）、图7（d）相比散射点能量相对集中，它与图7（a）最为接近。

在信噪比为10 dB的条件下，含噪原始测量数据成像依然较为清晰，但融合图像受噪声影响较大。图8（c）～图8（d）的分辨率相对于图6有一定提高，然而它们的虚假散射点数量多且能量较强，难以区分真假散射点。图8（b）也存在类似的情况，但其散焦不是很严重，各个散射点较容易分辨。

为了更好的对比试验结果，本文计算出图7、图8中每幅ISAR像的图像熵［20］，其结果如表3所示。

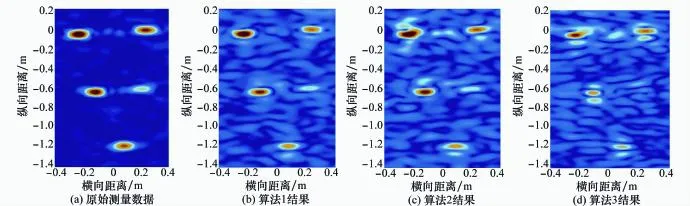
图8　信噪比为10 dB时融合结果对比

表3　ISAR的图像熵

以上实验结果可知，在信噪比为15 dB时，3种融合算法差别不大，但因矩阵束抗噪性能优于root-MUSIC以及迭代和加权寻优过程的引入导致本文方法融合效果较好。在信噪比降低到10 d B时，虽然各融合图像质量都有较明显下降，但是算法1得到的图像明显好于其他2幅，本文算法的优势进一步体现。

4　结　论

本文在估计全极点模型参数时用矩阵束算法代替了通常使用的root-MUSIC算法，保证了较低信噪比条件下参数的估计精度。同时在融合过程中引入基于信号差2范数的迭代流程和基于各子带及融合信号参数的加权寻优过程，进一步提高了融合信号的质量。与其他融合算法的对比实验表明，本文提出的方法能较好保证低信噪比下的融合信号精度。但是从实验结果中也可以看出噪声对融合结果影响很大，虽然本文采用噪声环境下性能优异的参数估计算法，但是依然无法彻底消除噪声的不利影响。如果能在融合流程前提高信号的信噪比，相信会得到更好的融合效果。

［1］Chen L，Chen J.High resolution radar imaging using bandwidth extrapolation［C］//Proc.of the 3rd International Congress on Image and Signal Processing（CISP），2010：3591-3595.

［2］Sacchi M D，Ulrych T J，Walker CJ.Interpolation and extrapolation using a high-resolution discrete Fourier transform［J］.IEEE Trans. on Signal Processing，1998，46（1）：31-38.

［3］NaishadhamK，Piou J E.State-space spectral estimation of characteristic electromagnetic responses inwideband data［J］. IEEE Trans.on Antennas and Wireless Propagation Letters，2005，4：406-409.

［4］Wang Q，Wu R B，Xing M D，et al.A new algorithm for sparse aperture interpolation［J］.IEEE Trans.on Geoscience and Remote Sensing Letters，2007，4（3）：480-484.

［5］He F Y，Xu X J.High-resolution imaging based on coherent processing for distributed multi-band radar data［J］.Progress in Electromagnetics Research，2013，141（4）：383-401.

［6］Xu X J，Li J.Ultrawide-band radar imagery from multiple incoherent frequency subband measurements［J］.Journal of Systems Engineering and Electronics，2011，22（3）：398-404.

［7］Van Dorp P，Ebeling R，Huizing AG.High resolution radar imaging using coherent multiband processing techniques［C］//Proc.of the IEEE Conference on Radar，2010：981-986.

［8］Tian J H，Sun J P，Wang G H，et al.Multiband radar signal coherent fusion processing with IAA and ap FFT［J］.IEEE Trans. on Signal Processing Letters，2013，20（5）：463-466.

［9］Ba X R，Zhou F，Wang Q，et al.Sparse subband imaging of space targets in high-speed motion［J］.IEEE Trans.on Geoscience and Remote Sensing，2013，51（7）：4144-4154.

［10］Tian B，Chen Z P，Xu S Y.Sparse subband fusion imaging based on parameter estimation of geometrical theory of diffraction model［J］. IET Radar，Sonar and Naυigation，2014，8（4）：318-326.

［11］Tian B，Liu Y，Xu S Y，et al.Multi-band fusion imaging based on high precision parameter estimation of geometrical Theory of diffraction model［J］.Journal of Electronics&Information Technology，2013，35（7）：1532-1539.（田彪，刘洋，徐世友，等.基于几何绕射理论模型高精度参数估计的多频带合成成像［J］.电子与信息学报，2013，35（7）：1532-1539.）

［12］Cuomo K M，Piou J E，Mayhan J T.Ultra-wideband coherent processing［J］.IEEE Trans.on Antennas and Propagation，1999，47（6）：1094-1107.

［13］Yang Y，Blum R S.Phase synchronization for coherent MIMO radar algorithms and their analysis［J］.IEEE Trans.on Signal Processing，2011，59（11）：5538-5557.

［14］Sun P L，Tang J，He Q，et al.Cramer-Rao bound of parameters estimation and coherence［J］.IET Radar，Sonar and Naυigation，2013，7（5）：553-567.

［15］Fu R W，Zhang C，Li X，et al.Research on multi band radar fusion of one dimensional super resolution imaging technology［J］. Progress in Natural Science，2006，16（10）：1310-1316.（付耀文，张琛，黎湘，等.多波段雷达融合一维超分辨成像技术研究［J］.自然科学进展，2006，16（10）：1310-1316.）

［16］Gao X Z.High resolution radar imaging based on higher-order statistic［D］.Changsha：National University of Defense Technology，2004.（高勋章.基于高阶统计量的雷达目标高分辨成像研究［D］.长沙：国防科技技术大学，2004.）

［17］Hua Yin-bo，Sarkar T K.Matrix pencil method for estimating parameters of exponentially damped/undamped sinusoids in noise［J］.IEEE Trans.on Acoustics，Speech and Signal Processing，1990，38（5）：814-824.

［18］Sarkar T K，Pereira O.Using the matrix pencil method to estimate the parameters of a sum of complex exponentials［J］. IEEE Antennas and Propagation Magazine，1995，37（1）：48-55.

［19］Roy R，Paulraj A，Kailath T.Comparative performance of ESPRIT andMUSIC for direction-of-arrival estimation［C］//Proc.of the IEEE International Conference on Acoustics，Speech，and Signal Processing（ICASSP），1987（12）：2344-2347.

［20］Gao Q，Xue L，Wang Z N，et al.Imaging processing method for linear array ISAR based on image entropy［J］.Computer Engineering and Applications，2012，48（32）：125-128.（高强，薛乐，王振楠，等.基于图像熵的线性阵列ISAR成像处理方法［J］.计算机工程与应用，2012，48（32）：125-128.）

Multiband radar signal high precision fusion imaging method based on matrix pencil algorithm

ZOU Yong-qiang，GAO Xun-zhang，LI Xiang
（School of Electronics Science and Technology，National Uniυersity of Defense Technology，Changsha 410073，China）

The multiband signal fusion technique can improve the range resolution of the radar image efficiently by fusing several subbands to a great wide band signal in the signal level.At present，the all-pole model based fusion algorithms mainly apply the root-multiple signal classification（MUSIC）and its modified method to estimate the signal poles，and good results are obtained in weak noise conditions.However，the root-MUSIC method which is fragile in noise could not easily get proper poles in low signal-to-noise ratio（SNR）.In order to eliminate the influence of noise，a matrix pencil algorithm based method is proposed to estimate the multiband signal poles.And then the coherent parameters of multiband signals are calculated through the relation of corresponding poles.At the same time，an iterative algorithm which aims to minimize the 2-norm of signal difference is introduced to reduce signal fusion error.Apart from that a weighted optimization method is also presented to improve the fusion precision.Applications to simulate dada verify that the proposed method could get better fusion results at low SNR.

multiband signal；all-pole model；matrix pencil；iterative algorithm；weighted optimization

TN 95

A

10.3969/j.issn.1001-506X.2016.05.08

1001-506X（2016）05-1017-08

2015-04-22；

2015-09-28；网络优先出版日期：2016-02-04。

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160204.1506.002.html

国家杰出青年科学基金资助项目（61025006）资助课题

邹永强（1986-），男，博士研究生，主要研究方向为雷达成像、数据融合、雷达自动目标识别。

E-mail：zouyongqiangnudt@yeah.net

高勋章（1972-），男，教授，博士，主要研究方向为信息融合、自动目标识别、雷达信号处理。

E-mail：gaoxunzhang@nudt.edu.cn

黎湘（1967-），男，教授，博士，主要研究方向为雷达系统与信号处理、非线性信号处理、雷达自动目标识别。

E-mail：xiangli@nudt.edu.cn