例析指数函数有关问题

安徽省太和中学　阮飞

例析指数函数有关问题

安徽省太和中学阮飞

在学习了函数的概念和函数的一般性质的基础上，我们具体研究的第一个重要函数就是指数函数。在学习指数函数过程中，我们利用了观察、分析、抽象、概括等方法，体会了从特殊到一般、数形结合等思想。我们要深入理解，不断提高我们的数学素养。

一、指数运算

包含根式概念、分数指数幂的运算等，重点理解指数幂的运算性质。注意以下两点：

2.注意将根式化为分数指数、负指数化为正指数的运算顺序，会用运算律求值和化简。

例1已知f（x）=3x，

求证：（1）f（x+y）=f（x）·f（y）。

证明（1）因为f（x）=3x，所以f（x）

又因为f（x+y）=3x+y，所以f（x+y）=f（x）·f（y）。

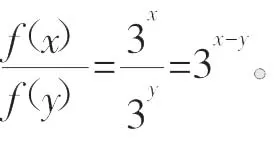
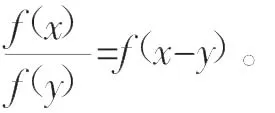
二、指数函数的概念

主要考查指数函数的概念、指数函数及其复合函数的定义域和值域等。

例2已知f（x）的定义域为（0，1），则f（3x）的定义域为_____。

解析因为f（x）的定义域为（0，1），所以0＜3x＜1，

所以x＜0，故应填（-∞，0）。

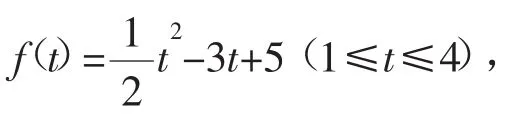
因为函数f（t）图像的对称轴方程为t=3，

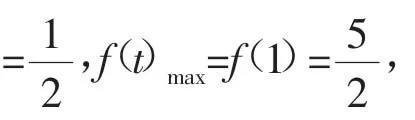
评注指数函数复合函数的模型主要有两种：

（1）y=f（ax），在用换元时要注意t=ax＞0这个条件。（2）y=af（x），注意0＜a＜1，a＞1和f（x）的定义域。

三、指数函数图像

1.指数函数图像特征

例4下列命题正确的有____。

（1）函数y=x0的图像是一条直线。

解析（1）x≠0，它表示的不是一条直线。

（3）画出函数y=x2，y=2x的图像，它们在y轴左边有一个交点，在y轴右边还有交点（2，4）和（4，16），A∩B的元素个数是3。

（4）由x2-2x＞0，得x＞2或x＜0。

综上所述，正确命题是（2）（3）（4）。

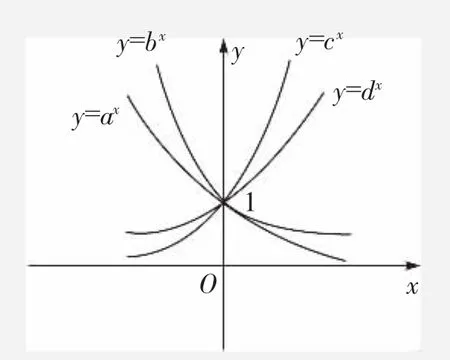
2.底数大小与指数函数图像间的关系

例5如图，则a、b、c、d与1的大小关系是（）。

A.a＜b＜1＜c＜d

B.b＜a＜1＜d＜c

C.a＜b＜1＜d＜c

D.1＜a＜b＜c＜d

解析方法一：结合四个函数的图像，由直线x=1与它们交点的纵坐标可知b＜a＜1＜d＜c。

方法二：在同一坐标系中，指数函数在第一象限的图像满足“底大图高”，结合图像知选B。

3.指数函数图像的应用

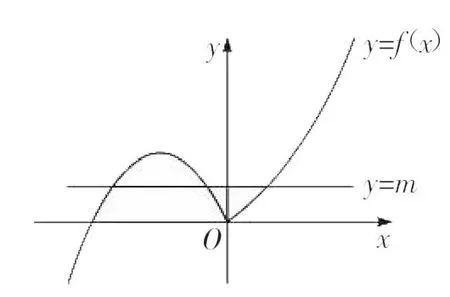
由题意知，方程f（x）-m=0即f（x）=m有三个实根，则y=f（x）与y=m有3个交点即可，画出图像，数形结合可得m的取值范围是（0，1）。

评注函数的零点即函数对应方程的根，一般可以转化为两个函数图像的交点个数问题。我们可以画出两个函数的图像，通过数形结合判断交点个数。

四、指数函数性质的应用

1.利用指数函数单调性比较幂的大小

因为y=2x是单调递增函数，

所以y1＞y3＞y2，故选B。

2.利用指数函数单调性求解不等式

例8不等式2x2-x＜4的解集为____。

解析原不等式可以变形为2x2-x＜22，则x2-x＜2，解得-1＜x＜2，所以原不等式的解集为（-1，2）。

解析当x<1时，x-1<0，ex-1<1，则ex-1≤2恒成立，故x<1符合题意；

综上可知，x的取值范围为（-∞，8］。评注分段函数问题需要分段考虑。

五、几种常见的含指数的函数

1.f（x）+f（a-x）=常数

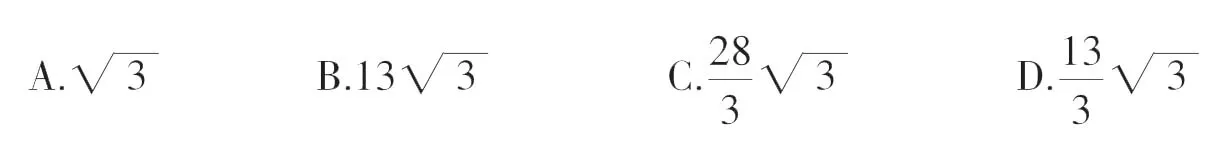
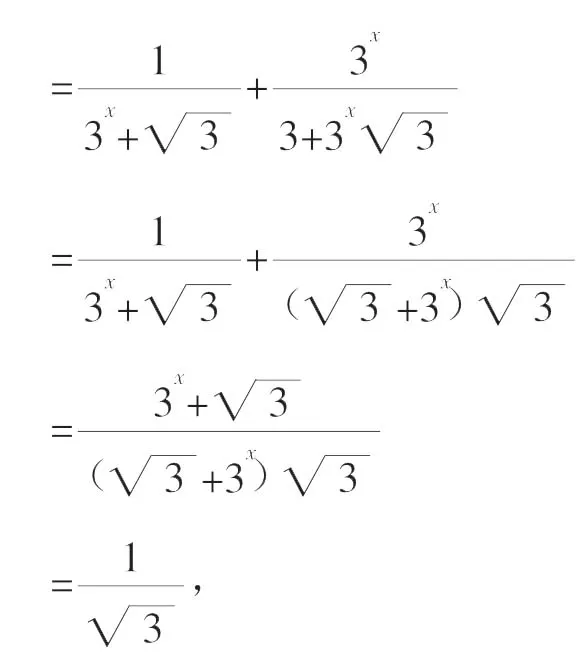
评注根据求和的整体形式特征，我们可以猜测：f（-12）+f（13）=f（-11）+f（12）=f（-10）+ f（11）=…=f（0）+f（1），而它们有共同的特点：-12+13=-11+12=…=0+1=1，经验证，f（x）+f（1-x）=常数，即可求得结果。

2.复合函数y=a|x-m|+b（a＞0，a≠1）的性质

例11若函数f（x）=2|x-a|（a∈R）满足f（1+x）=f（1-x），且f（x）在［m，+∞）单调递增，则实数m的

最小值等于____。

解析函数f（x）=2|x-a|（a∈R）的图像关于直线x=a对称，

又由f（1+x）=f（1-x）得函数f（x）的图像关于直线x=1对称，故a=1，

由复合函数单调性得f（x）在［1，+∞）递增，故m≥1，

所以实数m的最小值等于1。

评注函数y=a|x-m|+b（a＞0，a≠1）的图像关于直线x=m对称。利用函数的对称性确定a的值，利用复合函数的单调性（内外函数“同增异减”）确定函数单调区间，从而求得参数的取值范围。

求证：（1）［g（x）］2-［f（x）］2=1。

（2）f（2x）=2f（x）·g（x）。

（3）g（2x）=［g（x］2+［f（x）］2。

所以［g（x）］2-［f（x）］2=［g（x）+f（x）］［g（x）-f（x）］

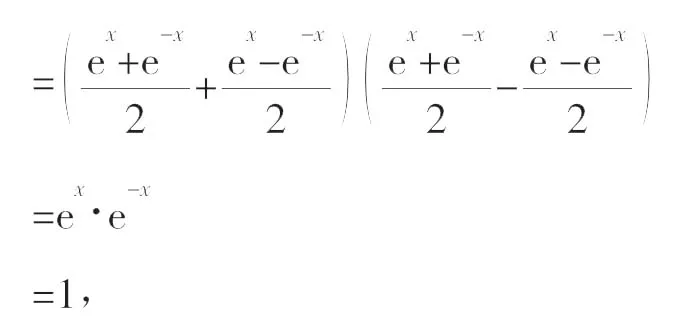
原式得证。

所以f（2x）=2f（x）·g（x）。

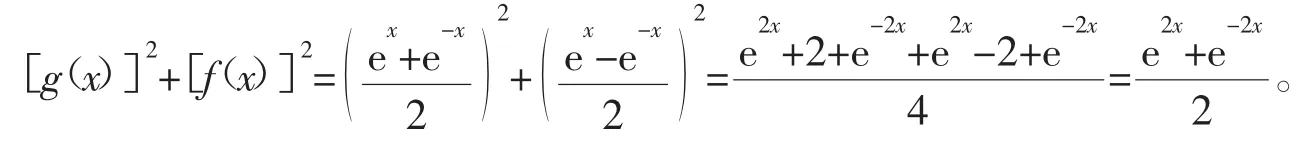
所以g（2x）=［g（x）］2+［f（x）］2。