促进理解感悟本质
2016-10-29刘晓萍
刘晓萍
【设计理念】
小数起源于生活中的测量和部分与整体的关系。当一个单位量被等分为十份、百份、千份等10的倍数份时,就可以用小数来表示。因此,小数常常被看作特殊的分数(分母为10及10的倍数的分数)。其实,小数与分数还是有区别的。首先,从知识形成的历史来看,分数和小数形成的过程并不相同。在度量过程中,当整数已经不能完全精确地表示实际数量时,就逐渐形成两种表示方法:一种是用分数来表示不满“1”的部分;另一种是发展度量衡系统,采用更小的单位来表示不足整数的剩余部分,这就是小数的由来。其次,计数的方式不完全一样,分数是由分数单位组成的,小数则采用整数的十进位结构与计数规则,也就是用0~9十个数字配合位值概念来计数,因此,小数可以看作整数计数方式的延伸(向越来越小的方向)。第三,分数与小数的运算方式不完全相同。美国数学史家卡约利认为:十进小数是近代数学史上关于计算基础方面的三大发明之一。
了解小数的发展历史能给我们的教学以启示。一是为了更好地让学生理解小数的意义,教学中既要突出小数的本质内涵,不能将小数的意义等同于分数的意义来教,又要注重小数与分数的联系。二是要注意知识的结构化,重视小数计数方式与整数计数方式的统一,帮助学生建构完整的知识结构,尤其要注意小数的单位以及小数数位概念的形成与发展。三是小数的发展历史告诉我们,小数来源于生活实践,在教学中要注意创设合适的情境,让学生自主探索、经历知识的创造过程和数学化过程,并充分体悟数学知识背后的思想和方法。
教材第一课时安排了2个例题,还有“想想做做”。例1创设了两个小朋友测量桌椅长度的情境,呈现整数部分是0的一位小数;例2创设了购物的情境,呈现整数部分不是0的一位小数。教材比较注重小数与分数的联结,两个例题都强调不满“1”的部分是十分之几,又可以写成零点几。从学生理解的角度来看,仅仅这样教学是不够的。为了促进学生对小数意义的理解,教师至少还应该思考这样几个问题:为什么要有小数?小数与分数完全一样吗?学生学习小数有哪些认知基础和生活经验?如何通过多维表征来深入理解小数的意义?等等。
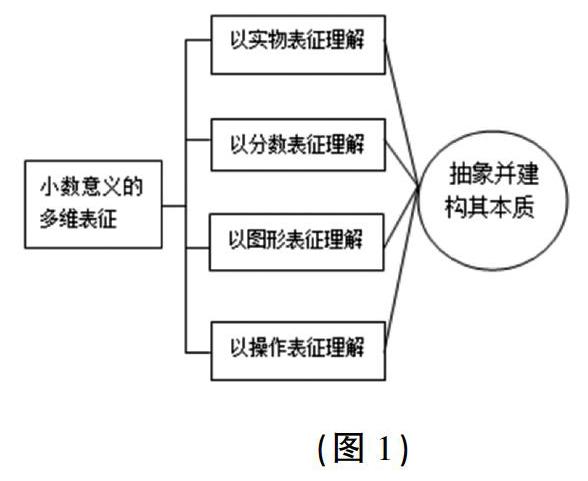
有了这些对知识背景的分析和理解,我从下面几个方面展开了教学设计:一是从学生已有的生活经验开始,让学生发现生活中小数的应用;二是通过小组合作,共同研究小数的意义,学会发现、提出、分析和解决问题的方法;三是通过多维表征,加深学生对小数意义的理解(如图1)。
【教学目标】
1.学生结合具体情境认识小数,能识别小数,会读写小数。知道以元为单位、以米为单位的小数的实际含义。知道小数数位的意义。
2.学生通过测量和等分,感知小数与分数的联系,初步感知十分之几可以用一位小数来表示。培养学生解决简单的实际问题的能力。
3.学生经历小数形成的过程,以及列举生活中小数实例的过程,感知数学与生活的密切联系,培养学生学习数学的兴趣。
【教学活动及意图】
一、以生活为起点,发现小数
1.出示超市中文具的价格。
钢笔21元 橡皮0.5元 铅笔1.2元
2.让学生比较价格的不同,初步感知小数。
3.在生活中,你还见到过哪些小数?
预设:(1)每天的气温。(2)报纸上的一些数据。(3)物品的质量或长度……
【学生在生活中经常会接触到小数,且具有十进制计数方法和十进分数的意义等知识基础。本环节尊重学生的已有认知经验,有意识地培养学生发现问题和提出问题的能力。】
二、在具体情境中研究小数
1.以橡皮的价格0.5元和讲台的长度1.2米为例,研究0.5和1.2的意义。
2.学生谈自己的发现,教师引导:
(1)画图表征:引导学生以一个长方形(或一条线段)表示1元或1米,分别表示出0.5和0.2。
(2)思考:用一个长方形表示出0.5和0.2的相同之处和不同之处。
(3)分数表征:把一个物体平均分成10份,表示其中的几份还可以用分数来表示。思考0.5和0.2分别可以用怎样的分数来表示。分别说说它们的意义,体会一下零点几和十分之几的联系。
3.初步应用。
(1)实物表征:1.8元和0.1元分别表示几元几角?
(2)说一说:5元2角和1米4分米分别可以用怎样的小数来表示?
【充分利用学生的已有认知,引导学生在问题解决过程中逐步认识小数的意义。为了让学生深入理解概念,教学中采用语言表征、实物表征、分数表征、画图表征等多维表征方式,让学生逐步建构小数的本质内涵,并上升为以符号表征为主的形式化理解。此外,多维表征方式还可以让学生建立良好的数感,通过数学去理解生活、提升数学素养。】
三、在操作表征中深化理解
1.创设购物情境。爸爸带晓杨去商场买电脑,电脑的价格是2433.5元。
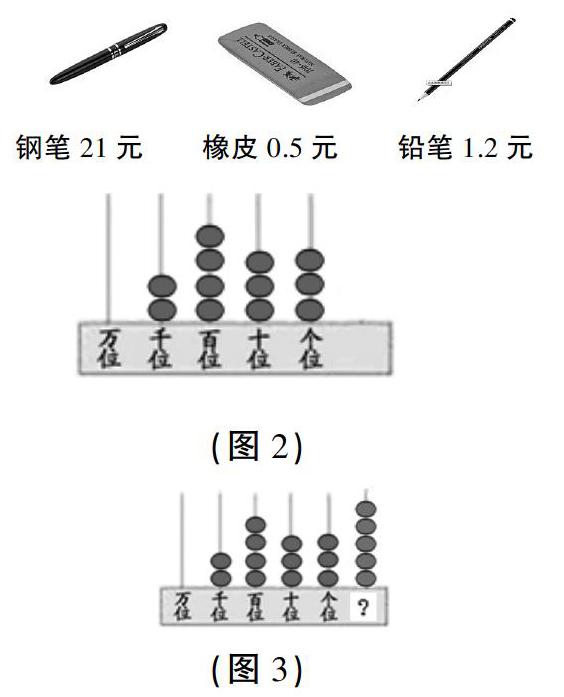
2.请学生在计数器(如图2)上表示出2433元,并说说各个数位上的数表示什么意思。
3.小组讨论:0.5元怎么在计数器上表示出来?
(1)引导学生思考:整数计数时,满十向前进一位,如果没有数位怎么办?
(2)0.5表示什么意思?如果要在计数器上表示,它的数位应该在哪里?为什么?想一想,0.5里有几个0.1?
4.学生交流。根据0.5的意义,它的数位应该在个位的右边,鼓励各小组学生为这个数位起个名字(如图3)。
5.根据计数器读一读、写一写。学生在读写过程中可能会出现问题,如计数器上没有小数点,学生可能读到小数部分时不知道怎么读了,此时,可以让学生思考:如果没有数位标记,怎么来区分个位和十分位?
6.学生交流想法。教师顺势介绍小数的发展历史以及计数方法的由来。在小数的记法中,用于区分整数部分与小数部分的记号称为“小数点”,这个记号至今还没有统一,我们国家用“.”来表示,欧美一些国家则用“,”来表示。
【本环节是在学生初步感知小数的基础上,通过操作表征来完善他们对小数意义的理解。学生对数学知识的理解,主要是通过自己不断反思和感悟得到的,促进理解的数学学习是建立在深刻理解相关知识及其经脉的基础上的。整数的计数方法已存在于学生的认知结构中,在教学中,要充分利用这个基础,让学生创造小数的计数方法,创造出新的数位和小数点,使其原有认知与新的概念形成一个新的认知系统,从而深刻理解小数的意义,也让学生感悟到创造数学的魅力。】
四、在拓展延伸中丰富内涵
1.填一填。
(1)5个1和6个0.1合起来是( )。
(2)10个0.1是( )。
(3)18个0.1是( )。
(4)4.8是( )个0.1。
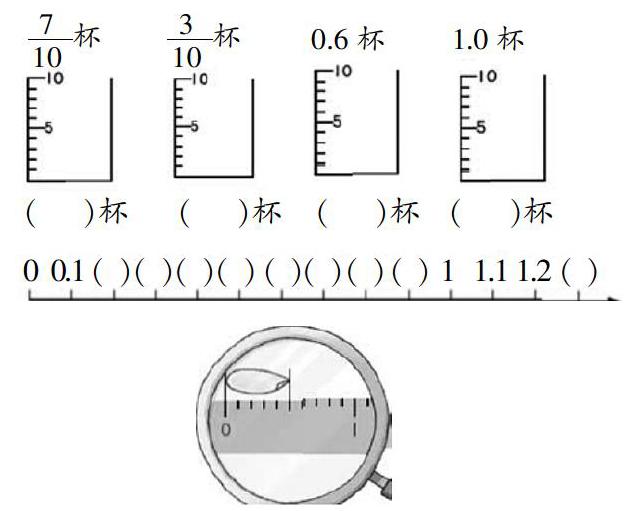
2.涂一涂:请用彩色笔在量杯上涂出指定水的高度,并在( )填上小数或者分数。
3.看图回答问题。
(1)把数线上0~1平均分成10格,1格是多少?
(2)在( )里填上小数。
(3)从0到0.9共有几格?
(4)从0开始往右数13格是多少?
4.思考:宗伟测量一粒大米,大米长约5毫米,可以写成多少厘米?
你会把它写成多少分米吗?在计数器上又怎么来表示呢?有兴趣的同学可以跟爸爸妈妈一起研究研究。
【练习设计分为四个层次,分别是为了增强学生对小数概念不同层次的理解和能力而展开的。第一层次的设计强调小数的单位,这不仅是认识小数的基础知识,也是在为接下来学习小数大小比较和运算打基础。第二层次的设计是进一步联结小数与分数的意义,通过操作表征进一步沟通十进分数与小数之间的联系。第三层次的设计共有四问,第一和第二问是通过在数线上表示小数,进一步理解小数的意义,沟通小数与整数的联系,渗透小数是数系统发展的思想,后面两问是直观地表示出小数加法和加法计算的原理,为小数的四则运算作算理上的准备。第四层次的设计是对初步认识小数的拓展,把5毫米表示成多少厘米,是已学的一位小数,把它表示成多少分米,则是两位小数了,如果把两位小数表示在计数器上,还要创造新的数位。提出这一具有挑战性的学习任务,是基于两方面的考虑:一是有意识地让学生将认知和创造一位小数的经验迁移到两位小数的认识上;二是为以后学习多位小数作铺垫。】
(作者系江苏省苏州市教育科学研究院小学数学教研员)
