把“学”放到教学的中心位置

贲友林

【设计理念】

建构“学为中心”的课堂，是我国当下课堂教学变革的基本取向。“学为中心”的课堂，是指以学生学习活动作为课堂教学过程的中心或本体的课堂。在“学为中心”的课堂中，学生能动地、自主地学习成为其学习的基本状态，占据主要的教学时空。教学“正比例和反比例”，我想：如果教师不教，先让学生学习，学生会学得如何呢？如果没有教师，只有教科书，学生能不能学习？如果能，那学生能学会什么？能学到什么程度？反思我们的教学，学生能学了，我们放手让学生学了吗？当学生自主学习了，他们达成我们预设的教学目标了吗？在学生自主学习后，教师的教学又该如何推进呢？

基于上述追问，我对“正比例和反比例”的教学做了一些尝试：一是将“正比例和反比例”安排在一节课中学习；二是组织学生在课前先自主学习“正比例和反比例”；三是调整教的方式，进退之间，依学而教。我以为，这样教学，可以更从容地从学生“学”的角度组织练习，关注并处理学生在认识正比例、反比例过程中出现的各种“问题”。

反思往常的教学设计，往往看到教师却难见学生，关注了“教”却忽视了“学”。过度的“教”的设计，逼仄了学生学的时间与空间，窒息了学生的思维和智慧，压抑了学生自主学习的兴趣与热情。把“学”放到教学的中心位置，意味着把学的时间与空间还给学生，意味着学生可以应用多种学习方式展开自主学习，让学习看得见。看得见的学习，不是学生跟在教师后面亦步亦趋，而是他们自主地往前走，教师与学生相伴而行。如此课堂，从“为教师的设计”走向“为学生的设计”，进而走向“和学生一起设计”。把“学”放到教学的中心位置，意味着课堂成为基于学生的学习、展示学生的学习、交流学生的学习、深化学生的学习的真正的“学堂”。如此“学为中心”的课堂，是我们所期待并且能够实现的“另一种可能”。

【教学目标】

1.经历从具体实例中认识成正比例、反比例关系的两种量的过程，初步理解正比例、反比例的意义。

2.在认识成正比例、反比例关系的两种量的过程中，初步体会数量之间相互依变的关系，感受有效表示数量关系及其变化规律的不同数学模型，提高分析、抽象、概括、推理能力，渗透初步的函数思想。

3.在主动参与数学活动的过程中，感受数学思考过程的条理性，并乐于与人交流。

【教学活动及意图】

课前，学生独立、自主完成如下“研究学习”材料：

（1）什么叫正比例？举例说明。

（2）什么叫反比例？举例说明。

（3）比较成正比例关系的两种量和成反比例关系的两种量，我的发现——

（4）关于“正比例和反比例”，我的总结——

（5）关于“正比例和反比例”，我的疑问——

【在没有组织学生学习正比例、反比例之前，学生对于正比例、反比例不是一无所知。课前组织学生进行研究学习，这既是一种学习内容的安排和学习任务的明确，又是对学生学习方法的指导，即教师在“教”学生思考、研究的路径，也为学生提供了课堂交流的线索。与学生按照有关提纲与问题对相关内容作探索性理解“在前台呈现”相对照的是，教师先进后退，教师的“教”退到了幕后。】

一、揭示课题

谈话：今天这节课，我们探讨有关正比例和反比例的知识。

二、组内交流学习

继续谈话：在课前，我们已经对“正比例和反比例”进行了研究学习。请大家在小组里，就“研究学习”材料中的问题进行交流，一会儿我们用抽签的方式选择与全班交流的小组。

学生按4人一小组进行交流。

【学生自主学习之后，教师组织学生在课堂上进行交流学习。两个层次的交流互动学习，对学生来说是两轮学习。第一轮是组内交流学习。每位学生在小组内要将自己课前研究过程中的想法与困惑、发现与疑问和盘托出。之后，小组成员商讨，如果我们这个组在全班交流，如何整合小组内各人的想法，如何分工将小组的学习成果向全班介绍。第二轮是全班交流学习。由一个小组在全班主讲，其他小组的学生先听后讲，也就是听完该小组的讲解之后，再陈述各自的想法。用抽签的方式产生与全班交流的小组，其意图是让所有的学生意识到，每个小组都有可能也有能力与全班交流。】

三、全班交流学习

用抽签的方式产生与全班交流的一个小组。

1.组织交流“正比例”。

交流“研究学习”材料第1题。预设：小组中的第一位学生会和全班交流“正比例”。学生可能照搬教材中的例子，然后介绍路程和时间是两种相关联的量，时间变化，路程也随着变化，当路程和相对应的时间的比的比值一定时，行驶的路程和时间成正比例关系。

教师追问：“关联”是什么意思？为什么说路程和时间是两种相关联的量？能举例说说其他相关联的量吗？ 结合学生的回答，教师出示相关例子，学生辨析：

（1）练习本的本数和练习本的总价。

（2）汽车行驶的速度与时间。

（3）考试试卷中的得分与失分。

（4）学生的身高与数学考试的成绩。

讨论：成正比例关系的两种量有什么特点？

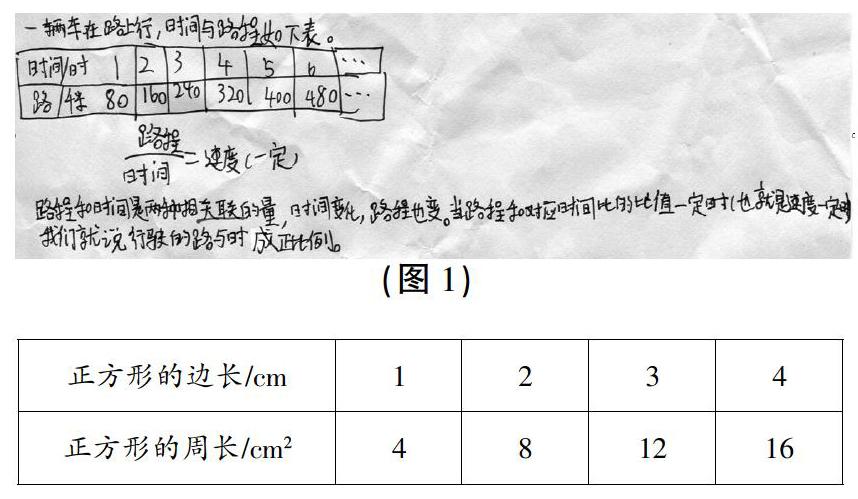
学生可能用表格呈现时间和路程的数据（如图1），并说明其比值一定。教师引导学生横着看表格，发现了什么？竖着看表格，发现了什么？横着、竖着联系起来看，发现了什么？

引导小结：通过观察和计算，我们对路程和时间的关系有两点发现：一是路程和时间是两种相关联的量，也就是时间变化，路程也随着变化；二是路程和对应的时间的比的比值一定（也就是速度一定）。具备了这两个条件，我们就可以得到结论：行驶的路程和时间成正比例；行驶的路程和时间是成正比例的量。

组织学生补充：还有哪些成正比例的量？再举例说一说。

辨析：所举的例子是否正确？

引导比较：不同的例子，为什么都说它们成正比例关系？

2.组织交流“反比例”。

交流“研究学习”材料第2题。教师提出交流要求：想一想，“正比例”是怎样交流的，能像交流“正比例”一样交流“反比例”吗？

交流过程中，组织学生质疑。教师穿插追问：（1）怎么看出这两种量是相关联的量的？（2）这两种相关联的量的变化有什么特点？

学生补充举例，交流不同的成反比例关系的两种量。

3.交流“比较”。

交流“研究学习”材料第3题。在学生交流的过程中，指导学生按这样的问题即提纲进行比较：成正比例的两种量与成反比例的两种量，相同点是什么？不同点是什么？

结合学生的回答，引导学生梳理：都是相关联的两个变量，变化趋势或相同，或相反；变化过程中保持其比值不变或积不变。

如果学生未出现用字母表示成正比例关系与成反比例关系的两种量，教师就提问：能否用含有字母的式子表示？

追问：式子中的x、y、k分别可能表示什么？

教师引导学生举例交流。教师预设如下例子，学生辨析。

（1）正方形的边长和周长统计如下表：

x表示正方形的边长，y表示正方形的周长，正方形的边长与周长成正比例关系。

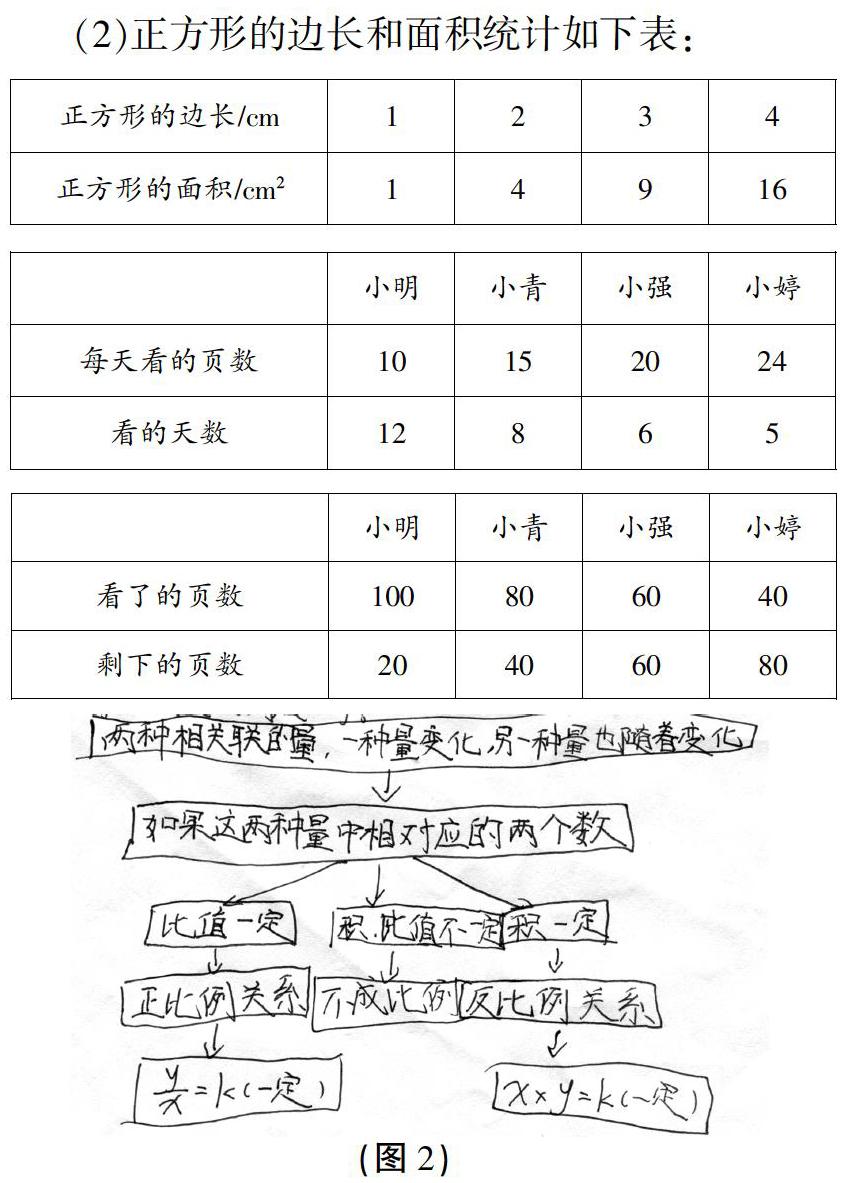
（2）正方形的边长和面积统计如下表：

x表示正方形的边长，y表示正方形的面积，正方形的边长与面积成正比例关系。

（3）小明、小青、小强、小婷都买了一本《数学家的故事》，每人每天看的页数和看的天数统计如下表：

x表示每天看的页数，y表示看的天数，每天看的页数与看的天数成反比例关系。

（4）小明、小青、小强、小婷都买了一本《数学家的故事》，每人看了的页数和剩下的页数统计如下表：

x表示看了的页数，y表示剩下的页数，看了的页数与剩下的页数成反比例关系。

（5）明明3岁时体重12千克，11岁时体重44千克。x表示岁数，y表示体重，明明的体重和身高成正比例关系。

进一步思考：两种量，不成正比例关系就成反比例关系，对吗？

【学生通过自己的阅读，能模仿着说教材中的结论语，学生是否真正理解这样的表述？正比例、反比例的概念比较抽象，学生自己学习时通过对例子的抽象，对正比例、反比例往往似懂非懂。学生的认识从常量走向变量，不再将量作为一个固定不变的数，这时的认识尚未达到真正的理解。教师的教学策略是让学生再举例，利用例子实现具体化的理解。

从所学内容来看，小学阶段教学正比例和反比例的关系，并不出现函数概念，只是让学生具体感知两种量之间的关系，既能使学生对数量关系的认识和理解更加丰富，又能为他们到中学进一步学习正比例函数和反比例函数以及一般的函数知识作准备。因而，教学应与实际情境紧密联系，通过具体的例子，用学生可以理解的方式呈现，引导学生从具体数量关系的角度，结合两种量之间的变化规律理解和掌握这一内容。

从学生学习的过程来看，学生用正例阐述自己对正比例意义、反比例意义的理解，教师让学生补充举例，或许学生举例中的错误恰好成为反例，但学生所举的反例不一定全面、典型，教师相机穿插自己的备份。在这一系列学习活动中，学生慢慢体验、感悟，逐渐增强对概念本质属性的认识与理解。在学生展示、交流的过程中，教师相机穿插追问、引导，将学生的理解引向深入。】

4.交流“总结”与“疑问”。

交流“研究学习”材料第4题。预设学生有如图2所示的整理。

展示给全班学生，并让学生进一步分析：你看懂了什么？这样的总结，值得你学习的是什么？

结合学生的总结，组织学生回顾课前“研究学习”材料中的“疑问”，反思：这些疑问是否已经解决？如果还没有解决，现在提出来与全班探讨。

如果学生没有提出下面的问题，教师则相机提出：正比例、反比例研究的是什么？正比例、反比例与比例是什么关系？并将这些问题作为学生课后研究的问题。

【通过展示学生的优秀作品，让其他学生在赏析的过程中学习如何总结。之后的反思，每位学生在内心“对照”的过程中体验学习进益，而对未解之疑的交流，又为学生进一步思考、学习打开了大门。当教师放手让学生学习之后，教师并不是撒手、放任、不作为。教师或进或退，依学而教，教师的教表现得更为灵活与机敏。教师的教，提示学，引导学，组织学，提高学，欣赏学，即，服务学生的学，促进学生的学。】

（作者系南京师范大学附属小学数学教师，江苏省数学特级教师）