一次奇妙的再创造之旅

2016-10-29陈一叶

江苏教育 2016年15期

陈一叶

《认识小数》是苏教版三下的教学内容。学生在认识小数之前，已经对小数的意义有一定的生活经验和知识基础。学生在现实生活中经常能见到小数，如文具的价格、食物的价格等；学生学习小数的知识基础是整数的十进制计数方法和分数的意义。

新课标提出，要让学生“经历从日常生活中抽象出数的过程，理解万以内数的意义，初步认识分数和小数”。心理学研究表明：儿童获得概念的方式主要是概念的形成和概念的同化。前者主要依靠对具体事物的概括获得概念，后者主要利用认知结构中相关的原有概念来理解新概念。随着学生对知识的积累，概念的同化逐渐成为他们获得概念的主要方式。学生学习小数应该属于概念的同化。但问题的关键，是如何找到用来同化小数这个概念的系统结构。

从学生已有的认知结构来看，有两种方式可以抽象出小数的概念。一种是从十进分数入手，一般认为小数是十进分数的另一种表示形式，所以教材都是先安排认识分数，再安排认识小数。元、角、分是小数在生活中的原型，教学时都会利用这个资源，通过生活经验（零点几元）和知识经验（十分之几）的对接，让学生知道零点几就是十分之几。另一种是从整数计数方法的知识结构出发，把小数看作整数计数的概念推广，也就是基于十进制表示数量的需要，以前学生学习的整数计数是往大的方向发展的，即满10个计数单位就往上面一级进1，但由于生活和数学的发展要求，计数也要往另一个方向（即越来越小的方向）发展。

由此，我们知道，小数与自然数一样，都是用来计量的，是生活中很多时候不能用自然数计量时产生的新数，它也遵循十进制位值系统的一切规则。张奠宙教授指出：小数是十进制计数沿着另一个方向（越来越小）的延伸，不是分数的附庸。

从数学史的角度来看，分数和小数的产生其实是相对独立的，我国古代刘徽最早提出十进小数的概念，实质上就是十进制计数的发展。国内外教材对“认识小数”的编排也有两种不同的方式：一种是从小数与十进分数的联系来编排的，如我国的教材；另一种是从整数计数的推广角度来编排的，如法国的教材。

基于上述分析，教学时，我采用十进制计数与分数意义相结合的方式，创设古人计数的情境，让学生经历小数的产生过程，通过独立思考和小组合作的方式“再创造”出小数，并逐步抽象出小数的意义。用学生已经熟悉的十进制位值系统的知识结构来同化小数的概念，对学生来说，更容易理解小数的意义，因为这对其知识结构的构建来说，不仅能凸显小数的本质，也是十进制位值系统完善的需要；从另一个角度讲，分数的意义也是小数意义的基础。由此，在教学中，我充分利用学生已有的分数意义的基础，这样，学生能更完整地认识小数的本质。

【教学目标】

1.结合具体情境，使学生经历初步抽象出小数概念的过程，体会小数的意义，体会小数产生的必要性。

2.会读、写小数部分是一位的小数，知道小数各部分的名称。

3.培养学生互相合作、互相交流的能力，激发学生学习数学的积极性，提高学生学习数学的兴趣。

教学重点：使学生经历初步抽象出小数概念的过程，理解小数的意义。

【教学活动及意图】

一、呈现结构，唤醒旧知

1.谈话导入结绳计数。

今天，老师带来了一位大家的好朋友（出示哆啦A梦图片），哆啦A梦有一个神奇的时光机，可以穿越时空。让我们一起跟着他来到一个原始部落。（播放视频）这个原始部落里的人以打猎为生，有一次，他们打到了一些猎物。（出示猎物情境）

师：同学们猜猜看，古时候的人是怎么知道打了多少只猎物的呢？（结绳计数、用小石子计数）

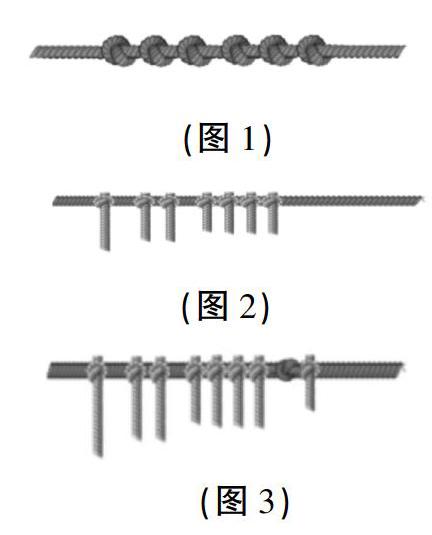
师：是的，古时候计数的方法很多，这个部落是用绳子打结来计数的。（出示结绳计数场景，出示图1）你知道这表示几只猎物吗？

2.怎么来表示很多猎物？

师：猎物越打越多，打一只猎物就要打一个结，非常麻烦，于是他们想到了一个办法。你知道是什么办法吗？（满十只打一个大一些或者长一些的绳结）

出示图2，这表示多少只猎物呢？（124只）

3.在计数器上画一画、写一写。

师：同学们真了不起，一下子就明白了古人的意思！请你在计数器上画一画，并写下这个数。

师：与古人相比，你感觉我们现在的计数方法怎么样？（方便、清楚、容易）

4.假如猎物储存到十个一百只，在这个绳子上怎么来表示？（在百前面加一根更长一点的绳结）

【十进制位值系统有两层含义：一是“满十进一”；二是同一个数字在不同的数位上表示不同的数值。本片段十分生动地勾画了十进制位值系统发展的历史，唤醒了学生已有的知识积累。通过了解古代计数方法并与现代计数方法进行比较，再现十进制的知识结构，为学生接纳小数的概念作好了铺垫。】

二、自主探究，初步建构

1.把1只猎物平均分成10份，其中的1份在绳子上怎么表示？

师：有一次，部落里来了客人，他们正好打到了一只猎物，于是把这只猎物拿出来平均分成10份，用其中的9份去招待客人了，还剩下其中的1份，你会在图2的绳结上把这1份记下来吗？

同桌讨论交流，学生自己尝试记录，之后反馈交流。

生：我在1只后面再画一根更短的绳结。

师：这根更短的绳结表示什么意思？

生：表示把1只猎物平均分成10份，其中的1份。

师：想法非常棒，但老师有个疑问，假如一个不了解的人，怎么知道哪个表示1只，哪个表示（1只）10份中的1份呢？你有办法区分吗？

生1：这个（1份）绳结离那个（1只）绳结远一点。

生2：在1只和1份之间作一个记号。

师（出示图3）：好办法！原始部落的人也是这么做的，在1只和1份之间再打个结区分一下。

2.怎么在计数器上表示1份？

师：原始部落的人会用绳结上表示1份了，你能不能在刚才表示124的计数器上把这个10份中的1份表示出来呢？

小组讨论，尝试“创造”出小数。

生1：我们小组发现原来的数位上不能表示这10份中的1份了，怎么办呢？我们就在个位的右边又添了一根线，在上面画一颗珠子就表示10份中的1份了，我们给这个新的数位取名叫“分位”，因为它是平均分出来的。

生2：我们也是这样想的，只不过我们给这个数位取名为“份位”，因为它上面的一颗珠子表示的是1份。

生3：我们取名叫“十分位”，因为是把1只猎物平均分成10份，表示其中的1份。

师：同学们的想法非常棒，自己创造出了一个新的数位。那怎么跟原来的个位区分呢？

生1：我在这两个数位中间画一小竖作个记号。

生2：我画了一个点，这样更简单。

师：同学们的想法跟数学家创造的非常接近，现在我们又创造了一个新的数位，这个数位叫十分位，它表示把1平均分成10份。为了区分1个和10份中的1份，我们在这里用一个小圆点区分开。（课件演示十分位的产生过程）

3.认识小数。

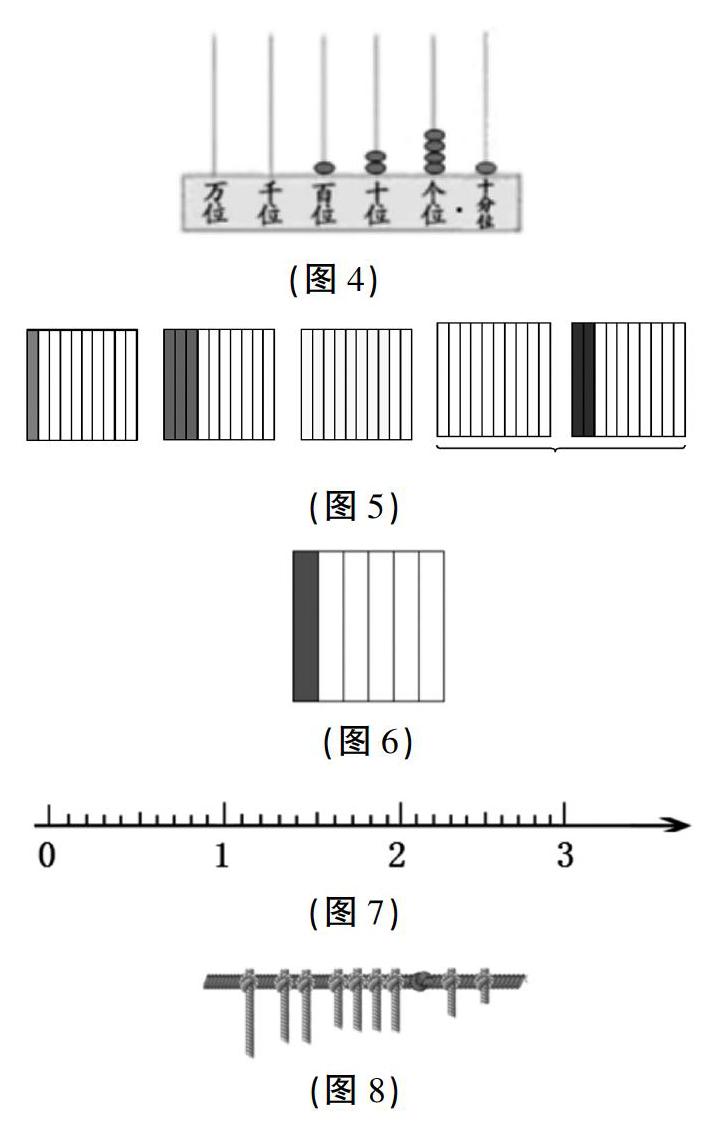
师：把计数器（如图4）上的数完整地写下来。（学生写一写124.1）

师：这样的数叫什么数？（揭示课题：认识小数）关于小数的知识还有很多，请自学教材第88页的一部分内容。

学生交流124.1这个数各部分的名称，并一起来读一读。（板书：整数部分，小数部分，小数点）

4.认识0.1。

师（出示表示0.1的计数器）：你能写出这个数吗？它的整数部分是多少？小数部分呢？0.1表示什么意思？

表示这样的3份是多少呢？（0.3）0.4，0.5……0.9（十分位上的珠子依次增加）再加一颗呢？（往前进一，也就是说10个0.1是1）

出示两个计数器（分别表示36.6和0.4），让学生写一写、读一读、说一说，整数部分和小数部分分别是多少？36.6中的2个6分别表示什么意思？

5.回顾总结。

师：学到这里，你对小数有了哪些认识？怎么会出现小数的？

【小数的产生是生产和生活中计量的需要。这个片段的教学，引领学生真正经历了小数产生的过程，弗赖登塔尔说：学习数学唯一正确的方法是实行“再创造”。通过让学生自己创造出小数，一方面，可以加深他们对小数概念的理解；另一方面，可以让他们感受到，十进制的位值系统除了可以向越来越大的方向发展，还可以向相反的方向发展，这是对原来计数方法的一次重大突破。】

三、逐步深化，系统建构

师：同学们，你们在生活中见到过小数吗？

1.大自然中的小数。

（出示：蜂鸟的重量1.8克，蜂鸟蛋的重量0.2克）提问：1.8的整数部分是几？小数部分是几？0.2表示什么意思？

2.超市中的小数。

铅笔0.5元 0.5元=（）角

橡皮9角 9角=（）元

文具盒8.4元 8.4元=（）元（）角

计算器25.6元 25.6元=（）元（）角

反馈时追问：为什么0.5元是5角？9角为什么是0.9元？8.4和25.6的整数部分表示什么？小数部分呢？

3.图形中的小数。

（2）出示图6，可以用0.1来表示吗？为什么？