基于经验模态分解重构的二次相关时延估计*

周卓伟，孙山林，李 云，陈庞森，申静文

（1.桂林电子科技大学信息与通信学院，广西桂林　541004；2.桂林航天工业学院电子与信息自动化学院，广西桂林　541004）

基于经验模态分解重构的二次相关时延估计*

周卓伟1，孙山林**2，李 云2，陈庞森1，申静文2

（1.桂林电子科技大学信息与通信学院，广西桂林541004；2.桂林航天工业学院电子与信息自动化学院，广西桂林541004）

针对低信噪比情况下的时延估计，将二次相关（SC）时延估计与经验模态分解（EMD）算法结合，提出了EMD重构二次相关时延估计方法。该方法针对EMD重构时本征模态函数的选择，将倒谱法和谱减法相结合，提出新的本征模态函数中有用信号主导分量和噪声主导分量的区分方案。研究结果表明：EMD重构二次相关法较传统二次相关法抗噪性能更优，更能锐化二次相关峰值；在非高斯有色噪声和高斯白噪声情况下，分别将准确估计时延的信噪比降低了4 dB和2 dB。

时延估计；经验模态分解；二次相关；声音定位

1　引　言

作为声源定位的关键技术，声达时延估计一直是信号处理领域研究的热点问题［1］，并已被应用于水下目标跟踪与定位［2-3］、卫星干扰源定位［4］、智能机器人［5］等多种场合。而传统的时延估计方法如广义互相关（Generalized Cross Correlation，GCC）法［6］、自适应最小均方滤波法［7］、最小二乘（Least Squares，LS）法［8］等，在没有噪声影响时能够达到最佳估计，但当存在实际噪声干扰且信噪比较低时，估计的准确性会大大降低，因此提高时延估计的抗噪性能十分重要。针对低信噪比的情况，文献［9］中提出的二次相关（Second Correlation，SC）法具有一定的抑制噪声和多径反射干扰的能力。之后，文献［10］中提出的广义二次相关（Generalized Second Cross-Correlation，GSCC）法和文献［11］中提出的小波变换二次相关（Wavelet-SC）法又对SC法在低信噪比条件下的抗噪性能做了改进。但要进一步提高SC法在更低信噪比下时延估计的性能，可考虑对接收信号进行适当的降噪处理。而在众多噪声抑制算法中，经验模态分解（Empirical Mode Decomposition，EMD）方法是处理非线性、非平稳信号最好的降噪算法之一［13］，它不像自适应滤波那样依赖于滤波器的阶数［14］，而且EMD方法与小波变换、短时傅里叶变换、Gabor展开等传统的分析工具相比，不需预先设定基函数，而是得到一个依赖于信号本身的自适应广义基，对不同信号进行分解会得到不同的基函数［13，15］。不过，要使用EMD方法进行降噪处理，还要解决在EMD重构时本征模态函数（Intrinsic Mode Function，IMFs）的选择问题。

本文结合EMD方法与SC法，提出一种新的EMD-SC方法，在SC法的基础上，进一步提高了低信噪比情况下声达时延估计的准确性；通过倒谱分离、谱减法，实现了EMD分解后有用信号主导IMFs的选择；在不同信噪比下，通过仿真比较了SC法、GSCC法、Wavelet-SC法与EMD-SC法的性能，结果表明EMD-SC方法在时延估计方面具有较强的抗噪能力和较高的估计准确率。

2　构建时延估计模型

在波的研究过程中，常常假设其传播是以球面波的形式进行的。但是在声达延时估计模型中，为了研究的方便，一般假想声源与需要估计声达时延的两接收端位于同一平面，把问题从三维转换到二维。理想情况下，假设声源发出声波信号为s（t），则

式中∶yi（t）（i=1，2）为接收信号；ni（t）、αi分别为加性噪声及衰减系数；T为观测时长；σ为两接收信号之间的时延。分别对y1（t）进行自相关，y1（t）、y2（t）进行互相关，得到一次相关模型∶Ry1y1（τ）=E｛y1（t）y1（t+τ）｝=

根据自相关函数的性质，Rss（τ）与Rn1n1（τ）在零点处有唯一峰值，Rss（τ-σ）在τ=σ处有唯一峰值。再根据互相关函数的性质，因为忽略噪声与信号之间的相关性，Rss（τ-σ）与Rss（τ）、Rn1n1（τ）进行互相关后，得到的峰值都在τ1=σ处。因此，时延估计值为

3　EMD-SC时延估计方法

EMD方法把加噪语音信号分解成不同的本征模态函数（IMFs）分量，其中阶数较低的IMFs为信号的高频成分，且每个分量的信噪比不同。如果选择出有用信号主导的IMFs，再将它们进行重构，能够有效地降低接收信号中所含噪声成分，进而提高二次相关时延估计的准确性。EMD-SC法的原理框图如图1所示。

图1　EMD-SC法原理框图Fig.1 The principle block diagram of EMD-SC method

3.1谱减法获取高信噪比频段

3.1.1语音信号倒谱分析

对于任意语音信号的采样序列假设为y（n），计算其倒谱的方法如下∶将y（n）进行傅里叶变换得到Y（ω），将Y（ω）的幅值取对数得到（ω），再对（ω）进行傅里叶逆变换就得到倒谱序列（n），即

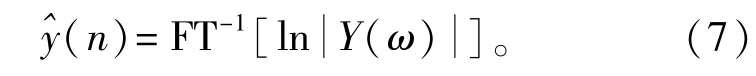
因为语音信号都是由声门脉冲激励u（n）经声道响应v（n）滤波得到（不考虑口唇辐射）［13］，即语音信号y（n）可以表示为脉冲激励与声道响应的卷积∶

将式（8）两边进行离散傅里叶变换得到

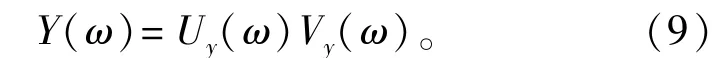
再将式（9）代入式（7）中，可得到

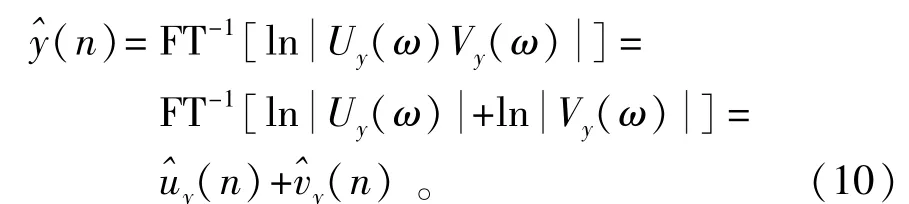
针对语音信号，声道模型通常被视为一个谐振腔，声带振动时对应谐振腔的谐振频率会产生共振，得到较高的语音信号能量，因此，理论上在噪声频谱均匀分布的前提下，处于谐振频率附近的频段会含有较高的信噪比。而实际上噪声频谱并非均匀分布，只有通过用含噪语音信号对应的声道响应频谱与背景噪声对应的声道响应频谱进行噪声对消，才能消除由于噪声频谱分布不均匀产生的影响，因此考虑采用谱减法进行噪声对消。但使用谱减法还存在两个问题∶首先，背景噪声频谱并非先验可知；其次，在式（8）中，声道响应vy（n）的频谱包络才能反应声道谐振频率的分布，为了确定语音的谐振频率段，需要从y（n）中分离出vy（n）。

针对背景噪声频谱并非先验可知的问题，因为背景噪声在短时间内所含的频率成分变化不大，而进行一次时延估计截取的一帧语音信号的长度足够短，可以认为接收信号的前导（无话段）噪声信号近似为接收语音背景噪声信号。此外，式（10）说明在倒谱域中声门脉冲激励和声道响应是相对分离的，利用倒谱特性在倒频率轴上设置矩形窗可以实现式（8）中声道响应vy（n）与脉冲激励uy（n）的分离。

3.1.2谱减法获取高信噪比频段的具体方法

对式（1）两路接收信号中的第一路信号对应的前导噪声信号b1（t）和语音信号y1（t）进行采样，得到离散序列b1（n）与y1（n），长度为N。利用式（7）～（10）得到倒谱1（n）和1（n）∶

在倒频率轴上设置矩形窗函数window（n），窗宽为n0∶

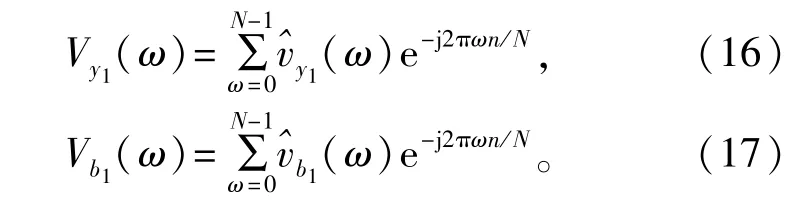
将频谱包络线Vy1（ω）与Vb1（ω）按式（18）做差消除对等噪声，并除以瞬时噪声能量Vb1（ω）2，得到谱差曲线D1（ω）∶

谱减法得到的归一化谱差曲线¯D1（ω）能反映含噪语音信号对应的声道响应频谱与背景噪声对应的声道响应频谱进行噪声对消后谐振频率的分布情况，因此，¯D1（ω）对应幅度越大的频段具有较高的信噪比。利用门限法获取¯D1（ω）归一化幅值高于T1（实验中取值为0.8）的频段，假设满足条件区域有k个，对应频段记为［ωp1，ωq1］，…，［ωpk，ωqk］，即为接收信号y1（n）信噪比较高的频段。此外，因为实际声源定位中，由于要满足空间采样定理，两接收端的距离通常很近，可以认为接收信号y2（n）与y1（n）对应的高信噪比频段相同，不必要对第二路信号进行重复处理。

3.2信号重构并估计时延

对接收信号采样序列yi（n）（i=1，2，n=1，2，…，N）中第一路接收信号y1（n）进行EMD分解，依次得到m个基本模态分量（记为h1（n），h2（n），…，hm（n））和一个分解后的余量rm（n）。这样y1（n）就可以表示为基本模态分量和余项的和∶

计算每组分量h1（t），h2（t），…，hm（t）的功率谱分布曲线H1（ω），H2（ω），…，Hm（ω）。利用式（21）计算每组分量的谱线在频段［ωp1，ωq1］，…，［ωpk，ωqk］内的幅值累加占全局幅值累加的比值η∶

如果对应分量计算得到的η大于预设门限TH（实验中取值0.5），则该分量作为组成重构信号C1（n）的分量之一，否则将该分量丢弃。

假设符合标准的IMFs分量有z个，则重构信号C1（n）为

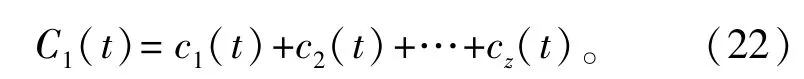
对第二路接收信号y2（n）按照式（20）～（22）进行与y1（n）同样的处理，得到重构信号C2（t）。利用式（1）～（5）二次相关基本模型，计算C1（t）、C2（t）的二次相关序列RRc1c1Rc1c2（τ），对二次相关序列峰值进行检测可得到时延估计^σ∶

4　实验仿真结果与分析

采用时长为2 375 ms，频率范围0～4 000 Hz，采样频率fs=8 000 Hz，N=19 000的纯净语音信号，其语谱图如图2所示。为了对比SC法、GSCC法、Wavelet-SC法与EMD-SC的性能，本文在不同环境下对这些算法进行了仿真，其中噪声取高斯白噪声和非高斯有色噪声，时延Δτ取10 ms、30 ms以及50 ms，信噪比从0 dB变到-24 dB。将加性噪声为高斯白噪声，不同时延和信噪比条件下，各种算法分别进行500次时延估计，得到结果的均方根误差εRMSE见表1。将加性噪声为非高斯有色噪声，时延Δτ为30 ms，不同信噪比条件下，各种算法分别进行500次时延估计，得到结果的εRMSE见表2，为了方便表示，将时延估计的检测结果以采样单位来衡量，并非绝对时间。表1和表2中“×”表示不能估计时延或估计的时延误差很大。

图2　纯语音信号的语谱图Fig.2 Signal spectra of pure speech

表1　高斯白噪声、不同时延和信噪比条件下各算法估计结果的εRMSETab.1 εRMSEof estimation algorithms in the condition of Gaussian noise，different delay and SNR

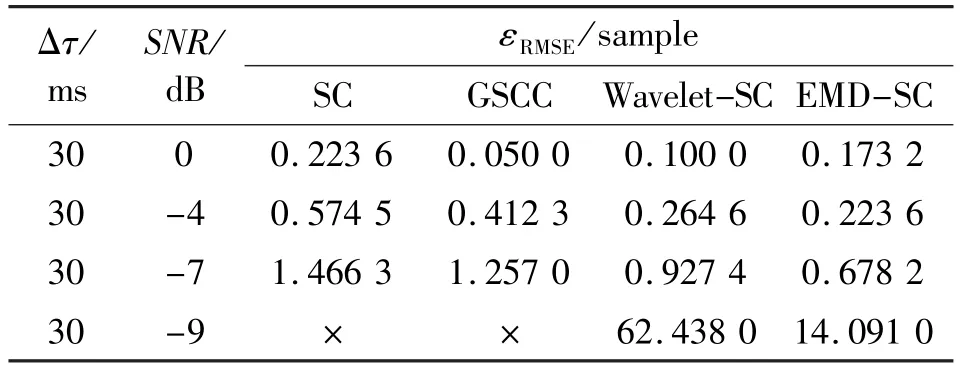
表2　非高斯有色噪声、时延取30 ms、不同信噪比条件下各算法估计结果的εRMSETab.2 εRMSEof estimation algorithms in the condition of colored non-Gaussian noise，30 ms delay and different SNR

从表1可以看出∶在不同时延、低信噪比条件下，GSCC、Wavelet-SC以及EMD-SC法相对于SC方法都能得到更低的时延估计误差，说明这3种方法都改善了SC法的抗噪性能；在信噪比高于-5 dB时，GSCC法相对于Wavelet-SC和EMD-SC法，得到的时延估计误差略低，但是，随着信噪比的降低Wavelet-SC和EMD-SC法抗噪性能的优势逐渐凸显，在信噪比为-17 dB时，Wavelet-SC法和EMDSC法的εRMSE分别为GSCC法的30%和20%，说明Wavelet-SC法与EMD-SC法在信噪比较低的条件下都具有较好的抗噪性能；在信噪比高于-5 dB时，Wavelet-SC法与EMD-SC法的εRMSE相当，但EMDSC方法在信噪比低于-10 dB时，表现得更加稳健，在信噪比为-17 dB不同时延条件下得到的εRMSE还能控制在11个采样以内，说明EMD-SC法相对于Wavelet-SC法在低信噪比情况下性能更优。

从表2可以看出∶在非高斯有色噪声条件下，4种方法的性能都下降了大约7 dB；此外，在信噪比低于-4 dB时，Wavelet-SC法与EMD-SC法的估计误差远低于SC法与GSCC法；在信噪比低于-7 dB时，EMD-SC法相对于Wavelet-SC法抗噪性能提升更加明显。表2在非高斯有色噪声条件下进一步验证了表1的实验结果。

为了有个更直观的认识，本文统计了加性噪声为高斯白噪声，信噪比从0 dB变到-24 dB，时延Δτ取10 ms、30 ms以及50 ms时，各种算法对时延估计结果的均方根误差εRMSE和异常点百分比γanom，并对不同时延得到的εRMSE和γanom做算术平均，得到平均均方根误差¯εRMSE和平均异常点百分比¯γanom在不同信噪比条件下的分布情况如图3和图4所示。

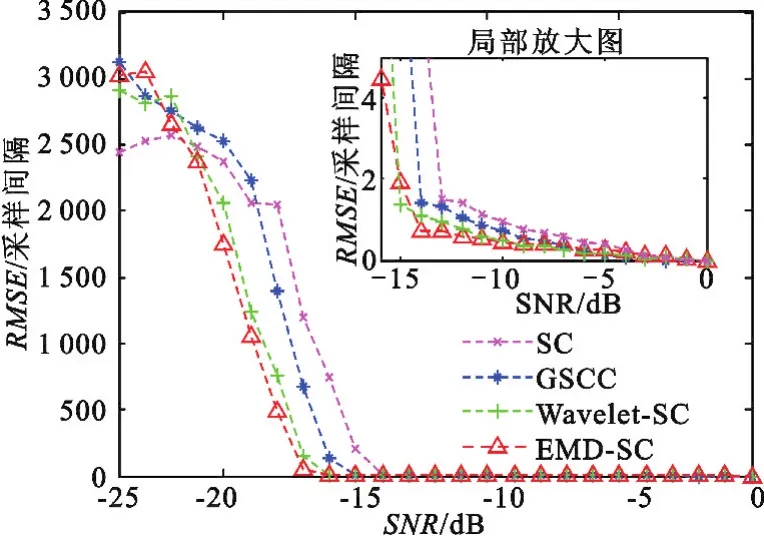
图3　高斯白噪声且不同信噪比条件下的平均RMSE及局部放大图Fig.3 The average RMSE under the condition of white Gaussian noise with different SNR and its local amplification figure

图4　高斯白噪声且不同信噪比条件下的平均异常点百分比Fig.4 The average abnormal percentage points under the condition of white Gaussian noise with different SNR

图3平均了不同时延下4种方法的εRMSE，从图中可直观地看出EMD-SC和Wavelet-SC法与SC和GSCC法相比，在信噪比高于-5 dB时估计误差相差很小，但是，随着信噪比的降低，EMD-SC和Wavelet-SC法估计误差远低于SC和GSCC法。此外，Wavelet-SC法与EMD-SC法的平均RMSE曲线非常接近，从局部放大图可以看出，信噪比低于-10 dB后，EMD-SC法的估计误差略低于Wavelet-SC法，相对性能更优。

由图4可知∶SC法、GSCC法分别在信噪比为-7 dB和-9 dB时开始逐渐出现异常估计点，Wavelet -SC和EMD-SC法在-12 dB时才开始出现异常估计点；并且，EMD-SC法在信噪比低于-10 dB时异常点曲线要低于其余3种方法，说明EMD-SC法在低信噪比情况下得到的估计结果更加稳健、可靠。

下面对实验结果进行分析。在非高斯有色噪声条件下，4种方法低信噪比的时延估计误差大大增加。这是因为非高斯有色噪声和信号之间存在相关性，式（2）和式（3）中Rsn2（τ）、Rsn1（τ）、Rn1s（τ-D）在信噪比较低的情况下不能再假设为零。当信噪比降低到一定程度，噪声与噪声、噪声与信号之间的相关波形的峰值甚至会超过语音信号间的相关序列峰值，导致估计时延出现误判。此外，Wavelet-SC法在低信噪比条件下的估计性能与EMD-SC法相当，但是，由于Wavelet-SC法的小波变换中所用小波不具唯一性，且小波变换中采用不同的小波基分析同一问题会产生不同的结果，导致Wavelet-SC法存在难以选择合适的小波，且无法自适应各种复杂场合的问题。而EMD-SC法中进行EMD变换得到的是自适应广义基，对不同信号进行分解会得到不同的基函数，满足不同场合的自适应条件。综合实验结果的分析，EMD-SC法在其余3种时延估计方法的基础上，进一步提高了低信噪比条件下时延估计的抗噪性能，并且能得到更准确和稳健的时延估计结果。

5　结束语

本文应用EMD方法能够抑制含噪信号中噪声成分的特点，将其应用于低信噪比下的声达时延估计。采用倒谱法分离语音信号中的声门脉冲激励和声道响应，结合谱减法，得到区分含噪信号中有用信号主导频段的方法，从而利用EMD分解后IMFs分量的功率谱特性，提出新的EMD重构分量选择方案。在高斯白噪声和非高斯有色噪声且不同时延条件下，EMD-SC与SC法、GSCC法、Wavelet-SC法相比，都能得到更优的抗噪性能。基于EMD-SC方法能在实验中得到较好的抗噪声能力，接下来可以进一步研究该方法在存在室内反射噪声、混响条件下的性能。

［1］ ALAMEDA-PINEDA X，HORAUD R.A geometric approach to sound source localization from time-delay estimates［J］.IEEE Transctions on Audio，Speech，and Language Processing，2014，22（6）∶1082-1095.

［2］ WU Y Q，SONG H J，XU F.Time delay estimation in underwater positioning for pattern time delay shift coding［J］//Proceedings of 2013 6th International Congress on Image and Signal Processing.Hangzhou∶IEEE，2013∶1618-1622.

［3］ CHOUDHARY H，BAHL R，KUMAR A.Inter-sensor time delay estimation using cepstrum of sum and difference signals in underwater multipath environment［J］. Unerwater Technology，2015，23（2）∶1-7.

［4］ LI P X，HE Y Z，CUI G F，et al.A novel timing advanced estimation algorithm for eliminating frequency offset in satellite system［C］//Proceedings of 2015 IEEE 26th Annual International Symposium on Personal，Indoor，and Mobile Radio Communications（PIMRC）.Hong Kong∶IEEE，2015∶1792-1796.

［5］ ALVAREZ-AGUIRRE A，WOUW N，OGUCHI T，et al.Predictor-based remote tracking control of a mobile robot［J］. Conrol Systems Technology，2014，3（4）∶2087-2102.

［6］ KNAPP C H，CARTER C G.The generalized correlation method for estimation of time delay［J］.IEEE Transactions on Acoustics，Speech and Signal Processing，1976，21（2）∶320-327.

［7］ REED F A，FEINTUCH P L，BERSHAD N J.Time delay estimation using the LMS adaptive filter-behavior［J］. IEEE Transactions on Acoustics，Speech and Signal Processing，1981，29（3）∶561-571.

［8］ 曾小东.LS曲线拟合的时延估计［J］.电讯技术，2015，55（10）∶1176-1181.

ZENG Xiaodong.Time delay estimation by LS curve fitting［J］.Telecommunication Engineering，2015，55（10）∶1176-1181.（in Chinese）

［9］ TANG J，XING H Y.Time delay estimation based on second correlation［J］.Computer Engineering，2007，33（21）∶266-267.（in Chinese）

［10］ 周康辉，董万胜，刘恒毅，等.利用二次相关改进的广义互相关时延估计算法［J］.数据采集与处理，2013，28（6）∶801-805.

ZHOU Kanghui，DONG Wansheng，LIU Hengyi，et al. Improving GCC time delay estimation by second correlation method［J］.Journal of Data Acquisition and Processing，2013，28（6）∶801-805.（in Chinese）

［11］ 殷恒刚.基于小波变换二次相关时延估计算法的声定位技术及试验研究［D］.南京∶南京理工大学，2009.

YIN Henggang.Research of sound location based on wavelet transform and second correlation time delay estimation method［D］.Nanjing∶Nanjing University of Science and Technology，2009.（in Chinese）

［12］ CHEEPURUPALLI K K，KONDURI R R.Robust time delay estimation for noise corrupted sinusoidal signals［C］//Proceedsings of 2013 International Conference on Multimedia，Signal Processing and Communication Technologies.Aligarh，India∶IEEE，2013∶145-149.

［13］ 宋知用.MATLAB在语音信号分析与合成中的应用［M］.北京∶北京航空航天大学出版社，2013.

SONG Zhiyong.The application of MATLAB to speech signal analysis and synthesis［M］.Beijing∶Beijing University of Aeronautics and Astronautics Press，2013.（in Chinese）

［14］ SHARM A，CHAR U，BHARDWA J，et al.Applications and simulation of adaptive filter in noise cancellation［J］.Journal of Information Systems and Communication，2012，3（1）∶334-339.

［15］ DONOHO D L.De-noising by soft thresholding［J］. IEEC Transactions on Information Theory，1995，41（3）∶613-627.

周卓伟（1990—），湖南益阳人，硕士研究生，主要研究方向为语音信号处理、目标定位；

ZHOU Zhuowei was born in Yiyang，Hunan Province，in 1990.Heisnowagraduate student.His research concerns speech signal processing and target location.

Email∶ling_ren@126.com

孙山林（1973—），男，河南邓州人，博士，教授，主要研究领域包括全相位FFT在OFDM系统中的应用、全相位FFT信号处理、光-无线通信系统设计等；

SUN Shanlin was born in Dengzhou，Henan Province，in 1973.He is now a professor with the Ph.D.degree.His research concerns application of all-phase FFT in OFDM system，allphase FFT signal processing and optical-wireless communication system design.

李 云（1978—），女，广西南宁人，博士研究生，主要研究方向为网络信息安全、水下传感网络、认知网络。

LI Yun was born in Nanning，Guangxi Zhuangzu Autonomous Region，in 1978.She is currently working toward the Ph. D.degree.Her research concerns network information security，underwater sensor network and cognitive network.

Second Correlation Time Delay Estimation Based on Empirical Mode Decomposition Reconstruction

ZHOU Zhuowei1，SUN Shanlin2，LI Yun2，CHEN Pangsheng1，SHEN Jingwen2
（1.Institute of Information and Communication，Guilin University of Electronic Technology，Guilin 541004，China；2.College of Electronic Information and Automation，Guilin University of Aerospace Technology，Guilin 541004，China）

∶For the purpose of enhancing anti-noise capability of time delay estimation，a novel method named EMD-SC is proposed by applying Empirical Mode Decomposition（EMD）technique to Second Correlation（SC）method in this paper.In addition，the cepstrum method and the subtraction of frequency spectrum method are used to select the signal-led Intrinsic Mode functions，which are produced by EMD，for signal reconstruction.Comparison of the simulation results between EMD-SC method and traditional Second Correlation method at various signal-to-noise ratio（SNR）levels shows that the proposed method obtains a much sharper second correlation peak，and decreases the SNR of precise estimation by 4 dB and 2 dB in the colored non-Gaussian noise and Gaussian white noise.

∶time delay estimation；empirical mode decomposition；second correlation；sound location

Guangxi Scientific Research and Technical Development Program（Guikegong1598008-29）；Research on Up-coversion Technique for User End of OFDM-based Wireless-optical Network（ZD2014146）

TN971.1

A

1001-893X（2016）05-0562-06

10.3969/j.issn.1001-893x.2016.05.015

周卓伟，孙山林，李云，等.基于经验模态分解重构的二次相关时延估计［J］.电讯技术，2016，56（5）∶562-567.［ZHOU Zhuowei，SUN Shanlin，LI Yun，et al.Second correlation time delay estimation based on empirical mode decomposition reconstruction［J］.Telecommunication Engineering，2016，56（5）∶562-567.］

2015-09-25；

2016-01-04Received date：2015-09-25；Revised date：2016-01-04

广西科学研究与技术开发计划项目（桂科攻1598008-29）；基于OFDM的无线-光网络用户端上变频技术研究（ZD2014146）

**通信作者：shy1997@126.comCorresponding author：shy1997@126.com