一种高安全性的级联型混沌扩频序列*

陈紫强，舒 亮，谢跃雷

（桂林电子科技大学认知无线电与信息处理省部共建教育部重点实验室，广西桂林　541004）

一种高安全性的级联型混沌扩频序列*

陈紫强，舒 亮**，谢跃雷

（桂林电子科技大学认知无线电与信息处理省部共建教育部重点实验室，广西桂林541004）

针对传统一维混沌映射产生序列复杂度低、保密性不理想等问题，提出了一种基于Logistic改进型映射和Cubic映射的级联型混沌序列。新序列的混沌映射表达式由原来的低次一阶差分方程扩展为高次二阶差分方程，映射迭代过程由单级迭代变为二级交叉迭代，从而提高了混沌系统的复杂性。对新序列的非线性动力学混沌特性和扩频通信性能进行了仿真对比，结果表明新序列具有混沌吸引子结构更加复杂、初值敏感性更强、序列复杂度更高、安全性更好的特点，最后验证了新混沌序列具有和传统一维混沌序列相当的扩频特性。

扩频通信；混沌序列；Logistic改进型映射；Cubic映射

1　引　言

目前，扩频通信系统的优势主要体现在抗干扰性和保密性［1］，在军事通信、远程导航和水声通信等领域使用广泛，其中直接序列扩频通信在目前的通信系统中使用最为普遍。在直接扩频系统中，最重要的就是要选择合适的扩频码序列。基于线性反馈移位寄存器产生的传统伪随机序列由于存在数目有限、复杂度低、保密性差等缺点已不能满足如今直扩系统容量大、多址干扰小等要求［2］，因而研究新的扩频码序列已经成为现阶段该领域的重要研究内容，其中混沌扩频码目前已成为一种新型的扩频序列。

混沌系统由于其产生的序列具有良好的类随机性、非周期性和非线性、类白噪声统计特性等特点，使得混沌系统具有相当强的抗干扰能力。目前，扩频通信系统中常用Logistic型及其Logistic改进型［3］、Chebyshev型［4］和Cubic型［5］等传统单一的混沌映射所产生的混沌序列作为扩频码序列。这些单一混沌扩频序列虽然生成算法简单，使用起来方便，可以作为扩频码运用于直扩通信系统中，但是存在复杂度低、保密性差等缺点，尤其是在军用通信系统或者其他对保密性要求较高的通信中，复杂性差的序列容易被破解，因此如何提高和改善混沌扩频序列的复杂性，成为近些年来该研究领域的焦点。文献［6］在传统映射的基础上提出了一种级联型的混沌映射，在提高混沌序列复杂度的同时还改善了混沌序列被截断带来的影响。文献［7］在Logistic混沌映射的基础上进行改进，提出了二级分段Logistic混沌映射的概念，在某种程度上解决了Logistic及其改进型序列复杂度不高、随机性差等问题。

鉴于此，本文提出一种级联结构的混沌映射，通过将Logistic改进型和Cubic两种传统一维混沌映射采用差分相乘形式级联，使混沌映射函数变得更复杂；接着，对新序列与组成它的原始序列以及文献［7］所提出的分段Logistic序列的混沌特性进行对比仿真研究；最后将新型序列作为扩频码在扩频系统中进行误码率仿真分析，验证新序列作为扩频系统中的扩频码的可行性。

2　新型混沌序列产生方法

2.1传统一维混沌映射

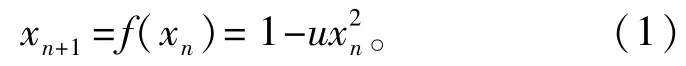
Logistic改进型映射的表达式为式中∶μ的取值范围为［0，2］。在-1＜xn＜1时，该映射是否处于混沌状态取决于参数μ的取值，其产生序列的倍周期分岔［8］如图1（a）所示，由图可知在μ取值区间为［1.4，2］时，该序列处于混沌状态。

Cubic映射的表达式为

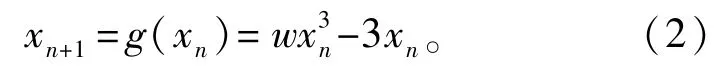
式中∶参数ω的取值范围为（4，6）。当-1＜xn＜1时，则此时该映射处在混沌状态，其混沌映射所对应序列的倍周期分岔图如图1（b）所示，由图可以看出Cubic序列在中间带状区域上处于混沌状态。

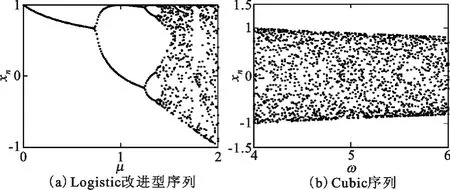
图1　混沌序列分岔图Fig.1 The bifurcation diagram of chaotic sequence

从图1（a）可以看出在Logistic改进型映射中当且仅当μ=2时处于满映射状态［9］，很明显，在满映射状态下，序列的随机取值可以从-1取到1，序列取值非常灵活，这对于通信的保密和信息安全非常重要；而在非满映射状态下，序列不能取到所有值，甚至产生的值域集中分布在一段狭窄的范围，在保密扩频通信或者其他对信息安全要求高的通信中，将增大第三方破解该序列的可能性，因而非满映射尤不适用对保密性要求高的通信系统中。图1（b）的满映射状态只在当ω=4时可以取到，在其他区间上均不能达到满映射，因此也不利于保密通信，而文献［7］所提出的分段Logistic混沌是在Logistic改进型混沌序列基础上进行了分段处理，其满映射区间范围相对于Logistic改进型混沌有了较大的提高，但还不够理想。

2.2Logistic和Cubic级联型混沌映射

以简单的一维混沌映射为基础，本文提出了Logistic和Cubic的级联型映射的混沌序列，该新型映射可以有如下两种表述方法∶

式中∶f（n）和g（n）是两种均值为零的一维混沌映射。选取前文所介绍的两种映射作为原始映射，按照表达式（3）和表达式（4）的结构构造出新的复合映射分别如式（5）和式（6）所示∶

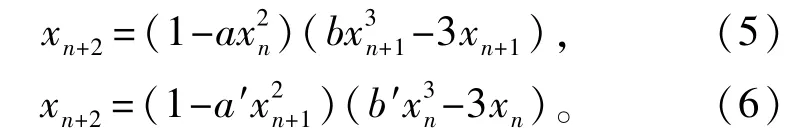
式中∶a∈［1.4，2］；b∈（4，6）。由表达式可以看出，新的复合映射通过将Logistic改进型映射和Cubic映射进行差分相乘级联，使得新产生的混沌映射表达式的最高次是Logistic和Cubic两种原始序列最高次的累加，差分方程由单阶变为二阶，相应的多项式展开之后项数比原始序列更多，由两项增加到四项，由此提高了混沌系统的复杂性。为方便研究，称表达式（5）产生的序列为Logistic-Cubic序列，表达式（6）产生的序列为Cubic-Logistic序列。由于表达式（5）和（6）的结构一样，因此序列的许多性质都一样，只是产生的序列不同，为避免重复研究，本文主要针对Logistic-Cubic序列进行研究，Cubic-Logistic序列只做部分研究。

3　新型混沌序列非线性动力学特性分析

3.1分岔图

图2为式（5）的三维分岔图，其表述了混沌控制参数a和b与序列xn的关系。由图可知，在a∈［1.4，2］、b∈（4，6）的参数范围内几乎都存在混沌行为，而且都是满映射状态。

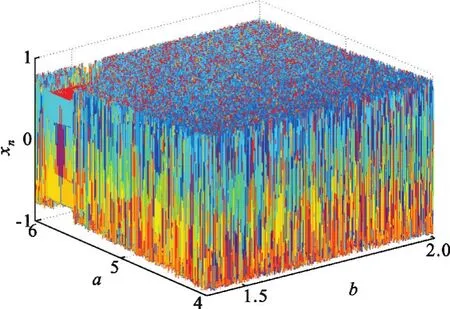
图2　Logistic-Cubic序列三维分岔图Fig.2 The 3-dimensional bifurcation diagram of Logistic-Cubic sequence

图3为Logistic-Cubic序列三维分岔图在a=4和b=2时的截面，对比图3和图1以及文献［7］中分段Logistic映射的混沌倍周期分岔图可以看出，新产生的Logistic-Cubic映射在很大的参数范围内都取得满映射，并且满映射范围多于图1和文献［7］所提出的分段Logistic映射产生的满映射范围，因此Logistic-Cubic映射混沌取值更灵活。

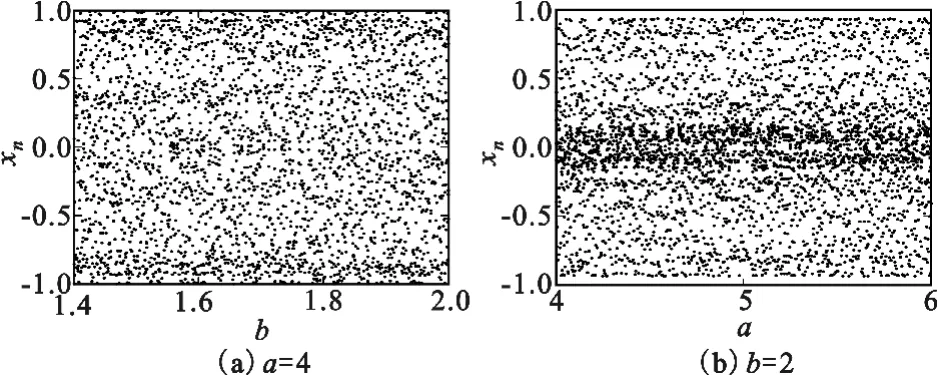
图3　Logistic-Cubic混沌序列分岔图截面Fig.3 The section bifurcation diagram of Logistic-Cubic sequence

3.2混沌吸引子

混沌吸引子又称奇异吸引子，它是无限层条带经过伸长和折叠的几何图像，表示系统的状态随时间呈无规则的非周期状态。混沌吸引子具有混沌的一切特征，包括对初始条件的敏感性、非整数的维数、无穷嵌套的自相似结构，同时也是混沌序列在相空间取值的一个集合。混沌的动力学特征可以通过吸引子的结构和复杂程度来体现，吸引子越复杂，其对应的混沌的动力学特性就越强。本文对多种混沌的三维空间吸引子进行了仿真，结果如图4所示。

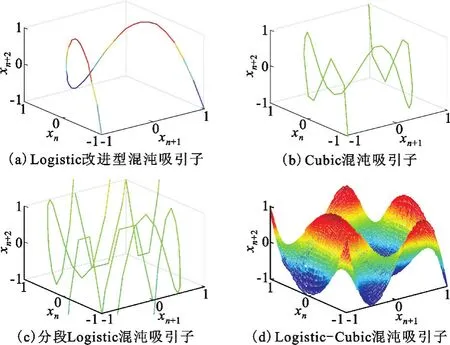
图4　混沌序列三维吸引子Fig.4 The 3-dimensional attractors of chaotic sequence

由图4可以看出，Logistic混沌吸引子和Cubic混沌吸引子分别为三维空间中的抛物线和三次曲线，文献［7］所提出的分段Logistic混沌由于对Logistic改进型混沌映函数进行了分段化处理，其吸引子在三维表现为4条独立的具有相似结构的抛物线。以上3种混沌序列由于序列在迭代出新值时只由前一个迭代值决定，在相空间的迭代轨迹取值只是一条或者多条空间曲线，而Logistic-Cubic映射迭代产生新的混沌值时由两个迭代值决定，因此产生新混沌值的范围更大，吸引子在三维空间中呈现出曲面形式；Cubic-Logistic混沌由于映射表达式和Logistic-Cubic相似，只是取值的先后顺序有区别，在迭代无穷次以后，其呈现出来的吸引子形状与Logistic-Cubic混沌一样。

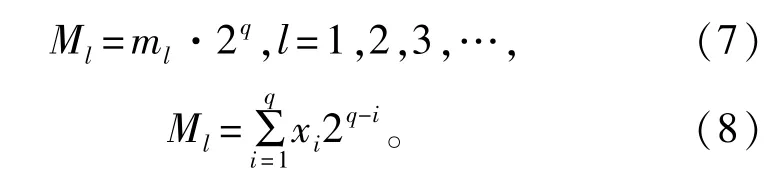
4　Logistic-Cubic混沌序列特性研究

4.1初值敏感性

初值敏感性是指混沌对于初始值具有非常强的依赖性，给定初始值一个微弱的变化，在数次迭代运动过后其产生的轨迹状态和变化之前的轨迹将完全不相干。

现研究Logistic-Cubic序列的初值敏感性。由于Logistic-Cubic序列存在两个初始值x（1）和x（2），因此考虑两种情况，分别对第1个初始值和第2个初始值做微小的改变，如图5所示，a=1.6，b=4，经过50次迭代。其中图5（a）序列的两组初始值为［0.6，0.2］和［0.600 000 1，0.2］，图5（b）序列的两组初始值为［0.6，0.2］和［0.6，0.200 000 1］。

图5　Logistic-Cubic序列时初值敏感性Fig.5 The initial sensitivity of Logistic-Cubic sequence

两个初始值分别为x（1）=0.6和x（2）=0.2，初值改变量均为0.000 000 1，由图可以看出无论哪个初始值发生细微变化，在迭代十几次之后Logistic -Cubic序列的轨迹开始出现无规律的变化，说明Logistic-Cubic序列两个初值的敏感性都很好，相比于一般的一维混沌序列只含有单个初始值的情况，Logistic-Cubic序列多了一个初始值，从而初值敏感性更加灵活多变，序列安全性和保密性更强。序列初值敏感性也可以用Lyapunov指数大小来衡量，它表示系统在相空间相邻轨道的收敛或发散程度。对于一维系统Lyapunov指数可以用映射函数f（x）在n时刻xn的导数来计算［11］。只有当Lyapunov指数大于0时，系统才会出现混沌现象，且指数越大，混沌特性越强，同时也表征系统对初始值的敏感性更好。图6和图7为对Logistic-Cubic序列的Lyapunov指数仿真结果，从图中可以看出，Logistic改进型和Cubic序列级联后，Lyapunov指数在参数范围内均大于0，并且对应参数范围内均高于级联之前的原始序列，这充分说明Logistic-Cubic序列的初值敏感性更好。

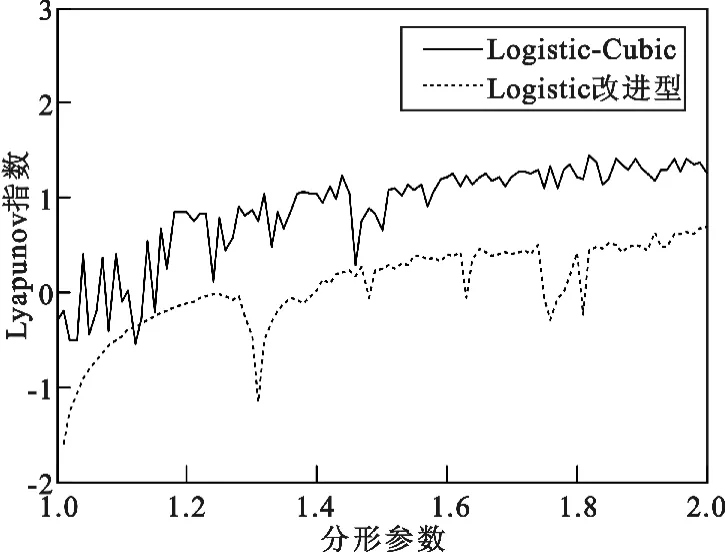
图6　Logistic-Cubic序列（b=6）和Logistic改进型序列Lyapunov指数Fig.6 The Lyapunov exponent of Logistic-Cubic（b=6）and the improved Logistic sequence

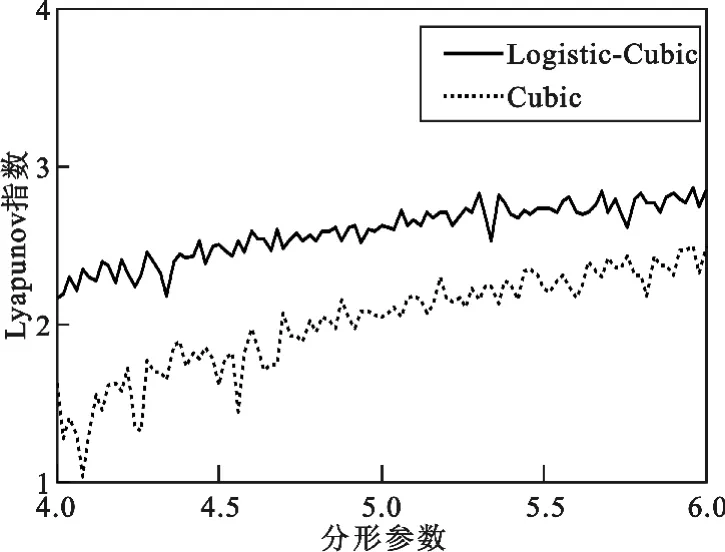
图7　Logistic-Cubic（a=2）和Cubic序列Lyapunov指数Fig.7 The Lyapunov exponent of Logistic-Cubic（a=2）and the Cubic sequence

4.2相关性

为了满足扩频通信要求，混沌序列需要选择相关性良好的序列。对于自相关函数，要求具有尖峰脉冲，而互相关函数则要求其所有函数值尽量接近于零，这样才能够保证系统具有足够的的抗多径干扰和抗多址干扰能力，从而提高数据在传输过程中的可靠性。

混沌序列在理想条件下是非周期的，但由于计算机处理数据精度的影响，在实际使用扩频码序列时要对混沌序列按照需要进行截短。截短后长度为N的序列的自相关函数以及互相关函数如式（9）和式（10）所示∶

式中∶m为序列的相关间隔；N为序列长度。取初始值x（1）=0.72，x（2）=0.23，序列长度N=2 000，相关间隔m=2 000，Logistic-Cubic序列自相关函数结果如图8所示。

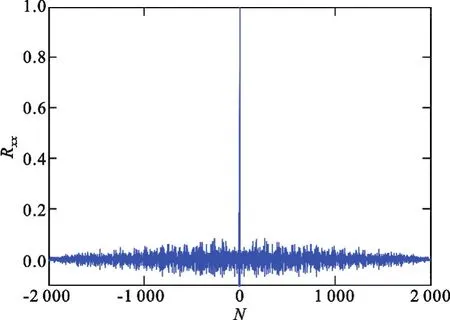
图8　Logistic-Cubic序列的自相关函数Fig.8 The autocorrelation of Logistic-Cubic sequence

选取两对初始值y（1）=0.72，y（2）=0.23以及z（1）=0.72，z（2）=0.230 000 1。序列长度N=2 000，相关间隔为2 000，其互相关曲线如图9所示。

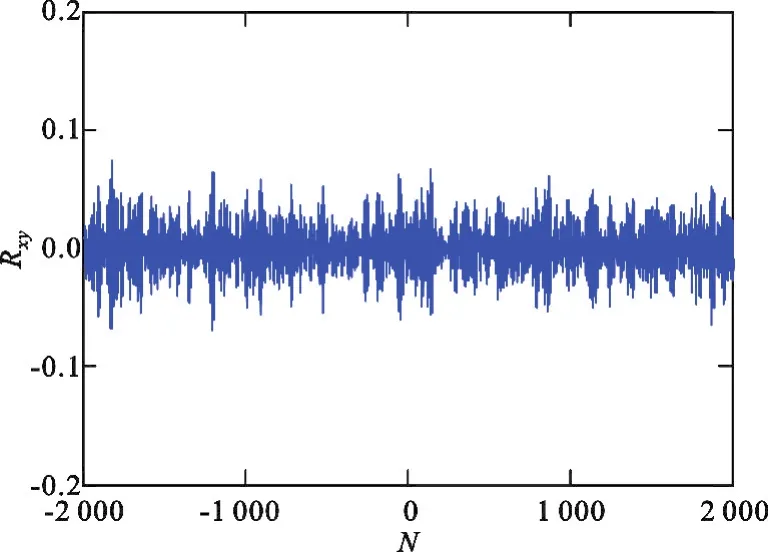
图9　Logistic-Cubic序列的互相关函数Fig.9 The crosscorrelation of Logistic-Cubic sequence

观察图8发现，Logistic-Cubic混沌序列的自相关函数在相关间隔为0时有尖锐的峰值，而在其他相关间隔的值趋近于0，类似于δ函数，自相关性能很好。在图9中，其互相关绝对值主要分布在（0，0.05）之间，互相关值非常小，因此Logistic-Cubic序列的相关性能够满足扩频通信的要求。

4.3混沌序列复杂度分析

复杂度目前在数学上还没有严格定义，在研究混沌序列的复杂度时，一般将定量描述混沌性质的一些参数列入复杂度度量方法。文献［12］提出了采用混沌运动产生的信息量大小，即近似熵（Approximate Entropy，ApEn）来衡量复杂度大小的准则，理论和实践均表明该方法能够简单有效地判断混沌伪随机序列复杂度。

在计算近似熵时一般只需要比较短的数据就能估计出比较稳定的统计值，一般取1 000左右。其判断依据为近似熵值越大，序列的复杂性越大，混沌运动信号的不规则性和随机性也越强。本文采用文献［12］所述的方法对新序列的近似熵进行计算，用它来进行混沌序列复杂度。表1为各种伪随机序列在长度为N时取50个初始值的近似熵平均值。

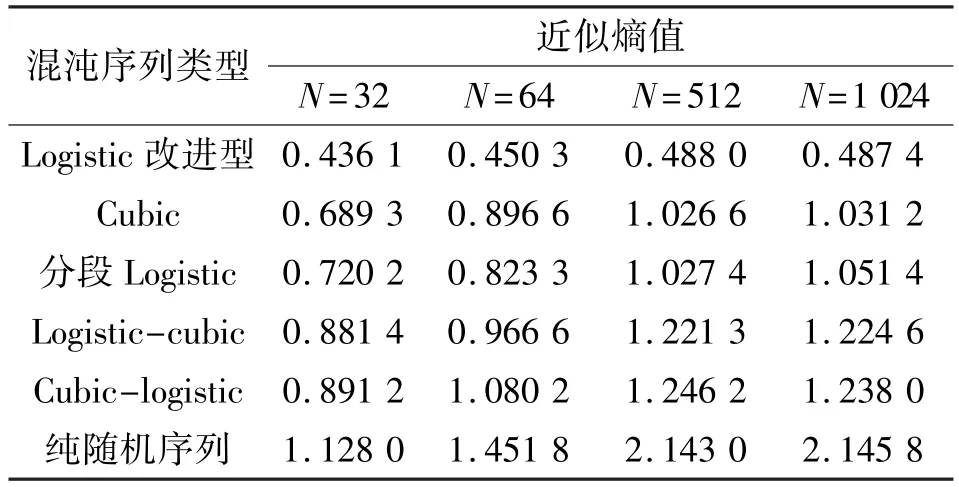
表1　混沌序列近似熵值比较Tab.1 The comparison of approximate entropy value with different chaotic sequence

从表1中可以看出∶本文所提出的Logistic-Cubic序列的复杂性要强于原始序列Logistic改进型和Cubic序列，文献［7］提出的分段Logistic序列由于对Logistic改进型映射表达式进行了分段处理使得序列的复杂性有了一定的提高，但复杂性还是略低于Logistic-Cubic序列；Cubic-Logistic序列由于和Logistic-Cubic序列的相空间吸引子相同，序列复杂性程度相差很小，从数据对比也可以看出来。为了方便对比，本文也给出了（-1，1）区间的纯随机序列的近似熵分析，纯随机序列由于序列是随机产生，序列之间毫无规律，因此序列的近似熵值最高。同时从表中可以看出随着序列长度的增加，序列的近似熵也呈现出上升的趋势；同时还可以看出在序列长度比较短时近似熵还不够稳定，当序列长度取512和1 024的值非常接近，近似熵值很稳定，因此此时的取值基本可以反映出该混沌序列的复杂程度。

5　扩频通信性能仿真

为了验证Logistic-Cubic映射产生的序列作为直接序列扩频系统中的扩频码是否可行，对其进行瑞利衰落信道下的扩频通信性能仿真。系统采用BPSK调制解调，扩频增益取1 000，分别将优选后的Logistic改进型、Cubic和Logistic-Cubic 3种映射生成的实值序列进行抽取q比特量化后作为该系统的扩频码在调制端来调制信息，在解调端再用相同的扩频码解扩，得到3种序列的平均误码率曲线如图10所示。

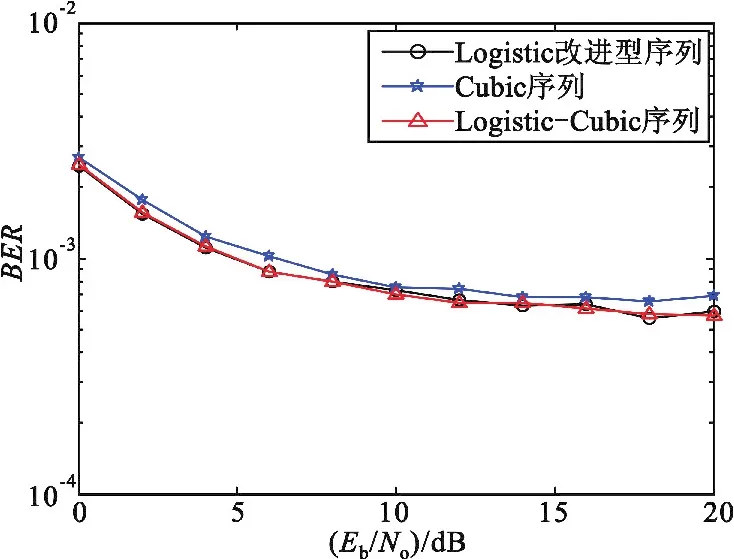
图10　序列的误码率曲线Fig.10 The BER curves of chaotic sequences

由图10可知Logistic-Cubic序列和传统Logistic改进型序列以及Cubic序列的误码性能相当，但Logistic-Cubic序列的安全性和保密性比传统的改进型Logistic序列和Cubic序列更好，因此Logistic-Cubic能够更好地适用于保密通信等对信号安全性要求高的军用领域。

6　结束语

本文提出了一种高安全性的混沌序列，通过将Logistic改进型和Cubic两种传统一维混沌映射进行差分相乘级联，从而改变了混沌系统的迭代过程，并提高了混沌序列的复杂度。研究发现该序列具有比原始序列以及文献［7］所提出的分段Logistic更加复杂的非线性动力学特性和更强的初值敏感性，并且由该混沌映射系统产生的序列的复杂性更高，随机性更强，同时新序列满映射范围更大，产生混沌

的数目更多，并且具有和传统单阶混沌序列相当的误码性能，使得该类型序列在混沌保密扩频通信和对通信安全性高的军事领域可以得到更广泛的应用。本文对于该序列的研究还仅仅处于最基础阶段，为了充分发掘该序列的理论及实用价值，还需进行更加深入的研究。

［1］ DIXON R C.扩展频谱系统［M］.王守仁，项海格，迟惠生，等，译.北京∶国防工业出版社，1982.

DIXON R C.Spread spectrum system［M］.Translated by WANG Shouren，XIANG Haige，CHI Huisheng，et al.Beijing∶National Defense Industry Press，1982.（in Chinese）

［2］ WANG F，HUANG Z T，ZHOU Y.A new method for msequence and gold-sequence generator polynomial estimation［C］//Proceedings of 2007 International Symposium on Microwave，Antenna，Propagation and EMC Technologies for Wireless Communications.Hangzhou∶IEEE，2007∶1039-1044.

［3］ 梁由勇，王涌，赵东风，等.改进型Logistic映射保密通信的仿真研究［J］.实验科学与技术，2013，11（3）∶25-28.

LIANG Youyong，WANG Yong，ZHAO Dongfeng，et al. Simulation of modified Logistic mapping secure communication［J］.Experiment Science and Technology，2013，11（3）∶25-28.（in Chinese）

［4］ GUAN L，LI Z，SI J，et al.Generation and characteristics analysis of cognitive-based high-performance wide-gap FH sequences［J］.IEEE Transactions on Vehicular Technology，2015，64（11）∶5056-5069.

［5］ 于佳.Cubic混沌映射及其在混沌掩盖通信中的应用［D］.长春∶吉林大学，2007.

YU Jia.Cubic chaotic map and its chaotic masking communication application［D］.Changchun∶Jilin University，2007.（in Chinese）

［6］ 潘辉，何世彪.一种新型的适用于CDMA扩频系统的混沌序列［J］.电讯技术，2008，48（4）∶61-64.

PAN Hui，HE Shibiao.a novel spread spectrum sequence suitable for chaotic CDMA system［J］Telecommunication Engineering，2008，48（4）∶61-64.（in Chinese）

［7］ 张薇，谢红梅，王保平.一种新型的分段Logistic混沌扩频通信算法［J］.计算机科学，2013，40（1）∶59-62.

ZHANG Wei，XIE Hongmei，WANG Baoping.A new segment Logistic chaotic spread spectrum communication algorithm［J］.Computer Science，2013，40（1）∶59-62.（in Chinese）

［8］ 侯东晓，赵红旭，刘彬.一类含Mathieu-Duffing振子的相对转动系统的分岔和混沌［J］.物理学报，2013，62（23）∶234501-234501.

HOU Dongxiao，ZHAO Hongxu，LIU Bin.Bifurcation and chaos of a class of Mathieu-Duffing oscillator relative rotation system［J］.Journal of Physics，2013，62（23）∶234501-234501.（in Chinese）

［9］ 余金峰，杨文革，路伟涛，等.满映射Logistic数字混沌序列的产生及性能分析［J］.电讯技术，2013，53（2）∶140-145.

YU Jinfeng，YANG Wenge，LU Weitao，et al.Production and performance analysis of full digital mapping Logistic chaotic sequence［J］.Telecommunication Engineering，2013，53（2）∶140-145.（in Chinese）

［10］ 柳平，闫川，黄显高.改进的基于Logistic映射混沌扩频序列的产生方法［J］.通信学报，2007，28（2）∶134-140.

LIU Ping，YAN Chuan，HUANG Xiangao.Improved generation method based on Logistic map chaotic sequence spread spectrum［J］.Journal on Communications，2007，28（2）∶134-140.（in Chinese）

［11］ 赖建文，周世平，李国辉，等.非重正交的李雅普诺夫指数谱的计算方法［J］.物理学报，2000，49（12）∶2328-2332.

LAI Jianwen，ZHOU Shiping，LI Guohui，et al.Calculation of non-orthogonal weight Lyapunov exponent spectrum［J］Journal of Physics，2000，49（12）∶2328-2332.（in Chinese）

［12］ 王云雄，翁贻方，郑德玲.混沌的复杂度研究方法和Logistic映射分析［J］.北京工商大学学报（自然科学版），2006，24（2）∶38-41.

WANG Yuxiong，WENG Yifang，ZHENG Deling.Chaotic complexity of research methods and Logistic mapping analysis［J］.Beijing Technology and Business University（Natural Science Edition），2006，24（2）∶38-41.（in Chinese）

陈紫强（1973—），男，湖南益阳人，副教授、硕士生导师，主要研究方向为信道编码、协作通信；

CHEN Ziqiang was born in Yiyang，Hunan Province，in 1976.He is now an associate professorandalsotheinstructorofgraduate students.His research concerns channel coding and cooperative communication.

Email∶chenziqiang@guet.edu.cn

舒 亮（1989—），男，湖南醴陵人，硕士研究生，主要研究方向为扩频通信和水声通信；

SHU Liang was born in Liling，Hunan Province，in 1989.He is now a graduate student.His research concerns spread spectrum communication and underwater acoustic communication.

Email∶593778730@qq.com.

谢跃雷（1975—），男，河北邯郸人，副教授、硕士生导师，主要研究方向为通信信号处理和阵列信号处理。

XIE Yuelei was born in Handan，Hebei Province，in 1975. He is now an associate professor and also the instructor of graduate students.His research concerns communication signal processing and array signal processing.

A High Security Serial Chaotic Spread Spectrum Sequence

CHEN Ziqiang，SHU Liang，XIE Yuelei
（The Ministry of Education Key Laboratory of Cognitive Radio and Information Processing，Guilin University of Electronic Technology，Guilin 541004，China）

∶The sequence generated by the traditional single chaotic map has the problem of low complexity and poor secrecy.This paper proposes a serial chaotic sequence based on improved Logistic mapping and Cubic mapping.The expression of chaotic mapping by the original low times first order difference equations expands to high times second order difference equation，and mapping iterative process is changed from single-stage iteration to second-stage cross iteration so that the new sequence produces a more complex mapping expression of chaos.The nonlinear dynamics chaos characteristics and spread spectrum communication performance of the new sequence are simulated and the results show that the attractors of the proposed chaotic sequence are more complex，the initial sensitivity is more stronger.The complexity of this sequence becomes higher.This sequence possesses much better security performance.Finally the feasibility of the chaotic sequence in spread spectrum communication is verified.

∶spread spectrum communication；chaotic sequence；improved Logistic mapping；Cubic mapping

The National Natural Science Foundation of China（No.41201479）；The Natural Science Foundation of Guangxi（2014jjAA70068）；Key Project of Guangxi Education Department（ZD2014052）

TN911.7

A

1001-893X（2016）05-0476-07

10.3969/j.issn.1001-893x.2016.05.002

陈紫强，舒亮，谢跃雷.一种高安全性的级联型混沌扩频序列［J］.电讯技术，2016，56（5）∶476-482.［CHEN Ziqiang，SHU Liang，XIE Yuelei.A high security serial chaotic spread spectrum sequence［J］.Telecommunication Engineering，2016，56（5）∶476-482.］

2016-01-19；

2016-04-25Received date：2016-01-19；Revised date：2016-04-25

国家自然科学基金资助项目（41201479）；广西自然科学基金资助项目（2014jjAA70068）；广西教育厅重点项目（ZD2014052）

**通信作者：593778730@qq.comCorresponding author：593778730@qq.com