以非负矩阵分解提取局部特征的SAR目标稀疏表示分类*

张之光，雷 宏

（中国科学院电子学研究所，北京　100190）

以非负矩阵分解提取局部特征的SAR目标稀疏表示分类*

张之光**，雷 宏

（中国科学院电子学研究所，北京100190）

合成孔径雷达（SAR）目标分类是自动目标识别系统的核心功能之一，对于战场监视等应用具有重要意义。利用SAR图像局部散射明显的特点，提出了通过训练样本的非负矩阵分解获得低维数局部特征编码，并以该编码作为字典进行稀疏表示分类的方法。采用Gotcha项目民用车辆目标的实测数据进行了验证，结果显示在不同信噪比条件下该方法的分类正确率均优于广泛采用的由降采样、随机投影、主成分分析提取低维数特征的稀疏表示分类方法，表明了该方法的性能优势。另外，还通过实验对比分析了非负约束的稀疏表示与标准稀疏表示在分类性能上的差别，结果显示非负约束的稀疏表示导致分类正确率下降，故针对分类问题不宜在稀疏表示时进行非负约束。

合成孔径雷达；稀疏表示；目标分类；非负矩阵分解；局部特征提取

1　引　言

合成孔径雷达（Synthetic Aperture Radar，SAR）是一种主动微波成像系统，具有全天时、全天候的地物成像能力。SAR目标分类指的是根据已知类别的目标图像集合，将获取的未知类别目标图像进行归类，即判断其属于哪个目标。已知类别的目标图像称为训练样本，待归类的未知类别目标图像称为测试样本。

近年来，稀疏表示的求解及应用成为计算机视觉、信号处理、模式识别等领域的研究热点［1］。稀疏表示的核心是求解y=Ax欠定方程，该方程中观测向量y已知，字典A已知或可以通过学习得到，向量x未知。稀疏表示的目标是获取x的最小0范数（即非零元素个数）解，通常将0范数约束凸松弛为1范数约束以便于求解。

Wright等［2］首先将稀疏表示用于人脸光学图像识别，提出稀疏表示分类（Sparse Representation Classification，SRC）方法，通过求取测试样本y在训练样本集合所建字典A下的稀疏表示系数x，根据x各元素大小、密集程度来判断目标类别。相较于最近邻域、最近子空间等传统分类方法，稀疏表示分类在不同光照下的人脸识别问题中取得了更高的识别率。y与A一般先进行降维处理，以保证y=Ax欠定，使其满足稀疏求解的条件，与此同时降维可大幅减少运算量。

SRC很快被引入SAR目标分类领域，与最近邻、最近子空间等传统分类方法相比取得了更好的结果［3］。文献［4］用圆迹SAR各方位角的图像作为训练样本，采用主成分分析（Principle Components A-nalysis，PCA）降维，对降维后的数据进行稀疏表示分类。文献［5］根据舰船SAR图像的特点，用图像质心、图像协方差、局部雷达截面密度等一系列参数构造特征，基于该组特征将图像样本以低维向量编码，对编码进行稀疏表示分类。该方法的优点是特征的描述性很强，样本可以大幅度降维；缺点是提取的特征针对舰船目标，通用性差。文献［6］指出“去除稀疏表示解中与输入信号呈负相关的原子更加符合SAR目标识别应用”，以随机投影方法对数据进行降维后，在采用稀疏表示分类时对稀疏表示系数进行了非负约束，称为非负稀疏表示分类（Nonnegative SRC，NSRC）。

SAR图像的特点是局部特征明显，图像可由局部特征加性组合构成。因此，适于提取局部特征的非负矩阵分解（Non-negative Matrix Factorization，NMF）在SAR图像特征提取方面得到应用。然而现有文献将NMF提取出的特征用于配合线性判别［7］、支持向量机［8］等传统分类方法进行目标分类，而文献［2］已验证稀疏表示分类的性能优于线性判别及支持向量机。

综上所述，当前应用于SAR目标分类的SRC类方法在降维时均未考虑SAR图像的普遍特点；NMF特征提取利用了一般SAR图像的特点，然而当前结合NMF进行分类的研究在分类步骤中尚无采用SRC方法。因此，有必要结合现有SRC与NMF方面的研究探索进一步提高SAR目标分类正确率、增强分类方法在不同信噪比条件下的适用性的新方法。

本文提出首先对原始训练样本集合进行非负矩阵分解，获得特征矩阵与编码矩阵，然后以低维数的编码矩阵代替原始训练样本进行稀疏表示分类（记作NMF+SRC）的方法。基于SAR实测数据将本文方法与常用的采用降采样、随机投影、主成分分析进行降维的稀疏表示分类方法进行了对比，实验结果表明在不同的信噪比条件下NMF+SRC比其他“降维+SRC”方法均获得了更高的分类正确率；另外，对比了SRC与文献［6］提出的NSRC性能上的差别，结果表明SRC比NSRC更适于SAR目标分类。

2　NMF+SRC原理

2.1非负矩阵分解

有别于主成分分析（PCA）等获取全局特征的方法，非负矩阵分解（NMF）是获取局部特征的有效方法。NMF从训练样本图像集合中提取出特征图像，使得每一幅训练样本图像都能够用特征图像的非负线性组合来近似表示。从矩阵分解的角度来分析，NMF可以用公式（1）或逐元素形式的公式（2）来表示∶

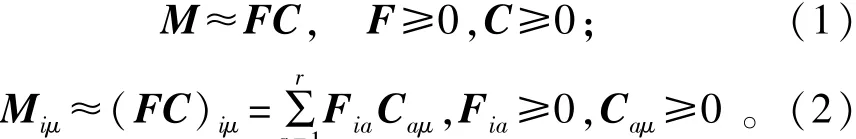
将每一幅像素数目为m的训练样本图像拉直为列向量，排列n个列向量构成矩阵M。训练样本图像的像素值非负，因此M非负。

特征矩阵F包含r列，每一列是一幅向量形式的非负特征图像。编码矩阵C的每一列是基于F的编码，与M中相应列位置的训练样本图像一一对应。特征矩阵F与编码矩阵C的尺寸分别为m×r和r×n。NMF采用公式（3）所示的迭代算法［9］求解∶

式中∶i、μ指示矩阵元素位置。

NMF的特别之处在于对F和C采用非负约束，它只允许对非负特征进行加法操作以近似原始图像，这与由部分组成整体的直观认知相符，正是非负约束实现了基于局部特征的表示。图1示意了由NMF特征与PCA特征分别表达车辆目标SAR图像的区别（仅列出部分特征）。可以看到NMF特征表现出明显的局部性，通过线性组合表达原始图像时系数全为正值；而PCA特征表现出明显的全局性，线性组合系数含负值。与光学图像不同，SAR图像本身由局部的散射中心构成，由少量NMF特征的加性组合即可有效描述。

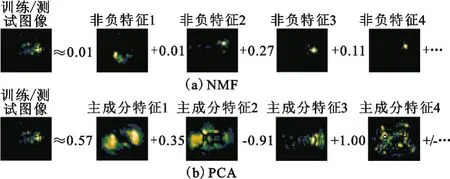
图1　由特征图像的线性组合表达原始SAR图像Fig.1 Representation of an original SAR image by linear combinations of feature images

2.2稀疏表示分类

第i个目标的训练样本集合为Mi∶

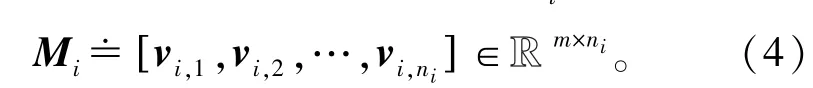
式中∶vi，ni为第i个目标的第ni个训练样本，为二维图像拉直后的向量。用全部k个目标的训练样本集合构造字典M∶

通过求解方程（6）得到测试样本v在字典M下的稀疏表示系数向量x，然后根据x中系数最大值的位置或者系数最密集的位置来确定测试样本v的类别［2］。

实际中为了保证方程欠定以求得稀疏解，一般还需要对字典和测试样本进行一致的降维操作，降维操作使得求解方程（6）的运算量显著降低。

2.3NMF+SRC流程

本文提出的NMF+SRC方法将训练样本集合分解为非负特征矩阵与编码矩阵，以低维数的编码矩阵代表训练样本作为字典，对测试样本的编码向量进行稀疏表示。完整流程包括以下4个步骤∶

（1）对训练样本集合M进行非负矩阵分解，得到特征矩阵F与编码矩阵C；

（2）将测试样本v基于特征矩阵F进行编码，求取编码向量c的非负最小二乘解；

（3）以编码矩阵C为字典将测试样本的编码向量c进行稀疏表示；

（4）根据稀疏表示系数向量x中系数最大值位置或最密集位置判决目标类别。

流程中的前3个步骤如图2所示。因稀疏表示采用的字典C非负，所以步骤2要求对c进行非负约束，以使得稀疏表示的观测向量与字典性质相同［1］，该步骤由公式（7）描述∶

步骤3的稀疏表示见公式（8），以Homotopy［10］算法求解∶

图2　NMF+SRC方法流程图Fig.2 NMF+SRC method flowchart

3　实验验证

3.1实验设置

实验数据来自Gotcha项目［11］圆迹SAR的原始相位历程，使用BP算法［12］处理每4°方位角合成孔径数据以获得一幅图像，各合成孔径在方位向上相差1°，因此对于每个航迹，共获得360幅图像。

截取场景中轿车、旅行车、叉车的目标图像进行三目标分类实验，场景与目标的图像分别如图3和图4所示。以航迹1获得的目标图像集合作为训练样本，从另一飞行高度的航迹8所得全部目标图像中每次挑出一幅作为测试样本。航迹1与航迹8的仰角相差约1°（45°与43.8°@90°方位角），不存在与测试样本完全相同的训练样本。

图3　Gotcha场景SAR图像及圈出的3个车辆目标Fig.3 SAR image of Gotcha scene along with three marked vehicle targets

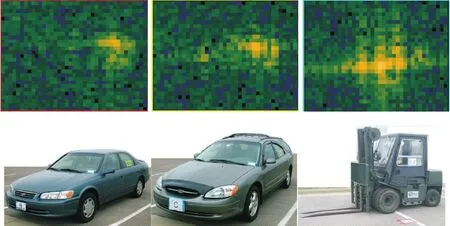
图4　轿车、旅行车、叉车的SAR图像样本与对应的光学图像Fig.4 SAR image samples of Saloon，Wagon，and Lifter with corresponding photos

每幅目标图像的分辨率为30 pixel×40 pixel，拉直后变为1 200维的向量。将航迹1获得不同方位角的轿车图像360幅、旅行车图像及叉车图像各360幅逐个拉直后拼成大矩阵M，则M的行数目为1 200，列数目为1 080，如果直接代入式（6）则不满足方程欠定条件，必须降维后才能用稀疏表示求解。以同样方法从航迹8获得大矩阵，从中依次挑出一列作为测试样本v，统计1 080个测试样本的分类正确率。

按照2.3节的NMF+SRC流程进行处理。本文的关注点为不同降维方法结合SRC的分类正确率，所以在步骤4根据x进行分类时选用了最简单的策略，即由x中最大系数值的位置所处的区间指示目标类别。比如C的前1/3列来自轿车目标的训练样本，给出一个测试样本，经“降维+SRC”处理后若x中最大系数值位于x的前1/3位置，则正确识别。

3.2方法对比

实验对比了文献［2］所采用的几种典型“降维+ SRC”方法，各方法的区别概述如下∶

（1）降采样+稀疏表示分类（Down-Sampling+ SRC）

Down-Sampling后文简称为DS。将训练样本图像、测试样本图像均匀降采样，使每幅图像的尺寸由30 pixel×40 pixel变为6 pixel×8 pixel。由降采样后的训练样本图像拉直后构造CDS，降采样后的测试样本图像拉直作为cDS。

（2）随机投影+稀疏表示分类（Random+SRC）

对M左乘随机投影矩阵R48×1200，以此获得Crand，R的元素服从N（0，1）高斯分布。对拉直后的测试样本图像v左乘同样的随机投影矩阵R，获得低维数的crand。

（3）主成分分析+稀疏表示分类（Eigen+SRC）

需要说明的是，为了与文献［2］一致，用Eigen一词而未用PCA。M的各列减去均值列向量得到M0，对M0进行主成分分析，得到尺寸为1 200 pixel ×48 pixel的特征矩阵Feig，其每一列为一幅拉直的Eigen特征图像。基于Feig求取SRC所采用的字典Ceig与观测向量ceig如下∶

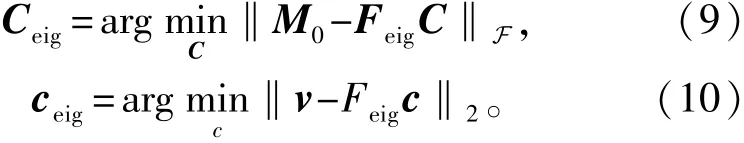
在稀疏表示分类环节，实验还对比了SRC（公式（8））与文献［6］所采用NSRC（公式（11））的性能差异。公式（11）通过将0范数凸松弛为1范数求

解［13］∶

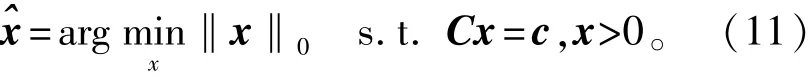
3.3实验结果

将测试样本加入不同程度的噪声，统计不同信噪比（SNR）级别时上述4种降维方法结合两种稀疏表示方法的识别率，结果如图5所示，可以得到以下结论∶

（1）各方法的分类正确率均随着SNR的提高而上升；

（2）采用NMF降维取得的分类正确率优于其他几种降维方法，不论稀疏表示环节采用标准SRC还是NSRC；SNR高于0 dB时，NMF+SRC的分类正确率超过95%，NMF+NSRC的正确率超过90%；

（3）对于每一种降维方法，与之配合的SRC取得的分类正确率都高于NSRC，以降采样配合NSRC（DS+NSRC）甚至失效。

图5　不同信噪比条件下分类正确率Fig.5 Success ratio of classification under various SNR conditions

对于第二个结论可以作如下解释∶SAR图像由散射中心构成，局部特征明显，适于用NMF获得的局部特征来描述。在提取出特征矩阵F后，训练样本和测试样本都可以仅用低维数的编码（图1中系数）有效地表示。将数据降到同样低的维数时，采用NMF得到的编码矩阵C与编码向量c分别比其他降维方法更好地描述了原始分辨率的训练样本与测试样本。因此在后续以C为字典对c进行稀疏表示时，NMF+（N）SRC获得了更高的分类正确率。

对于第三个结论，这里通过SRC与NSRC分别得到的稀疏表示系数的形态进行解释。图6与图7分别给出了一例典型测试样本采用SRC得到的稀疏表示系数与采用NSRC得到的非负稀疏表示系数。可以看到SRC在目标实际序号位置（训练样本序号730）具有突出的归一化系数值，容易形成正确判决，而NSRC只在采用NMF降维时能够很好地指示出目标。采用主成分分析降维时，NSRC给出的非负稀疏表示系数在非目标序号处也出现了大量突出值，值过大时可能造成错误判决。对于本例测试样本，采用降采样、随机投影降维配合NSRC得到的非负稀疏表示系数全为0，无法指示目标的类别，由此可见对稀疏表示系数进行非负约束会导致无法给出可行的稀疏解。这是因为缺少了负系数值的调节作用，算法无法仅用稀疏的正系数来近似表示出观测向量。

图6　采用标准SRC得到的稀疏表示系数Fig.6 Sparse representation coefficients with standard SRC adopted

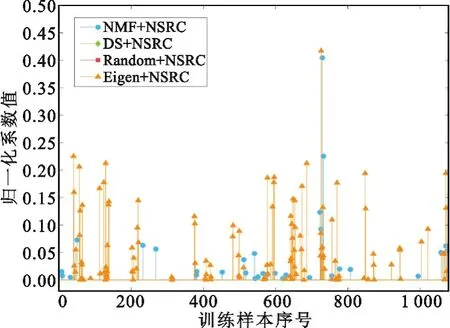
图7　采用NSRC得到的非负稀疏表示系数Fig.7 Non-negative sparse representation coefficients with NSRC adopted

4　结束语

本文提出了以非负矩阵分解提取局部特征的SAR目标稀疏表示分类方法（NMF+SRC），该方法利用SAR图像局部散射明显的特点，提取出局部特征编码用于稀疏表示分类。采用Gotcha项目SAR图像进行了车辆目标分类实验，结果表明与现有的采用降采样、随机投影、主成分分析提取特征的稀疏表示分类方法相比，NMF+SRC在不同信噪比条件下均取得了更高的分类正确率。本文方法是人脸识别领域稀疏表示分类方法在SAR领域的延伸，为SAR目标分类提供了新的途径。本文还对比分析了对稀疏表示系数进行非负约束与否对分类性能的影响，结果显示非负约束的稀疏表示导致分类正确率下降，故针对分类问题不宜在稀疏表示时进行非负约束。

［1］ ELAD M.Sparse and redundant representations［M］. New York∶Springer-Verlag，2010.

［2］ WRIGHT J，YANG A Y，GANESH A，et al.Robust face recognition via sparse representation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2009，31（2）∶210-227.

［3］ THIAGARAJAN Y J，RAMAMURTHY K N，KNEE P，et al.Sparse representations for automatic target classification in SAR image［C］//Proceedings of 4th International Symposium on Communications，Control and Signal Processing（ISCCSP）.Limassol，Cyprus∶IEEE，2010∶1-4.

［4］ XING X W，JI K F，ZOU H X，et al.Sparse representation based SAR vehicle recognition along with aspect angle［J］.The Scientific World Journal，2014（3）∶1-10.

［5］ XING X，JI K，ZOU H，et al.Ship classification in Terra-SAR-X images with feature space based sparse representation［J］.IEEE Geoscience and Remote Sensing Letters，2013，10（6）∶1562-1566.

［6］ 丁军，刘宏伟，王英华.基于非负稀疏表示的SAR图像目标识别方法［J］.电子与信息学报，2014，36（9）∶2194-2200.

DING Jun，LIU Hongwei，WANG Yinghua.SAR image target recognition based on non-negative sparse representation［J］.Journal of Electronics&Information Technology，2014，36（9）∶2194-2200.（in Chinese）

［7］ 龙泓琳，皮亦鸣，曹宗杰.基于非负矩阵分解的SAR图像目标识别［J］.电子学报，2010，38（6）∶1425-1429.

LONG Honglin，PI Yiming，CAO Zongjie.Non-negative matrix factorization for target recognition［J］.Acta Electronica Sinica，2010，38（6）∶2194-2200.（in Chinese）

［8］ 高馨，曹宗杰.基于稀疏约束的SAR目标特征提取方法研究［J］.雷达科学与技术，2013，10（6）∶618-623.

GAO Xin，CAO Zongjie.SAR target feature extraction based on sparse constraint nonnegative matrix factorization［J］.Radar Science and Technology，2013，10（6）∶618-623.（in Chinese）

［9］ LEE D D，SEUNG H S.Learning the parts of objects by non-negative matrix factorization［J］.Nature，1999，401（6755）∶788-791.

［10］ ASIF M S，ROMBERG J.Sparse recovery of streaming signals using-homotopy［J］.IEEE Transactions on Signal Processing，2014，62（16）∶4209-4223.

［11］ CASTEEL C H，GORHAM L A，MINARDI M J，et al.A challenge problem for 2D/3D imaging of targets from a volumetric data set in an urban environment［C］//Proceedings of SPIE 6568.Bellingham，WA∶SPIE，2007∶65680D-1.

［12］ 谢建志，张晓玲，田甲申，等.基于BP和CS相结合的圆周SAR三维成像算法［J］.电讯技术，2013，53（7）∶849-853.

XIE Jianzhi，ZHANG Xiaoling，TIAN Jiashen，et al.Threedimensional imaging algorithm for circular SAR based on combination of BP and CS［J］.Telecommunication Engineering，2013，53（7）∶849-853.（in Chinese）

［13］ YANG J，ZHANG Y.Alternating direction algorithms for ll_1-problems in compressive sensing［J］.SIAM Journal on Scientific Computing，2011，33（1）∶250-278.

张之光（1988—），男，江苏连云港人，2013年获工学硕士学位，现为博士研究生，主要研究方向为合成孔径雷达自动目标识别；

ZHANG Zhiguang was born in Lianyungang，Jiangsu Province，in 1988.He received the M.S.degree in 2013.He is currently working toward the Ph.D.degree.His research concerns synthetic aperture radar automatic target recognition.

Email∶diegozhangbit@163.com

雷 宏（1963—），男，研究员、博士生导师，主要研究方向为微波遥感系统技术、天线理论与工程。

LEI Hong was born in 1963.He is now a senior engineer of professor and also the Ph.D.supervisor.His research concerns microwave remote sensing system technology，antenna theory and engineering.

Sparse Representation Classification of SAR Targets with Local Features Extracted by Non-negative Matrix Factorization

ZHANG Zhiguang，LEI Hong
（Institute of Electronics，Chinese Academy of Sciences，Beijing 100190，China）

∶Synthetic aperture radar（SAR）target classification is one of the core functions in automatic targets recognition（ATR）system.It is essential in battle field surveillance，too.According to the characteristics that SAR images have prominent local scattering，it is proposed to perform non-negative matrix factorization（NMF）on the training samples to get low dimensional local encoding matrix，and subsequently perform sparse representation classification（SRC）based on this encoding matrix.Processing results on real data of civilian vehicle targets in Gotcha project demonstrate that the proposed method outperforms other dimension reduction methods such as down-sampling，random projection and principle components analysis，which are adopted with SRC.In this way，superiority of the method is revealed.Besides，the performances of SRC with and without non-negativity constraints are compared and analyzed by experiments.The experiment result reveals that SRC with non-negativity constraints leads to degradation of classification performance.In this way，it is unadvisable to include non-negativity constraint with regard to classification problem.

∶synthetic aperture radar（SAR）；sparse representation；targets classification；non-negative matrix factorization（NMF）；local feature extraction

TN959.1

A

1001-893X（2016）05-0495-06

10.3969/j.issn.1001-893x.2016.05.005

张之光，雷宏.以非负矩阵分解提取局部特征的SAR目标稀疏表示分类［J］.电讯技术，2016，56（5）∶495-500.［ZHANG Zhiguang，LEI Hong.Sparse representation classification of SAR targets with local features extracted by non-negative matrix factorization［J］.Telecommunication Engineering，2016，56（5）∶495-500.］

2016-02-02；

2016-04-20Received date：2016-02-02；Revised date：2012-04-20

**通信作者：diegozhangbit@163.comCorresponding author：diegozhangbit@163.com